<< Home
<< andere Mechanik-Beiträge
↓↓ Ende
Der Kraftbegriff bei A.Recknagel
in seinem Lehrbuch Physik − Mechanik (Verlag Technik Berlin, 1955)
Inhalt
Die Nummerierung 2. bis 5. folgt der im besprochenen Lehrbuch vorgenommenen Kapitel-Nummerierung.
Einleitung2. Dynamik der Punktmasse
3. Systeme von Punktmassen
4. Mechanik starrer Körper
5. Bewegung im beschleunigten Bezugssystem
Fazit
Verweise
Nachtrag: Die Corioliskraft (Dez.2019)
Einleitung
Für das Verständnis des Kraftbegriffs in der Physik/Mechanik [1] kann das im Titel genannte Lehrbuch von Alfred Recknagel, dessen Vorlesungen und Übungen ich in den 1950er-Jahren besuchte, empfohlen werden. Zur Erleichterung des Studiums habe ich ein diesbezügliches Exzerpt der Kapitel 2. bis 5. dieses Buches erstellt. Wörtliche Zitate sind fett und kursiv geschrieben. Von den Kapiteln 5. habe ich der Einfacheit halber ein paar wenige Seiten als Kopien beigefügt (erkennbar daran, dass nur etwa zwei Drittel der Seitenbreite belegt und der Hintergrund getönt ist). Meistens zitiere ich aber lediglich sinngemäß. Eingefügt sind Anmerkungen darüber, was sich zwischen den Zeilen geschrieben vermuten lässt und zu dem, was mir gelegentlich selbst durch den Kopf ging.
2. Dynamik der Punktmasse
"2. Dynamik der Punktmasse" (dynamis ist das altgiechische Wort für Kraft) folgt dem Kapitel "1. Kinematik" (kinema bedeutet Bewegung). Die Verallgemeinerung und der Übergang auf die praktisch immer vorliegenden komlexen Körper werden später im Kapitel "3. Systeme von Punktmassen" erfolgen. In der Dynamik wird nach den Ursachen der Bewegungen gefragt und in den Kräften gefunden.
2.01 Grundlagen des Kraftbegriffs
In den Grundzügen wird in der Physik das gleiche wie im Alltag verstanden. Sie haben dynamische (Wagen anschieben, Stein werfen) und statische (Feder gespannt halten) Wirkungen, und es kommt ihnen je eine Richtung zu.
Zwei gleich große, aber in entgegengesetzter Richtung wirkende Kräfte heben sich auf. Über ihre Größe können wir Genaueres als über unser Muskelgefühl nur durch Messung aussagen. Dafür wird irgend eine Kraftwirkung benutzt.
2.02 Das Trägheitsgesetz
Es wurde schon von GALILEI (1564 bis 1642) gefunden, sein Inhalt ist: Ein Körper beharrt in Ruhe oder in gleichförmiger geradliniger Bewegung, wenn keine Kraft auf ihn wirkt.
Seine mindestens qualitative Richtigkeit bestätigen die täglichen Erfahrungen: Beim Anfahren und Bremsen der Straßenbahn müssen wir uns festhalten, um auch beschleunigt zu werden und um nicht infolge der Trägheit unseres Körpers nach hinten oder nach vorne umzufallen. Der quantitative Beweis ist wegen der immer vorhandenen, wenn auch sehr klein haltbaren Reibung in irdischer Umgebung nicht möglich: Eine rollende Kugel wird über kurz oder lang zum Stillstand kommen.
Galilei war ein außerordentlich mutiger Wissenschaftler, indem er das Trägheitsgesetz, das nicht unmittelbar prüfbar ist, zur Grundlage der Mechanik machte.
[Das Trägheitsgesetz wurde zwar ein Forscherleben später von NEWTON (1643 bis 1727) indirekt durch die Anwendung auf die Planeten der Erde bestätigt. Die direkte Bestätigung, die Astronauten im All erfuhren, gab es noch nicht, als Recknagel sein Lehrbuch verfasste(1955).]
Nur die gleich schnelle geradlinige Bewegung benötigt keine Kraft. Jede andere Bewegung ist beschleunigt, und dann ist immer [permanent] eine Kraft die Ursache, und umgekehrt: Wenn eine Kraft wirkt, dann bewegt sich der Körper beschleunigt. Oftmals üben wir Kräfte auf Körper aus, ohne sie zu bewegen. Dabei ist aber immer wenigstens eine andere Kraft vorhanden, die sich mit unserer im Gleichgewicht befindet. Wir halten z.B. ein Gewichtstück mit ausgestrecktem Arm. Dabei wird unsere Hochhalte-Kraft von der Gewichtskraft (Schwerkraft) kompensiert.
2.03 Das Gegenwirkungsprinzip
Wird auf einen Körper aus seiner Umgebung heraus eine Kraft ausgeübt, so wirkt er auch auf die Umgebung zurück mit einer Kraft, die den gleichen Betrag, aber die entgegengesetzte Richtung hat.
Kraft = Gegenkraft Actio = reactio
Anmerkung: R. erwähnt nicht, dass es sich um das 3. Axiom von Newton handelt, aus dem andere Lehrbücher
und Publikationen u. a. folgern, was "echte Kräfte bzw. Kräfte im Sinne Newtons" seien, und dass Trägheitskräfte
nicht dazu gehörten und als "Scheinkräfte" behandelt werden müssten. R. meidet es, auf diese oder andere
Weise den praktischen Umgang mit dem Begriff Kraft zu erschweren. Das Wort "Scheinkraft" kommt bei ihm
überhaupt nicht vor. In einer der oben genannten Publikationen wird das Kind mit dem Bade ausgeschüttet: In jedem Falle sollte man
im Unterricht die Behandlung der Zentrifugalkraft (eine der Trägheitskräfte alias "Scheinkräfte") vermeiden, d.h. sich auf die Behandlung
der Zentripetalkraft beschränken [2, letzter Absatz].
R. führt mehrere Beispiele an, aber wie die anderen Publikationen leider auch keines, bei dem an der
Gegenwirkung ein beschleunigter Körper beteiligt ist.
Es kann gleichgültig sein, was actio und was reactio ist. Es gibt aber auch Fälle, in denen explizit zwischen eingeprägter Kraft und Zwangskraft zu unterscheiden ist (z.B. Gewicht|einprägend|actio steht auf Tisch|Zwang|reactio).
2.04 Statische Definition der Kraft, Kraftmesser
Annahme: Die Gewichtskraft eines Eich-Körpers kann als Bezugsgröße benutzt werden.
Definition: Das Gewicht ist der Menge der Materie proportional.
Kraftmessung: 1. Vergleich der unbekannten Kraft mit der bekannten Menge einer Masse bzw. deren Gewichtskraft
2. Dehnung einer geeichten Feder (Federdynamometer)
Anmerkung: Man lese Festlegung einer Bezugskraft anstatt Statische Definition der Kraft.
R. definiert die Kraft nur indirekt, indem er z.B. das Gewicht (die Gewichtskraft) definiert (s. auch 2.06.).
2.05 Das Kräfteparallelogramm
Kräfte sind Vektorgößen, d.h., sie werden nach dem Parallelogrammsatz zusammengefügt und zerlegt.
Anmerkung: Die gedachte Konzentration in einem Vektorpfeil versagt nur, wenn Krafteinleitungen in Körper zu
untersuchen sind.
2.06 Das Grundgesetz der Mechanik
Trägheitsgesetz (2.02). ohne Kraft keine Bewegungsänderung.
Grundgesetz: Kraft und Beschleunigung sind einander proportional: P = m · b (Newtonsche Grundgleichung).
Das NEWTONsche Grundgesetz definiert die Masse als Proportionalitätsfaktor zwischen beiden.
Anmerkung: R. erwähnt Newton hier zum ersten mal. In anderen Lehrbüchern muss Newton früher erscheinen,
um die Kraft durch den üblichen und meistens ausschließlichen Bezug auf das 2. Newtonsche Axiom als Ursache
einer Beschleunigung definieren zu können, beispielsweise so:
Eine Kraft ruft stets eine Beschleunigung hervor, sofern keine Gegenkraft wirkt [3]. Die Klarheit dieser Definition ist
aber wegen des Nebensatzes und des Nichteingehens auf die Trägheitskräfte (s. 2.03 und 5.02) geschmälert.
R. gibt bemerkenswerterweise keine direkte Definition für die Kraft, sondern lediglich Definitionen für das
Verständnis der Kraft hilfreicher Proportionalitäten (s.a. 2.04) an.
2.07 Maßeinheiten der Masse und der Kraft
R. benutzt in seinem Buch die zu seiner Zeit noch in der Technik gängige Kraft-Eiheit Kilopond. Das Newton erwähnt er: Die Kraft 1 Newton erteilt der Masse 1 kg die Beschleunigung 1 m·s-2.
Die Masse-Einheit 1 kg hat der in Paris als Urkilogramm aufbewahrte Platin-Iridium-Zylinder.
Anmerkung: Das Urkilogramm hat erst seit 2019 ausgedient.
2.08 Die Bedeutung der NEWTONschen Grundgleichung
Mit grundlegender Definition der Beschleunigung (hier nicht behandelt, siehe früher unter 1.11 Die Beschleunigung)
lautet die Grundgleichung
Px = m (dvx / dt) und Px = m (d2x / dt2) (Bewegung erfolge auf x-Achse)
Diese Formeln stellen den Zusammenhang zwischen der wirkenden Kraft und dem Ablauf der Bewegung her, was von besonderem Wert ist. Man spricht
von der Bewegungsgleichung der Masse.
2.10 Unabhängigkeit der Bewegungen
Wirken mehrere Kräfte an einem Körper, dann ist ihr Einfluß gleich denjenigen ihrer Vektorsumme; das Gesetz vom Kräfteparallelogramm gilt also auch für die dynamischen Wirkungen.
Mann kann die Kräfte in 3 Richtungen (z.B. in x-, y- u. z-Richtung) zusammenfassen und auf diese Weise die allgemeine krummlinige Bewegung darstellen.
2.11 Die NEWTONsche Grundlegung der Mechanik
NEWTONs "Mathematisierung" der Mechanik = außerordentliche Leistung.
R.-eigene Aufzählung der Newtonschen Axiome:
Gegenwirkungsprinzip (s.a. 2.03),
Satz vom Kräfteparallogramm (s.a. 2.05),
Trägheitsgesetz (s.a. 2.02),
Bewegungsgleichung (s.a. 2.08).
Ausnützen der Newtonschen Axiome:
a) Kräfte >>> Bewegungen - mathematisch eher schwierig
b) Bewegungen >>> Kräfte - mathematisch einfacher
2.13 Zwangskräfte
(Punkt-)Masse wird gezwungen, vorgeschriebenen Weg unter eingeprägten Kräften (s. 2.03) zu nehmen.
einfach: in Ebene bleiben (z.B. auf schiefer Ebene); streng: auf Bahn bleiben (z.B. im Gleis)
Zwangskräfte stehen immer senkrecht auf der erzwingenden Ebene/Bahn.
2.15 Die gleichförmige Kreisbewegung
Radialkraft R erzeugt Radialbeschleunigung a R = m· ω2· r a = ω2· r
2.18 Die Massenanziehung
Die Massenanziehungskraft zwischen zwei (Punkt-)Massen ist dem Produkt der beiden Massen proportional und umgekehrt proportional dem Quadrat ihres Abstandes. P = γ·m1·m2 / r2 .
3. Systeme von Punktmassen
Die Punktmassen sind nicht voneinander unabhängig, sondern stehen in Wechselwirkung/Gegenwirkung (2.03). Im Grenzfall bilden sie einen starren Körper (s.a. 4.). Die Pumktmassen sind inneren Kräften (Wechselwirkung) und äußeren Kräften unterworfen.
3.01 Der Impulssatz
Satz von der Erhaltung des Impulses = Impulssatz: Die Summe der Impulse eines Systems ist konstant, falls nur innere Kräfte wirken.
3.02 Der Massenmittelpunkt
Wirken nur innere Kräfte, so bewegt sich der Massenmittelpunkt mit konstanter Geschwindigkeit auf gerader Linie; für ihn gilt das Trägheitsgesetz. (2.02)
3.05 Die Wirkung äußerer Kräfte
Der Massenmittelpunkt bewegt sich so, als ob in ihm die gesamte Masse vereinigt sei und als ob an ihm die Summe aller äußeren Kräfte wirke.
4. Mechanik starrer Körper
Das Verhalten starrer Körper folgt Gesetzen, die einerseits wesentlich über die Punktmechanik hinausgehen, die andererseits aber nicht unnötig kompliziert sind.
4.01 Übergang von der Punktmasse zum starren Körper
Der Massenmittelpunkt eines starren Körpers bewegt sich so, als ob an ihm die Summe der äußeren Kräfte angreift. (s.a. 3.05)
5. Bewegung im beschleunigten Bezugssystem
Vorbemerkung:
Es handelt sich um das wichtigste Kapitel für Recknagels Kraftbegriff inklusive dem der Trägheitskraft.
Die 10 ersten, bis zur Zentrifugalkraft reichenden Buchseiten dieses Kapitels können in einer Original-Kopie
eingesehen werden: ReckBuchA.pdf.
Ich werde im Folgenden auch ein paar kopierte Textstellen einfügen um mir das aufwändige Abschreiben
- insbesondere von Gleichungen - zu ersparen.
Ein ruhendes Koordinaten- (bzw. Bezugs-) Sytem ist nicht immer zweckmäßig. Beispielsweise beschreiben die Füße eines Radfahrers von der Erde aus gesehen Schlangenlinien, während der Radfahrer selbst seine Füße sich einfach bewegend, nämlich rotierend sieht.
In vielen Fällen ist das bewegte Bezugssystem überhaupt das naturgegebene. Dazu gehört genau genommen auch die Erde, vor allem deshalb, weil sie sich um sich selbst dreht. Ihre Verwendung als ruhendes System ist zweckmäßig, aber fehlerbehaftet. Grundsätzlich erhebt sich die Frage, wie die Bewegung eines Körpers unter dem Einfluß gegebener Kräfte von einem bewegten Bezugssystem aus richtig zu beschreiben ist.
Recknagels Vorgehen:
Zuerst (5.01) wird gezeigt, dass kein Fehler beim Übergang von einem ruhenden in ein gleichförmig bewegtes
Bezugssystem entsteht.
Anschließend (5.02 und 5.03) werden die Änderungen erarbeitet, die für die richtige Beschreibung der
Körperbewegung von einem beschleunigten Bezugssystem (geradlinig beschleunigt bzw. gleichförmig rotierend)
aus erforderlich sind.
Die grundlegende NEWTONsche Bewegungsgleichung Masse mal Beschleunigung gleich Kraft (s. 2., insbes. 2.06) muß bereits bei ihrer Anwendung auf der Erdoberfläche genauer beleuchtet werden. Sie gilt in Strenge nur mit einer Kraft, die auch Bestandteile enthält, die von der Eigenbewegung der Erde (vorwiegend Eigendrehung) herrühren.
Folglich gilt die Bewegungsgleichung ohne solche Bestandteile nur im ruhenden Fixsternhimmel. Das entsprechende Bezugssystem ist in dessem Massemittelpunkt verankert und heißt Inertialsystem. Inertia = Trägheit: Damit wird darauf hingewiesen, dass in diesem System das Trägheitsgesetz (s. 2.02: ohne Kraft keine Beschleunigung ist "purer" Sonderfall der Bewegungsgleichung) gilt.
Relativitätsprinzip der NEWTONschen Mechanik: Jedes System, das sich gegen ein Inertialsystem gleichförmig geradlinig bewegt, ist ebenfalls ein Inertialsystem.
Anmerkung: Das Relativitätsprinzip der klassischen Mechanik wurde bereits von GALILEI angebgeben.
Der Beweis für dieses Gesetz wird mittels Koordinatentransformation durchgeführt. Diese wird anschließend variiert, d.h. zwischen einem Inertialsystem und beschleunigten Systemen vorgenommen und dabei die Trägheitskraft als der gesuchte Kraft-Bestandteil gefunden.
Koordinatentransformation:
5.02 Geradlinig beschleunigtes Bezugssystem
Das im Bild 177. durch Striche gekennzeichnete Koordinatensystem bewegt sich jetzt beschleunigt gegen ein Inertialsystem in Richtung der x-Achse. Für einen bewegten Körper werden von beiden Systemen aus unterschiedliche Beschleunigungen gemessen. In den Beziehungen (5.4) verschwindet das die Beschleunigung angebende Glied
d2x0 / dt2 nämlich nicht, und aus (5.8) wird
r' ist der Ortsvektor im beschleunigten System.
Ist ein Bezugssystem gegen ein Inertialsytem geradlinig beschleunigt, so ist das in ihm gemessene Produkt aus Masse und Beschleunigung gleich der Summe aus eingeprägter Kraft (P, s. 2.03) und Trägheitskraft (PT).
Anmerkung: R. stellt hier das D'ALEMBERTsche Prinzip dar, ohne es bei diesem Namen zu nennen.
Er vermerkt, dass die Trägheitskraft nichts als die Trägheit berücksichtige, unterlässt es aber, sie als "Scheinkraft,
unechte Kraft" o.ä. zu bezeichnen.
Einzel-Anmerkungen:
1. Wir nennen PT Trägheitskraft, weil sie nämlich nichts anderes berücksichtigt als die Trägheit.
M.E. ist die Trägheitskraft genau die Gegenwirkung/Wechselwirkung zu derjenigen eingeprägten Kraft, die den
trägen Körper beschleunigt, und das dritte NEWTONsche Axiom erweist sich als anwendbar:
Auf den beschleunigten Körper wird aus seiner Umgebung heraus eine Kraft ausgeübt, und dieser wirkt auf
die Umgebung zurück mit einer Kraft, die den gleichen Betrag, aber die entgegengesetzte Richtung hat (s. 2.03).
Das Wirkungspaar actio/reactio heißt in diesem Falle eingeprägte/Trägheits- Kraft. Hiermit stelle ich mich gegen
Aussagen, wie diese [2, Seite 24, 2. Absatz links]:
Zu [den] Trägheitskräften gibt es .. keinen Wechselwirkungspartner, also keinen zweiten Körper, der eine solche
Kraft auf den beschleunigten [Körper] ausübt und auf den selbst die betragsgleiche Kraft ausgeübt wird. Da eine
Trägheitskraft keine Kraft im Sinne der Newtonschen Axiome ist, wird sie als Scheinkraft bezeichnet
M.E. gehört die Trägheitskraft in die Newtonschen Axiome, und sie gibt es auch in einem Inertialsystem
(was i.d.R.in ähnlichen Aussagen verneint wird).
2. Dies wird klar, wenn in (5.9') die eingeprägten Kräfte verschwinden. ...
Das Beobachter-Koordinatensystem ist mit dem zu Px passenden Wert b0 beschleunigt bewegt.
Bei verschwundenem Px macht die Masse diese Bewegung nicht mit und ruht nicht im Beobachtersystem,
sondern bewegt sich mit − b0, also in entgegengesetzter Richtung. Die gemäß NEWTONscher Bewegungs-
gleichung dafür erforderliche Kraft hat den Wert m·(−b0x) = − m·b0x, und wird Trägheitskraft genannt.
Die eingeprägte Kraft Px ist nicht verschwunden, R. hat sie nur ausgeblendet bzw. ihr eine andere Aufgabe
zugeteilt, nämlich die Trägheitskraft PTx auszugleichen, so dass die Masse im Beobachter-Koordinatensystem ruht.
Es besteht Gleichgewicht zwischen Px = + m·b0x und PT = − m·b0x , das im von R. nicht erwähnten
d'ALEMBERTschen Prinzip als dynamisches Gleichgewicht bezeichnet wird.
Die NEWTONsche Bewegungsgleichung nicht in einem Inertial- sondern in einem gegen dieses beschleunigt
bewegten Koordinatensystem anzuwenden - wie eben gemacht - ist also wenigstens formal möglich. Das
beschleunigt bewegte System wird zum unbewegten System, gegen das sich das vorher Inertialsystem gewesene
entgegen der vorherigen Richtung bewegt. Wenn im ursprünglichen Inertialsystem keine eingeprägte Kraft auf eine
Masse wirkt, so bleibt diese in Ruhe. Der jetzt unbewegte Beobachter sieht, dass sich diese Masse in seinem
System gemäß Bewegungsgleichung durch Wirkung einer Kraft rückwärts bewegt. Er erkennt, dass diese Kraft
dengleichen Wert |m·b| hat, wie eine im ursprünglichen Inertialsystem wirkende, die der Masse diegleiche
Beschleunigung erteilt, wie sein Beobachter-System ursprünglich hatte.
Das Gesagte lässt sich mittels dreier Umkehrungen (1., 2. und 3.U) verkürzt formulieren:
Beobachtung im Inertialsystem:
Masse in Ruhe (1.U), wenn keine Kraftwirkung (2.U); ein anderes System werde mit b0; beschleunigt (3.U).
Beobachtung im mit b0 beschleunigten Koordinatensystem:
Masse in beschleunigter Bewegg. (1.U) infolge einer Kraftwirkung (2.U); Beschleunigg. der Masse mit −b0 (3.U).
3. ... gleich der Summe aus eingeprägter Kraft und Trägheitskraft
Dass im Inertialsystem Trägheitskraft oder ein anderer Name für den zweiten Part der Wechselwirkung in den
NEWTON'schen Axiomen oder in deren Interprätationen gar nicht vorkommt, erstaunt mich. Lautet doch die
Definition für Kraft, dass diese einen Körper gegen dessen innewohnende Trägheit beschleunigen kann.
Dass dieser Körper im beschleunigten Bezugssystem ruhen muss, ist hingegen evident. Er ist selbst der
Gegenstand, auf den bezogen werden soll, und das Koordinatensystem ist als Mittel zum Zweck an ihn angeheftet.
Auf den im beschleunigten Bezugssystem ruhenden Körper wirkt keine (resultierende) Kraft, bzw. es herrscht
Gleichgewicht zwischen der eingeprägten Kraft und dem zusätzlichen Kraftanteil (s. 5.01).
Weil der Wechselwirkungspartner zur eingeprägten Kraft Trägheitskraft heißt, ist diese mit dem zusätzlichen
Kraftanteil identisch.
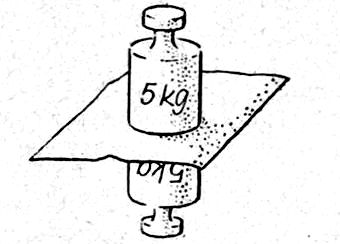Anschauliches Experiment: Bild 178. − gegenseitige Kraft zweier fallender Körper:
Der mitfallende Beobachter kann das Papier leicht wegziehen, denn an beiden Gewichten wird die nach unten ziehende Gewichtskraft m·g von der nach oben wirkenden Trägheitskraft m· (d2z/dt2) gerade ausgeglichen.
Der ruhende Beobachter konstatiert, dass beide Gewichte frei fallen, also derselben Erdbeschleunigung g unterliegen.
(Übrigens: Die beiden Gewichte müssen nicht gleich groß sein.)
5.03 Die Zentrifrugalkraft (rotierend beschleunigtes System)
Die Zentrifugalkraft ist eine Trägheitskraft, die in einem rotierenden Bezugssystem eingeführt werden musss, wenn das Trägheitsgesetz gelten soll. Für Körper, die in einem rotierenden Bez.system ruhen, verschwindet die Summe aus eingeprägter Kraft und radial nach außen zeigender Zentrifugalkraft.
eingeprägte Radialkraft Pr = − m·ω2·r gleich m·ω2·r = Pz Zentrifugalkraft
Anmerkung: Man lese weil sonst das Trägheitsgesetz nicht anwendbar wäre anstatt wenn das Trägheitsgesetz
gelten soll, denn wir ziehen das wollen dem sollen vor.
Meine allgemeinen Gedanken (s. 5.02: Einzel-Anmerkungen) gelten selbstverständlich auch für diese besondere
beschleunigte Bewegungsart. Die eingeprägte Kraft hat hier den besonderen Namen Radial- oder Zentripetal-
kraft, und die Trägheitskraft heißt hier Zentrifugal- oder Fliehkraft.
In diesem Leitfaden der Physik wird von Zentrifugalkraft nur im Zusammenhang mit rotierende Bezugssystemen gesprochen. Der Stundent macht also sicher keinen Fehler, wenn er erst klar sagt, daß der Vorgang von einem rotierenden Bezugssystem aus betrachtget werden soll, bevor er das Wort Zentrifugalkraft anwendet.
Anmerkung: R. gibt diesen dringlichen Rat, um den sicheren Umgang mit der Zentrifugalkraft und anderen
Trägheitskräften zu fördern. Moderne Physik-Didaktiker befleißigen sich stattdessen des Unworts Scheinkraft
bzw. empfehlen,die Zentrifugalkraft im einführenden Physik-Unterricht nicht zu behandeln [2, letzter Absatz].
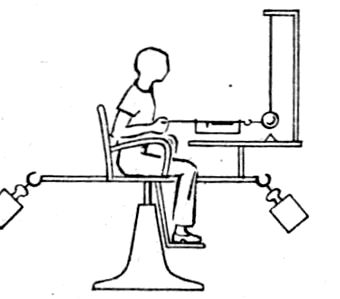Anschauliches Experiment:
Bild 182. − Beobachtung der Zentrifugalkraft:
Der mitrotierende Beobachter hält die Kugel mit einer von ihm erzeugten Zugkraft in Ruhe. Diese bleibt gemäß Trägheitsgesetz nur in Ruhe, wenn eine radial entgegengesetzte Kraft (die Zentrifugalkraft) die Zugkraft ausgleicht.
Der ruhende Beobachter konstatiert, dass der mitrotierende Beobachter die für die Kreisfahrt der Kugel erforderliche Radialkraft aufbringt.
(Übrigens: Der mitrotierende Beobachter sitzt mit seinem Schwerpunkt nur deshalb etwa in der Drehachse des Drehstuhls, um ihn möglichst nicht auch einer Zentrifugalkraft zu unterwerfen.)
Anmerkung: Im Versuch wird das Trägheitsgesetz für den Grenzfall bestätigt, dass die Geschwindigkeit Null eines
Körpers ohne Krafteinwirkung Null bleibt. Die Zentrifugalkraft tritt aber stets an den Köpern auf, gleichgültig, ob
sie im rotierenden System ruhen oder sich relativ zu diesem bewegen.
Die vom mitrotierenden Beobachter vorgenommene Messung der Radial-/Zentrifugalkraft und deren Auswertung
zur Null-Summe ist nur sinnvoll bzw. nur möglich, wenn er sich seiner Kreisfahrt bewusst ist und deren Daten
(ω und r) kennt. Der Kreisfahrt auf der sich drehenden Erde ist man sich i.d.R. nicht bewusst. Zudem ist es
schwerer als im obigen Experiment, sich die entsprechenden Daten zu beschaffen.
Anders gesagt: Der Physik-Anwender kann nach dem Wechsel in ein mitbeschleunigtes Bezugssystem das
Inertialsystem nicht "unbeachtet hinter sich lassen".
Fazit
Dem hinter dem Kraftbegriff steckenden physikalischen Phänomen Kraft ist in Kürze nicht nahe zu kommen. Das von mir erachtete Minimum seiner Beschreibung und Erwähnung in Recknagels Buch betrifft vier von acht Kapiteln. Außer im ersten kann in keinem Kapitel auf die Kraft verzichtet werden. Wegen dieser Stofffülle erwähne ich mehrere verzichtbare Begriffe aber nicht. Einige davon haben Kraft als Wortteil (Reibungs-, Corioliskraft [s. Anhang], Kraftstoß, Kräfte-Paar u.a.), andere sind ohne Kraft nicht definierbar (Druck, Spannung, mechanische Arbeit, Energie und Leistung u.a.).
Recknagels ältere Kollege R.W.POHL schreibt: Der Nutzen dieser Größe [Kraft] ist unbestreitbar. Trotzdem ist wohl kein physikalischer Begriff dunkler und rätselvoller als der der Kraft.[4] Ihm und auch Recknagel ist es dennoch gelungen, diesen Begriff selbst Lernenden, die die Physik nur anwenden (Techniker) oder als Allgemeinbildung erwerben, verständlich zu machen. Besonderen Anteil am Erfolg hatten die in den Vorlesungen vorgeführten Experimente.
Für Recknagel ist die Anwendung des D'ALEMBERTschen Prinzips (s. 5.02) selbstverständlich. Er erwähnt dessen Namen nicht, aber auch den NEWTONs nicht in einer Art, als würde die NEWTON'sche Mechanik selbst ein natürliches Phänomen sein. Den Verdacht auf eine solche Haltung habe ich bei den derzeitigen Physik-Didaktikern [2]. NEWTON hat in der Mechanik und in anderen Teilen der Physik-Wissenschaft sehr erfolgreich gearbeitet. Er beschrieb die natürlichen Phänomene, von der wir prinzipiell niemals genaue Kenntnis haben werden, erstmals in großen Teilen und sehr nützlich für unsere aktive Teilnahme an der Natur. Andere Wissenschaftler folgten ihm mit ebenfalls nützlichen Erkenntnissen, die aber nicht immer direkt an seine Axiome anschließen. Einer davon war D'ALEMBERT. Recknagel hat dessen Art der Beschreibung übernommen. Ernsthafte moderne Kritiker möchten die D'ALEMBERTsche Methode abschaffen, denn die Zentrifugalkraft z.B. ...verstellt ... das Verständnis für die Newton'sche Beschreibung der Bewegung." [2] An gleicher Stelle heißt es: "Ein wichtiges Ziel ist sicher das Verständnis der Newton'schen Axiome, was allerdings schlecht gelingt." Das an sich schwierige Ziel (s. obigen Satz von POHL) zu erreichen, wird nicht gefördert, indem die Axiome wie Dogmen oder Glaubenssätze behandelt werden. In besonderen Fällen nicht auf den fragwürdigen Bezug auf eines der Axiome (3. Axiom: "Zu .. [den] .. Trägheitskräften gibt es .. keinen Wechselwirkungspartner ..." [2, Seite 24, 2. Absatz links] ) verzichten zu können, ist dogmatischem Eifer geschuldetes Unvermögen.
Verweise
[1] Alfred Recknagel: Physik − Mechanik, Verlag Technik Berlin, 1955, geküzte Auszüge:
ReckBuchA.pdf (Seiten 236 - 45) und
ReckBuchA.pdf (Seiten 249 - 57.
Siegfried Wetzel: Über den Kraft-Begriff in der Mechanik
(Dieser Artikel ist eher als Stoffsammlung für die vorliegende Arbeit anzusehen, als dass er ausreichende
Antworten vorwegnimmt.)
Siegfried Wetzel: Coriolisbewegung
[2] Thomas Wilhelm: Trägheitskräfte im Mechanikunterricht? 2016
[3] Bergmann - Schäfer - Gobrecht: Lehrbuch der Experimentalphysik, Band I, de Gruyter, 1974
[4] Robert W. Pohl: Mechanik · Akustik und Wärmelehre, Göttingen, 1930
(Dieses Werk ist ähnlich aufgebaut wie das von Recknagel, dem es möglicherweise als Vorbild diente.)
[5] Richard P.Feynman u.a.: Feynman-Vorlesungen über Physik, Band 1, hauptsächlich Mechanik, Strahlung und
Wärme, R.Oldenbourg, 1977, Bilingua-Ausgabe (deutscher Text von Heinz Köhler), Kapitel 19−4, Seite 19−13.
Feynman erwähnt ebenfalls Recknagels Beispiel (Bild 190) und führt an, was der sich drehende Beobachter
"sieht". Darunter befindet sich auch die Zentripetalkraft (5.16), die mit "der Drehung nichts zu tun hat.". Das
dynamische Gleichgewicht und die damit verbundene Anwendung des Prinzips von D'ALEMBERT kommt leider
auch nicht zur Sprache.
Nachtrag: Die Corioliskraft (Dez.2019)
Die entsprechenden Buchseiten können in Original-Kopie eingesehen werden: ReckBuchB.pdf.Siehe auch meinen Artikel Coriolisbewegung
Die Corioliskraft ist eine weitere Trägheitskraft. Mit ihr hat man sich vorwiegend in den Geowissenschaften Ozeanographie und Meteorologie und weniger in der Ingenieur-Mechanik zu befassen.
5.05 Die CORIOLISkraftDie CORIOLISkraft ist eine Trägheitskraft, die im rotierenden Bezugssystem außer der Zentrifugalkraft eingeführt werden muß, wenn die NEWTONsche Grundgleichung in der üblichen Form gelten soll. Das Produkt aus Masse und Beschleinigung ist gleich der Summe von eingeprägter Kraft, Zentrifugalkraft und CORIOLISkraft.
Anmerkung: In 5.03 (Die Zentrifugalkraft) war R. nur deshalb nicht zum Hinweis, dass die Corioliskraft auch
einzuführen ist, genötigt, weil diese im Versuch (Bild 182) Null war (die Kugel wurde im rotierenden Bezugssystem
in Ruhe gehalten).
Die CORIOLISkraft wirkt nur an solchen Massen, die sich im drehenden System selbst bewegen. Sie steht senkrecht auf der Bahn und zeigt nach rechts, wenn sich das System, von oben gesehen, der Bewegung des Uhrzeigers entgegendreht. Sie zeigt nach links beim anderen Drehsinn.
Anmerkung: Weil die Massen auch in den meisten einschlägigen Anwendungen (Karussell u.a.) im System
ruhen, sei daran erinnert, dass die Zentrifugalkraft stets auftritt, gleichgültig, ob die Massen im rotierenden System
ruhen oder sich relativ zu diesem bewegen (5.03).
5.06 Berechnung der CORIOLISkraft
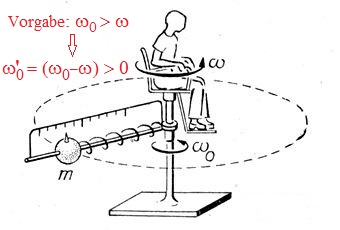Anschauliches Experiment: Bild 190. − zur Berechnung der CORIOLISkraft
Der mit ω rotierende Beobachter bildet das Bezugssystem. Die Masse m rotiert auf einem Kreis (Radius r , der sich gegen die Kraft einer Feder einstellt, r wählbar durch Verschieben deren Festpunkts)
mit ω0 im ruhenden System bzw.
mit ω'0 = ω0−ω ( 5.15) relativ zum Beobachter.
Anmerkung: Ich werde zugunsten der Lesbarkeit darauf verzichten, doppelte Vorzeichen in Gleichung (5.15) anzuwenden. Es ist selbstverständlich, dass das Ergebnis-Vorzeichen bei einer umgekehrten Vorzeichen-Vorgabe umkehrt ist.
Anmerkung: Im Original-Text gibt es die Schlussbemerkung:
Die CORIOLISkraft ist, ..., in diesem Beispiel radial gerichtet.
Anstatt ist radial gerichtet lese man Der Beispiel-Versuch wurde so gestaltet, dass die Corioliskraft radial gerichtet
ist.. Er solte unmittelbar an den Beispielversuch für die Zentrifugalkraft (5.03, Bild 182) anschließen: Beide
Trägheitskräfte haben die gleiche Richtung und können gemeinsam gemessen werden.
Nebenbemerkung: Eine Masse m in wiederkehrender Bewegung auf einer geschlossenen Kreisbahn läuft
nicht frühzeitig davon wie eine radial bewegte. Eine Versuchseinrichtung für die meistens beim Kennenlernen
des Corioliseffektes betrachtete radiale Bewegung ist prinzipiell möglich. Sie könnte sogar von der
Zentrifugalkraft unbeeinflusst sein, wenn sie zwangläufig mit der gleichmäßigen Rotation des Bezugssystems
erfolgt, wäre aber für sicheres Beobachten und Messen zu kurz. In einen Versuch (Bild 190) mit rotierender
Masse ist die kraftfreie Umlauf-Bewegung permanent, und die radial wirkende Corioliskraft ist leicht messbar.
Bei der Corioliskraft vermisse ich besonders, dass Recknagel seine Erklärungen nicht durch Betrachtung des Dynamisches Gleichgewichts (Prinzip von D'ALEMBERT) unterstützt. Hier handelt es sich nämlich um vier (bei der Zentrifugalkraft (5.03) nur um zwei) im gegenseitigen Gleichgewicht stehende Kräfte, deren physikalische Beziehungen untereinander in der von R. angestellten Berechnung der CORIOLISkraft nicht herausgestellt werden.
Ich lasse eine variierte Darstellung folgen, die zum Ergebnis neben der Berechnung der Corioliskraft (ein Ausdruck für die Corioliskraft) auch das Dynamische Kräftegleichgewicht (eine Gleichung mit Ausdrücken für einzelne Kräfte, deren Summe Null ist) hat.
Variierte Darstellung:
Die auf die Masse m eingeprägte Kraft ist Pr = − m·r·ω02 (5.14).
Gesucht ist das (dynamische) Kräftegleichgewicht zwischen eingeprägten und Trägheitskräften an der Masse m
im mit ω rotierenden Beobachtersystem. Wir drücken deshalb die Gleichung (5.14) mit ω0 = ω + ω'0 (5.15a)
als Funktion der Rotationsgeschwindigkeit ω (und der Relativgeschwindigkeit ω'0) aus:
Pr = − m·r·ω02 = − m·r·(ω + ω'0)2 = − m·r·ω2 − 2·m·r·ω·ω'0 − m·r·ω'02 .
Formalismus für das Aufstellen des dynamischen Kräftegleichgewichts:
Ich werde − der Not gehorchend und in guter Gesellschaft mit allen mir bekannten Physik-Lehrbüchern − das D'ALEMBERTsche Prinzip
nur formal anwenden und ebenfalls einen Bogen um den offensichtlich schwierigen Versuch machen, einen sauberen physikalischen
Kontext zu finden.
Man stellt die NEWTONsche Bewegungsgleichung (5.14) so um , dass auf einer Seite des Gleichheitszeichens
Null steht:
Pr + m·r·ω2 + 2·m·r·ω·ω'0 + m·r·ω'02 = 0 (5.14a)
und fasst die der eingeprägten Kraft Pr folgenden 3 Terme als ihr das Gleichgewicht haltende Kräfte auf.
Der erste der 3 Terme drückt die Zentrifugalkraft der mit ω rotierende Masse (im rotierenden Bezugssystem
ruhend) aus.
Der dritte Term ist Ausdruck für die Zentrifugalkraft der mit ω'0 relativ zum rotierenden System des Beobachters
rotierenden Masse. Sie ist d'Alembert-gemäß der Radialkraft Pr' (5.16) mit umgekehrten Vorzeichen gleich.
Pr' hat damit, dass sich das System dreht (ω), nichts zu tun, was hier [5] bestätigt wird.
Der zweite Term ist schließlich die Corioliskraft mit dem berechneten Ausdruck
PC = 2·m·r·ω·ω'0 = 2·m·ω·v' (5.18).
Pr + PZ + PC - P'r = 0
ist das mit kürzeren Formelzeichen geschriebene Dynamische Gleichgewicht. (5.14a) >> (5.19a) .
Anmerkung: Den unterlassenen Beweis vermisse ich nicht. Dass der Winkel zwischen den beiden
Bewegungsachsen mit dem Sinus seines Wertes eingeht, ist mir plausibel. Dass die Corioliskraft immer
rechtwinklig zu einer beliebigen Bewegungsrichtung der ihr unterworfenen Masse ist, braucht ebenfalls keine
vertiefte Untersuchungen. Dass die Corioliskraft vom Radius r nur indirekt abhängig ist, ergibt sich im Beispiel
durch Zusammenfassen von ω·r zu v' (v' ist zu r proportional). Die Antwort auf die Frage, warum die
Corioliskraft bei gleichförmiger Radialbewegung konstant ist und nicht mit r größer wird, fehlt.
5.07 CORIOLISkräfte auf der Erde
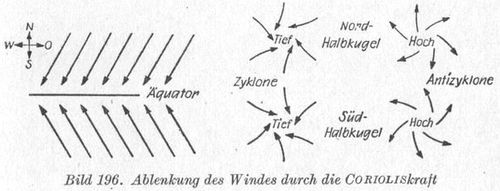
Anmerkung: Ich übernehme R.s Bild 196 als kurze Zusammenfassung über das Kapitel Corioliskraft.
Es enthält die häufig in Wetterberichten gezeigten (teilweise in Satelitenfotos) und leicht nachvollziehbaren
Folgen dieser Erscheinung.
Siegfried Wetzel, CH 3400 Burgdorf, November 2019 (Dez.19, Jan.20)
↑↑ Anfang
<< andere Mechanik-Beiträge
<< Home