<< Home
<< andere Sonnenuhren-Beiträge
 ↓↓ Ende

Analemmatische Sonnenuhr mit Peilpunkten
für Sonnenaufgang- und -untergang (Seasonal Markers)

Zusammenfassung

Roger Bailey beschrieb im Jahre 2003 sogenannte Seasonal Markers, die auf horizontalen analemmatischen Sonnenuhren [1] und [2] in mittleren geographischen Breiten angebracht sind [3]:

* einen Punkt, mittels dem man in die Richtung des Sonnenaufgangs am Horizont
  oder in Richtung seines Stundenpunkts auf der Skala peilen kann,
* und einen entsprechenden Punkt für den Sonnenuntergang.

Der für den Sonnenaufgang benutzte Peilpunkt liegt auf der westlichen Halbachse der Skalenellipse. Wenn man über ihn vom richtig eingestellten vertikalen Schattenstab aus peilt, so blickt man in guter Näherung auf denjenigen Punkt der elliptischen Stundenskala, der mit der Zeit des Sonnenaufgangs zu diesem Datum übereinstimmt. Blickt man vom Peilpunkt aus über den Schattenstab in die Gegenrichtung, so sieht man am Horizont den Punkt, an dem die Sonne zu diesem Datum aufgegangen ist.

Auf der östlichen Halbachse liegt der für den Sonnnenuntergang zu benutzende Peilpunkt.

Beim Peilen liegen drei Punkte auf einer geraden Linie. Der bei der analemmatischen Sonnenuhr bekannte Lambert'sche Kreis enthält fünf typische Punkte, die auf einer kreisförmigen Linie liegen. Dieser Kreis wird einleitend für Vergleiche mit der zu besprechenden Peilmethode betrachtet.

Inhalt

1.  Der Lambert'sche Kreis  ↑ Anfang

1.1  Johann Heinrich Lambert und der nach ihm benannte Kreis    ↑ Anfang

Der im 18. Jahrhundert lebende elsässische Mathematiker Johann Heinrich Lambert (Anmerkung 1) erkannte, dass ein Kreis durch die beiden Brennpunkte der Skalen-Ellipse und durch den Fußpunkt des Schattenstabes (Datumspunkt) auch die Skalenpunkte der Zeit des Sonnenauf- und des Sonnenuntergangs des entsprechenden Datums enthält.

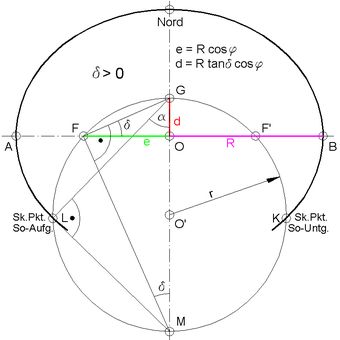<< Abb.1  Zifferblatt einer horizontalen analemmatischen
                Sonnenuhr mit zusätzlichem
                Lambert'schen Kreis; φ = 56°; δ = +23,45°
                [4: Abb.3, nachgezeichnet u. ergänzt]

Lambert hat diesen Kreis in die entsprechende Abbildung (Tab.3, Fig.1) seiner Veröffentlichung [0] nicht eingezeichnet. Der Begriff Lambert'scher Kreis wurde von einem Briefpartner von René Rohr geprägt, und die damit verbundene Erkenntnis fand erst durch eine Veröffentlichung Rohr's [4] wieder Beachtung. Lambert benennt den Nutzen dieses Kreises mit folgenden Worten:
"Da man aber, um diesen Circul zu ziehen, nur drey Puncte nöthig hat, so kann man die Puncte L, K bestimmen, wenn man den Circul durch F', G und F zieht.",
hält aber einen detaillierten Nachweis für die Richtigkeit "seines" Kreises für nicht erforderlich:
"Es ist unnötig, hier mit anzumerken, dass die Punkte L, F ,G , F' und K sämtlich im Umkreis eines Circulus liegen, weil dieses aus dem, dass GL und GK Normallinien sind, für sich folgt." [0: § 6]

Rohr hält das für eine "etwas unklare Mitteilung". Dem stimme ich zu, halte aber Rohr's längere "einfachere Betrachtungen" selbst in Teilen für ein unklares und in anderen Teilen für ein umständliches und auch nicht konsequentes Vorgehen, was wiederum mich anregte, eigene Betrachtungen anzustellen.

1.2  Rechnerische Untersuchung des Lambert'schen Kreises    ↑ Anfang

Ich versuche wie Rohr, mich der Lambert'sche Normalen/Tangentenaussage durch Rechnen zu nähern. Das heißt lediglich zu zeigen, dass der Lambert'sche Kreis auch die Skalenpunkte L unf K (Sonnenauf- und -untergang) enthält, wenn der Durchmesser eines anstatt mit den Punkten F, F' und G mit L, K und G ermittelter Kreises gleich groß ist.

Wegen der Symmetrie zwischen Vor- und Nachmittagsteil der Sonnenuhr liegt der Mittelpunkt des Lambert'schen Kreises auf der Süd-Nord-Geraden. Die Betrachtungen reduzieren sich einerseits auf einen der beiden Brennpunkte, andererseits auf einen der beiden Skalenpunkte. Angewendet wird der Satz des Thales: Der auf der Süd-Nord-Geraden liegende Durchmesser des untersuchten Kreises wird vom Punkt G begrenzt: Durchmesser 2r = GM. Ein Dreieck aus den beiden Endpunkten des Durchmessers und einem dritten Kreispunkt ist an letzterem rechtwinklig. Bekannt sind die Längen GF bzw. GL und deren mit dem Durchmesser gebildeter Winkel 90°-δ bzw. α. Mit diesen je zwei Bestimmungsstücken in den rechtwinkligen Dreiecken ist deren Hypotenuse - der gesuchte Durchmesser - in einfacher Weise darstellbar.

Durchmesser des die Brennpunkte F und F' enthaltenden Kreises durch G
R = große Halbachse der Ellipse
φ = geographische Breite des Aufstellortes der Sonnenuhr; δ = Deklinationswinkel der Sonne.
Die Länge von GF ist
    GF = R cosφ / cosδ     (GF = e / cosδ    e = - R cosφ, Anmerkung 2)
Im Dreieck MFG gilt:
    2r = GM = GF / sinδ     > >      2r = R cosφ / (cosδ sinδ) .                 Rohr's Vorgehen: siehe Anmerkung 3

Durchmesser des die Skalenpunktepunkte L und K enthaltenden Kreises durch G
Die Linie GL ist Teil des in der Zifferblattebene liegenden Streifschattens des Stabes bei Sonnenaufgang. Bei einer horizontalen analemmatischen Sonnenuhr ist sie (unabhängig von φ !) gleich lang wie die Mantellinie des Tages-Schattenkegels zwischen Nodus und entsprechendem äquatorialem Ring ([1 Bild 4], Anmerkung 4).
    GL = R / cosδ.
Das Azimut α des Streifschattens ist
     cosα = sinδ / cosφ   [6 Abb.6: Morgenweite ν, α=90°-ν].
Im Dreieck MLG gilt:
    2r = GM = GL / cosα     > >     2r = R cosφ / (cosδ sinδ) .                 Rohr's Vorgehen: siehe Anmerkung 5

Ergebnis der Untersuchung
Die beiden erhaltenen Darstellungen sind identisch gleich: Der Lambert'sche Kreis enthält sowohl die Brennpunkte der elliptischen Skala als auch die Skalenpunkte für die Zeitpunkte des Sonnenauf- und -untergangs.
Die Gleichheit beruht auf der oben postulierten besonderen Beziehung, die für die zwischen den Punkten L und F (und G) wie folgt lautet:
                                                  FG / cos (90°-δ) = LG / cos α .

Gleichung für den Radius des Lambert'schen Kreises
Unter Ausnutzung des Additionstheorems   cosδ sinδ = sin2δ / 2   wird aus der vorstehenden (zweimal abgeleiteten) Darstellung die Gleichung:             r = R cosφ / sin2δ .

Mit dem jetzt bekannten Radius des Lambert'schen Kreises ist eine Kontrollrechnung möglich, die zeigt, dass die Punkte auf der großen Ellipsenachse, in denen sich alle Lambert'schen Kreise (δ variabel, φ konstant) schneiden, die Brennpunkte sind (siehe Anmerkung 6).

1.3  Sonderfall des Lambert'schen Kreises: Gerade bei δ = 0°    ↑ Anfang

Bei Sonnendeklination δ = 0° ist der Lambert'sche Kreis eine Gerade (Abb.2: sein Durchmesser ist unendlich groß), auf der die Punkte L, F ,G , F' und K liegen. Folgerung: Sie liegen sämtlich auch dann auf dem Lambert'schen Kreis, wenn dieser im Allgemeinen einen endlich großem Durchmesser hat.

2.  Die Peil-Linien über die Seasonal Markers    ↑ Anfang

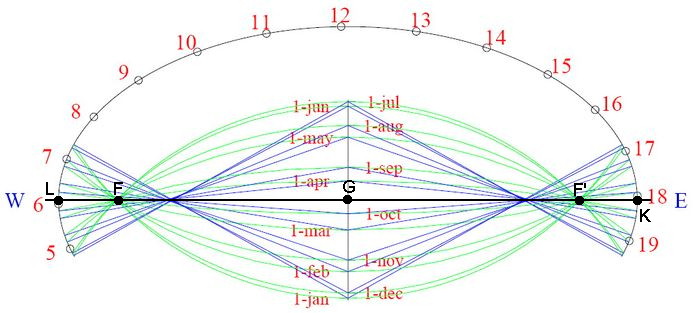Abb.2  Analemmatische Sonnenuhr für geographische Breite φ = 36,9° Nord mit
           grün: Lambert'sche Kreise (-23,5° ≥ δ ≥ +23,5°, gemeinsame Punkte: Brennpunkte der Skalen-Ellipse),
           blau: Peillinien (Geraden, -23,5° ≥ δ ≥ +23,5°, annähernd gemeins. Punkte: Seasonal Markers) und
           schwarz: Punkte L, G und K gelten für δ=0° (Durchmesser des Lambert'schen Kreises ist unendlich groß),
           Anmerkung 7, [3]

Roger Bailey bemerkt zu den Lambert'schen Kreisen, nachdem er von Fer de Vries (ein bekannter Sonnenuhren-Theoretiker) auf sie aufmerksam gemacht wurde, dass sie im Unterschied zum Peilen über die Seasonal Markers eine "exakte Lösung" (zutreffend !) und ein "schlüssiges Konzept" (nicht zutreffend !) seien. Seine Kritik geht nicht auf die Selbsverständlichkeit ein, dass eine Peillinie gerade sein muss, nicht kreisförmig sein kann.

Die Lambert'schen Kreise führen exakt durch die Brennpunkte der Ellipse, während sich die Peil-Linien nur mehr oder weniger näherungsweise in je einem ein- für allemal zu bestimmenden Seasonal Marker treffen (Abb.n 2 und 3). Das Peilen ist aber eine einfach durchführbare Arbeit, wohingegen die täglich neue Konstruktion der Skalenpunkte für Sonnenauf- bzw. -untergang durch Zeichnen eines Lambert'schen Kreises auf der Zifferblattebene als deutlich unpraktikabel ausgeschlossen werden muss.

Bailey ging von der Frage aus, ob sich mit Hilfe des Schattenstabs einer analemmatischen Sonnenuhr und einem weiteren Punkt auf ihr in Richtung des Sonnenauf- bzw. -untergangs peilen lasse. Könnte man damit anstatt mit individuellen Markierungen am Horizont oder mit individuellen Megalithen in Steinkreisen (z.B. in Stonehenge) diese Richtungen sogar täglich feststellen? Aus Symmetriegründen (wegen ±-Werten der Sonnendeklination δ sind die Werte der Morgen- bzw. Abendweite symmetrisch zur reinen Ost-West-Richtung) muss ein solcher Punkt auf der großen Ellipsenachse liegen. Da der Ellipsen-Mittelpunkt ausscheidet, wird es sich um zwei Punkte handeln: einer für Sonnenauf- und einer für -untergang.

Baily zog eine Linie vom Fußpunkt des für eine beliebige Sonnendeklination δ (Datum) eingestellten Schattenstabs in die bekannte Richtung des Sonnenaufgangs. Deren rückwärtige Verlängerung (identisch mit der Schattenlinie des Stabes) schneidet die große Hauptachse im von ihm zum Seasonal Marker erklärten Punkt und führt selbstverständlich weiter zum Skalenpunkt der Sonnenaufgangszeit. Nachdem er diesen Vorgang für mehrere Werte aus dem möglichen Bereich ±23,5° der Sonnendeklination δ wiederholt hatte, stellte er fest, dass alle konstruierten Linien sich nahezu im gleichen Seasonal Marker treffen (Abb.3).

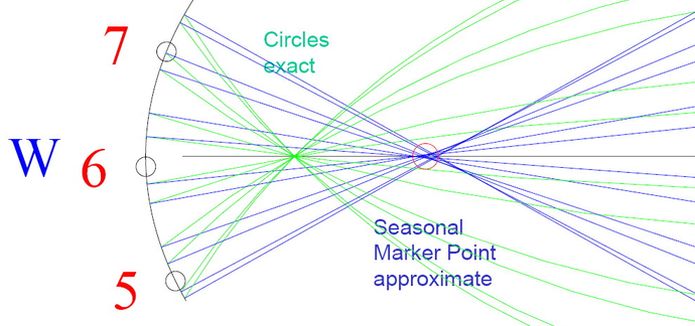Abb.3  Analemmatische Sonnenuhr für geographische Breite φ = 36,9° N, vergrößerter Ausschnitt von Abb.2, links
           grün: Lambert'sche Kreise (-23,5° ≥ δ ≥ +23,5°, gemeinsamer Punkt: ein Brennpunkt der Skalen-Ellipse) und
           blau: Peillinien (Geraden, -23,5° ≥ δ ≥ +23,5°, annähernd gemeinsamer Punkt: Seasonal Marker), [3]

Bailey gab für die Streuung der Schnittpunkte auf einer analermmatischen Sonnenuhr mit 2,5 m großer Halbachse folgende Werte an [3]:

φ = 32° bis 36,9°:   3 bis 4 cm (entspricht 1,2% bis 1,6% der großen Halbachse)
"höhere Breiten" )*: bis 7,5 cm (entspricht bis 3% der großen Halbachse)
)*: gemeint ist vermutlich " bis φ = 51° ", die Breite von Baily's Wohnort (Nähe Calgary)

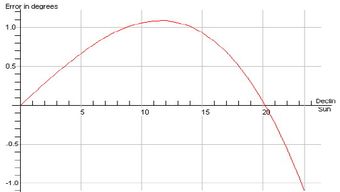<< Abb.4  Peilfehler mit für δ=20,2° ermittelten
                "mittleren" Seasonal Marker (φ=48°), [5]

2.1  zum Näherungs-Charakter des Peilens über die Seasonal Markers    ↑ Anfang

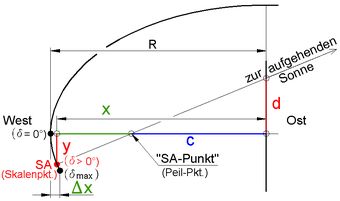<< Abb.5  Teilung der Strecke x im Verhältnis d/y

Dass die Verwendung eines einzigen Seasonal Markers keine exakte Lösung sein kann, sondern eine Näherungslösung ist, wäre auch vor dem Probieren erkennbar gewesen. Mit den allgemein bekannten Formeln für die Datumsweite d (Versatz des Schattenstabes in Nord-Süd-Richtung aus der Ellipsen-Mitte) und für den Wert der y-Koordinate des Skalenpunktes bei Sonnenauf-/-untergang ist schnell erkannt, dass diese beiden Werte zueinander - unabhängig von der Sonnendeklination δ - in einem konstanten Verhältnis stehen:

d = R tanδ cosφ     sinΔτ = tanφ / cotδ     y = R sinΔτ sinφ     (x = - R cosΔτ)
d: Datumsweite ([1 Anhang]     Δτ: Δ der halben Tageslänge (Bezug: 6 Stunden; [6 Gl. in Abb.6])    
d / y  =  1 / tan²φ .

Die Strecke x wird gemäß Strahlensatz im Verhältnis d/y in die Strecken c und (x-c) geteilt (Abb.5). Weil x nicht konstant, sondern wie hier von Interesse von δ ( indirekt über Δτ=f(δ) ) abhängt, ist die Strecke c, die die Lage des Seasonal Markers bestimmt, auch nicht konstant groß.

2.2  Abhängigkeit von der geographischen Breite    ↑ Anfang

Die Genauigkeit des Peilens über einen "mittleren" Seasonal Marker hängt - wie bereits erwähnt - von der geographischen Breite φ ab. Im Folgenden werden die entsprechenden Betrachtungen über "mittlere Breiten" (etwa φ = 40 bis 50°) hinaus auf andere Breiten ausgedehnt (Abb.6).

In niedrigen Breiten ist der Peilfehler wegen Δx << R (Δx: s. Abb.5) sehr klein. Am Äquator (φ=0) ist er Null (Δx=0) und wächst bis zum Polarkreis, wo er mit Δx = R maximal ist, stetig. Höher als am Polarkreis ist er nicht mehr definiert: Die Sonne geht während eines Teils des Jahres nicht unter und während des anderen Teils nicht auf.In diesen Zeiten gibt es keinen täglichen Sonnenauf-/-untergang.

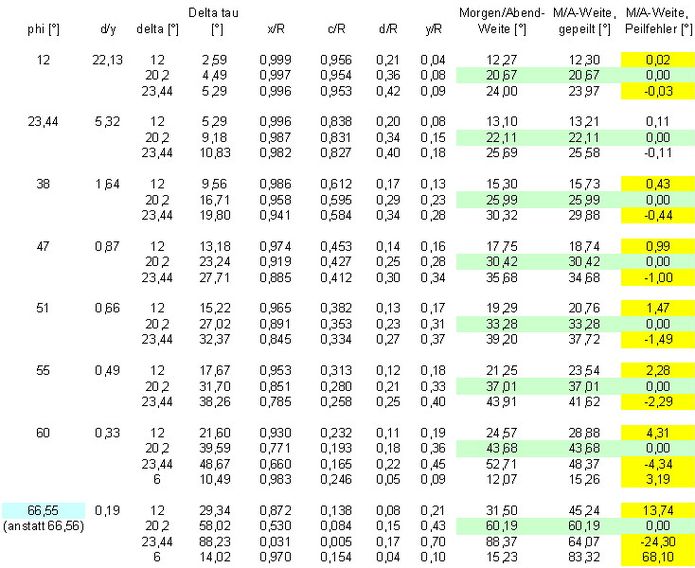Abb.6  Peilfehler für einige georaphische Breiten (φ = 12° bis 66,55° (knapp unter Polarkreis)) bei für die
           Sonnendeklination δ = 20,2° exakt gültigen Seasonal Markers,
           Rechnungen im Wesentlichen mit den unter 2.1 angegebenen Gleichungen
           (Morgen-/Abendweite: [6 Gl. in Abb.6])

Die von Bailey und Sonderegger angegebenen, praktisch erträglichen Peilfehler für "mittlere Breiten" werden bestätigt. Nur wenig nördlich von Deutschland ist der Peilfehler bereits nicht mehr vernachlässigbar (etwa ±2,3° bei φ=55° (Kopenhagen)) und in Nordeuropa nicht mehr akzeptierbar (etwa ±4,3° bei φ=60° (Helsinki)). Weiter nördlich ist die Arbeit mit einem "mittleren" Seasonal Marker sinnlos; die Morgen-/Abendweite variiert am Polarkreis zwischen 0° und ±90°.

Der Vorschlag Sonderegger's, die "mittleren" Sesonal Marker mit δ=20,2° zu ermitteln, wird unterstützt: die Absolutwerte der Peilfehler sind in allen Breiten (mit Ausnahme der Grenzsituation an den Polarkreisen) jeweils für δ=±12° und δ=±23,44° etwa gleich groß (z.B. φ=47°: 0,99 ≈ 1,00)

3. Literatur und Bildnachweise  ↑ Anfang

[0]  J.H.Lambert: "Beyträge zum Gebrauch der Mathematik und deren Anwendung", 2. Teil, 1. Abschnitt,
      "X. Anmerkungen und Zusätze zur Gnomonie, 1. Anmerkungen über die Azimuthaluhren", Berlin, 1770
[1]  S.Wetzel: "Modell für die Ableitung der analemmatischen Sonnenuhr aus einer äquatorialen Ring-Sonnenuhr",
      DGC-Jahresschrift 2004
[2]  S.Wetzel: "Eine mathematische Beschreibung der Analemmatischen Sonnenuhr" ,
      DGC-Mitteilungen Nr.108, 2006
[3]  R.Bailey: "Seasonal Markers for Analemmatic Sundials",
      The Compendium - Volume 10 Number 3, September 2003, Seiten 1 bis 7
      (variierter Reprint als online-.pdf-file, zitierte Bilder von Seiten 14 und 15)
[4]  R.R.J.Rohr: "Der Lambertsche Kreis",
      Schriften der Freunde alter Uhren, 1989, Seiten 129 bis 137
[5]  H.Sonderegger: "Analemmatic Sundials and Mean Time",
      The Compendium - Volume 10 Number 3, September 2003, Seiten 8 bis 13 (zum Thema: Seiten 9 und 10)
      (Reprint als online-.pdf-file, Zitat und Bild von Seite 3 / Page 10)
[6]  S.Wetzel: "Sonnen-Sektor, eine vielseitige Gartenplastik",
      DGC-Jahresschrift 2006

4. Anmerkungen/Anhänge  ↑ Anfang

Anmerkung 1:  ↑ zurück

Johann Heinrich Lambert ist auch der Zweit-Erfinder der sogenannten analemmatischen Foster-Lambert-Sonnenuhr.

Anmerkung 2:  ↑ zurück

Exzentrizität e = (a²-b²) ^½ ;  a = R ;  b = a sinφ ;  >>  e = - R cosφ .

Anmerkung 3:  ↑ zurück

Rohr gibt das gleiche Ergebnis an, das er vermutlich mit Hilfe der xy-Koordinaten des Brennpunktes F erhält. Da ich seinem Rechenweg (mir unverständliche Gleichung (III) auf S.133, die wegen eines zusätzlichen, linear von y abhängigen Terms keine Mittelpunktgleichung ist) nicht folgen kann, hänge ich meine eigene Rechnung an. In die Mittelpunktgleichung des Kreises setze ich die Brennpunkt-Koordinaten ein. Dabei ist zu beachten, dass das Koordinatensystem des Kreises gegenüber dem der Ellipse nach unten verschoben und die die y-Koordinate von F nicht Null ist. Die positive x-Achse zeigt nach rechts, die positive y-Achse nach oben (Abb.1)

x,y                    Koordinaten des Brennpunktes F,
x² + y² = r²         Mittelpunktgleichung des Kreises,
x = e = - R cosφ       >>    x² = R² cos²φ,
y = r - d             (wertgleich mit Koordinatenverschiebung Δy),
d = R tanδ cosφ,
y = r - R tanδ cosφ    >>    y² = r² - 2 r R tanδ cosφ + R² tan²δ cos²φ,
x² + y² = r²                >>    R² cos²φ + r² - 2 r R tanδ cosφ + R² tan²δ cos²φ = r²,
R cos²φ - 2 r tanδ cosφ + R tan²δ cos²φ = 0,
r = R cosφ (1 + tan²δ) / 2 tanδ,     mit Hilfe des Additionstheorem   (1 + tan²δ) / 2 tanδ = 1 / sin2δ   wird daraus:
r = R cosφ / sin2δ , qed.

Anmerkung 4:  ↑ zurück
Schlägt man mit der Länge GL als Radius einen masstäblichen Kreisbogen über die Ellipse, so wird diese im Punkt L tangiert. Das ist eine anschauliche Bestätigung für Lambert's Normalen/Tangenten-Aussage.

Anmerkung 5:  ↑ zurück

Rohr erkennt offensichtlich nicht, dass er den Satz des Thales anwendet. Dass am Punkt L ein rechter Winkel über dem Durchmesser des Lambert'schen Kreises vorliegt, schlussfolgert er mit dem Hinweis (s. S.133): Der Streifschatten bei Sonnenaufgang "stößt als Normale auf den Ellipsenbogen und seine Tangente." Damit wiederholt er merkwürdigerweise die von ihm als "etwas unklar" beurteilte Lambert'sche , die für die vorliegende Berechnung weder erforderlich ist, noch durch sie überprüft wird.

Rohr erkennt auch die Unabhängigkeit der Länge GL von φ offensichtlich nicht. Er schleppt einen entsprechenden, φ enthaltenden Ausdruck (s. S.134/135, Abb.4) weiter und erhält ein aufgeblasenes Zwischenergebnis, bei dessem Vereinfachung diese Schein-Abhängigkeit dann selbstverständlich entfällt.

Anmerkung 6:  ↑ zurück

Die folgende Kontrollrechnung zeigt, dass die Punkte auf der großen Ellipsenachse, in denen sich alle Lambert'schen Kreise (δ variabel, φ konstant) schneiden, die Brennpunkte sind:
Der Abstand der Brennpunkte F u. F' von der Ellipsenmitte ist die Exzentrizität e und ist gleich der x-Koordinate für ihre Eigenschaft als auf den Lambert'schen Kreisen liegende Punkte:
e = x = ± R cosφ.
Die mit d und r bekannte
y-Koordinate dieser Punkte ist
y = r - d = R (cosφ/sin2δ - cosφ tanδ).
In die Mittelpunktgleichung des Kreises
x² + y² = r²
eingesetzte Ausdrücke der bekannten Größen y und r ergeben:
x² = R² ((cosφ/sin2δ)² - (cosφ/sin2δ - cosφ tanδ)² ,
x² = R² cos²φ ((1 sin2δ)² - ( sin2δ)² + 2 tanδ/sin 2δ - tan²δ) .
Die ersten beiden Summanden ergeben Null, die beiden folgenden Eins, was mit Hilfe des Additionstheorems
1/sin2δ = (1 + tan²δ) / 2 tanδ
erkennbar ist:
(2 tanδ / sin 2δ) - tan²δ = 2 tanδ (1 + tan²δ) / 2 tanδ - tan²δ = 1 + tan²δ - tan²δ = 1 .
Somit ist
x = ± R cosφ,  qed.

Anmerkung 7:  ↑ zurück

Die Skalierung ist für wahre Zonenzeit (wahre Sonnenzeit auf dem Bezugslängengrad) vorgenommen, wobei sich der Aufstellungsort der Uhr etwas westlicher als der Bezugslängengrad befindet.

Anmerkung 8:  ↑ zurück

Der Wert δ = ±20,2° wird als ausreichende Näherung auch für andere Werte von φ empfohlen.

5.  Nachtrag:
     eine Veröffentlichung vom Dez. 2014 zum gleichen Thema  ↑ Anfang

di Giovanni Ferrari: "I cerchi di Lambert e i Seasonal Markers nelle meridiane analemmatiche",
                                 Orologi Solari - n. 6 - dicembre 2014.

Seiten 41 bis 47: L'articolo di Lambert
Der Artikel von Lambert

Der Autor bezieht sich auf die originale Arbeit von Lambert [0]. Die Arbeit von Rohr [4] bleibt unerwähnt. Die bereits von Rohr zitierte und als "etwas unklar formuliert" beurteilte Aussage Lambert's ist als Faksimile beigefügt und auch für diesen Autor Anlass, selbst nach Klarheit zu suchen.

Sein Ansatz, die bekannte Normalengleichung der Ellipse im Skalenpunkt z.B. des Sonnenuntergangs anzuwenden und zu zeigen, dass die gefundene Normale durch den Fußpunkt G des Schattenstabs verläuft, ist erkennbar. Die Durchführung dieses Vorhabens in klaren Schritten zwischen Ausgangslage und Ergebnis ist aber nicht vorgenommen.

Dem Ansatz, mit der Normalengleichung zu arbeiten, bin ich selbst wie folgt nachgegangen.

Gleichung für Normale auf Punkt U (SonnenUntergang) der Ellipse:   a² ( (x/x_U) -1 ) = b² ( (y/y_U) -1 ).
Die x-Koordinate des Punktes G ist x = x_G = 0. Zu finden ist die zugehörende y-Koordinate y = y_G. Deshalb:
Umstellung der Normalengleichung und x=0 einsetzen:   y = y_G = y_U ( 1 - a²/b² ).
Für den Stundenwinkel Τ bei Sonnenuntergang gilt:   cos Τ = - tan φ · tan δ.   (siehe Anmerkung A)
(φ = geographische Breite, δ = Deklinationswinkel der Sonne)
Die y-Koordinate des elliptischen Skalenpunktes für den Sonnenuntergang ist:   y_U = a · cos Τ_U · sin φ.
Mit dem Stundenwinkel ist:   y_U = - a · tan φ · tan δ · sin φ.
Das quadratische Verhältnis der Halbmesser der Skalenellipsen ist:   a²/b² = 1 / (sin² φ).  
Und mit dieser y-Koordinate und diesem Halmesserverhältnis ist:

y_G = a · tan δ · cos φ .

Die Vorschrift für das täglich veränderte Aufstellen des Schattenstabs lautet bekanntlich gleich:

y_G = a · tan δ · cos φ . (siehe Anmerkung B)

Ergebnis:
Der mittels Normalengleichung gefundene Abstand des Stabfußpunktes von der großen Ellipsenachse stimmt überein mit dem mittels Vorschrift für das Aufstellen des Stabs gefundenen Wert.

Seiten 48 bis 51: Punti indicatori dell'alba e del tramonto - Seasonal Markers.
Die Peilpunkte für Sonnenauf- und -untergang - Seasonal Markers

Der Autor bespricht den einschlägigen Anteil in der Arbeit von Bailey [3] und stellt wie bereits Sonderegger [5] vor ihm Berechnungen darüber an, wie groß der Fehler des Peilens über einen gemittelten Seasonal Marker zum Sonnenauf-/-untergangspunkt am Horizont bzw. zu den entprechenden Skalenpunkten ist. Er empfiehlt, als diesen Punkt den für δ= 20,3° berechneten zu verwenden (Sonderegger: 20,2°).

Das folgende Foto befindet sich auf der letzten Seite der besprochenen Arbeit. 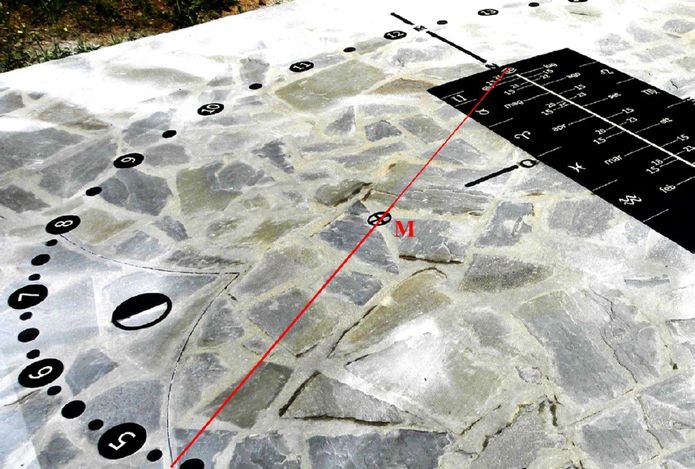Abb.7  Analemmatische Boden-Sonnenuhr für geographische Breite φ = 44,1° N: Peilung über Seasonal Marker M
           vom Fußpunkt des (verschieblichen, nicht abgebildeten) Gnomons zum Stundenpunkt des Sonnenaufgangs
           (Datum: Sommersomnnenwende; Gegenrichtung: zum Horizontpunkt des Sonnenaufgangs)
           Teile der Lambert'schen Kreise für Sommer- (links unten) und Wintersonnenwende (links oben ) auf dem
           Boden markiert
           Stundenskala: wahre Ortszeit für geographische Länge 15° Ost (Uhrenstandort: 11° Ost)

Anmerkung A:   sin ΔΤ = tanφ / cotδ  [6 Abb.6]     >>   = sin (Τ-90°)     >>>     cos Τ = - tan φ · tan δ.
Anmerkung B:   d = R·tanδ·cos φ  [1 Anhang/Schattenstab-Skala]   >>>   y_G = a·tanδ·cos φ  (mit d=y_G und R=a).

Siegfried Wetzel, CH 3400 Burgdorf, September 2014 (Dez.14 / Juni 17)

 ↑↑ Anfang
<< andere Sonnenuhren-Beiträge
<< Home