<< Home
<< andere Sonnenuhren-Beiträge
↓↓ Ende
Eine mathematische Beschreibung der Analemmatischen Sonnenuhr
(DGC-Mitteilungen Nr.108, 2006)
Inhalt
1. Einleitung
2. Die Parameter-Form der Ellipse
3. Koordinaten-Transformation
4. Das Azimut der Sonne
5. Der Höhenwinkel der Sonne
6. Literatur
7. Anmerkungen
1. Einleitung ↑ Anfang
Die Analemmatische Sonnenuhr wird auch Elliptische Sonnenuhr genannt. Somit ist naheliegend, sie einmal mit einer Ellipsen-Gleichung zu beschreiben. Ihr Dritt-Name in der hier behandelten Standard-Version (horizontale Ellipse, vertikaler Schattenstab) lautet Azimutale Sonnenuhr. Man kann sie leicht mit einer Azimut-Skala ergänzen. Der verwendete Schattenstab täuscht darüber hinweg, dass für die Anzeige des Stundenwinkels nur ein die Sonne abbildender Punkt verantwortlich ist. Wenn man diesen momentan wirksamen Punkt auf dem Stab bestimmt, findet man gleichzeitig auch den momentanen Höhenwinkel der Sonne.
Der üblichen Herleitung der Analemmatischen Sonnenuhr aus einer Äquatorialen Ring-Sonnenuhr durch Parallel-Projektion [1] habe ich die Herleitung durch Parallel-Verschiebung aus einer solchen in Teile zerlegten Sonnenuhr gegenüber gestellt [2], [3]. Das hat den Vorteil, dass der Ortswechsel des abbildenden Punktes in der Erklärung eingeschlossen ist. In der vorliegenden Arbeit benutze ich für den Übergang von der einen zur anderen Sonnenuhr die Koordinatensysteme des Ortsäquators und des Horizonts. Der Begriff Verschiebung (oder nur Schiebung) taucht allgemein wieder auf, weil sich mit dem abbildenden Punkt der in ihm befindliche Koordinaten-Ursprung dauernd verschiebt. Die vorgenommene Transformation zwischen den beiden Koordinaten-Systemen ist ausserdem als Parallel-Betrachtung zur Ellipsen-Gleichung gedacht.
2. Die Parameter-Form der Ellipse ↑ Anfang
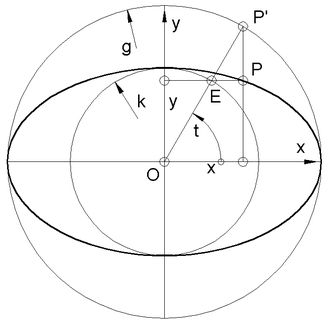
<< Abb.1 Ellipse, Parameterdarstellung und Konstruktionsmethode
Aus dem Skalenkreis der Äquatorialen Ring-Sonnenuhr wird die Ellipse der Analemmatischen Sonnenuhr. Deren Parameter-Darstellung der Normalform (d.h., wenn die Koordinatenachsen mit den Ellipsenachsen zusammenfallen) lautet allgemein [4, Seite176] (Abb.1):
(1) x = g cos t y = k sin t .
In dieser Darstellung ist eine bekannte Konstruktionsmethode für die Ellipse, die sich auch hier zum Zeichnen der elliptischen Skala eignet, enthalten:
Man zeichne die beiden Kreise mit Radius g und k und einen Strahl OP', projiziere den Schnittpunkt E auf die Senkrechte durch P', dann ist P ein Punkt der Ellipse.
Die Ellipse in Abb.2 ist die Skala der Analemmatischen Sonnenuhr. Für sie ist das in der Astronomie übliche Koordinatensystem des Horizonts verwendet. x- und y-Achse sind gegenüber Abb.1 vertauscht. Die positiven Achsen zeigen im Gegensatz zum Astronomischen System nach Nord (x) bzw. Ost (y), weil nicht der Ort der Sonne sondern der ihres (Schatten-) Bildes gekennzeichnet wird (Anmerkung 1). Die beiden Parameter-Ausdrücke lauten hier:
(2) y = g cos(90°-τ) x = k sin(90°-τ) .
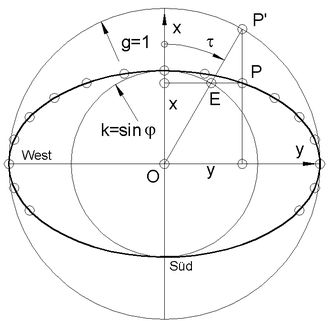
<< Abb.2 Analemmatische Sonnenuhr, elliptische Skala
Zwischen Äquatorialer Kreisskala und Analemmatischer Ellipse besteht die bekannte Beziehung:
kleine Ellipsen-Achse k = g sinφ (g = Radius des Kreises,
φ = geographische Breite). Wir wählen den Einheits-Radius
(g = 1), dann ist k = sinφ . Anstatt t ist in Abb.2 der Stundenwinkel τ der Parameter (Anmerkung 2). Die beiden Parameter-Ausdrücke für die Analemmatische Ellipsen-Skala lauten schliesslich so:
(3) y = sinτ x = sinφ cosτ .
Die grosse Halbachse ist 1, die kleine ist sinφ .
3. Koordinaten-Transformation ↑ Anfang
Der Übergang vom Äquatorialen Ring zur Analemmatischen Ellipse ist auch an Hand der Koordinaten-Transformation des Bildpunktes der Sonne vom Ortsäquatorsystem ins System des Horizonts zu verfolgen. Die Transformationsformeln lauten
[5, Seite 20]:
(4) y = cosδ sinτ x = sinφ cosδ cosτ - cosφ sinδ
(4a) z = cosφ cosδ cosτ + sinφ sinδ
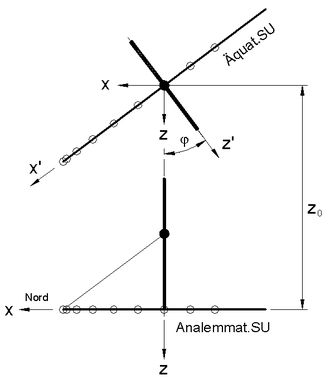
<< Abb.3 Koordinatentransformation und Verschiebung z0 bei δ=0
Bei üblicherweise gleichem abbildenden Punkt geht das Horizont-System lediglich durch die Drehung (90°-φ) um die y- (Ost/West-) Achse aus ersterem hervor. Aber:
Das Analemmatische Zifferblatt ist eine horizontale Ebene, in die alle Bildpunkte aus der zu ihr geneigten Äquatorebene vertikal (vorwiegend gegen Zenit) verschoben gedacht sind. Die Verschiebung ist der Wert der z-Koordinate (Horizont-System), die für jeden Bildpunkt anders ist. Die abbildenden Punkte machen die Verschiebung mit. Sie sind über den Tag (δ=const, nur τ=variabel) auf einer vertikalen Geraden verteilt, in die der Schattenstab zu setzen ist. Dieser Punkt-Vielfalt entspricht eine Vielzahl von Koordinaten-Systemen (Horizont-), weil deren Ursprung ja der jeweilige abbildende Punkt ist.
Im Folgenden wird deshalb die vertikale Dimension z nicht weiter beachtet (ausser der Verschiebung z0 des Analemmatischen Zifferblattes gegen Nadir, damit die beiden Sonnenuhren nicht ineinander liegen). Das bezüglich der z-Koordinate Gesagte lautet kurz mit anderen Worten:
Alle individuellen schattenwerfenden Punkte befinden sich auf einer Geraden. Die Materialisierung dieser Geraden ist der senkrechte Schattenstab [2, Seite 195].
Abb.3 beinhaltet den Sonderfall δ = 0, wobei die Koordinatenachsen des Horizont-Systems mit denen in Abb.2 identisch sind. Mit δ = 0 vereinfachen sich die Formeln (4) und werden mit den Ausdrücken (3) identisch, qed.
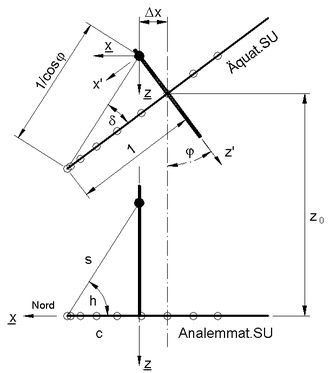
<< Abb.4 Koordinatentransformation und Verschiebung z0 bei δ≠0
Den allgemeinen Fall δ≠0 zeigt Abb.4. Die Koordinaten-Ursprünge folgen der Wanderung des abbildenden Punktes auf dem Polstab (Äquatoriale Ring-Sonnenuhr) bzw. der Verschiebung des Schattenstabes (Analemmatische Sonnenuhr). Die horizontale Veränderung hat den Wert Δx = cosφ tanδ , um den wir das ursprüngliche Koordinaten-System der Ellipse (zusammen mit dem Schattenstab) verschieben (Abb.2 →Abb.5).
Die Ausdrücke (3) ändern mit x = x -Δx vorerst zu:
(5) y = sint x = sinφ cosτ - cosφ tanδ .
Sie sind mit dem Faktor cosδ zu verkleinern, um sie mit den allgemeinen Transformationsformeln (4) vergleichen zu können, denn in diesen befindet sich die Sonne bzw. ihr Bild auf einem Kleinkreis, wenn δ ≠ 0. In unserem Modell behalten wir aber den Grosskreis Äquator-Ring bzw. seine entsprechende Ellipse bei jedem Wert von δ bei. Der Schattenstrahl hat die Länge 1/cosδ (ist also variabel und länger als der Einheits-Radius, s.Abb.4 oben).
Die verkleinerten Ausdrücke lauten:
(6) y cosδ = y = cosδ sinτ
x cosδ = x = sinφ cosτ cosδ - cosφ sinδ ,
sind somit mit den Transformationsformeln (4) identisch, qed.
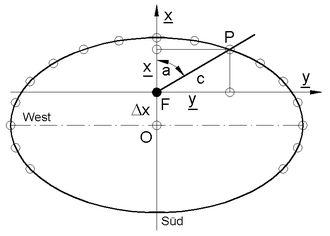
<< Abb.5 Analemmatische Sonnenuhr, Schattenstabverschiebung Δx bei δ≠0
4. Das Azimut der Sonne ↑ Anfang
Das Azimut ist eines der beiden im Horizontsystem gebrauchten Bestimmungsstücke für den Ort der Sonne. Der senkrechte Stab repräsentiert einerseits die z-Achse dieses Systems, und andererseits kennen wir die Richtung des Schattens eines solchen Stabes als die anschaulichste Erklärung für das Azimut (genauer: die Richtung, aus der der Schatten kommt). Also bedarf es zur Anzeige desselben auf einer Analemmatischen Sonnenuhr nur einer zusätzlichen Skala (Windrose), wodurch schliesslich der Grund für den Drittnamen dieser Uhr sichtbar wird (Abb.6).
Der Quotient der beiden Ausdrücke der Parameterform der Ellipsengleichung führt zum Azimut a der Sonne (selbstverständlich ebenso der Quotient der beiden Transformationsformeln (4)):
(7) tan a = y/x = sinτ / (sinφ cosτ - cosφ tanδ ) .

<< Abb.6 Analemmatische Sonnenuhr mit zusätzlicher Windrose zur Azimut-Anzeige,
5. Der Höhenwinkel der Sonne ↑ Anfang
Es bleibt noch zu fragen, wo der Höhenwinkel h, das zweite Bestimmungsstück im Horizont-System, in der Analemmatischen Sonnenuhr versteckt ist. In den Transformationsgleichungen ist er als z-Koordinate angegeben:
(4a) z = sin h = cosφ cosδ cosτ + sinφ sinδ .
In der z-Achse befindet sich der Schattenstab. Also ist auf diesem nur der entsprechende Koordinatenpunkt zu finden. Das ist durch eine Peilung (Abb.7) möglich. Auf dem Schattenstab wird ein horizontaler Stift derart in der Höhe verschoben, dass sein Schatten auf die Ellipse fällt. Auf einer mit diesem Stift verbundenen kleinen Zusatzskala entsteht auch ein (streifender) Schatten, der den Höhenwinkel direkt angibt (Anmerkung 3).

<< Abb.7 Analemmatische Sonnenuhr mit zusätzlichem Schieber auf Schattenstab zur Höhen-Messung
(für besser erkennbaren Schatten des Querstabes auf Ellipse s.Abb.6)
Abschliessend lässt sich in einer Rechnung zeigen, dass die Länge des Stabschattens c (s.Abb.5) zwischen Fusspunkt F und Kreuzungspunkt P mit der Ellipse ebenfalls ein Mass für die Sonnen-Höhe ist. Er ist Hypotenuse des rechtwinkligen Dreiecks mit den Katheten y und x (c2 = y2+ x2). Im Höhen-Dreieck über dem Stabschatten (Abb.4, der Einfachheit halber ist hier der Fall τ=0 gezeichnet) gilt;
(8) cos h = c/s .
Zur Wiederholung: Der Schattenstrahl s hat die Länge
s = 1/cosd.
Auf die Darstellung der etliche Zwischenschritte benötigenden Umwandlung von (8) in der Form sin2h = f(φ,δ,τ) zum Vergleich mit der ebenfalls quadrierten z-Koordinate (4a) der Transformationsgleichungen wird hier verzichtet.
Da die Umwandlung nicht ganz einfach ist, sei verraten, dass ich weiter kam, als ich die bei der Umwandlung der linken Seite von (8) mit cos2 h = 1 - sin2 h hinzukommende 1 zu sin2δ + cos2δ umformte. Die erwartete Identität stellte sich ein, qed.
6.Literatur ↑ Anfang
[1] P.Terpstra: "Zonnewijzers", Groningen und Djakarta 1953
[2] S.Wetzel: "Sonnenuhren mit zusätzlicher Weltkarte auf dem Zifferblatt",
Schriften der Freunde alter Uhren, 1998
[3] S.Wetzel: "Ein Modell für die Ableitung der Analemmatischen Sonnenuhr aus einer Äquatorialen Ring-Sonnenuhr",
DGC-Jahresschrift 2004
[4] Bronstein-Semendjanew: "Taschenbuch der Mathematik", Leipzig 1960
[5] H.Schilt: "Koordinatensysteme der Astronomie" und "Koordinaten-Transformationen",
ORION-Sondernummer 1980
7. Anmerkungen ↑ Anfang
Anmerkung 1: Das Koordinatensystem der Astronomie ist 180° um die z-Achse gedreht und zur x-y-Ebene gespiegelt: die positive z-Achse zeigt zum Nadir, aus dem Links- ist ein Rechts-System geworden. ↑ zurück
Anmerkung 2: In der Ellipsen-Gleichung ist der Kreis als Sonderfall enthalten (g = k). In unserem Fall ist es der Äquatorkreis, in dem wir ohne Mühe den Stunden- als Kreiswinkel bzw. Parameter erkennen. ↑ zurück
Anmerkung 3: Der gefundene Punkt repräsentiert den grösseren Wert z ( = z /cosδ, s. Abschnitt 3.), von ihm geht aber auch der längere Schattenstrahl 1/cosδ aus, so dass im proportional grösseren Höhen-Dreieck auch
sin h = z / (1/cosδ) = z / 1 = z ist. ↑ zurück
![]() Siegfried Wetzel, CH 3400 Burgdorf, Januar 2008
Siegfried Wetzel, CH 3400 Burgdorf, Januar 2008
↑↑ Anfang
<< andere Sonnenuhren-Beiträge
Druck-Version (2-spaltig, 4 Seiten, *.pdf, 320 kB) >>
<< Home