<< Home
<< andere Mechanik-Beiträge
↓↓ Ende
Elastische Balken als Bestandteile von Feder-Gelenken
Beziehungen zwischen den Biegelinien von drei verschieden gelagerten und belasteten Balken konstanten Querschnitts
siehe auch Elbe-Brücke "Blaues Wunder" −
Mutmaßungen über die in ihr enthaltenen Feder-Gelenke
Inhalt
1. Einleitung2. Zwei- und Dreiblatt-Federgelenke von Claus Köpcke
3. Beziehungen zwischen den Biegelinien von drei verschieden gelagerten und belasteten Balken
konstanten Querschnitts
4. Einblatt-Federgelenk und Kreuz-Federgelenk
5. Untersuchung eines Zweiblatt-Federgelenks von Claus Köpcke
5.1 vertikale Feder
5.2 horizontale Feder
5.3 Versuche an einem Modell des Zweiblatt-Federgelenks
6. Ausklang
7. Anmerkungen
8. Literatur
1. Einleitung ↑ Anfang
Im Artikel über die Elbe-Brücke "Blaues Wunder" von Claus Köpcke [1] in Dresden befasste ich mich mit den darin zwischen den vier großen massiven Brückenteilen und den Verankerungen an den Ufern eingebauten "Feder-Gelenken". Die als Blattfedern dienenden relativ dünnen Elemente verhalten sich wie schlanke, lediglich breite Balken. Die hier für Gelenkigkeit ausgenutzte elastische Biegung eines einzelnen solcher Balken in jeweiliger Einspannung an seinen Enden ist in technischen Nachschlagewerken "katalogisiert" beschrieben. In der vorliegenden Brücke werden an den Gelenk-Stellen aber zwei bis drei Federblätter verwendet (Abb.1), die sich nicht wie z.B. beim bekannten Kreuzfeder-Gelenk kreuzen, sondern in einer Ebene nebeneinander angeordnet sind. Die relativ einfache Behandlung durch Überlagern (Superposition) zweier sich gegenseitig praktisch nicht beeinflussender Federblätter wie beim Kreuzfeder-Gelenk ist somit nicht möglich. Aus nur zwei Federblättern besteht am "Blauen Wunder" offensichtlich ohnehin nur das Pylon-Gelenk (Typ A). Dafür leite ich eine näherungsweise Beschreibung her. Die aus drei Federn bestehenden Gelenke lasse ich wegen zu hohem Schwierigkeitsgrad ihrer technischen Beschreibung außer Acht.
Abschnitt 2: Nach Angabe einiger Details zu den Köpcke-Gelenken weiche ich aber vorerst etwas vom direkten Pfad ab,
indem ich mich im ...
Abschnitt 3: ... grundlegend mit drei solchen katalogisierten Standard-Fällen einzelner Federblätter (bzw. Balken mit bestimmter Einspannung und Belastung, [2] und [3]) befasse. Ich gehe der Frage nach, ob der eine dieser Fälle, der eine Annäherung an die vertikale Feder im Pylon-Gelenk ist, als Kombination der beiden anderen und einfacheren Fälle zu verstehen ist. Dass ich anderenseits auch eine Kombination zwischen diesen einfacheren Fällen suche, ist eher einer noch grundlegenderen Neugier geschuldet.
Danach gehe ich im ...
Abschnitt 4: ... kurz auf den aktuellen Stand der Technik von Federgelenken ein.
Erst im letzten ...
Abschnitt 5: ... erfolgt die von einem Modell-Versuch unterstützte Herleitung von Formeln zur o.g. näherungsweisen Berechnung von Köpckes Gelenktyp A.
2. Zwei- und Dreiblatt-Federgelenke von Claus Köpcke ↑ Anfang
Die einander ähnlichen Gelenke F und C von Köpcke (Abb.1) können aus je zwei federnden Stahl-Platten hergestellt werden. Durch die mittige Befestigung wird ihre jeweilige vertikale Platte in zwei Feder-Blätter unterteilt. Ob diese beiden im Vergleich zum Typ A um einen zusätzlichen Grad komplizierten Konstruktionen (3 anstatt 2 voneinander separierte Federblätter) im "Blauen Wunder" angewendet sind, ist mir nicht bekannt. Wenn, dann wäre nur das Anker-Gelenk betroffen, denn die Konstruktion des Scheitel-Gelenks in Brückenmitte ist anders, und sie ist mir relativ gut bekannt (Abbildungen 10 und 12 in [1]).
Ich werde mich deshalb und auch wegen des geringeren Aufwands im Folgenden nur mit dem weniger komplizierten
Typ A befassen
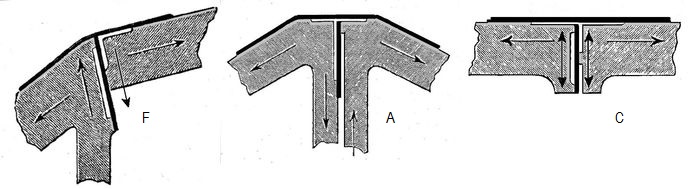 Anker-Gelenk F Pylon-Gelenk A Scheitel-Gelenk C
Anker-Gelenk F Pylon-Gelenk A Scheitel-Gelenk C
Abb.1 Blattfeder-Gelenke nach Köpcke für "versteifte 3-gelenkige Hängebrücke", dessen Prototyp das von ihm
errichtete "Blaue Wunder" ist (Abb.7 in
[1])
3. Beziehungen zwischen den Biegelinien von drei verschieden gelagerten und
belasteten Balken ↑ Anfang
Dieser Abschnitt bezieht sich auf den Untertitel: Beziehungen zwischen den Biegelinien von drei verschieden gelagerten und belasteten Balken konstanten Querschnitts. Die drei Balken (ihre Lagerung und Belastung) sind in technischen Nachschlagewerken "katalogisiert" beschrieben (s. Abb.2).
 Abb.2 "Balken mit verschiedener Lagerung und Belastung" Auszug aus einer Tafel in [2]
Abb.2 "Balken mit verschiedener Lagerung und Belastung" Auszug aus einer Tafel in [2]
Der in der Abb.2 gezeigte Fall 26 erfasst noch nicht genau die Verhältnisse (Einspannung und Belastung) an der vertikalen Feder im Gelenk-Typ A, kommt ihnen aber am nächsten. Ich werde zunächst versuchen, ihn besser zu verstehen, bevor ich mich den ähnlichen, aber doch nicht genau gleichen Verhältnissen im Gelenk-Typ A zuwende. Zum Besser-Verstehen-Wollen gehören Versuche, den Fall 26 als diverse Kombinationen aus den beiden anderen Fällen darzustellen.
Fall 1 + Fall 1 = Fall 2
Eine Kombinations-Übung vorab ist die Darstellung des Falles 2 als "Verdopplung" des Falles 1, siehe Abb.3a.
Der mit dem Biegemoment M = P (l-x) gebogene Balken wird mit dem gleichen, nur in umgekehrter Richtung ansteigenden Biegemoment M = P x belastet und weiter gebogen. Somit werden zwei gleiche, nur um die Vertikale spiegelbildlich verlaufende Biegelinien überlagert mit dem Resultat konstanter Biegung (Krümmung) über die ganze Balkenlänge. Dieser kreisförmigen Biegelinie liegt ein bei der Addition der Biegemomentverläufe entstehendes, über die Balkenlänge konstantes Biegemoment zugrunde (in Abb.2 als M0 bezeichnet; sein Wert in Abb.3a gleich P·l; Anmerkung 1 ).
In Abb.3b ist die Verdopplung etwas anschaulicher dargestellt. Im 1. Schritt wird der Balken links eingespannt und rechts mit P belastet. Im 2. Schritt wird er im gebogenen Zustand rechts eingespannt und mit der Last P am linken Ende nochmals gebogen (Abb.3b, links). Dass der links eingespannte Balken vor dem Biegen nach rechts oben zeigt, ist ein formaler Trick ohne praktische Auswirkung. Die linke Einspannung ist um soviel im Gegenuhrzeigersinn verdreht, dass die Tangente an den gebogenen Balken im rechten Endpunkt horizontal ist. Auf diese Weise hat die Biegelinie nach dem 2. Schritt die gleiche Lage wie in Abb.2, mittig links. Zudem sind die Verformungen f1 und f2 leicht vergleichbar dargestellt, was bei Verzicht auf diesen Trick (Abb.3b, rechts) nicht der Fall ist.
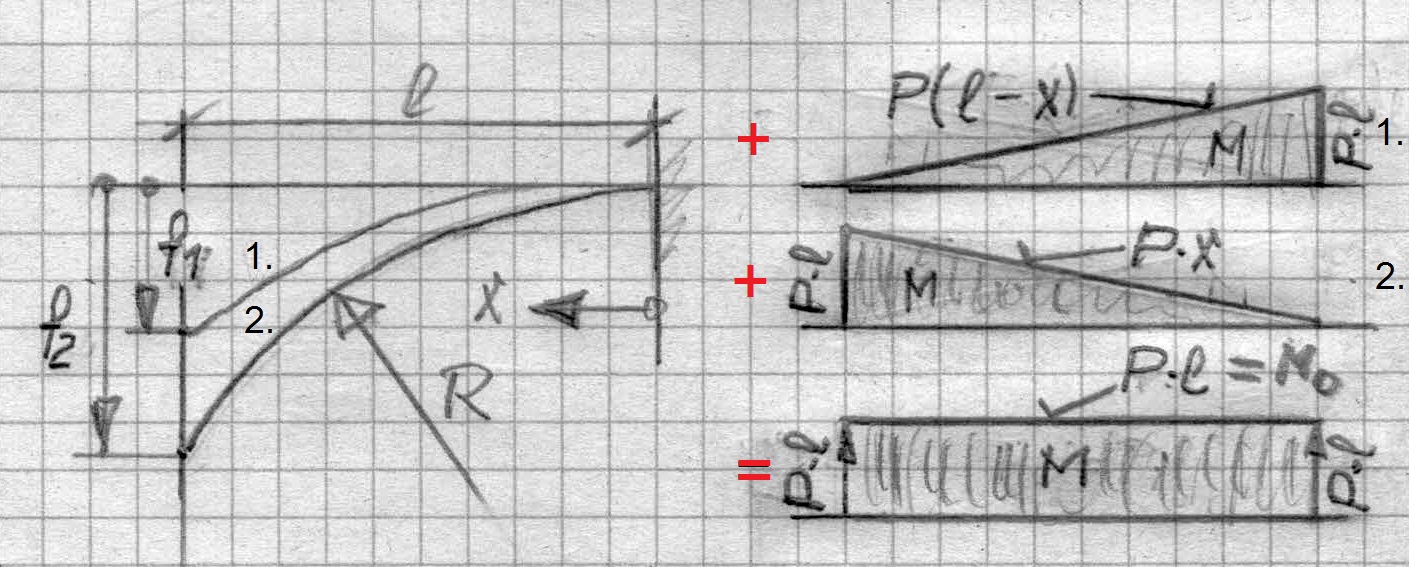 Abb.3a Fall 1 + Fall 1 = Fall 2 (Version 1)
Abb.3a Fall 1 + Fall 1 = Fall 2 (Version 1)
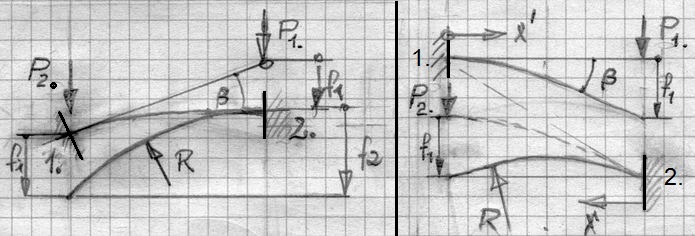 Abb.3b Fall 1 + Fall 1 = Fall 2 (Version 2)
Abb.3b Fall 1 + Fall 1 = Fall 2 (Version 2)
Fall 1 + Fall 1 = Fall 26
Man kann durch "Verdopplung" des Falles 1 auch zum eigentlich interessierenden Fall 26 kommen.
Der Mittelpunkt W der Biegelinie im Fall 26 kann als gemeinsamer Punkt der freien Enden zweier Kragträger (Fall 1) angesehen werden. Beide Kragträger befinden sich an dieser Stelle punktsymmetrisch zueinander: gegeneinander gerichtet, aber auch in Gegenrichtung gebogen (Abb.4). Das Biegemoment hat an den Enden des zusammengesetzten Balkens den absolut gleichen Wert M = P l26/2.
Weil l26 doppelt so groß wie l1 ist ( l26 = 2 l1 ), sind die beiden Momentangaben wie erwartet faktisch gleich:
P l26/2 = P l1 (Abb.2, links unten bzw. oben).
Auch die Angaben für f26 und f1 entsprechen sich wie erwartet : f26 = 2 f1 (Abb.2, rechts unten bzw. oben).
Man muss auch hier l1 durch l26/2 ersetzen: 2 f1 = 2 (P / EI) (l13/3) = (P / EI) (l263/12) = f26 (Anmerkung 2).
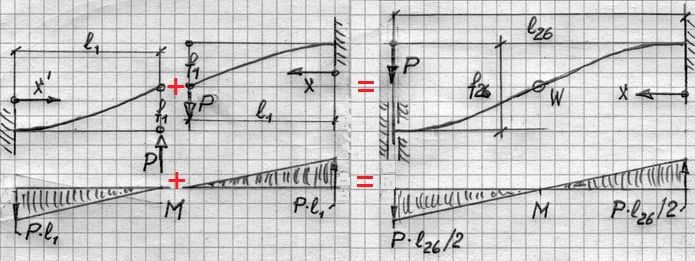 Abb.4 Fall 1 + Fall 1 = Fall 26
Abb.4 Fall 1 + Fall 1 = Fall 26
Schließlich führt auch die Kombination der Fälle 1 und 2 zum Fall 26. Ich habe die Betrachtung dazu meiner detaillierteren Arbeit im Abschnitt 5.1 (Abb.7) vorangestellt.
4. Einblatt-Federgelenk und Kreuz-Federgelenk ↑ Anfang
Bevor ich näher auf Köpckes Federgelenke (insbesondere auf Typ A) eingehen werde, erwähne ich den aktuellen Stand der Technik von Federgelenken.
Das einfache Federgelenk mit einem Federblatt und das Kreuz-Federgelenk mit zwei sich kreuzenden Federblättern werden in der Gerätetechnik häufig angewendet und sind in der Fachliteratur gut beschrieben [4] bis [7]).
Bei diesen Anwendungen sind die zu übertragenden Kräfte klein, die Schwenkwinkel hingegen groß (bis 30° und mehr). Bei Brückengelenken ist das umgekehrt (Schwenkung <1°). Selbst bei 10° Schwenkwinkel, der den bei Brücken und anderen Bauwerken realen Wert um eine Größenordnung übersteigt, verlagert sich der momentane Drehpunkt (Momentanpol) unerheblich, wie die folgende, aus [4] ermittelte Aufstellung zeigt:
Einblatt- Kreuz- Federgelenk
längs quer längs quer y bzw.x (Abb.5)
0,1 2,5 0,05 0,007 Verlagerung in % von l
Mit Hilfe von z.B. eingefügter Drehgelenke werden Brücken u.a. gegen Längenänderungen der Brückenteile durch Temperaturänderungen unempfindlich gemacht. An der Änderung der Gesamt-Geometrie durch diese Längenänderungen sind die Drehpunkt-Verschiebungen beim Ausschwenken in dafür benutzten Federgelenken überdies nicht merklich beteiligt.
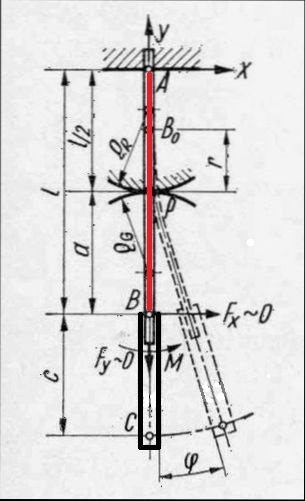
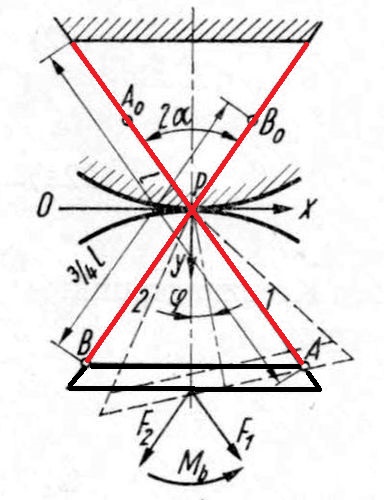 Abb.5 Einblatt-Federgelenk Kreuz-Federgelenk [4]
Abb.5 Einblatt-Federgelenk Kreuz-Federgelenk [4]
Das Einblatt-Federgelenk soll nur mit einer Längskraft belastet werden, damit sich der Drehpunkt nicht zusätzlich verlagert. Theoretischer Vorteil der ausgeschlossenen Querkraft ist, dass der zu untersuchende Balken "reiner Biegung" (konstante Krümmung) unterliegt.
Am "Blauen Wunder" wurde diese einfache Lösung aus Festigkeitsgründen nicht angewendet, sondern für jede Hauptrichtung ein separates Federblatt eingebaut (jedes der beiden Blätter soll nur Längskräften ausgesetzt sein).
Beim Kreuz-Federgelenk können Zugkräfte in beiden Federblättern übertragen werden, so dass es sich auch für das "Blaue Wunder" geeignet hätte. Dass sich der Ort des Drehpunktes gegenüber dem Einblatt-Federgelenk besonders wenig verändert, ist nur bei großen Ausschwenkungen in der Gerätetechnik ein nutzbringender Vorteil (s. oben).
5. Untersuchung eines Zweiblatt-Federgelenks von Claus Köpcke ↑ Anfang
Es handelt sich um den Typ A (Abb.1), an dem ich Modell-Versuche anstellte (siehe auch [1], Abb.9, rechts). Dabei stellte ich fest, dass sich die vertikale Feder (Anmerkung 3) S-förmig, aber nicht punkt-symmetrisch biegt, und dass das für das Ausschwenken erforderliche Drehmoment mehrfach größer ist als beim Weglassen dieser zweiten Feder. Ihre Biegung ist am der der Querfeder nahen Ende größer als am anderen Ende. Diese vorerst tendenziellen Beobachtungen waren der direkte Anlass dafür, mich im vorliegenden Artikel noch einmal damit zu befassen und wenn möglich, eine quantitative Beurteilung (Beschreibung mit Formeln) abzugeben.
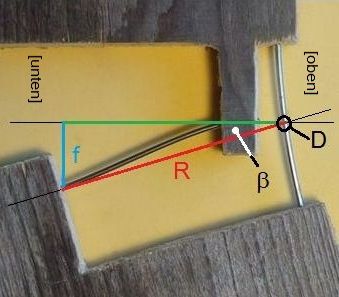 Abb.6 Köpckes "Pylon-Gelenk" A,
Abb.6 Köpckes "Pylon-Gelenk" A,
Modell 1 mit Fahrradspeichen (50mm x ∅2mm)
Als gemeisamen Drehpunkt D der Feder-Zweierkombination lässt sich mit guter Näherung die Mitte der Querfeder annehmen (Abb.6). Der biegsame Teil der mit dieser in gleicher Ebene befindlichen vertikalen Feder beginnt zwar nicht dort, weil Platz für das Einspannen erforderlich ist. Aber die vertikale Feder hat an ihrem oberen Ende doch immer die Richtung durch den Drehpunkt, was die weiteren Überlegungen erleichtert: Die Steifigkeiten der beiden Einzelgelenke aus Quer- bzw. Vertikalfeder lassen sich addieren (die beiden Federn sind "parallel geschaltet").
5.1 vertikale Feder ↑ Anfang
Für die vertikale Feder lässt sich der Fall 26 aus der obigen Liste (Abb.2) anwenden. Die beiden Einspannstellen bleiben zwar nicht ganz parallel, denn das äußere Ende bewegt sich beim Ausschwenken auf einem Kreis um den Drehpunkt D. Aus Fall 26 lässt sich aber ableiten, was Abb.6 zeigt, dass nämlich die Biegelinie S-förmig, nur nicht ganz punkt-symmetrisch ist. Für letzteres ist gerade der Nichterhalt der Parallelität verantwortlich, denn die Feder behält außen nicht ganz die gleiche Richtung wie vorher bzw. nicht wie am oberen Ende. Das wird vorab erhellt, wenn man den Fall 26 als Kombination der Fälle 1 und 2 konstruiert (Abb.5).Fall 1 + Fall 2 = Fall 26
Man denke sich zuächst die vertikale Feder unten nicht eingespannt, sondern nur durch eine am Ende quer wirkende Kraft P verformt (Fall 1). Die Feder wird einseitig gekrümmt gebogen (maximale Krümmung an der Einspannstelle oben, keine Krümmung am freien Ende).
Nun biegt man die derart gebogene Feder (Anmerkung 4) ein zweites Mal, indem man ein Drehmoment M0 an ihrem freien Ende anlegt (Fall 2). Das Drehmoment ist rückdrehend und sei gerade so groß, dass die Tangente am Federende die gleiche Richtung wie am Anfang hat bzw. der an der Einspannstelle parallel gerichtet ist. Das Ergebnis deckt sich mit dem Fall 26, wenn das (über die ganze Federlänge konstant wirkende) Moment M0 = P·l/2 ist (im Fall 1 ist P·l das Moment an der Einspannstelle). Die Feder ist punkt-symmetrisch S-förmig gebogen.
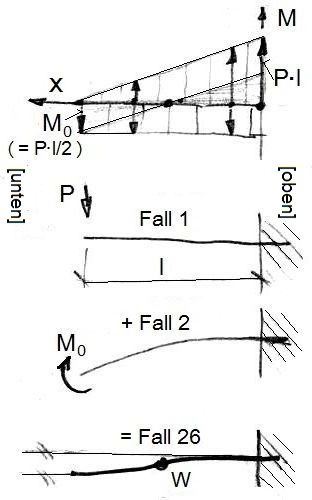
< < Abb.7 Fall 1 + Fall 2 = Fall 26
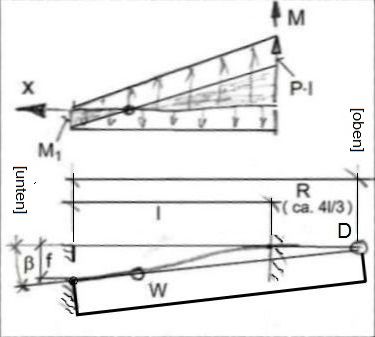 ↑ ↑ Abb.8 Fall 26a (Variante von Fall 26): M(x) = P·(l-x) - M1
↑ ↑ Abb.8 Fall 26a (Variante von Fall 26): M(x) = P·(l-x) - M1
Fall 26a (Variante von Fall 26)
Im untersuchten Fall (Abb.6) ist das rückbiegende Drehmoment M1 kleiner als im Fall 26:M1 < P·l/2.
Es verbleibt eine kleine Unparallelität zwischen den Federenden. Der untere Federteil ist weniger gekrümmt als der obere, und der Wendepunkt W des S liegt näher beim unterenen Ende.
Im Folgenden wird der Fall 26 entsprechend variiert (>> Fall 26a) und dessen Biegelinie nach bekanntem Vorgehen [8] rechnerisch hergeleitet.
Diese Herleitung erfolgt mit M1 als eine noch Unbekannte. Ihre Größe erhält man schließlich aus den Gleichungen für die gefundene Biegelinie der vertikalen Feder, denn deren Neigung am unteren Ende ergibt sich auch aus den geometrischen Zusammenhängen:
tan β ≈ β = f / R (s. Abb.6, Abb.8 und Abb.11).
Die Gleichung M(x) / EJ = w''(x) ist zweimal zu integrieren. Nach der ersten Integration erhält man die Neigung
β(x) = w'(x) und danach die Gleichung der Biegelinie w(x) [8].
E = Elastizitätsmodul des Federstabmaterials; J = Flächenträgheitsmoment des Stabquerschnitts (konstant bei Stäben konstanten Querschnitts).
1. Integration:
w'(x) = ∫ M(x) dx / EJ = ∫ (P (l-x) - M1) dx / EJ= (P (lx - x2/2) - M1x + C1) / EJ
Randbedingung: keine Neigung an der oberen Einspannstelle >> w'(x=0) = 0 >> C1=0 w'(x) = (P (lx - x2/2) - M1x) / EJ . (1)
2. Integration:
w(x) = ∫∫ M(x) dx2 / EJ = ∫ (P (lx - x2/2) - M1x) dx / EJ = (P (lx2/2 - x3/6) - M1x2/2 + C2) / EJ .
Randbedingung: keine Auslenkung an der oberen Einspannstelle >> w(x=0) = 0 >> C2=0 w(x) = (P (lx2/2 - x3/6) - M1x2/2) / EJ . (2)
Bestimmen von M1:
[a] 1. Integration: β = w'(x=l) = (P (l2 - l2/2) - M1l) / EJ
[b] Geometrie: β = w(x=l) / R = f / R ; mit f = w(x=l) = (P (l3/2 - l3/6) - M1l2/2) / EJ (aus 2. Integration) wird :
β = (1/R) (P (l3/2 - l3/6) - M1l2/2) /EJ ; mit R = k·l
β = (1/k) (P (l2/2 - l2/6) - M1l/2) /EJ .
Gleichsetzen ([a] = [b]): P (l2 - l2/2) - M1l = (1/k) (P (l2/2 - l2/6) - M1l/2) >> M1 = Pl (1/2 - 1/(3k)) / (1 - 1/(2k)) . (3)
ausgewählte Werte: mit k= 1 ist M1= Pl/3 ,
mit k=5/4 (wie in 5.3) ist M1= 7·Pl/18 ,
mit k=4/3 (etwa in Abb.6) ist M1= 2·Pl/5 und
mit k= ∞ (wie im Fall 26) ist M1= Pl/2 (= M0) .
Aus Gleichung (2) wird z.B. mit dem ausgewählten Wert
k = 5/4 (wie in 5.3)
w(x) = (P (lx2/2 - x3/6 - 7 lx2/36) / EJ (2a) ,
und die Durchbiegung am rückgebogenen Ende ist
f = w(x=l) = P l3 / (7·EJ) .
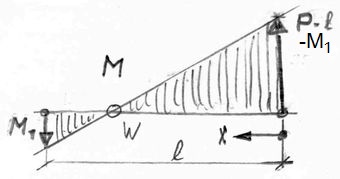
Zum Vergleich: f = P l3 / (12·EJ) im Fall 26. << Abb.9 Momenten-Verlauf M = f(x)
Abb.9 zeigt die Lage des aus der Mitte (Fall 26) in Richtung des zurückgebogenen Endes verschobenen
Wendepunkts W. Seine x-Koordinate ist mit MW=0 und Anwendung des Strahlensatzes bestimmbar.
Bei ebenfalls k=6/5 bzw. M1= 8·Pl/21 beträgt sie: x= 13·l/21 .
5.2 horizontale Feder ↑ Anfang
Die Zusammenhänge in der horizontalen Feder von Köpckes Gelenk A sind in Abb.2 (Fall 2) umfassend dargestellt.
Ihre Belastung ist aber an die der vertikalen Feder, die mit ihr zusammen wirkt, gebunden. Beide Federn müssen bei primären Laständerungen (Verkehrslast- und Temperatur-Änderung) das gegenseitige Drehen der durch sie verbundenen Brückenteile ermöglichen. Ich werde als Modell-Last eine Kraft P auf das untere Ende der vertikalen Feder wirken lassen. Diese ist der horizontalen Feder parallel und belastet diese mit dem über die Länge konstanten Drehmoment P·R (Stichwort: "reine Biegung"; Abstand R: siehe Abb.6, Abb.8 und Abb.11).
5.3 Versuche an einem Modell des Zweiblatt-Federgelenks ↑ Anfang
Das in Abb.6 gezeigte Modell 1 erwies sich für quantitative Anwendung als schlecht geeignet. Die Löcher zur fixen Einspannung der Stäbe weiteten sich bei Belastung deutlich (wurden oval, Stäbe wackelten leicht). Deshalb fertigte ich noch ein Modell 2 aus Hartholz an. Ich machte es auch etwa fünf mal größer, sodass die auftretenden Kräfte wesentlich kleiner und die Verformungen der Holzteile ganz sicher vernachlässigbar sind (Abb.10).

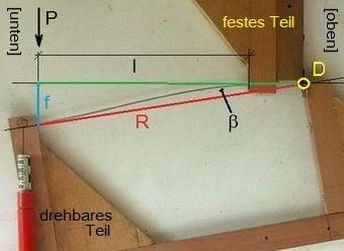 Abb.10 Modell 2 aus Buchenholz für Federstab-Längen bis 300mm
Abb.10 Modell 2 aus Buchenholz für Federstab-Längen bis 300mm
Abb.11 Versuch mit lediglich vertikaler Feder: Fahrradspeiche mit Ø2mm und Länge l= 240mm,
J = 0,7855 N·mm4, EStahl = 2,1·105 N/mm2, k= R/l = 5/4 .
(Scharnier D anstatt horizontaler Feder)
Für das Ausschwenken der vertikalen Feder um β = 10° wurde die Kraft P ≈ 4 N gemessen (Abb.11).
Der theoretische Wert ergibt sich mit der in 5.1 gefundenen Gleichung (1) und dem Wert M1= 7·Pl/18 zu 4,54 N .
Die Rechnungen sind die folgenden:
(1) β = w'(x=l) = (P (l2 - l2/2) - M1l) / EJ ; mit M1= 7·Pl/18 wird:
β = P l2 / (9·EJ) ; nach P umgestellt:
P = tanβ·9·EJ / l2 ; nach dem Einsetzen von β = 10° und der Werte für E und J folgt das Ergebnis:
P = 4,54 N .
Für den Versuch mit horizontaler Feder wählte ich einen Stahlstab mit gleicher freier Länge 240mm wie die der vertikalen Feder, aber mit größerem Durchmesser 4 mm (J = 12,57 mm4), weil sonst eine sehr kleine, kaum messbare Kraft P aufzubringen wäre.
Die Kraft hat denselben Angriffspunkt und dieselbe Richtung wie vorher die Kraft an der vertikalen Feder. Der Hebelarm für das konstante Beiegemoment M0 = P·R ist somit R = 300mm.
Für das Ausschwenken von β = 10° wurde die Kraft P ≈ 5,5 N gemessen.
Der theoretische Wert ergibt sich mit der in der Abb.2 für den Fall 2 angegebenen Gleichung:
β = M0·l / (EJ) ; mit M0 = QP·R wird:
β = P·R·l / (EJ) ; nach P umgestellt:
P= tanβ·EJ / (R·l); nach dem Einsetzen der Werte folgt das Ergebnis:
P = 6,46 N .
Umgerechnet auf denn Stabdurchmesser 2 mm ist P = 0,40 N . Die horizontale Feder ist somit mehr als zehn mal weicher (4,54 / 0,4 ≈ 11) als die vertikale Feder, deren unteres Ende etwa im Mittelpunkt der horizontalen Feder schwenken muss.
6. Ausklang ↑ Anfang
Die Arbeit ließe sich gut und gerne noch fortsetzen. Ich beende sie aber an dieser Stelle. Ich bin ein paar Fragestellungen mit bereits mehr technischem Wissen zu elastischen Verformungen nachgegangen als es Köpke haben konnte. Dabei stellte sich heraus, dass diesen ungewöhnlichen Balken-Kombinationen zu Gelenken mit Fausformeln und Rechnen von Hand, wie ein Jahrhundert nach Köpke bekannt und angewendet, auch etwas näher zu kommen ist. Das sollte genügen. Mit Faustformeln lassen sich solche ungewöhnlichen Federkonstruktionen ohnehin nicht besonders genau und auch nicht besonders anschaulich berechnen. Zudem haben wir mit der Finite-Elemente-Methode längst ein viel genaueres Werkzeug, dessen rezeptartig nötige Anwendung aber leider höchst unanschaulich ist und sich nicht für einen für einen Jedermann-Ingenieur geschriebenen kurzen Artikel eignet (auch nicht für einen Jedermann-Ingenier als Autor).
7. Anmerkungen ↑ Anfang
Anmerkung 1: M und P sind voneinander unabhängige Belastungsgrößen. Die Gleicheit P·l = M0 ist lediglich erforderlich, um die in Abb.3a vorgenommene "Addition" in Abb.2 quantitativ nachvollziebar zu machen.
Anmerkung 2: Ich hätte mich der Gefahr, beim Vergleichen der Fälle, deren Größen nicht einheitlich festgelegt sind, Fehler zu machen, nicht aussetzen müssen, wenn ich die Tabelle in Abb.2 selbst angefertigt hätte. Ich wollte mich aber absichtlich auf eine Literaturquelle stützen und die darin enthaltene umfangreiche Arbeit, die Gleichungen herzuleiten (die dann aber von einheitlicher Festlegung ausgehen !), nicht wiederholen.
Anmerkung 3: In den Darstellungen ab Abb.6 ist die Entsprechung für die in Köpckes Brücken-Gelenk vertikal angeordnete Feder immer horizontal gezeichnet. Das erleichtert die Vergleiche mit den "Fällen" in Abb.2.
Anmerkung 4: Anstatt sich zu merken, dass die Kraft P weiter besteht und im zweiten Schritt im Moment M0 wieder auftaucht, kann es anschaulicher sein, sie als erledigt zu betrachten und mit einer Federform weiter zu arbeiten, die durch die Wirkung der Kraft P enstanden ist.
8. Literatur ↑ Anfang
[1] Siegfried Wetzel: Die Elbe-Brücke "Blaues Wunder",[2] HÜTTE - des Ingenieurs Taschenbuch, theoretische Grundlagen, Ernst & Sohn, 1955 (28. Aufl.), S. 872 bis 891
(insbesondere: Seiten 872 und 884),
[3] DUBBEL - Taschenbuch für den Maschinenbau, Band I, Springer, 1955 (11. Auflage), Seiten 354 bis 363,
[4] Siegfried Hildebrand: Feinmechanische Bauelemente, Hanser 1968, Seiten 429 bis 433,
[5] Hartwig Hasselmeier: Das Kreuzfedergelenk als lose- und reibungsfreies Lagerelement ...,
Jenaer Jahrbuch 1951, Kommissionsverlag Gustav Fischer, Jena, Seiten 240 bis 253,
[6] Hartwig Hasselmeier: Allgemeine Untersuchungen über das Kreuzfedergelenk, Jenaer Jahrbuch 1954,
VEB Gustav Fischer Verlag, Jena, Seiten 280 bis 306,
[7] Werner Lotze: Grundzüge der Kinematik von Biegefederaufhängungen, Wissenschaftliche Zeitschrift der
TU Dresden, 1963, Heft 6 (Vorabdruck aus der 1965 vorgelegten Dissertation des Verfassers),
[8] HÜTTE - des Ingenieurs Taschenbuch, theoretische Grundlagen, Ernst & Sohn, 1955 (28. Auflage), Seite 910,
DUBBEL - Taschenbuch für den Maschinenbau, Band I, Springer, 1955 (11. Auflage), Seite 348.
↑↑ Anfang
<< andere Mechanik-Beiträge
<< Home