<< Home
<< andere Brücken-Beiträge

  ↓↓  Ende

Elbe-Brücke "Blaues Wunder"
Mutmaßungen über die in ihr enthaltenen Feder-Gelenke

Vorbemerkung:
Mit dem Untertitel wird darauf hingewisen, dass diverse technische Details der Brücke nicht öffentlich bekannt bzw. von Personen, die keinen nahen Zugang (auf die Pfeiler und Pylone, unter die Mittelöffnung und in die Ankerkammern) haben, nicht erkennbar sind. Teile der folgenden Darstellungen enthalten deshalb zur Zeit noch zwar plausible, aber von Mutmaßungen nicht ganz freie Überlegungen.

Inhalt

1. Einleitung  ↑ Anfang

Die am Ende des 19. Jahrhunderts zwischen Loschwitz und Blasewitz über die Elbe bei Dresden geplante Brücke sollte keine Hängebrücke sein, denn seit etwa Mitte des Jahrhunderts war diese wegen Windanfälligkeit, die sich in Schwingungen der Fahrbahn äußerte und mehrmals bei Brücken dieser Bauart sogar zum Einsturz geführt hatte, in Verruf gekommen.
Die Elbe-Brücke sollte keine/n Pfeiler im Fluß haben. Die sich daraus ergebende Spannweite von mehr als 140 Metern konnte aber bisher nur bei Hängebrücken erreicht werden, weshalb die Idee verfolgt wurde, eine Hängebrücke derart zu verstärken, dass sie wenig oder nicht windanfällig ist.

Eine Hängebrücke zu verstärken, d.h. letztlich ihre "Schlaffheit" durch Verzicht auf tragende Ketten oder Seile zu eliminieren, bedeutete den Rückgriff auf mehr oder weniger starre Brücken bisheriger Bauart. Diese mussten neuerdings aber nicht mehr einteilig sein. Johann Wilhelm Schwedler hatte den aus zwei starren Bogenteilen bestehenden, statisch bestimmten Dreigelenkbogen erfunden, und damit die Brückenkonstruktion auf theoretisch sicherere Basis gestellt. Den Begriff der statischen Sicherheit hatte Karl Culmann kurz vorher anlässlich seiner einschlägigen theoretischen Vorarbeit geprägt.

Claus Köpcke, der Konstrukteur der Loschwitz-Blasewitz-Brücke, die später den Zunamen Blaues Wunder erhielt, verstärkte/variierte eine Hängebrücke zu einem Bauwerk aus vier sichelförmigen Fachwerkträgern, die zusammen wie eine Hängebrücke aussehen. Das System der untereinander und mit dem Baugrund gelenkig verbundenen vier Teile ist statisch bestimmt.

2. Die Steifigkeit der Hängebrücken  ↑ Anfang

Die Ketten oder Seile einer Hängebrücke sind schlaffe Bauteile. Sie leisten, wenn sie lediglich wie einzeln angebrachte Wäscheleinen benutzt werden, keinen Beitrag zur Steifigkeit einer solchen Brücke. Steif ist allein der Fahrwegbalken. Und da dieser an vielen eng benachbarten Stellen von den Ketten oder Seilen getragen wird, wird er mit geringer Dicke, d.h. nicht besonders steif ausgelegt. Er verformt sich bei wandernder Nutzlast elastisch. Insbesondere sind sowohl durch die sich bewegende Nutzlast, aber mehrheitlich durch den Wind angeregte periodische Verformungen (vertikale und Torsions-Schwingungen) möglich.

Vom Wind verursachte Einstürze bei seit etwa 1800 nicht nur für Fußgänger sondern auch für Fahrzeuge gebauten Hängebrücken wurden zunächst wenig beachtet. Das änderte sich erst ab 1850 als über 200 Menschen beim Einsturz einer Brücke in Frankreich starben (Anmerkung 1).

Der erste Brückenbauer, der gleich mehrere Maßnahmen gegen solche Unfälle schon bei seiner ersten Brücke, der über den Niagara-Fluss (Niagara Falls Suspension Bridge, fertig gestellt 1855, Abb.1), ergriff, war der in die USA ausgewanderte Deutsche Johann August Röbling. Zwischen den Spitzen der Pylone (also von fixen Punkten aus) und den äüßeren Teilen des Fahrbahnträgers brachte er zusätzliche schräge Seile an, damit diese Brückenteile nicht mehr pendeln/schwingen können. Gegen das mögliche Auf-und Abschwingen des Träger-Hauptteiles montierte er in den Flussufern verankerte, von unten haltende Seile .

1854 stürzte auch die 1849 als erste Hängebrücke mit über 300 Metern Spannweite erstellte Wheeling Suspension Bridge über den Ohio-River während eines Sturmes ein. Sie wurde mit gleichem Fahrwegbalken wieder aufgebaut, erhielt aber die von Röbling verwendeten, von den Pylonspitzen ausgehenden zusätzlichen Schräg-Seile. Für zusätzliche, nach unten gegenhaltende Seile liegt der Fahrbanbalken offensichtlich nicht hoch genug, um die Schiffahrt nicht zu stören. Es wurden aber annähernd horizontal liegende zusätzliche Seile zwischen der Fahrbahn und Fix-Punkten an den Ufern eingebaut (Abb.2, auch ein Querseil über die Hängeseile,). Auf diese gegen mögliches horizontales Schwingen gerichtete Maßnahme verzichtete Röbling, auch bei seiner späteren und bekannteren Brücke über den Ost-Fluss zwischen Manhattan und Brooklyn in New York (Brooklyn Bridge).

Abb.1   Hängebrücke über den Niagara-Fluss unterhalb der Niagarafälle,
            [Niagara Falls Suspension Bridge]; untere Seile hervorgehoben

Abb.2  Hängebrücke über den Ohio-Fluss in Wheeling/West-Virginia,
            [Wheeling Suspension Bridge]; einige seitliche Seile hervorgehoben

Die Niagara-Brücke wurde Ende des 19. Jahrhunderts durch eine um sie herum gebaute Bogenbrücke (neuer Name: Whirlpool Rapids Bridge) ersetzt. Die Ohio-Brücke ist ohne wesentliche Änderung bis heute in Gebrauch.

Die Neigung des Fahrbahnträgers, vom Wind zum Schwingen (transversal auf und ab oder in sich tortierend) angeregt zu werden, ist nicht nur von den Hängeseilen, sondern ebenso von der Geometrie seines Querschnitts abhängig. Diese bestimmt einerseits die Wind-Angriffsfläche, anderenseits die Widerstandfähigkeit gegen (elastische) Verformung. Die entsprechenden dynamischen Zusammenhänge wurden erst nach dem Einsturz der Tacoma-Narrows-Brücke 1940 erkannt und beachtet. Die früheren Hängebrücken waren mehr oder weniger unwissentlich diesbezüglich günstiger ausgelegt worden als Letztere (Anmerkung 2), deren Fahrwerkbalken aus Kostengünden wesentlich schlanker war.

3. Köpckes "verstärkte Hängebrücke"  ↑ Anfang

Der erst 30-jährige Köpcke veröffentlichte am Anfang der 1860er-Jahre Überlegungen darüber, wie sich die allgemein bekannt gewordenen, oben genannten Schwächen der Hängebrücken beseitigen ließen [1], [2]. Hauptsächlich suchte er nach Mitteln, mit denen "... Kettenbrücken gegen Oscillationen, namentlich in verticaler Richtung, zu schützen sind, ...", und folgte schließlich der "... Idee, die als Zugleisten konstruierte Kette durch Gitter mit dem Fahrbahnbalken zu verbinden, um eine steife Wand zu erhalten, ... [2]. Eine gar zu steife Struktur wollte er aber nicht schaffen, denn "eine Temperaturerhöhung würde die Folge ... haben, dass ... eine außerhalb der zulässigen Grenzen enstehende Spannung möglicherweise hervorgerufen ..." werden könnte. Mit anderen Worten: Köpcke bemühte sich um eine statisch bestimmte Struktur, nur war ihm dieser Begriff in dieser Zeit noch nicht geläufig.

Eine uns bewegende Frage stellte sich auch Köpcke:
"...ob das Ganze überhaupt noch als Hängebrücke anzusehen ist, ...?" [1].
Eine Antwort gab er auch nicht.

4. Köpckes Dreigelenkbogen  ↑ Anfang

Abb.3   hängender Dreigelenkbogen, Prinzip, [2]

Als statisch bestimmte Struktur propagierte Köpcke einen hängenden Dreigelenkbogen (Abb.3), der später, nachdem Johann Wilhelm Schwedler einen solchen, aber aufrecht stehenden Bogen als Bauart einer Bogenbrücke eingeführt hatte, als auf den Kopf gestellter Dreigelenkbogen bezeichnet wurde (Anmerkung 3).

In Abb.4 hat Köpcke die Umwandlung einer Hängebrücke in einen solchen Dreigelenkbogen (eng schraffierte Bereiche = zwei "steife Wände"; drei Gelenke: A, B und C) prinzipiell dargestellt. In den "Wänden" entstehen weitestgehend nur Zugspannungen. Sie sind auf den Pylonen drehbar gelagert. Der Horizontalzug wird durch in den Ufern verankerte Spannseile von den Pylonen fern gehalten.

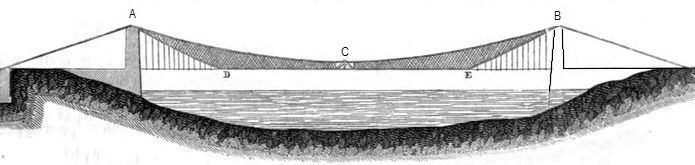
Abb.4   Umwandlung einer Hängebrücke in zwei hängende starre Teilbögen ("starre Wände", eng schraffierte Bereiche);
            zusammen mit zwei äußeren (A, B) und einem beide verbindenden (C) Gelenk/en  =  ein Dreigelenkbogen, [2]

Abb.5   Hängebrücke Kettensteg in Frankfurt/Main aus vier massiven, sichelförmigen Brückenteilen,
            Dreigelenk-Doppel-Mittelfeld (Gelenke A, B und C; A u.B auf Pylonen und horizontal beweglichen Rollen),
            plus je ein Außenfeld (Gelenke A, B und horizontal bewegliche Auflager F, G),
            unter den Zugangstreppen befindliche Anker, über Umlenkketten an F u. G ziehend,
            [Eiserner Steg]

Die Vorarbeit Köpckes an einer wie eine Hängebrücke aussehenden Brücke ("verstärkte Hängebrücke") aus massiven, im Mittelfeld als "Dreigelenkbogen" verbundenen sichelförmigen Brückenteilen wurde mehrmals aufgegriffen. Der 1868 fertig gestellete Kettensteg in Frankfurt/Main (Abb.5, Anmerkung 4, [5]) war eine der ersten nach diesem Prinzip gebauten Brücken.

5. Die sieben Gelenke des Blaues Wunders  ↑ Anfang

Zwischen dem Vorschlag Köpcke's des "auf dem Kopf gestellten (hängenden) Dreigelenkbogens" und dem Bau "seines Blauen Wunders" (Anmerkung 5) waren fast 30 Jahre vergangen.

Abb.6a   "Blaues Wunder" in Dresden, 1894 ohne Pylone erbaut, [Chriusha] .

Inzwischen war er vom Aufhängen einer "versteiften Hängebrücke" an Pylonen (bei A in Abb.5) abgekommen . Er konnte auf die Pylone verzichten, indem er die Brücke mittels Rollenlagern R auf unter der Fahrbahn endende Pfeiler setzte (Abb.6a und Abb.6b). Die oberen Gelenke A und B haben für die Mittelteile nur noch die Funktion, den von diesen verursachten Horizontalzug über die Obergurte der Seitenteile zu den "Anker-Gelenken" F und G an den Ufern weiter zu leiten. Zu den drei Gelenken des hängenden Dreigelenkbogens kamen die Rollenlager R_L und R_R hinzu. Da das Blaue Wunder auch außerhalb der (Pseudo-)Pylone eine "verteifte Hängebrücke" ist, sind auch die "Anker-Gelenke" mitzuzählen, woraus sich die Gelenke-Geamtzahl von drei über fünf auf sieben erhöht.

Das mittlere Gelenk C wird nur vom Horizontalzug belastet. Bei unterschiedlicher Verkehrslast auf den beiden inneren Brückenteilen kommt dort eine kleine vertikale Kraft hinzu.

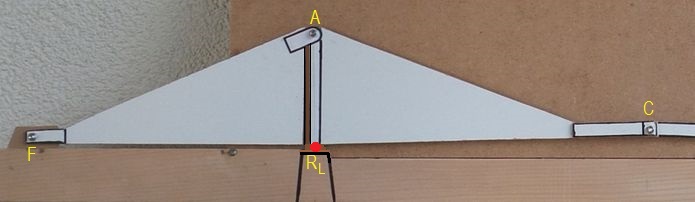
Abb.6b   Modell des Blauen Wunders mit sieben Gelenken (Darstellung der linken Brücke-Hälfte mit vier Gelenken)
            A (B):    oberes Gelenk (Drehgelenk, "Pylon-Gelenk")
            R_L (R_R): Rollenlager (Dreh- und Schiebe-Gelenk)
            C:         mittleres Gelenk (Drehgelenk, "Scheitel-Gelenk")
            F (G):    äußeres Gelenk (Drehgelenk, "Anker-Gelenk")

Über A (B) wird auch der größere Teil der Gewichtskraft des Seitenteils auf das benachbarte Mittelteil abgestützt. Dafür ist dessen darunter befindliche Kante verstärkt (Anmerkung 6). Der kleinere Teil des Seitenteil-Gewichtes wird über F (G) in den Baugrund geleitet.

Das "Anker-Gelenk" F (G) ist Teil des Baugrundes, denn die Anker-Masse ist so schwer, dass sie in allen Betriebs-Fällen auf dem Baugrund ruht (Anmerkung 7).

6. Die statische Bestimmtheit des Blaues Wunders  ↑ Anfang

Köpcke benutzte auch am Ende der 1880er-Jahre, als der Bau des Blauen Wunders nach seinem Entwurf kurz bevorstand, in seinen Veröffentlichungen noch nicht den Begriff der statischen Bestimmtheit, sondern empfahl die Anwendung dieses allgemeinen Prinzips, indem er einige seiner Vorteile wie "die genaue Bestimmbarkeit der Inanspruchnahmen und der Ausschluss schädlicher Wirkungen der Temperaturwechsel" aufzählte [3].
Lediglich in den neun Bedingungen, die die Königliche Wasserbaudirektion unter dem Vorsitz von Köpcke für den Bau der Brücke bereits gestellt hatte, wird man fündig: "7. Für die drei Hauptöffnungen sind statisch bestimmte Eisenkonstruktionen zu wählen." [5]

Überprüfung der statischen Bestimmtheit:
Die Überprüfung ist schnell und einfach mit einem in der Statik gebräuchlichen Abzählkriterium möglich. Für ebene Systeme lautet es:
n = a + z - 3 · t = 0.
n ist der Grad der Beweglichkeit, der bei einem statischen System Null
   (unbeweglich im Vergleich zu Mechanismen) zu sein hat.
t ist die Zahl der im System enthaltenen Bauteile
   (im vorliegenden Fall vier aus jeweils einem Fahrbahnbalken, zwei seitlichen Fachwerkwänden
   und einigen teilweise oben angebrachten Querstäben bestehende starre "Röhren").
a ist die Zahl der in allen Auflagern horizontal und vertikal übertragbaren Kräfte
   (im vorliegenden Fall 2 in den Rollenlagern R und 4 in den "Anker"-Gelenken F und G (Anmerkung 8).
z ist die Zahl der in den Zwischenglenken horizontal und vertikal übertragbaren Kräfte
   (im vorliegenden Fall je 2 in den Gelenken A, B und C).
Die Auswertung ergibt wie erwartet statische Bestimmtheit (n=0; Anmerkung 9):
n = 6 + 6 - 12 = 0.

7. Köpckes Feder-Gelenke  ↑ Anfang

Die Verbindung der mit starren Wänden versehenen Brücke durch Gelenke war von Anfang an Teil der von Köpcke erdachten „versteiften 3-gelenkigen Hängebrücke“. Über die Art der Gelenke äußerte er sich aber erst kurz vor dem Bau des Blauen Wunders [4].

Die in der Zwischenzeit in einigen neu enstandenen Brücken benutzten Bolzengelenke verwarf er aus zwei Gründen. Die Bolzen würden bei künftigen großen Brücken zu dick und wären nicht sicher mit den Brückenträgern zu verbinden. Zudem befürchtete er, dass diese bei den kleinen erforderlichen Verdrehungen gar nicht "ansprechen" (die Haftreibung nicht überwinden) würden.

Heinrich Gottfried Gerber hatte inzwischen an Stellen mit vorgesehener Gelenkigkeit offensichtlich einen Fachwerk-Gerberträger biegeweich gestaltet, und Köpcke münzte diese Lösung jetzt dezitiert in den Begriff und das Bauelement "Federgelenk" um. Als Vorbild diente ihm das an einer Blattfeder aufgehängte Pendel einer Turmuhr.

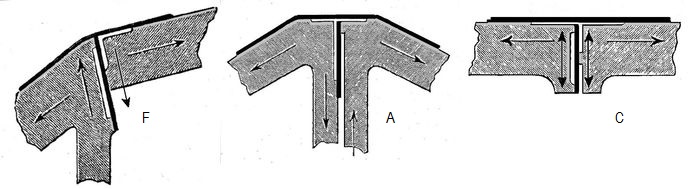
Abb.7  Blattfeder-Gelenke nach Köpcke für "versteifte 3-gelenkige Hängebrücke",
           Bauart Blaues Wunder; [4]
           links:   "Anker-Gelenk"    F   (vertikale Doppelpfeile in Einfachpfeile geändert)
           mittig:  "Pylon-Gelenk"    A
           rechts: "Scheitel-Gelenk" C

In den Prinzip-Darstellungen der Gelenke in Abb.7 ist bereits der beim Blauen Wunder vorgenommene Verzicht auf echte Pylone enthalten: Als vertikale Kraft tritt beim "Pylon-Gelenk" A nur die Gewichtskraft des links zu denkenden Brücken-Außenteils auf.

Abb.8  Blattfeder-Gelenk mit gekreuzten Federn ("Kreuzfeder-Gelenk"),
            Feinwerktechnik-Prototyp; Besonderheit: gelochte Feder "umgreift" die andere

Die einfache Blattfeder (wie am Uhrenpendel) ist für die Übertragung von Zugkräften in Blattrichtung gut geeignet. Bei zusätzlichen Kräften senkrecht zur Blattebene entstehen neben Zug- auch Schubspannungen in ihr, und sie nimmt beim Auslenken keine einfache Bogenform an.

Köpke versuchte, "klare Verhälnisse" zu schaffen, indem er jeweils zwei unter 90° gegeneinanander verdrehte (je eine für die Krafthauptrichtungen in der Ebene) Federn pro Gelenk-Stelle vorsah. Den heutigen Stand der Technik in Form eines Kreuzfeder-Gelenkes (Abb.8) verpasste er allerdings, denn seine Federn bilden nicht einen gemeinsamen Kreuzungspunkt, sondern sind voneinander getrennt angeordnet (Anmerkung 10). In dieser Konstellation nehmen insbesondere die vertikalen Federblätter beim Auslenken nicht einfache Bogenform (Abb.9, links), sondern S-Form an (Abb.9, rechts). Sie müssen sich wegen der Distanz vom momentanen Drehpunkt, der sich auf dem oder in der Nähe vom horizontalen Blatt befindet, stärker verformen als die in gekreuzter Anordnung (momentaner Drehpunkt fast im Kreuzungspunkt beider Federn). Zudem sind die vertikalen Blätter der Gelenke F und C je an drei Stellen mit den Festteilen verbunden, was ihre Biegsamkeit mindert.

Abb.9  Feder-Gelenk-Modelle mit Fahrradspeichen (Durchmesser 2 mm, Länge 50 mm, Schwenkung 16°)
           links: Kreuzfeder-Gelenk,
           rechts: Köpckes "Pylon-Gelenk" A

Da die Schwenkungen in den Brücken-Gelenken wesentlich kleiner sind als in den im Maschinen- und Gerätebau verwendeten Kreuz-Feder-Gelenken (< 1° gegenüber > 10°), besteht kein Anlass für die Annahme, dass die im Vergleich zum Kreuzfedergelenk relativ steiferen und nicht optimal konstruierten Feder-Gelenke von Köpcke im Blauen Wunder grundsätzlich Schwachstellen wären. Eine Ausnahme bildet allerdings das Scheitel-Gelenk. C. Dieses ist anders, bzw. wesentlich ungünstiger als in Abb.7 gestaltet. Es wird im folgenden Abschnitt besprochen.

Die Gelenke F und A wurden wahrscheinlich wie in Abb.7 dargestellt ausgeführt. Denkbar ist auch, dass beide Male die Form A verwendet wurde, weil die Belastungsverhältnisse gleich sind: auch bei F nur Gewichtskraft nach (schräg) unten (siehe Klammervermerk in Abb.7). In einer gesonderten Arbeit habe ich die Biegungen der in Abb.9, rechts dargestellten Anordnung theoretisch untersucht und Versuche an einem verbesserten Modell vorgenommen. Mit dem vorliegenden, recht primitiven Modell konnte ich sicher nur feststellen, dass sich die Steifigkeit des Gelenkes durch Zufügen der senkrechten Feder um eine ganze Größenordnung erhöht.

8. Köpckes Feder-Gelenk in Brückenmitte des Blauen Wunders   ↑ Anfang
    (Mutmaßungen)

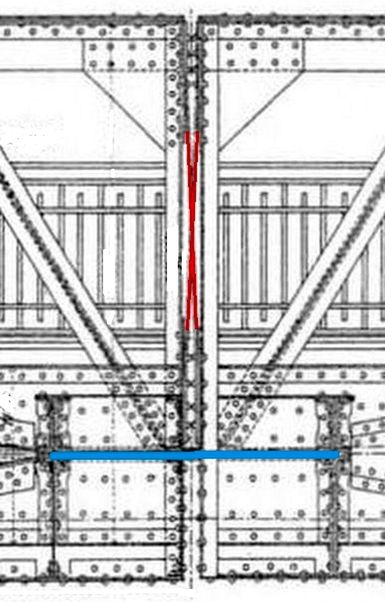
Abb.10   Scheitel-Gelenk (Draufsicht)
              links: vermutlich originale Konstruktionszeichnung; [6]
                       oben (rot):    annähernd vertikale, schleifend gekreuzte Federbätter
                       unten (blau): eins der horizontalen Federblätter
              rechts: aktuelles Foto der annähernd vertikalen, schleifend gekreuzten Federblätter (Seite stromauf, [6])
                         Beide Blätter sind doppelt: Die rot gezeichneten befinden sich nebeneinander (im Bild hintereinander),
                         die blauen aufeinander und in der Lücke zwischen den roten.
                         grün: eins der in den 1980/90er-Jahren eingebauten oberen "Spannglieder" (siehe Abb.12)

Köpckes grundsätzliche Überlegungen beim Scheitel-Gelenk sind bekannt (Anmerkung 11): Wegen einseitiger Verkehrslast (je nachdem, welche Brückenhälfte stärker belastet ist) entsteht in ihm eine vertikale Kraft mit wechselndem Vorzeichen. Der Fall mit Druckkraft in einem Federblatt war wegen der Gefahr des Ausknickens zu vermeiden. Deshalb benutzte er anstatt einer hier zwei annähernd vertikale, schleifend gekreuzte Federbätter (rot in Abb.10, links, oben). Sie sind zwischen den an den in Brückenmitte erhöht ausgeführten Brückenrändern, d.h. über den horizontalen Federblättern (blau) angebracht.

Abb.11   Feder-Gelenk-Modell mit drei sich in einem Punkt kreu-
              zenden Stab-Federn (Fahrradspeichen),
              ausgeschwenkter Zustand

Was zu vermeiden war, ist aber eingetreten: Das von rechts oben nach links unten führende (verdoppelte) Federblatt ist ausgeknickt (blau in Abb.10, rechts). Verantwortlich dafür ist aber gar nicht eine mit der Verkehrslast in Zusammenhang stehende Knicklast (eine der beiden Federn übernimmt die Verkehrslast immer als Zugkraft). Plausibel ist hingegen, dass die Anordnung der vertikalen Federblätter getrennt von den horizontalen für das Knicken verantwortlich ist. Beim Absenken der Brückenmitte (momentane Drehachse (in oder in Nähe der horizontalen Federblätter) nähern sich die vertikalen Federblätter einander, wobei sie wegen des entstehenden Längs-Drucks ausknicken.

Dieses Handicap kann nicht eintreten, wenn sich alle Federn in einem gemeinsamen Punkt schneiden (Abb.11). Es können auch mehr als drei und die Winkel zwischen ihnen beliebig groß sein. Nötig ist auch nicht, dass alle Federn gleich lang und gleich dick sind. Weil die vertikalen Lasten in Brückenmitte des Blauen Wunders relativ klein sind, wäre die Verwendung von zwei kürzeren und dünneren schrägen Federblättern möglich. Die horizontalen Blätter blieben an ihrem Platz, und die sie mittig kreuzenden kurzen schrägen Blätter würden nicht unten überstehen und die Durchfahrthöhe nicht verkleinern.

9. Die Veränderung des Mitten-Gelenks des Blauen Wunders
    in den 1980/90er Jahren  ↑ Anfang

Anfang der 1980er Jahre zeigten sich "... Verschleißerscheinungen, die beim weiteren Ignorieren bestandsgefährdende Folgen heraufbesschworen hätten."; [8]. Der Straßenbahnbetrieb über die Brücke wurde sofort eingestellt, und auch nach den anschließenden Sanierungsmaßnahmen und bis heute nicht mehr aufgenommen. Als vor allem durch Schwingungen in der Vergangenheit überbeanspruchtes Bauglied wurde insbesondere das Scheitel-Gelenk beurteilt und nachgerüstet ("Verstärkung der "Horizontalfedern" ... durch Einbau von 2x4 Spanngliedern [pro Seite]... "); [8].

Diese Veränderung bleibt unverständlich. Die damalige Meinung, dass das Federgelenk in Brückenmitte eine Fehlkonstruktion sei (Anmerkung 12), wäre nachvollziehbar (s.o.); nur, die zusätzlichen horizontalen Spannglieder (Zugstangen) ändern daran nichts. Im Gegenteil: Sie sind verschlimmbessernd. Köpcke hatte schon die Vielzahl der horizontalen Federblätter nicht ganz in einer gemeinsamen horizontalen Ebene anbringen lassen. Außen befinden sich jeweils vier, daneben je zwei Blätter übereinander (siehe Abb.12). Die jetzt hinzugekommenen horizontalen Federn (je zwei "Zugstangen" weit über bzw. unter den Blattfedern) bilden zusätzliche und besonders hohe und somit biegsteife Parallelogramm-Strukturen (Anmerkung 13).

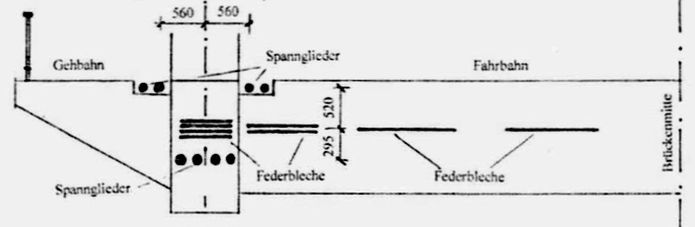
Abb.12   Querschnitt durch das Scheitel-Gelenk; [7]
             (nicht dargestellter oberer Teil: siehe Abb.10; Spannglieder erst in den 1980er-Jahren zugefügt)

Eine überschlägige Rechnung (Abb.13) zeigt, dass für die Übertragung der horizontalen Zugkraft in Brückenmitte gar keine Verstärkung erforderlich gewesen wäre.
Eine der inneren Brückenhälften (Länge etwa 73 Meter, Höhe etwa 24 Meter) ist etwa 750 Tonnen schwer. Ihr Schwerpunkt liege etwa 29 Meter (etwas mehr als bei 1/3 der Länge, denn die Fahrbahn ist gewichtiger als die beiden dreieckigen Wände) vom Rollenlager R_L entfernt. Bei dem Höhen-/Längen-Verhältnis von etwa 2/5 hält eine über das benachbarte äußere Brückenteil beim Pylon-Gelenk A eigeprägte Horizontal-Kraft von 9·10⁶ N das Momenten-Gleichgewicht beim Rollenlager.
7,5·10⁶ N · 29 m / 24 m ≈ 9·10⁶ N.
Das horizontale Kraft-Gleichgewicht ist zusammen mit der über das Scheitel-Gelenk C geführten gleichartigen und gleich großen, aber entgegengesetzt wirkendnen Kraft in der anderen Brückenhälfte erfüllt.

Abb.13   Momenten- und Horizontalkraft-
             Gleichgewicht an einer inneren
             Brückenhälfte

Mit der Annahme, dass die 16 Stück horizontaler Federbätter im Scheitelgelenk 20 mm dick sind und einer Zugspannung von 200 N / mm² unterworfen werden dürfen, so brauchten sie zusammen nur etwa 2,25 m breit sein.
Tatsächlich haben sie zusammen fast die 3½ -fache Breite (7¾ m). Die damals festgestellte Querschnittsschwächung durch Rost in der Größenordnung von 10% ([7]) rechtfertigte somit nicht den Einbau der Zugstangen.

10. Anmerkungen  ↑ Anfang

Anmerkung 1:
Es handelte sich um die Hängebrücke von Angers. Sie stürzte ein, als Soldaten vorsorglichtlich nicht im Gleichschritt, sondern "ohne Tritt", aber während eines Sturmes über sie liefen (und dabei in Panik gerieten). Das Versagen der Brücke war aber auch durch Korrosionen an den Tragseilen mit verursacht. Trotzdem durften lange Zeit keine Hängebrücken mehr in Frankreich gebaut werden.

Anmerkung 2:
So hatte z.B. Röblings Niagara-Brücke einen relativ steifen Doppel-Fahrbahnträger.

Anmerkung 3:
Eine frühe schmiedeeiserne Bogenbrücke mit Dreigelenkbögen war die 1865 erbaute Unterspreebrücke in Berlin. 1888 wurde sie durch eine gemauerte Bogenbrücke ersetzt, und wird seitdem Moltkebrücke ganannt.

Anmerkung4:
Der Kettensteg / Eiserne Steg wurde 1912 abgetragen und als Auslegerbrücke mit Einhängeträger (Gerberbrücke) ohne Pylone, aber mit dem bisherigen äußeren Erscheinungsbild neu errichtet. Die äußeren Brückenteile sind nicht groß und nicht schwer genug für die Gewichte der relativ langen Auskragungen und des Einhängeträgers. Sie sind deshalb unter den Zugangstreppen verankert. Die Anker halten die äußeren Brückenteile an ihren Enden bei F und G gegen Kräfte nach oben, die von den Gewichten der inneren Brückenteile verursacht sind.

Anmerkung 5:
Köpcke betimmte als Vorsitzender der königlich-sächsischen Wasserbaudirektion mehr oder weniger alle Anforderungen an die neue Brücke selbst und setzte auf diese Weise "sein Brücken-Projekt" durch.

Anmerkung 6:
In diese Verstärkungen in Form rechteckiger Rohre wurden Wendeltreppen eingebaut, wodurch die Illusion zweier Pylone über jedem Pfeiler erhalten blieb.

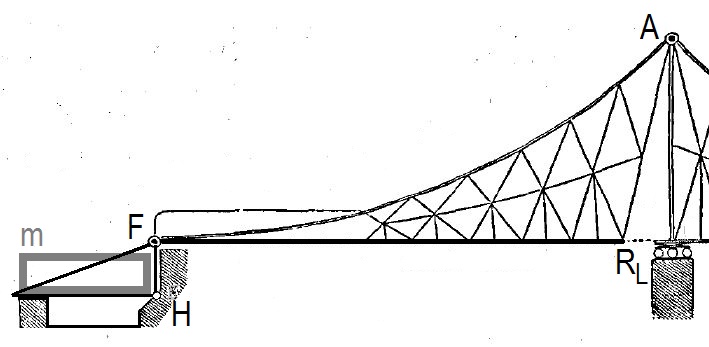Anmerkung 7:
Zwischen Anker-Masse m und Anker-Gelenk F (G) befindet sich ein zweiarmiger Hebel in Form eines Dreiecks, der lediglich die am Anker-Gelenk wirkende fast horizontale Brücken-Zugkraft in eine an der Anker-Masse vertikal ziehende Kraft umzuwandeln hat (siehe nebenstehende Abbildung; [3]). F ist am Ende des senkrechten Hebelarms angebracht, so dass die aus dem Seitenteil der Brücke stammende Gewichtskraft an der Stützstelle H des Hebels unverändert in den Baugrund weiter geleitet wird.

Anmerkung 8:
Die "Anker"-Gelenke F und G werden hier traditionell als Auflager bezeichnet, da sie quasi die Außenteile der Brücke mit dem Baugrund verbinden.
An den beiden Brückenseiten befinden sich jeweils identische Auflager und Gelenke. Weil die Brücke als ebenes statischs System betrachtet wird, sind die Auflager und Gelenke beim Überprüfen der statischen Bestimmtheit aber nur einmal zu zählen.

Anmerkung 9:
n ≤ 0 bedeutet Unbestimmtheit (das System unterliegt Zwängungen).
n > 0 bedeutet Beweglichkeit (bei statischen Systemen irrelevant; bei Mechanismen i.d.R. n = 1).

Anmerkung 10:
Allerdings - möglicherweise unwissentlich - kam er der Kreuzfeder-Gelenk-Lösung im oberen Teil des Scheitel-Gelenks nahe
(rot in rechts wiederholt gezeigter Abb.10).

Anmerkung 11:
"... unter Umständen würde man lieber die [vertikalen] Federn doppelt anbringen, um den... Zweck, die Vermeidung von Druckbeanspruchung, zu erreichen." [4].

Anmerkung 12:
Bei den Bau-Beprechungen für die in den 1980er-Jahren vorgenommenen Verstärkungen des Scheitel-Gelenkes wurde dieses " ... als Fehlkonstruktion beurteilt" (Mitteilung eines damals anwesenden Zuhörers (siehe unter "Weitere Geschichte bis 1990")).

Anmerkung 13:
Zum Vergleich: Bei einem Parallelkurbelgetriebe bleiben die gegenüber liegenden Glieder immer parallel. Sie schwenken nicht gegenseitig aus.

11. Literatur  ↑ Anfang

Nachbemerkung:
Die in den 1980/90er-Jahren am Blauen Wunder vorgenommenen Sanierungen hatten provisorischen Charakter. Die Brücke sollte über kurz oder lang abgebrochen und durch einen Neubau ersetzt werden (Quelle: s. Anmerkung 12). Inzwischen möchte man sie offensichtlich ohne Scheu vor allfälligen hohen Kosten für immer behalten. Es bleibt zu hoffen, dass die zahlende Öffentlichkeit anlässlich der bevorstehenden Baumaßnahmen auch viele technische, sowohl bisherige als auch neu entstehende, Details erfährt, so dass der in diesem Bericht enthaltene Anteil an Mutmaßungen überprüfbar wird und - wenn notwendig - korrigiert werden kann.