<< Home Alternativen zum Gregorianischen Kalendergedruckt in DGC-Mitteilungen #114, Sommer 2008meine Wikipedia-Arbeit, eine Auswahl: Mädler-Kalender Orthodoxer Kalender Ich habe viele Wikipedia-Artikel aus mehreren Wissensgebieten be- oder überarbeitet, einige auch vollständig. Wegen der Fülle der Artikel stelle ich mein Wissen und meine Auffassung oft nur in deren Einleitungen dar, überarbeite diese in der Regel aber vollständig. Die Links führen meistens direkt zur jeweils letzten Artikelversion, die durch meine Arbeit entstand. Ich verweise bewusst nicht auf die aktuelle Version, weil in ihr meine Arbeit wieder verloren gegangen sein kann. ZusammenfassungDurch die Gregorianische Reform wurde unser Kalender wieder mit dem in den Jahreszeiten erkennbaren astronomischen Jahr synchronisiert. Die seitdem gültige Schalt-Regelung garantiert, dass das Kalender-Jahr praktisch nicht mehr abdriften kann. Also war die Reform ziemlich perfekt, wurde aber schon damals [1] und wird auch heute noch gelegentlich [2,3] -leider allzu pauschal- kritisiert. Oft geht es dabei auch nur um Einzelheiten, die die Allgemeinheit nicht berühren, sie deshalb auch nicht interessieren.Als Laie stellt man aber vielleicht doch zum Beispiel fest, dass der Frühlings-Anfang kein fixer Kalendertag ist, sondern zwischen wenigstens drei März-Tagen (21., 20. und 19.3.) pendelt. Bei der Beschäftigung mit den Schalt-Jahren könnte man sich über ihre Verteilung, die zu dem sehr langen 400-jährigen Schaltzyklus führt, wundern. Und wer sich für die Festlegung des Oster-Datums interessiert, mag auf die damit verbundene Kompliziertheit stossen und enttäuscht sein, dass er die Sache nicht versteht. Diese und andere Einzelheiten werden diskutiert, und es wird gezeigt, wie konsequentere -aber in den Sternen stehende- Kalender aussehen. Inhalt1. Vom Julianischen zum Gregorianischen Kalender2. Der Khayam-Zyklus 3. Der Matzka-Zyklus 4. Der Mädler-Zyklus 5. Übersicht auf verschiedene Kalender-Zyklen 6. Ostern als bewegliches Kalender-Datum 7. Die Oster-Rechnung bis zur Kalender-Reform 8. Oster-Rechnung seit der Kalender-Reform 9. Die Oster-Rechnung in den alternativen Kalendern 10. Kritik an der Praxis der Oster-Rechnung 11. Literatur 12. Anmerkungen 13. Nachtrag (2011): Der Milankovic-Zyklus 1. Vom Julianischen zum Gregorianischen Kalender ↑ AnfangDas astronomische (tropische) Jahr ist im Mittel 365,2422 Jahre lang. Die Einschaltung eines Zusatz-Tages im olympischen Rhythmus von 4 Jahren in das sonst 365 Tage lange Jahr führte zum Julianischen Kalender-Jahr mit im Mittel 365,25 Tagen. Durch Wegfall von 3 Schalt-Tagen anlässlich von 3 Jahrhundert-Wechseln in 400 Jahren kommt das durchschnittliche Gregorianische Kalender-Jahr auf 365,2425 Tage. Es ist 25 mal genauer als das Julianische. Nachteilig ist aber, dass sich die Regelung über einen 100 mal längeren Zeitraum erstreckt, der für den Einzelnen unerlebbar und damit unüberschaubar ist.
Eine Graphik von Walter Puschart [4] (Abb.1) erstreckt sich über ca. 1½ Zyklen (600 Jahre) im Gregorianischen Kalender und zeigt das Wandern des astronomischen Frühlingsbeginns zwischen dem 21. und 19. März. Der im Kalender verbliebene Fehler summiert sich in ca. 3320 Jahren zu einen Tag, so dass der Frühlingsbeginn bis zum 18.März (s.Abb.2) vorrücken wird, bevor eine Korrektur des Kalenders durch Auslassen einer Schaltung angezeigt wäre.
Im Nebenbild von Abb.2 ist gezeigt, dass das Fehlerband noch etwas breiter ist, wenn man nicht nur den Frühlingsbeginn betrachtet (Anmerkung 1). Die vordergründige Einfachheit der Gregorianischen Regelung (weiterhin 4-Jahres-Periode, ergänzt durch 3 Säkularjahr-Ausfälle) schneidet in einem von Heinz Zemanek [3] formulierten Mangelwert entsprechend schlecht ab. Zemanek multipliziert die Ungenauigkeit des Kalender-Jahres mit der Zyklus-Länge (beides in Tagen) und findet für den Gregorianischen Kalender einen ca. 4 mal höheren Wert als für den Julianischen (44,0 gegenüber 11,4). Die grosse Zykluslänge von 400 Jahren ist dadurch bedingt, dass die Gregorianischen Reformer entschieden, alle (auch die für die Osterrechnung nötigen) gegenüber dem Julianischen Kalender laufend anzuwendenden Korrekturen ausschliesslich in Säkularjahren vorzunehmen (Anmerkung 2). 2. Der Khayam-Zyklus ↑ AnfangDem bereits im 12. und 13. Jahrhundert lebenden Iranischen Dichter und Mathematiker Omar Khayam wird ein Kalender-Zyklus mit nur 33 Jahren Länge zugerechnet, der sich im Iranischen Kalender bis heute erhalten hat [5]). In ihm sind 7 Schalttage nach je 4 Jahren und 1 Schalttag im abschliessenden 33. Jahr enthalten (Anmerkung 3), 7 üblichen 4-Jahres-Perioden folgt eine davon abweichende 5-Jahres-Periode. Das ergibt für die Länge des hier so genannten Khayam-Jahres 365,242424 Tage, das somit etwas genauer als das Gregorianische ist. Die Ungenauigkeit summiert sich erst in ca.4.440 Jahren auf einen ganzen Tag zuviel (Gregorianisch nach ca. 3.320 Jahren 1 Tag zuviel). Der Hauptvorteil ist aber die Zyklus-Kürze und dass, wie in Abb.3 ist gezeigt, der Frühlingsbeginn-Tag während eines Zyklus' innerhalb eines Kalender-Tages untergebracht werden kann. Zusammen mit der sich langsam einstellenden Verfrühung durch den allgemeinen Fehler bliebe die Bandbreite auf 2 Tage begrenzt, wenn man sich für 1 ausfallenden Schalt-Tag nach ca.4.440 Jahren entschlösse.
Der Mangelwert nach Zemanek (s.o.) verringert sich auf 2,7. 3. Der Matzka-Zyklus ↑ AnfangDer böhmische Mathematiker Wilhelm Matzka schlug 1880 [6], also lange nach der Gregorianischen Reform, einen Kalender mit einer Zyklus-Dauer von 62 Jahren vor. Darin sind 15 Schalttage enthalten. Nach 7 oder 8 olympischen Schalt-Perioden à 4 Jahre wird erst nach dem 5. Jahr erneut geschaltet. Dann folgt der zweite Teil des Zyklus mit 8 oder 7 olympischen Schalt-Perioden und erneuter Schalt-Verzögerung bis zum Ende des Zyklus'. Das Matzka-Jahr ist 365,241936 Tage lang, ist also ein zu kurzes Kalender-Jahr. Man müsste nach ca. 3.795 Jahren einen zusätzlichen Schalt-Tag einfügen.
Der Mangelwert nach Zemanek (s.o.) ist wegen des gegenüber Khayam fast doppelt langen Zyklus' mit 6,0 auch ca. doppelt so gross. 4. Der Mädler-Zyklus ↑ AnfangDer deutsche Astronom Johann Heinrich Mädler war vom russischen Zar aufgerufen, Vorschläge für die Erneuerung des damals in Russland angewendeten Julianischen Kalenders zu machen [7]. Er war nicht mit dem Gregorianischen Zyklus einverstanden und propagierte den vermutlich alt-bekannten 128-Jahre-Zyklus im Jahre 1865 [8]. Er enthält 31 Schalt-Tage. Das Mädler-Jahr ist äusserst genau: 365,2421875 Tage, also nur ganz wenig zu kurz. Erst nach ca. 87.000 Jahren wäre ein zusätzlicher Schalt-Tag fällig. Dieser Zyklus ist eine Folge von 3 Khayam-Zyklen und 1 noch kürzeren Zyklus mit dem schon besprochenen Vorteil, dass der Frühlingsbeginn - hier sogar eine sehr lange Zeit lang - immer der gleiche März-Tag ist. 3 Teil-Zyklen sind je 33 Jahre Lang (je 8 Schaltungen), der 4. Teil hat 29 Jahre (7 Schaltungen): Abb.5.
Der Mangelwert nach Zemanek (s.o.) ist trotz nochmals verdoppelter Zyklus-Länge wegen der hohen Genauigkeit äusserst klein: 0,54. 5. Übersicht auf verschiedene Kalender-Zyklen ↑ Anfang
Zyklus-Name Z-Länge Z-Länge Jahr-Länge J-Lä-Fehler Mangelwert Service n. Band-Breite
Jahre Tage Tage Tage Tage·Tage .. Jahren Tage
julianisch 4 1'461 365,25 0,0078 11,4
gregorianisch 400 146'079 365,2425 0,0003 43,7 3'200 4
Khayam 33 12'053 365,242424 0,000224 2,7 4'422 2
Matzka 62 22'645 365,241936 -0,000264 -5,8 3'782 2(3)
Mädler 128 46'751 365,2421875 -0,0000125 -0,58 86'912 2(3)
Der "Service" (Schalt-Tag auslassen oder einfügen) ist nach einem ganzzahligen Vielfachen der Zyklus-Länge angegeben. 6. Ostern als bewegliches Kalender-Datum ↑ AnfangDer Frühlingsbeginn hat im Kirchenjahr keine direkte Bedeutung, wohl aber das von ihm abhängige Osterfest. Deshalb war die Oster-Rechnung der eigentliche Anlass zur Gregorianischen Reform. Die Festlegung von Ostern interessiert immer noch, auch wenn Ostern und die anderen davon abhängigen christliche Festtage heute oft nur als bewegliche arbeitsfreie Zeit wahrgenommen werden. Vor der Reform war der tatsächliche Frühlingsbeginn dem kalendarischen Ereignis ca. 10 Tage voraus. Im Gregorianischen Kalender wurde die Gleichheit zwischen Kalender und kosmischen Ereignis wieder hergestellt und dafür gesorgt, dass eine prinzipiell nicht zu vermeidende Abweichung zwischen beiden künftig klein bleibt. Für die Oster-Rechnung wird wie bisher für den Frühlingsbeginn vereinfachend der 21. März angesetzt. Um diesen Tag pendelt der tatsächliche Termin künftig nur geringfügig (was bei den angeführten Alternativen besser als im Gregorianischen Kalender ist), er driftet nicht mehr entscheidend ab, wie das im Julianischen Kalender der Fall war. Das Ostern schliesslich entscheidende Ereignis ist der Termin des ersten Vollmondes nach Frühlingsbeginn (Frühlings-Vollmond). Wäre Ostern allein auf den Frühlingsbeginn bezogen, so hätte es wie jeder andere Tag im Jahr, z.B. der Geburtstag eines Menschen, im besonderen der Weihnachtstag als (nachträglich angenommener) Geburtstag von Jesus Christus einen fixen Termin. Die christliche Religion entnimmt aber den Auferstehungstag Christus' dem damals auch für Christen in Jerusalem gültigen jüdischen Kalender. Somit ist ihr Kalender ebenfalls eine Kombination von Sonnen- und Mondkalender, denn der Ostersonntag folgt heute wie damals dem jährlich wechselnden Frühlingsvollmond. Nur ist aus dem historischen ab dem Vollmond-Tag (gleich 14. Nisan und Vortag zum jüdischen Pessah-Fest ) gezählten dritten Tag für die Auferstehung heute der zweite bis achte Tag (1_bis_7_Tage_danach) für Ostersonntag geworden. Der historische Auferstehungstag war aber nur zufällig ein Sonntag. Es ist also nötig, dass der Frühlings-Vollmond richtig vorausgesagt wird (Anmerkung 4). Zur erneuten Vereinfachung wird mit dem langfristigen Mittelwert der ziemlich variablen Mond-Umlauf-Zeit gerechnet. Bei der Reform wurde auf einen genaueren Mittelwert als den bisher verwendeten umgestellt. 7. Die Oster-Rechnung bis zur Kalender-Reform ↑ Anfang
Um die Vollmond-Tage im Sonnen-Kalender anzugeben, bezog man sich seit Anfang der Oster-Rechnung (Computus) im frühen
Mittelalter auf das bereits den Babyloniern bekannte Meton'sche Verhältnis, dass 19 Sonnen-Jahre (a) näherungsweise
gleich lang wie 235 Mond-Umläufe (Lunationen, Zeit pro Lunation =m) sind. Bis zur Kalender-Reform vernachlässigte man
den Fehler dieses Verhältnisses (bzw. man wusste es nicht besser), das als Gleichung wie folgt lautet: Ostern ist dann am ersten Sonntag nach dem Frühlings-Vollmond. Die Sonntage im Kalender anzugeben, ist der einfache letzte Schritt (Abb.6). Jeder für Ostern in Frage kommende Sonntag (im März oder April) ist im Folgejahr einen Tag früher im Kalender, in Schaltjahren zwei. Im Computus gibt es dafür den Sonntagsbuchstaben oder den Sonnenzirkel für das Kalenderjahr.
Hinweis: Abb.6 wurde für ein paar wenige aktuelle Jahre angefertigt. Das darin angewendete Verfahren ist sowohl vor der Reform als auch wenigstens zwischen zwei Säkular-Jahren (Hunderter) nach der Reform anwendbar. Ab 2014 wiederholen sich die Daten der Frühlingsvollmonde. Vorher erfolgt der sogenannte Mondsprung: nur +18 anstatt +19 Tage. 8. Die Oster-Rechnung seit der Kalender-Reform ↑ Anfang
Für die verbesserte Bestimmung des Osterdatums sind zwei voneinander unabhängige Korrekturen laufend nötig:
Den Frühlingsanfang nahe beim 21. März zu halten, dient primär dem Sonnenteil des Gregorianischen Kalenders. Die entsprechende Maßnahme ist eigenständig, heißt Sonnengleichung (Anmerkung 6) und ist schon im 1. Abschnitt beschrieben.
Die Mondgleichung
Der Mond-Fehler im Grundschema 19 aj = 235 m = 6.939,75 Tage In der als Mondgleichung bezeichneten Maßnahme wird das Mond-Datum im Durchschnitt alle 312,5 Tage einen Tag früher angesetzt.
Die periodische Korrektur der Oster-Rechnung
Da die beiden Korrekturen unterschiedliches Vorzeichen haben, heben sie sich manchmal gegenseitig auf (Anwendungen der Mondgleichung auch in Säkular-Jahren). Im Mittel wird der Frühlings-Vollmond aber stetig mit einer Rate von 1 Tag (d) in etwa 232½ Jahren (a) später im Kalender angegeben (Verminderung der Epakte e, in differentieller Schreibweise: de/dt = (3/400 - 8/2500) d/a = 1/232,56 d/a). 9. Die Oster-Rechnung in den alternativen Kalendern ↑ AnfangGegenüber dem Gregorianischen Kalender ändert sich nur die Sonnengleichung, denn die Mondgleichung hat keinen Bezug zu den Schaltungen, sie wäre getrennt zu variieren oder weiterhin wie im Gregorianischen Kalender anzuwenden. Im Gregorianischen Kalender ausfallende Schaltungen stören den olympischen 4-Jahres-Rhythmus nicht nachhaltig. Deshalb wäre bei den alternativen Kalendern auch mit einer Sonnenangleichung zu warten, bis die Summe der Schalt-Verschiebungen 4 Jahre beträgt, also gemäss julianischer Basis 1 Tag ausmacht.
Khayam-Kalender:
Matzka-Kalender:
Mädler-Kalender:
Zum Vergleich das Gregorianische Jahr: 10. Kritik an der Praxis der Oster-Rechnung ↑ AnfangDie Auswerte-Arbeit mit den Begriffen und Zahlen gemäss Computus ist uns fremd und erst nach einiger Zeit des Einübens möglich. Besonders nachteilig ist, dass man bei meist nicht zu umgehender schematischer Anwendung des Verfahrens keinen Einblick in die Grundlagen der Oster-Rechnung erhält und der Verdacht der Geheimniskrämerei entsteht. Es ist nicht verwunderlich, dass in der Neuzeit versucht wurde, das Problem mit Neuzeitlicher Mathematik einfacher darzustellen. Die bekannte Osterformel von Carl Friedrich Gauss ist aber in Wirklichkeit ein Satz mehrerer Formeln [9]. Es sind umso mehr, wenn man will, dass nicht zu viel von den Zusammenhängen in unpraktisch langen Formeln untergebracht ist. Als Vorteil ist zu werten, dass man keine aus Jahrbüchern o.ä. zu entnehmende Kennzahlen benötigt. Der Besitz der Formelsammlung genügt für alle Zeit. Gauss berücksichtigt sowohl die Sonnen- als auch die Mondgleichung. Die seltene, historisch begründete Ausnahme, dass ein ermittelter 26. April in den 19. April umzuwandeln und darauf zu achten ist, dass Ostern innerhalb 19 Jahren (Meton-Periode) nicht ein zweites mal auf den 25. April fällt, hat er aber nicht in seinen Formeln unterbringen können. Das ist erst einem Mathematiker unserer Zeit gelungen [11].
Auch die Anwendung der Gauss'schen Formel(n) ist ein schematischer Brauch ohne vertiefenden Einblick. Die zusammenfassende Feststellung lautet deshalb: 11. Literatur ↑ Anfang
[1] Arno Borst: "Computus Zeit und Zahl in der Geschichte Europas", Wagenbach 1990 12. Anmerkungen ↑ Anfang
Anmerkung 1
Anmerkung 2 Alle bisherigen Iranischen Kalender sind nicht wie der Julianische und der Gregorianische Kalender gänzlich vorausberechnet (zyklischer Kalender) [10]. Der Frühlingsbeginn, der gleichzeitig der Neujahrstag ist, wird jährlich festgestellt (astronomischer Kalender), sodass der 33-Jahre-Schalt-Zyklus in seltenen Fällen gestört wird. ↑ zurück
Anmerkung 4
Anmerkung 5
Anmerkung 6
Anmerkung 7
Anmerkung 8 + 310: (1900) 2210 2520 2830 3140 ab Jahr: (1900) 2028 2156 2284 2412 2540 2668 2796 2924 3052 3180 3308 3436 Epakte1: (O) 29 28 28 27 27 26 25 25 24 24 23 22 + 310: 3450 3760 4070 4380 4690 5000 ab Jahr: 3564 3692 3820 3948 4076 4204 4332 4460 4588 4716 4844 4972 5100 Epakte1: 22 21 21 20 20 19 18 18 17 17 16 15 15 Epakte1 = Epakte für Jahre mit Goldener Zahl 1 Epakte und Goldene Zahl kennzeichnen ein Kalenderjahr bezüglich ihres Frühlingsvollmond- Datums. Der Vorteil dieses Vorschlags ist, dass die Epakte immer nur fällt (das Frühlingsvollmond-Datum immer nur größer wird), niemals zwischendurch steigt, wie in der Gregorianischen Regelung. ↑ zurück 13. Nachtrag (2011): Der Milankovic-Zyklus ↑ AnfangDie Orthodoxen Kirchen beschlossen 1924, einen vom serbischen Physiker und Mathematiker Milutin Milankovic leicht verbesserten Gregorianischen Kalender einzuführen. Weil sich die Russisch-orthodoxe Kirche aufgrund der politischen Wirren nach der Oktoberrevolution am Beschluss nicht beteiligen konnte, verschoben einige orthodoxe Kirchen (z.B. das Patriarchat von Jerusalem und die Serbisch-orthodoxe Kirche) dessen Umsetzung. Dabei ist es bis heute geblieben. Der sogenannte Neu-Julianische, Neue, oder Orthodoxe Kalender wird nur im Patriarchat von Konstantinopel mitsamt der Griechisch-orthodoxen Kirche und der Bulgarisch-orthodoxen Kirche angewendet. Da das Gregorianische Kalenderjahr immer noch etwas zu lang ist, hat Milankovic die Schaltjahrregelung verändert. In 900 Jahren fallen gegenüber dem Julianischen Kalender 7 Schalttage weg (7/900 = 7,78·10-3). Im Gregorianischen Kalender ist der durchschnittliche Wegfall kleiner, nämlich 3 Tage in 400 Jahren (3/400 = 7,75·10-3).
Die Regel im Gregorianischen Kalender, dass alle durch 400 ohne Rest teilbaren Jahre (ihre Zahlen) Schaltjahre sind, wurde verändert zu:
Die in die Übersicht (5.) einzutragenden Werte sind: Die Jahrlänge ist im Milankovic-Zyklus besser als im Gregorianischen Zyklus. Trotz der größeren Zykluslänge ist auch der Mangelwert (Zemanek) besser (kleiner). Die Jahrlänge ist auch besser als im Khayam-Zyklus. Wegen der im Khayam-Zyklus sehr kleinen Zykluslänge ist dennoch dessen Mangelwert (Zemanek) kleiner als im Milankovic-Zyklus. Die Osterrechnung sollte im Neuen Kalender gleich wie im Gregorianischen Kalender erfolgen. Dieser Teil des Beschlusses wurde nirgends verwirklicht. Die Orthodoxe Kirche Finnlands ist die einzige orthodoxe Kirche, die so rechnet, wofür sie sich aber schon vor 1924 mit der kompletten Annahme des Gregorianischen Kalenders entschieden hatte. Die veränderte Schaltjahrregelung verändert die Sonnengleichung. Über eine etwaige Änderung der Mondgleichung ist nichts bekannt.
Siegfried Wetzel, CH 3400 Burgdorf, März 2008 (Apr.08, Aug.11, Jan.12)
↑↑ Anfang |
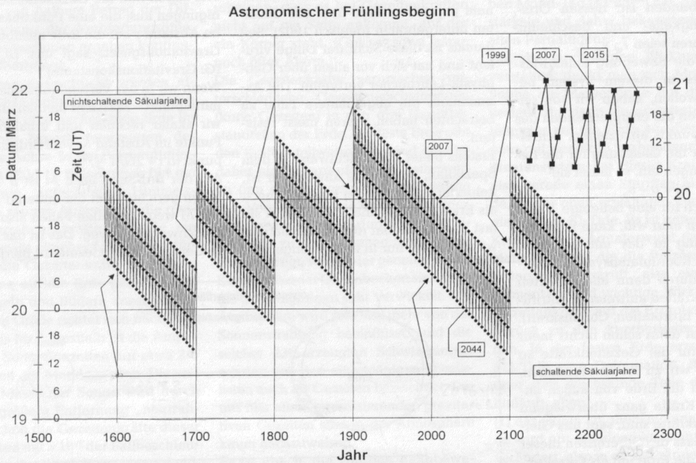Abb.1 Gregorianischer Kalender, astronomischer Frühlingsbeginn [4]
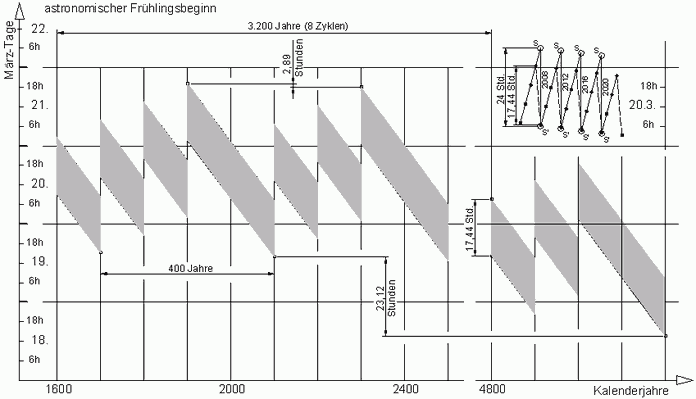Abb.2 Gregorianischer Kalender, astronomischer Frühlingsbeginn (Abb.1 vereinfacht und verlängert)
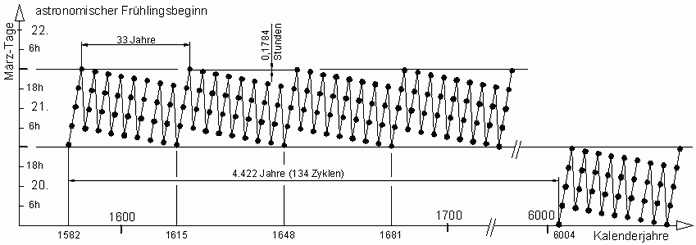Abb.3 Khayam-Kalender, astronomischer Frühlingsbeginn
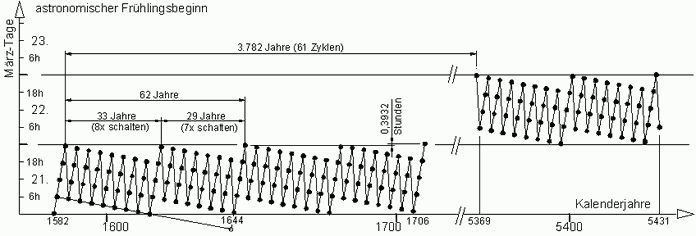Abb.4 Matzka-Kalender, astronomischer Frühlingsbeginn 
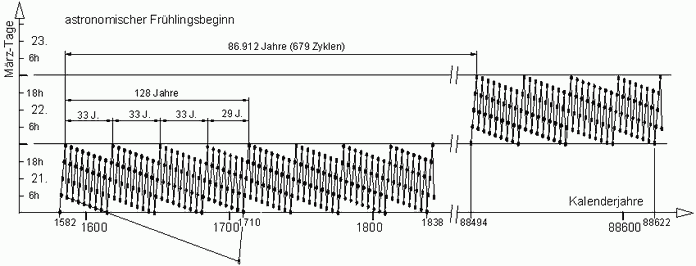Abb.5 Mädler-Kalender, astronomischer Frühlingsbeginn
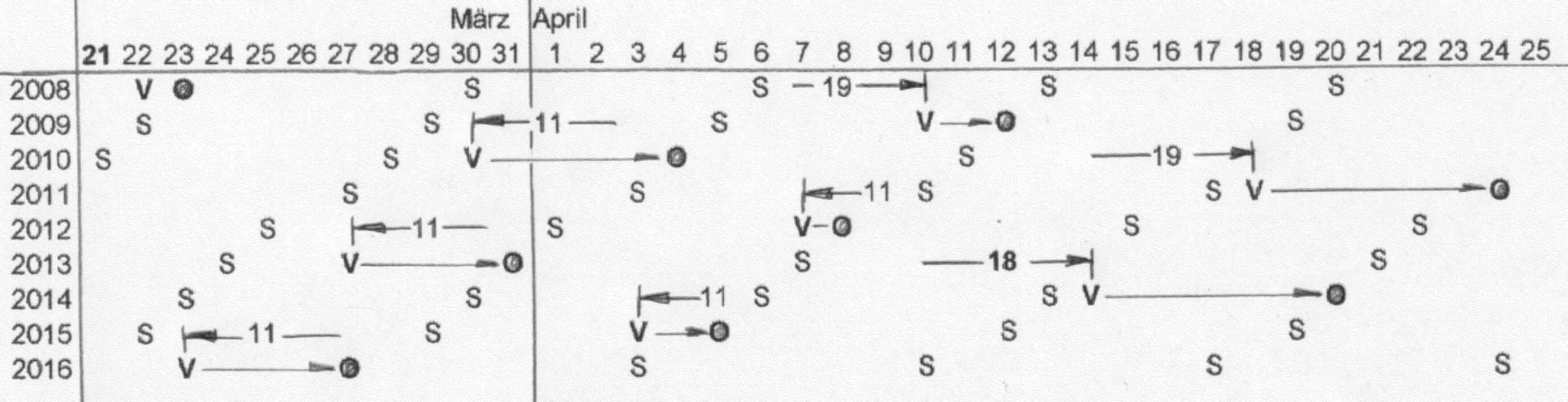Abb.6 Frühlings-Vollmonde (V), Sonntage (S) und Oster-Sonntage (O) für die Jahre 2008 bis 2016