LogoSW

<< Home
<< andere Sonnenuhren-Beiträge

 ↓↓ Ende

Analemmatische Sonnenuhr nach Foster und Lambert

Zusammenfassung

Abb.1 Analemmatische Sonnenuhr aus dem 16. Jahrhundert in Brou bei Bourg en Bresse / F
Der schattenwerfende Stab ist angekettet.

Die Skala einer analemmatischen Sonnenuhr ist im Allgemeinen elliptisch. Der in der Ellipse enthaltene Sonnderfall Kreis ist die Skalenform der analemmatischen Sonnenuhr nach Foster und Lambert. Die vorliegende Darstellung führt bis zu einer Foster/Lambert-Uhr mit polarem Zifferblatt (die Richtung zum Nordpol des Himmels ist im Zifferblatt enthalten). In ihr wird die Parallelität mit der Himmelsachse zur jahreszeitlichen Einstellung des Schattenstabes mit einer Hilfsvorrichtung ausgenutzt. Diese Möglichkeit gilt allgemein, die Skala muss nicht kreisförmig wie in der Foster/Lambert-Version sein. Man kann auch die polare Verschiebung der Hilfsvorrichtung auf ein nicht polar angeordnetes Zifferblatt übertragen.

Inhalt

1. Die interaktive analemmatische Sonnenuhr in der Öffentlichkeit
2. Das Grundprinzip
3. Das Grundprinzip der Foster/Lambert-Sonnenuhr
4. Doppelte Foster/Lambert-Sonnenuhr
5. Kombination einer polaren Foster/Lambert-Sonnenuhr mit einem Äquatorring
6. Eine vertikale analemmatische Sonnenuhr mit Deklinationskompensator
7. Anhang: Eine digitale äquatoriale Ringsonnenuhr
8. Literatur


1. Die interaktive analemmatische Sonnenuhr in der Öffentlichkeit  ↑ Anfang

Analemmatische Sonnenuhren mit elliptischer Stundenskala sind heute sehr beliebt. Häufig ist eine solche in einem öffentlichen Park anzutreffen mit der Besonderheit, dass der Benutzer als Schattenwerfer selbst Teil der Uhr wird. Dabei geht es allerdings nicht nur um die aktive Beteiligung des Benutzers. Da dieser den losen, weil entlang einer Skala auf der kleinen Ellipsenachse aufzustellenden stabförmigen Schattenwerfer ersetzt, muss ein solcher auch nicht angekettet werden, um sein Verschwinden zu erschweren.

2. Das Grundprinzip  ↑ Anfang

Kennzeichen ist die elliptische Form der Stundenskala. Da ein Kreis bei schräger Betrachtung oder Projektion als Ellipse erscheint, wäre nach einem solchen Kreis bei der Bewegung der Sonne zu suchen. Denn eine Sonnenuhr bildet die (scheinbare) Bewegung der Sonne am Himmel ab und deutet sie als Änderung der Zeit. Die Tagesbahn der Sonne ist tatsächlich ein Kreis. In einer äquatorialen Ringsonnenuhr wird das anschaulich: dort wird die Sonnenbahn wieder auf einer kreisförmigen Skala abgebildet. Wird die Tagesbahn der Sonne oder ihr Bild - der genannte handfeste Ring - auf den Boden projiziert, ist die fragliche Ellipse gefunden.

Art und Richtung der gedachten Projektion und Projektionsfläche sind an sich beliebig. Als Standard-Form der analemmatischen Sonnenuhr gilt die Parallelprojektion des gedachten Rings senkrecht auf den Boden (Horizontfläche). Der schattenwerfende Punkt ist in gleicher Richtung gegen den Boden zu verschieben. Im Unterschied zur äquatorialen Ringsonnenuhr sind es über den Tag viele verschiedene Punkte, deren Schatten auf die elliptische Bodenskala fällt. Deshalb ist ein Stab nötig, der die unterschiedlichen erforderlichen Punkte für die aufeinander folgenden Stunden enthält. Die Schattenrichtung des Stabes als Ganzes spielt keine Rolle, wichtig ist nur diejenige Stelle, die die elliptische Skala trifft (Abb.2, [1] und [2]). Die senkrechte Projektion ermöglicht einzig die senkrechte Aufstellung des Schattenstabs bzw. das aufrechte Stehen des Benutzers in seiner Rolle als Stabersatz.

Abb.2 Analemmatische Sonnenuhr, Standard-Form:
zur Anschaung am Schattenstab angebrachter kleiner verschiebbarer Querstab, dessen Schatten auf die elliptische Skala fällt; Querstab kennzeichnet den momentan wirksamen schattenwerfenden Punkt, [2]

Selbst die gedachte äquatoriale Ringsonnenuhr hat einen Schattenstab. In ihm sind alle über ein Jahr wirksamen schattenwerfenden Punkte zusammengefasst. Er ist parallel zur Erdachse angeordnet, funktioniert aber ebenso wenig wie der Stab der analemmatischen Uhr als Werfer eines Linienschattens. Der wirksame Punkt ändert sich von Tag zu Tag zwischen zwei Endlagen an den Solstitien (Sommer- und Wintersonnenwende). Der Stab der Bodenuhr muss ihm analog folgen: tägliches Verstellen auf der kleinen Ellipsenachse.

3. Das Grundprinzip der Foster/Lambert-Sonnenuhr   ↑ Anfang

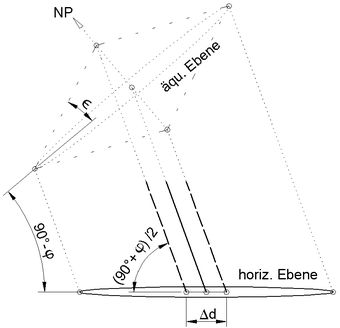← Abb.3 Grundprinzip der Foster/Lambert-Sonnenuhr:
Die gedachte äquatoriale Ringsonnenuhr wird in "mittlerer" Projektionsrichtung ((90° + φ) / 2) auf das horizontale Zifferblatt verschoben.

↓↓ Abb.4 Foster/Lambert-Sonnenuhr in Muttenz/CH/BL

Die Standard-Form wurde vermutlich zuerst vom Franzosen Vauzelard angegeben. Zur gleichen Zeit (17. Jahrhundert) wurde aber auch schon eine Sonder-Form beschrieben. Es handelt sich dabei um die vom Engländer Foster benutzte "mittlere" Projektionsrichtung, bei der das Bild eines Kreises wieder ein Kreis ist. Sie schneidet die Äquatorebene mit dem gedachten Sonnenuhrenring und die Projektionsfläche im gleichen Winkel ((90°+φ)/2, Abb.3). Der Skalenring der analemmatischen Sonnenuhr ist kreisförmig und gleichmässig unterteilt. Man kann ihn beim Umstellen zwischen Normal- und Sommerzeit hin- und herdrehen. Die Interaktion mit dem Benutzer besteht aber nicht mehr, denn der Schattenstab ist z.B. gegen den Boden geneigt. Der Vorschlag von Foster blieb zunächst unbeachtet. Seit der Neuentdeckung im 18. Jahrhundert durch den Elsässer Lambert wird die entsprechende Uhr als Foster/Lambert-Sonnenuhr bezeichnet.

4. Doppelte Foster/Lambert-Sonnenuhr   ↑ Anfang

Da zwischen zwei Ebenen zwei verschiedene Schnittwinkel existieren (einer <90° und einer >90°), gibt es auch eine zweite Projektionsrichtung für eine Foster/Lambert-Uhr. Diese Projektionsrichtung schneidet die beiden Ebenen mit je (90°-φ)/2, also flacher (Abb.4, Mitte) als die erste. Wegen des folglich stark geneigten und bis über die Skala hinaus zu verschiebenden Schattenstabs ist diese Lösung allerdings nicht besonders praktisch.

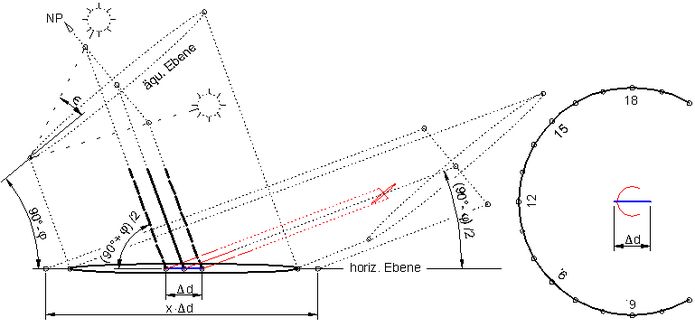Abb.5 Foster/Lambert-Sonnenuhr mit nach Norden ("Norduhr") oder nach Süden ("Süduhr") geneigtem Schattenstab
schwarz: von gleich groß gedachter äquatorialer Ringsonnenuhr ausgehend
rot: verkleinerte "Süduhr" für gleich große Jahresverschiebung beider Stäbe

Sollen die beiden Schattenstäbe jahreszeitlich gemeinsam verstellt werden, so besteht bereits in mittleren geografischen Breiten ein großes "Missverhältnis" (Verhälnis x in Abb.5, links) zwischen den beiden Kreisskalen-Größen (schwarze und rote Skala in Abb.5, rechts). Beide Skalen werden gleich groß, wenn man eine solche Doppeluhr für den Äquator anfertigt. Rohr beschrieb diese Übung, aus der die sogenannte "rektilineare Uhr" hervorging (Abb.6, [3]). Dabei handelt es sich um die symmetrische Doppeluhr, die am Äquator Boden-Uhr ist und in mittleren geografischen Breiten in polarer Lage aufgestellt wird.

Abb.6 Doppelte Foster/Lambert-Sonnenuhr ("rektilineare Uhr", zum Himmesnordpol nach oben rechts, [3])

5. Kombination einer polaren Foster/Lambert-Sonnenuhr mit einem Äquatorbogen   ↑ Anfang

Eine in mittlerer geographischer nördlicher Breite aufgestellte Foster/Lambert-Sonnenuhr wurde kürzlich in Kombination mit einem zusätzlichen äquatorparallelen Ring unter der Bezeichnung Analemmatische Sonnenuhr mit Deklinationskompensator bekannt. (Abb.7, [4]). Dabei handelt es sich um den Nordteil ("Norduhr") der o.g. "rektilinearen Uhr", wobei die Projektion auf eine nach Westen verdrehte polare Fläche erfolgte (Anzeige zur Sommersonnenwende bis Sonnenuntergang).

Das eigentlich Besondere an dieser Sonnenuhr ist, dass mit dem zusätzlichen äquatorparallelen Halbring (Äquatorbogen) die Deklination der Sonne gemessen und für die Einstellung des schattenwerfenden Stabs verwendet wird. Halbring und Stab befinden sich gemeinsam auf dem in polarer Richtung zu bewegenden Schieber, der so eingestellt wird, dass der Schatten des Rings auf eine Zifferblatt-feste Marke der Ringachse fällt. Der Abstand des Schattens von der Ringebene (Äquatorebene) ist gleich groß wie der von der Sonnendeklination abhängige Abstand des Nodus vom Ring und - was entscheidend ist- gleich groß wie der Abstand des Schattenwerferfußpunktes der Sonnenuhr vom Mittelpunkt des Skalenkreises.

Abb.7 Polare Foster/Lambert-Sonnenuhr mit einem als "Deklinationskompensator" verwendeten äquatorialen Halbring, zum Himmesnordpol nach oben links, [4]
Äquatorbogen und Schattenstab zusammenhängend
Zifferblatt u. Deklinations-Marke zusammenhängend

Details zur vorgestellten Sonnenuhr

Beim Verstellen zur Deklinations-Anpassung wird der Stiel des Äquatorring-Halters (Form einer zum Zeichen benutzten T-förmigen Reißschiene) gegen den Zifferblatt-Halbkreis (Form eines zum Zeichen benutzten Winkelmessers) verschoben.
Die kleine scheibenförmige Einstellmarke ist fest mit dem Zifferblatt verbunden.

Offensichtlich wurde die Neigung (Inklination) des Zifferblatts als runder Betrag 60° vorgegeben, woraus sich die "beliebig anmutende" Skalierung ergab: kein Bezug zur Symmetrieachse des Zifferblatt-Halbkreises, Zifferblatt auf der Nachmittagsseite nicht ausgenutzt (bei φ = 48¼° am Aufstellort Sonnenuntergang zur Sommersonnenwende früher als 8 Uhr).

Die Korrektur dafür, dass die Stundenpunkte der Skala mit der Symmetrieachse des Zifferblatt-Halbkreises korrespondieren, wäre:

  1. z.B. 3 Uhr WOZ auf der Symmetrieachse: 45°-Drehung des Zifferblattes um die Polachse >> Inklination 61,9°
    )**,

  2. z.B. 4 Uhr MESZ )* auf der Symmetrieachse: 43,84°-Drehung (Aufstellort liegt 1,16° westlich de 15. östlichen Längengrads) des Zifferblattes um die Polachse >> Inklination 61,3° )**.
    )* Die Anzeige ist mit den Werten der Zeitgleichung fehlerhaft.
)** Die angegebenen Werte können z.B. durch Koordinatentransformation zwischen ruhenden Äquator- und
     Horizont-Koordinaten ermittelt werden.

Um die Skala auszunutzen, wäre das Zifferblatt 15° weniger um die Polachse zu drehen

6. Eine vertikale analemmatische Sonnenuhr mit Deklinationskompensator   ↑ Anfang

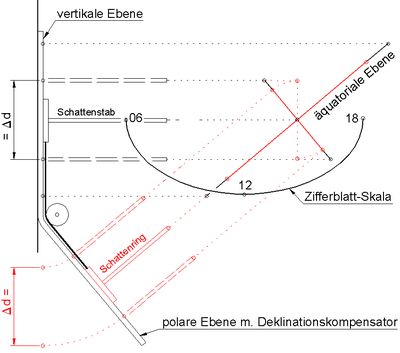Abb.8 Vertikale analemmatische Sonnenuhr mit Deklinationskompensator, Entwurf, schematisch

Die Anwendung des oben beschriebenen Deklinationskompensators in einer analemmatischen Sonnenuhr ist weder auf deren Form als Foster/Lambert-Uhr noch auf die polare Zifferblatt-Lage beschränkt. Da der zusätliche materielle Aufwand in Form des Äquatorbogens und der Gewinn, die Deklination nicht kennen zu müssen, sich die Waage halten, soll wenigstens gezeigt werden, dass der hinzuzufügende Äquatorbogen bei anderer als polarer Zifferblattlage kleiner ausfällt.

In jeder anderen als in einer polaren Fläche ist das projizierte Bild des Schattenstabs der gedachten äquatorialen Ringsonnenuhr kleiner als der Stab. Man kann folglich die kleinere polare Einstellbewegung eines kleineren Äquatorbogens nutzen, muss diese aber in die nicht-polare Zifferblattebene übertragen (Abb.8). Letzteres eliminiert allerdings den verkleinerten Aufwand wieder etwas.


7. Anhang: Eine digitale äquatoriale Ringsonnenuhr   ↑ Anfang

Der Äquatorbogen des Deklinationskompensators erinnerte mich an eine alte Idee für eine digitale äquatoriale Ringsonnenuhr (Abb. 9 u. 10). Deren obere Hälfte wird wie der Deklinationskompensator jahreszeitlich in polarer Richtung verschoben. Sie und die feste untere Hälfte wirken zusammen als äquatoriale Sonnenuhr. Die Funktion ist digital. Es gibt nicht den einen schattenwerfenden Stab (Polstab; die Ringmitte ist leer) sondern eine Reihe von Löchern - genauer: lichtdurchlassenden Röhren - im oberen Halbring (z.B. 12 Stück) und Skalenpunkte auf der Innenseite des unteren Halbrings (z.B. 12 Stundenpunkte). Die Sonne scheint immer nur durch ein oder zwei benachbarte Röhren. Der "Schwerpunkt" der maximal zwei Lichtflecke zeigt auf dem skalierten unteren Halbring die Zeit an. Die schrittweise Anzeige durch sich folgende Punkte kann als digitale Messmethode bezeichnet werden.

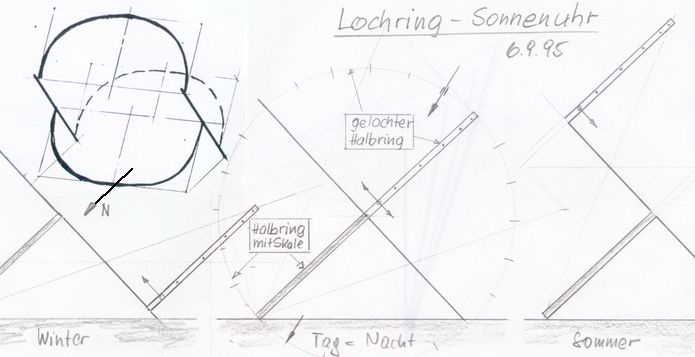Abb.9 Idee einer digitalen äquatorialen Ringsonnenuhr

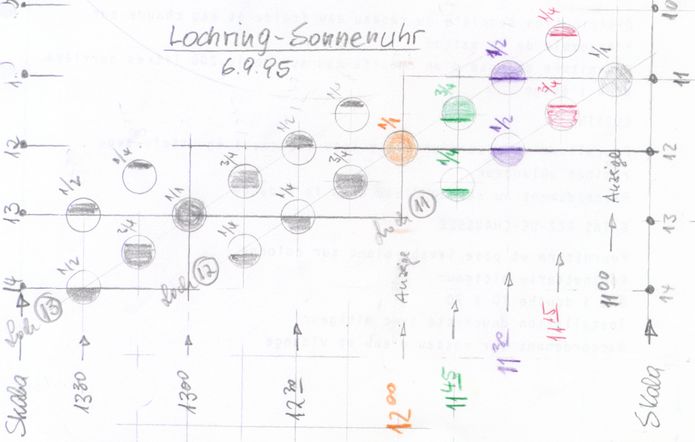Die lichtdurchlassenden Röhren sind an einem Ende kreisförmig, am anderen Ende mit einem langen Oval begrenzt. In den Stundenebenen bilden die beiden Begrenzungen einen Trichter mit einem Öffnungswinkel von 2 mal ε = 23,44°. Meine schon vorgenommene Konstruktion mit mehr as Halbringen ermöglicht sowohl die Anzeige von Sonnenauf- und -untergang an den Tag/Nacht-Gleichen (6 Uhr und 18 Uhr) als auch der frühen und späten Stunden im Sommerhalbjahr. Ihr Bau lässt aber immer noch (Jan.12) auf sich warten.

Abb.10 Digitale äquatoriale Ringsonnenuhr, vom Norden aus beschriftetes Anzeigeschema

8. Literatur   ↑ Anfang

[1] S. Wetzel: Modell für die Ableitung der analemmatischen Sonnenuhr aus einer äquatorialen Ring-Sonnenuhr
[2] S. Wetzel: Eine mathematische Beschreibung der Analemmatische Sonnenuhr
[3] René R. J. Rohr: "Die Sonnenuhr", Callwey, 1982, Seiten 124 bis 128
[4] Walter Hoffmann: "Eine analemmatische Sonnenuhr von Hans Kolar" , Arbeitsgruppe Sonnenuhren im
    Österreichischen Astronomischen Verein, Rundschreiben Nr. 42

LogoSW Siegfried Wetzel, CH 3400 Burgdorf, Januar 2012 (Juni 13, Sept. 15)

 ↑↑ Anfang

<< Home
<< andere Sonnenuhren-Beiträge