<< Home
<< andere Sonnenuhren-Beiträge
↓↓ Ende
Modell für die Ableitung der analemmatischen Sonnenuhr
aus einer äquatorialen Ring-Sonnenuhr
(DGC-Jahresschrift 2004)
Zusammenfassung
Für die Erklärung der Analemmatischen Sonnenuhr mit Hilfe einer Äquatorialen Ring-Sonnenuhr wird ein durch Verschieben veränderliches Modell verwendet. Durch die Verschiebung des Schatten-werfenden Punktes in den und im Schattenstab wird auch dessen Funktion anschaulich gemacht, was bisherige Autoren unterlassen.
Inhalt
1. Einleitung
2. Verwendung einer Ring-förmigen Äquatorialen Sonnenuhr
3. Schatten-Stäbe als gerade Reihen unendlich vieler Schatten-werfender Punkte
4. Der Begriff Projektion und der Vorgang Verschiebung
5. Literatur
6. Anhang: Gleichungen der Schattenstab-Skala und der Verschiebung
1. Einleitung ↑ Anfang
Es soll die Standard-Version der Analemmatischen Sonnenuhr, die vermutlich erstmals 1640/1644 von Vaulezard [1] beschrieben wurde, aus einer Äquatorialen Ring-Sonnenuhr, von der 1951/ 1953 auch Terpstra in seinen oft zitierten Überlegungen ausging, abgeleitet werden. Das älteste noch existierende Exemplar einer solchen Sonnenuhr befindet sich vor der Kathedrale in Brou bei Bourg-en-Bresse in Frankreich. Bild 1 ist eine Fotografie dieser Uhr aus dem Jahre 1996, leider ohne Sonnenschein. Der Mittags-Schatten würde nach links oben fallen. Der verstellbare Schattenstab ist gegen Entwendung mit einer Kette gesichert.

<< Bild 1 Analemmatische Sonnenuhr in Brou bei Bourg-en-Bresse in Frankreich
Terpstra stellt geometrische Überlegungen an und führt die Ableitung mit Projektion durch. Für den Schatten-Stab der Analemmatischen Sonnenuhr findet er so aber nur den veränderlichen Fuss-Punkt. Die Funktion dieses Stabes erklärt er, ohne auf die Äquatoriale Sonnenuhr zurück zu greifen [2]. Mit Hilfe eines veränderbaren Modells lässt sich die Analemmatische Sonnenuhr durch physische Verschiebung aus der Äquatorialen Sonnenuhr herleiten. Deren Schatten-werfender Punkt findet sich nach der Verschiebung im Schatten-Stab der Analemmatischen Sonnenuhr wieder.
Zur Beschreibung dienen ausschliesslich Fotografien des Modells in seinen verschiedenen Zuständen auf dem Wege von der einen zur anderen Sonnenuhr.
2. Verwendung einer Ring-förmigen Äquatorialen Sonnenuhr ↑ Anfang
Bild 2 zeigt beide Sonnenuhren übereinander angeordnet. Der senkrechte Stab ist der auf der Analemmatischen Sonnenuhr einzustellende Schatten-Werfer. Der geneigte Stab ist zwar auch auf dieser Sonnenuhr befestigt, gehört aber zur Äquatorialen Sonnenuhr und ist ein Polstab. Deren Zifferblatt hat in der Mitte eine kreisförmige Öffnung, an deren Rand der Ziffern-Kreis gezeichnet ist, der allein wichtige Teil in der Anzeige-Ebene der verwendeten Äquatorialen Sonnenuhr. Das ist eine Ring-förmige und nicht die ebene Standard-Version der Äquatorialen Sonnenuhr.
Der Ring bzw. Kreis ist einerseits nötig, damit bei senkrechter Parallelprojektion auf die horizontale Ebene eine Ellipse entsteht (erste der beiden von Terpstra formulierten Konstruktions-Vorschriften, s. Bild 2). Andererseits ist in der Analemmatischen Sonnenuhr ein Punkt-Schatten wirksam, genau wie bei der Äquatorialen Ring-Sonnenuhr. Es zählt nur der Kreuzungs-Punkt zwischen Stab-Schatten und Ellipse bzw. Kreis.
3. Schatten-Stäbe als gerade Reihen unendlich vieler Schatten-werfender Punkte ↑ Anfang
Dass in beiden Sonnenuhren je ein Schatten-werfender Stab vorkommt, vewundert also zunächst. Nötig ist doch nur der Schatten von einem in der Regel nicht fixem Punkt. Weil aber jeder der beiden Stäbe den in jedem Moment nötigen Punkt enthält (jeder Stab ist die gerade Reihe von unendlich vielen Punkten), können Stäbe verwendet werden. Bei der Äquatorialen Sonnenuhr sind wir letztlich froh über dieses uns zufallende Geschenk.
Für das Verständnis müssen die Stäbe in Punkte aufgelöst werden. Wir beginnen beim Polstab der Äquatorialen Sonnenuhr. Von den unendlich vielen - die Sonnen-Deklination ändert sich täglich - sind 7 Punkte als kleine Kugeln dargestellt. Von jedem geht der den Skalen-Kreis treffende Schatten annähernd während eines ganzen Tages aus. Diese Punkte teilen das Jahr in die durch die 12 Tierkreiszeichen gekennzeichneten Abschnitte. Die senkrechte Parallelprojektion der Polstab-Skala ist die Datums-Skala der Analemmatischen Sonnenuhr (zweite der von Terpstra angegeben Konstruktions-Vorschriften, s. Bild 3), auf der der senkrechte Schatten-Stab täglich neu zu positionieren ist.
 Bild 2: Ring-förmige Äquator- und Analemmatische Sonnenuhr
Bild 2: Ring-förmige Äquator- und Analemmatische Sonnenuhr
Bild 3: Äquatoriale Sonnenuhr: Polstab mit Datums-Skala
In den Bildern 4 und 5 ist die Schatten-werfende Funktion der beiden Endpunkte der Polstab-Skala gezeigt. Der obere Punkt wirkt bei Sommersonnenwende, der untere bei Wintersonnenwende. Von ihren unendlich vielen Schatten-Strahlen, die pro Tag einen Kegelmantel bilden, ist für jede zweite volle Stunde einer als Linie auf durchscheinender Folie gezeichnet. Weil das Modell für die geographische Breite φ=49° ausgelegt ist, reicht das Linienbüschel gerade von Sonnen-Aufgang bis Sonnen-Untergang (Endlinien sind horizontal).
 Bild 4: Äquatoriale Sonnenuhr: zwei Schatten-Kegel (Sonnenwend-Tage)
Bild 4: Äquatoriale Sonnenuhr: zwei Schatten-Kegel (Sonnenwend-Tage)
Bild 5: Äquatoriale Sonnenuhr: Schatten-Strahlen an Sonnenwend-Tagen
4. Der Begriff Projektion und der Vorgang Verschiebung ↑ Anfang
Die beiden erwähnten und bekannten Konstruktions-Vorschriften, mit denen eine Analemmatische Sonnenuhr erstellt werden kann, und die sich auf die Verwandtschaft der Analemmatischen Sonnenuhr mit einer Äquatorialen Sonnenuhr beziehen, erfüllen den von Terpstra als "einfachen Beweis" der Analemmatischen Sonnenuhr formulierten Anspruch nicht ausreichend [3]. Mit dem mathematischen (oder auch optischen) Begriff Projektion ist dem Schritt vom Polstab (oder wie bereits präzisiert: Polstab-Skala) zum senkrechten Schattenstab (oder zur Schattenstab-Skala, siehe später) nicht beizukommen. Er führt nur zu seinem Fuss-Punkt. Für die Behandlung des Stabes als Ganzes erweist sich der Vorgang der Verschiebung als geeigneter [4].
 Bild 6: Äquatoriale Sonnenuhr mit Acrylglas-Scheiben zur Sommer-Sonnenwende
Bild 6: Äquatoriale Sonnenuhr mit Acrylglas-Scheiben zur Sommer-Sonnenwende
Bild 7: Acrylglas-Scheiben zur Sommer-Sonnenwende, eine ÄquatorialeSonnenuhr darstellend
In den Bildern 6 und 7 ist die Situation bei Sommersonnenwende nochmals aufgenommen. Die sich im Intervall von zwei Stunden folgenden Tripel ( Schatten-Werfer + Schatten-Strahl + Punkt-Schatten) werden jetzt durch die oberen Kanten von senkrecht auf dem Zifferblatt der Analemmatischen Sonnenuhr stehenden Acrylglas-Scheiben simuliert. Das innere Kanten-Ende ist der Schatten-Werfer, das äussere der Punkt-Schatten, die Kante selbst ist der Schatten-Strahl.
In Bild 7 ist der Äquatoriale Ziffern-Kreis entfernt. Die horizontale Analemmatische Ziffern-Ellipse ist zu sehen. Nun werden die Scheiben parallel und senkrecht nach unten verschoben (sie sind in Schlitzen versenkbar), bis die aüsseren Kanten-Enden (die Punkt-Schatten) das horizontale Zifferblatt treffen und die Zeit dort anzeigen: Bild 8. Die inneren Kanten-Enden (die Schatten-werfenden Punkte) bilden nun nicht mehr einen gemeinsamen Punkt, sondern sie befinden sich alle in verschiedener Höhe (Ausnahme Vor/Nachmittags-Symmetrie) auf einer Geraden senkrecht unter dem Ausgangspunkt: Bilder 8 und 9. Das Tageszeit-abhängige Absenk-Mass ist in Bild 7 als überstehende Länge der äusseren Plattenkanten erkennbar. Am Mittag ist es minimal, bei Sonnen-Aufgang und Sonnen-Untergang (nach Absenken ist die Oberkante Zifferblatt-bündig) maximal.
Nur ein Stück des Tripels, nämlich der Schatten-Punkt endet sowohl durch Projektion als auch durch Verschiebung in der Projektions-Fläche (hier im Analemmatischen Zifferblatt). Die beiden anderen Stücke - Schatten-werfender Punkt und sein Schatten-Strahl - verbleiben nach der Verschiebung im Raum. Die Ausnahme gilt bei Sonnenauf- und -untergang, wenn alle Teile des Tripels in der horizontalen Ebene ankommen. Dieser Schatten-werfende Punkt ist dann zu einem Punkt der Datums-Skala - gleich wie bei Projektion - geworden.
 Bild 8: Acrylglas-Scheiben zur Sommer-Sonnenwende, eine Analemmatische Sonnenuhr darstellend
Bild 8: Acrylglas-Scheiben zur Sommer-Sonnenwende, eine Analemmatische Sonnenuhr darstellend
Bild 9: Acrylglas-Scheiben zur Sommer-Sonnenwende, eine Analemmatische Sonnenuhr darstellend,
Schatten-werfende Punkte markiert
In Bild 9 sind die alle zwei Stunden wirksamen Schatten-werfenden Punkte markiert. Ihre Verbindung zu einem Stab ist der ihre Stelle in Bild 2 einnehmende Schatten-Stab. Die Auflösung des Schattenstabs in Punkte ist die oben angekündigte Schattenstab-Skala. Über den Tag sind es unendlich viele Punkte. Sein Schatten besteht dann auch aus unendlich vielen Punkten. Der gültige ist der Kreuzungs-Punkt mit der Ziffern-Ellipse. Die Schattenstab-Skala ist somit für die Benutzung der Analemmatische Sonnenuhr nicht nötig, ist aber für ihr Verständnis sehr nützlich. Die Datums-Skala auf der Analemmatische Sonnenuhr ist hingegen täglich zu beachten, leider.
Nachdem der Schatten-werfenden Punkt jeweils so im Raum verschoben wurde, dass sein Schatten auf die entsprechende Stelle der in die Ellipse verschobenen Ziffer fällt, ist die Aufgabe erfüllt. Schatten-Strahlen werden nur im Modell verschoben. Zueinander parallele Paare gibt es in beiden Sonnenuhren, so wie es in beiden Uhren paralleles Sonnen-Licht gibt.
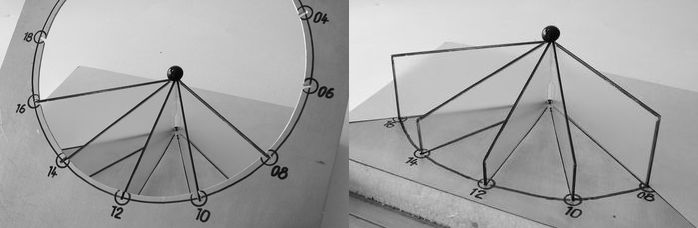 Bild 10: Äquatoriale Sonnenuhr mit Acrylglas-Scheiben zur Winter-Sonnenwende
Bild 10: Äquatoriale Sonnenuhr mit Acrylglas-Scheiben zur Winter-Sonnenwende
Bild 11: Acrylglas-Scheiben zur Winter-Sonnenwende, eine Äquatoriale Sonnenuhr darstellend
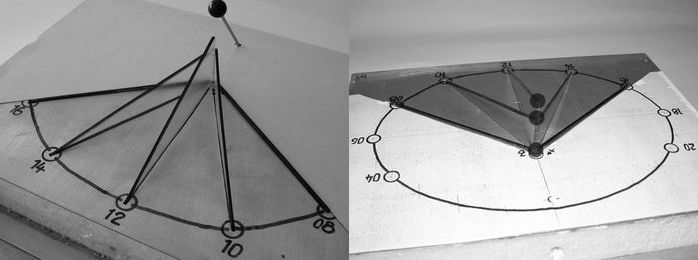 Bild 12: Acrylglas-Scheiben zur Winter-Sonnenwende, eine Analemmatische Sonnenuhr darstellend
Bild 12: Acrylglas-Scheiben zur Winter-Sonnenwende, eine Analemmatische Sonnenuhr darstellend
Bild 13: Acrylglas-Scheiben zur Winter-Sonnenwende, eine Analemmatische Sonnenuhr darstellend,
Schatten-werfende Punkte markiert
In den Bildern 10 bis 13 ist der bei Wintersonnenwende wiederholte Verschiebe-Vorgang gezeigt. Er ist analog zu dem bei Sommersonnenwende (Bilder 6 bis 9). Zwischen beiden Sonnenwenden liegen jeweils ca.182 Tage, an denen jedes Mal wieder eine andere Schattenstab-Skala gilt. Diese Skala wird im folgenden Abschnitt hergeleitet, der als fakultativer Anhang deklariert ist, damit das Vorhaben, sich nur auf Fotografien zu stützen, nicht unterlaufen wird.
5. Literatur ↑ Anfang
[1] M. de Vaulezard "Traité de l'origine, démonstration, construction et l'usage de cadran analemmatique" Paris, 1644
[2] P.Terpstra: "Zonnewijzers", Groningen, 1953
[3] P.Terpstra: "Een eenvoudig bewijs voor de gnomonzonnewijzer van Brou", Groningen, 1951
[4] S.Wetzel: "Sonnenuhren mit zusätzlicher Weltkarte auf dem Zifferblatt", Schriften der Freunde alter Uhren, 1998
6. Anhang: Gleichungen der Schattenstab-Skala und der Verschiebung ↑ Anfang
Die Schattenstab-Skala ist die Höhe h des Schatten-werfenden Punktes P über dem Stab-Fusspunkt F auf dem Analemmatischen Zifferblatt (s.Zeichnung 2). Diese Höhe ist gleich gross wie die vertikale Distanz des Schatten-werfenden Punktes von der Stundenziffer Z in beiden Sonnenuhren. Im Modell ist es die Steigung der oberen Kanten der Scheiben. Geräte-Konstante ist der Radius R des Äquatorialen Ziffern-Kreises (gleicher Wert wie grosse Halbachse der Analemmatischen Ziffern-Ellipse). Die astronomischen Variablen sind der Deklinationswinkel δ und der Stundenwinkel τ der Sonne. Ortsvariable ist die geografische Breite φ.
Schattenstab-Skala:
h = R (cosτ cosφ + tanδ sinφ) (s.Zeichnung 1).
Man beachte, dass diese Skala im Vergleich mit der Daten-Skala d auch eine Funktion der Tageszeit (Stundenwinkel τ) ist. Letztere lautet:
d = R tanδ cosφ [2].
Die Höhe ist maximal (Stab-Mindesthöhe) bei
δmax = +23,44° (Sommersonnenwende) und
τ = 0° (Mittag) und beträgt
hmax = R (cosφ + 0,434·sinφ).
Am Ort φ = 49° muss der Stab mindestens 0,9834·R lang sein.
Bei Sonnenauf- und -untergang geht der Schatten vom Fuss-Punkt F des Stabes aus:
h = 0 = R (cosτ cosφ + tanδ sinφ),
womit sich die Sonnenauf- bzw. -untergagszeit angeben lässt:
cos τSA/SU = -tanδ sinφ/cosφ = -tanδ tanφ.
Bei Sommersonnenwende am Ort φ = 49° ist τSA/SU = ± 120°.
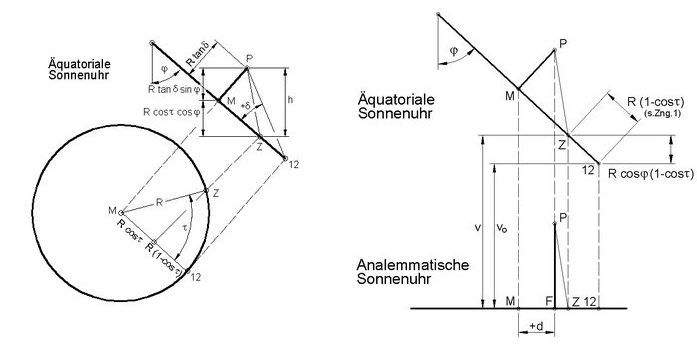 Zeichnung 1: Höhe des Schatten-werfenden Punktes über dem Zifferblatt, hier bei der Äquatorialen Sonnenuhr
Zeichnung 1: Höhe des Schatten-werfenden Punktes über dem Zifferblatt, hier bei der Äquatorialen Sonnenuhr
Zeichnung 2: Verschiebung im Modell von der Äquatorialen zur Analemmatischen Sonnenuhr
Als Zugabe sei noch die Verschiebung v aus der äquatorialen in die analemmatische Lage angegeben. Sie ist die Summe der Modell-Konstanten v0 und der Höhe der äquatorialen Stundenziffer Z über der 12 (siehe Zeichnmung 2). Im Modell sind es die überstehenden Längen der vertikalen Aussenkanten der Scheiben.
Verschiebung:
v = v0 + R cosφ (1-cosτ) (s.Zeichnung 2).
Die maximale Verschiebung ist für Sonnenauf- und -untergang bei Sommersonnen-wende vorzunehmen:
vmax = v0 + R cosφ (1-cos120°).
Am Ort φ = 49° beträgt dieser Maximalwert:
vmax = v0 + 1,5 R cos49° = v0 + 0,984 R.
![]() Siegfried Wetzel, CH 3400 Burgdorf, Januar 2008
Siegfried Wetzel, CH 3400 Burgdorf, Januar 2008
↑↑ Anfang
<< andere Sonnenuhren-Beiträge
Druck-Version (2-spaltig, 6 Seiten, *.pdf, 810 kB) >>
<< Home