<< Home
<< anderes Geometrisches
 ↓↓ Ende

Kreis- und Kugel-Förmiges

Zusammenfassung

Bei einem Besuch im Vasarely-Museum im Provencealischen Gordes Anfang der 90er Jahre (das Museum wurde erst 1997 geschlossen) begeisterten mich unter anderem die räumlichen Eindrücke, die Vasarely mit aneinander gereihten Kreisen erzeugte. Gleichzeitig waren für mich die Trichter-förmigen Einbrüche im Karstboden dieser Gegend neu. Ich versuchte, diese in scheinbar unendliche Tiefe führenden - dort Aven genannten - Trichter in der Op-Art Vasarely 's zu zeichnen. Aufbewahrt habe ich aber nur einen Entwurf für ein Uhren-Zifferblatt, auf dem umgekehrt am Rand ein Fall nach unten vorgetäuscht ist. Ich wechselte zu Kugeln, mit dem ich ein Aven im Dreidimensionalen nachbildete.

Angehängt sind ein paar Übungsstücke, die ich mir zum Begreifen (im wörtlichen Sinn) bekannter Kugel-Phänomene anfertigte.

Inhalt

1. Ein Uhren-Zifferblatt  ↑ Anfang

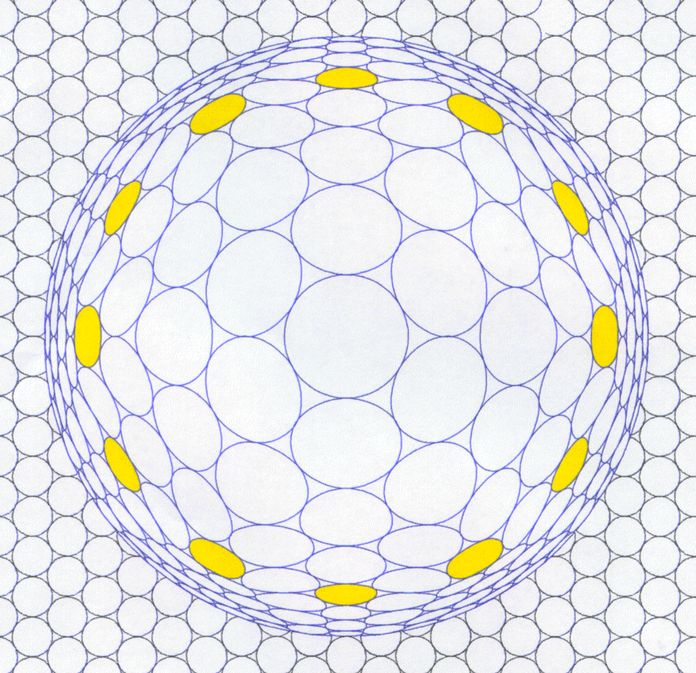
Für das Zifferblatt einer 1991 entstandenen SWATCH®-Armband-Uhr (Abb.1) wurde das Bild Vega-Tek von Vasarely verwendet. Es enthält ein Kreis-Arrangement, dass nicht zur 12er-Teilung einer Uhr passt. Die Stunden-Punkte wurden folglich bezuglos der verzerrten rechtwinkligen Aneinanderfügung von Kreisen übergestülpt. Mein Entwurf versucht, diesen Makel zu beheben.

Es war naheliegend - unter Beibehaltung eines Kreis-Arrangements - von der dichtest mögliche ebenen Kreis-Packung, bei der jeder Kreis lückenlos von sechs anderen Kreisen umgeben ist (wie die lückenlose Aneinanderreihung von Sechsecken, z.B. bei Bienenwaben), auszugehen. Ihre Rotations-Symetrie ist 60° (gleiches Bild nach 60° Drehung um den Mittelpunkt eines der Kreise). Es liegt eine 6er-Teilung des Umfangs vor, deren Halbierung (1/6 halbiert ist 1/12) zur für die Uhr nötigen 12er-Teilung führt. Die von SWATCH® angewendete 4er-Teilung würde bei der ersten Halbierung die 8er-Teilung und bei der zweiten Halbierung schon die ebenfalls nicht passende 16er-Teilung ergeben.

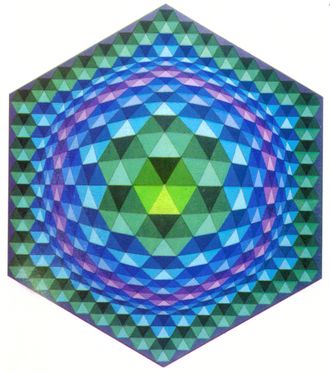Abb.1 Vasarely 's Bild Vega-Tek auf einer Armbanduhr        Abb.2 Vasarely 's Bild Tetcie-II

Vasarely hatte in seiner Vega-Serie im Bild Tetcie-II (Abb.2) die 6er-Teilung schon angewendet. Ich habe die darin enthaltenen (nochmals in Dreiecke unterteilten) Sechsecke durch Kreise ersetzt und die radiale Verzerrung in den 6 Hauptrichtungen und den dazwischen liegenden Richtungen verschieden gemacht. Es entstanden 12 ovale Marken (annähernd oval verzerrte Kreise etwa gleichen Flächeninhalts, farbig gefüllt) mit konstantem Abstand von der Mitte. Die Teilung auf diesem Marken-Kreis ist 24. Die Zwischen-Ovale sind gekippt, was nicht stört, da sie nur "Leere" darzustellen haben. Bei Vasarely liegen die entsprechenden Sechsecke auf einem 6er-Unrund, was für eine 12er Zifferblatt unpüassend ist. Abb.2a zeigt eine Küchenuhr, auf der ich meinen Entwurf anbrachte.

Abb.2a Küchenuhr: Zifferblatt mit verzerrtem (aufgeblähtem) Kreis-Raster

2. Ein Kugel-Trichter  ↑ Anfang

< Abb.3 Kugel-Trichter, vergrößertes Zentrum

Entfernteres erscheint kleiner, Näheres größer. Die dem zugrunde liegende Abbildung in Zentralperspektive findet außer beim Sehen auch beim Fotografieren statt. Beim Zeichnen und Malen wird sie bewusst angewendet. Vasarely 's Op-Art ist aber keine traditionelle Malerei. Bei denjenigen Werken, auf die ich mich beziehe, ordnet er in der Ebene gleiche einfache geometrische Formen aneinander, die er lediglich in ihrer Größe variiert und verzerrt. Seine Arrangements aus einfachen Formen erhalten auf diese Weise ein beeindruckendes räumliches Aussehen.

Ich habe die Beschränkung auf einfache Formen übernommen, die Formen sind aber dreidimensional. Statt z.B. Kreisen verwende ich Kugeln, die zudem nur in ihrer Größe variieren. Die bereits gewonnene Dreidimensionalität lässt sich so noch steigern. Beim Kugel-Trichter ändere ich deren Größe "monoton" in Richtung zur Mitte, wo sie eigentlich zu Null werden sollte, um unendliche Ferne anzudeuten. Die realistische Beschränkung (sehr kleine Kugeln sind kaum noch zu handhaben und bald nicht mehr zu sehen) mache ich abrupt mit einer mittigen Kugel aus einem anderen Material im kleinsten angewendeten Durchmesser (Abb.3).

Abb.4 ein weiterer Kugeltrichter mit Wänden, die an Vasarely 's Museum in Aix en Provence erinnern
Abb.5 Vasarely 's Museum in Aix en Provence

Einen zweiten Kugel-Trichter fertigte ich in "klassischer" 6er-Teilung mit auf ebener Unterlage liegenden Kugeln an (Abb.4). Damit die Kugeln nicht wegrollen, umgrenzte ich das Arrangement mit gelochten Wänden. Unbewusst wiederholte ich die Bienenwaben-Struktur und die kontrastierenden Kreisflächen darauf, die Vasarely 's Museum in Aix en Provence äußerlich ausmachen (Abb.5). Diese Verbindung bemerkte ich aber erst, als ich das Museum kürzlich zum ersten mal besuchte.

3. Ein Kugel-Kissen  ↑ Anfang

Dieses Kugel-Arrangement ist nur zu Anschauen gemacht, es hat keinen anderen Zweck. Eine direkte Ähnlichkeit mit einem Bild von Vasarely besteht nicht. Am ehesten wäre Tupa-2 zu nennen, wenn man eine der drei Rhomben als Würfel-Fläche deutet (Abb.7). Darin wären Kreis-Flächen in zwei zueinander senkrechten Richtungen in der Größe variiert und verzerrt. Mein dreidimensionales Kugel-Kissen enthält lediglich verschieden große Kugeln.

Abb.6 Kugel-Kissen in Draufsicht.                                           Abb.7 Bild Tupa-2 von Vasarely

4. Kugel-Übungsstücke  ↑ Anfang

4.1 Kugelpackungen  ↑ Anfang

Abb.8 Tetraeder aus dicht gepackten Kugeln (an einen Kanonenkugelhaufen auf einem alten Burghof erinnernd)

Beim Uhren-Zifferblatt spielte die dichtest mögliche Kreispackung in der Ebene eine Rolle. Man kann damit nur das gleichseitige Dreieck so dicht ausfüllen. Ein Quadrat (allgemein: ein Rechteck) lässt sich von allen Rändern her betrachtet mit Kreisen nur "verdünnt" gleichmäßig füllen. Das geschieht in der Anordnung, von der in Vasarely 's Bild Vega-Tek ausgegangen wurde. Im Inneren eines Tetraeders existiert vermutlich auch eine dichteste, hier eine Kugelpackung. Angedeutet wird das dadurch, dass auf deren Seitenwänden das Muster der dichtest möglichen Kreispackung in der Ebene erscheint (Abb.8).

Abb.9 Würfelförmig begrenzte Kugelpackung,
          Ansichten auf zwei in der Raumdiagonale gegenüber liegende Würfelecken

Nachtrag (April 2020)
Beide Vermutungen haben sich bestätigt: siehe Dichteste Kugelpackung

4.2 Kugel mit Sonnen-Sektor   ↑ Anfang

Die Kugel-Oberfläche stellt die Himmels-Sphäre dar. Die obere Hälfte ist der sichtbare, die untere der unsichtbare Teil. Die trennende Ebene ist der Horizont eines irdischen Beobachtungsortes. Ausgeschnitten ist derjenige Sektor, den die Sonne insgesamt über den Tag und übers Jahr einnimmt. Im Mittelpunkt befinde sich der Beobachter. Da die Erde im Vergleich zu ihrer Entfernung von der Sonne (entspricht dem Radius der Beton-Kugel) vernachlässigbar klein ist, lassen sich in diesem Punkt alle Beobachter auf der Erde versammelt vorstellen. Aber nicht alle haben denselben Horizont, und für die Hälfte befindet sich die Sonne unter dem Horizont. Die blaue Kugel im Zentrum symbolisiert die Erde in übermässiger Vergrösserung.

4.3 Kleine Planetariums-Kugel  ↑ Anfang

Die Oberfläche der von den Drähten angedeuteten Kugel repräsentiert die sich um die Erde drehende Himmels-Sphäre. Die Drähte stellen Meridiane und Breitenkreise auf ihr dar. Hinzugefügt ist die von den Wendekreisen berührte Jahresbahn der Sonne (Ekliptik-Kreis). Die Kugel ist an ihrem südlichen Ende abgeschnitten. Weggelassen ist der Teil des Himmels, der bei uns (Bern/CH; geographische Breite 47° Nord) zu keiner Zeit sichtbar ist. Im gegenüber liegenden Teil rund um den Nordpol des Himmels befinden sich die zu jeder Jahreszeit sichtbaren Himmelskörper (zirkum-polare Sterne).

Die Planetariums-Kugel ist mit angehefteten Stern-Symbolen als auch von innen zu betrachtender Stern-Globus verwendbar. Hauptsächlich dient sie als Beobachtungshilfe. In ihrer Mitte befindet sich eine kleine Kugel, mit deren Hilfe sich durch Peilung die Position eines Sternes auf der Gitterstruktur der Kugel ablesen lässt. Mit den abgelesenen Koordinaten ist dann der Stern in einem Sternatlas identifizierbar. Die Kugel muss der Drehung des Nachthimmels nachgeführt werden. Eine einfache Methode ist, ein Symbol eines Leit-Sterns (vorzugsweise Sirius), der ohne Hilfe gefunden werden kann, auf der Kugel anzuheften. Die Kugel und ihre Öffnung sind groß genug, um sich mit Kopf und Oberkörper in ihr aufhalten zu können. An der Öffnung ist die Kugel drehbar gelagert: flacher Ring auf 3 Kugellagern liegend und am Innenrand mit 2 Kugellagern radial geführt.

4.4 Wasser-Kugeln  ↑ Anfang

Regentropfen:
mit Wasser gefüllte durchsichtige Plastikkugel (Durchmesser 8 cm) als Großmodell eines Regentropfens:
siehe auch den Artikel "Wie entsteht ein Regenbogen?"

Die Kugel-Form der fallenden Regentropfen ist indirekt Ursache für die Kreis-Form des Regenbogens. In jeden einzelnen Tropfen dringt das Sonnenlicht ein und wird von seiner Rückseite als Lichtkreis konzentriert reflektiert. Beim Eindringen und Verlassen des Tropfens wird das Sonnenlicht zudem in die "Regenbogenfarben aufgebrochen". Der austretende Lichtkreis besteht aus mehreren farbigen ineinander liegenden Kreisen. Vom Lichtkreis jeden einzelnen Tropfens sieht der Beobachter nur einen winzigen Punkt in einer der Regenbogenfarben. Der ebenfalls als Kreis sichtbare Regenbogen ist die Summe der unzählbar vielen farbigen Punkte von unzählbar vielen Regentropfen. In Umfangsrichtung besteht er aus Punkten gleicher Farbe, aber in radialer Richtung steuern nicht weit entfernte Regentropfen bereits einen Punkt einer anderen Farbe bei, die sich momentan höher befindenden Rot, die tieferen Blau.

Kugellinse:
mit Wasser gefüllte durchsichtige Plastikkugel (Durchmesser 8 cm) im Inneren einer Plastikkugel (Durchmesser 16 cm) als Globus-Sonnenuhr zur Abbildung der Sonne als Licht-Zeiger
siehe auch den Artikel "Eine Reflex-Globus-Sonnenuhr"

<< Abb.10 Globus-Sonnenuhr mit Schusterkugel im Inneren
In Bern λ=7,5°; φ=47° ist es 9:40 Uhr (Wahre Ortszeit)
Westlich von Madagaskar steht die Sonne senkrecht (Mitte Januar)

Beim Regentropfen wird auf der Rückseite nur ein kleiner Teil des eingedrungenen Lichtes reflektiert. Das meiste geht hindurch und wird hinter dem Tropfen konzentriert. Das ist für das Phänomen Regenbogen ohne Bedeutung, jedoch nicht in der Technik. Das Licht wird zwar nicht so scharf im Brennpunkt gesammelt wie bei einer optischen Linse, für einfache Anwendungen genügt aber die erreichbare Konzentration. Von alters her ist die Schusterkugel bekannt, ein mit Wasser gefülltes kugelförmiges Glas, mit dessen Hilfe ein größerer Teil des Kerzenlichts auf dem Arbeitsgegenstand konzentriert werden konnte. Ich habe eine Schusterkugel als Kugellinse im Inneren einer kugelförmigen Sonnenuhr (die zur Hälfte transparente Kugel ist zugleich Globus) angebracht, mit der ich die Sonne auf dem kugelförmigen Zifferblatt als Uhrzeiger abbilde. Der Lichtfleck zeigt außerdem an, wo die Sonne gerade senkrecht auf die Erde trifft (Abb.10). Eine optische Linse müßte ich der Sonne, die sich über den Tag auf etwa einem halben Kreisbogen am Himmel bewegt, nachdrehen. Eine Kugel ist eine Linse ohne fixe optische Achse, sie funktioniert in allen Richtungen.

Siegfried Wetzel, CH 3400 Burgdorf, November 2010 (Dez.10, März 16, April 20)

 ↑↑ Anfang
<< Home
<< anderes Geometrisches