<< Home
<< andere Farbe-Beiträge
 ↓↓ Ende

Wie entsteht ein Regenbogen?
Die Geschichte seiner Erklärung seit Descartes

Zusammenfassung

Versuche, die Entstehung des Regenbogens zu erklären, wurden bereits in der Antike (Arisoteles) unternommen. Im Mittelalter gab es die ersten Experimente an einer mit Wasser gefüllten Kugel als Modell eines Regentropfens (Dietrich von Freiberg/Sachsen). Im 17. Jahrhundert knüpfte René Descartes daran an und gab eine Erklärung ab, die auch heute noch in erster Näherung gültig ist. Sie bezog sich allerdings nur auf die Entstehung eines am Himmel sichtbaren hellen Bogens. Dessen Farbigkeit blieb vorläufig noch ein Rätsel, das aber schon bald von Newton prinzipiell gelöst wurde. Die uns heute bekannte Erklärung aller am Himmel sichtbarer farbiger Bögen einschließlich der sogenannten "überzähligen" Regenbögen wurde im 19. Jahrhundert gefunden, als das alte Wellenmodell von Huygens (17. Jahrhundert) endlich auf die Ausbreitung des Lichts angewendet wurde. Parallel zur physikalischen Beschreibung erfolgte in gegenseitiger Befruchtung ein intensiver Fortschritt bei der Erarbeitung entsprechender mathematischer Methoden durch Airy (30er Jahre des 19. Jahrhunderts) und Mie (Beginn des 20. Jahrhunderts). Die wissenschaftliche Behandlung des Regenbogens half aber nicht nur, die Natur des Lichts sondern auch die gegenseitige Beeinflussung kleinster bewegter Teile der Materie - deren sogenannte "Regenbogen-Streuung" - zu verstehen.

Inhalt

1. Einleitung
2. Entstehung eines farblosen Regenbogens
3. Entstehung der Regenbogen-Farben
4. Entstehung des Nebenregenbogens
5. Entstehung der "überzähligen" Regenbögen
6. Der Regenbogen der Mathematiker
7. Der Regenbogen der Wissenschaftler
   7.1 Descartes: Philosoph, Naturwissenschaftler und Mathematiker
   7.2 Die Regenbogen-Streuung der Physiker
   7.3 Halbklassische Physik
8. Literatur (inklusive Bildnachweise)
9. Anmerkungen

Abb.1 Regenbogen-Garnitur: Hauptregenbogen mit inneren "überzähligen" Regenbögen und äußerem Nebenregenbogen, [11]

1. Einleitung  ↑ Anfang

Descartes (1594-1650) lieferte die älteste, mehrheitlich auch heute gültige Beschreibung des Regenbogens. Seine Erklärung gilt aber nur für die Position des Regenbogens am Himmel und für seine Kreisförmigkeit. Wie das Auffallendste am Regenbogen - nämlich seine Farben - entstehen, hat aber schon Newton etwa 30 Jahre später (1642-1727) prinzipiell angegeben.

Der Grund für die innere Verbreiterung des Regenbogens in Form schwacher "überzähliger" Bögen wurde hingegen erst erkannt, als außer der bisherigen Strahlenoptik auch die Wellenoptik beigezogen wurde. Als bedeutende und allgemein befriedigende wellenoptische Untersuchungen gelten die Arbeiten von Potter, Airy und Miller, die diese in der Mitte des 19.Jahrhunderts durchführten.

Der mitunter zusätzlich erkennbare schwächere Nebenregenbogen ist gleich wie der Hauptregenbogen erklärbar. Es ist lediglich zu beachten, dass das Licht in diesem Fall 2 mal, anstatt nur 1 mal in den einzelnen Regentropfen reflektiert wird, und dass sich dabei die Reihenfolge der Farben umkehrt.

2. Entstehung eines farblosen Regenbogens  ↑ Anfang

Man kann für die Regentropfen die reine Kugelform annehmen. Dem entsprachen bereits die ersten bekannten Regenbogenexperimente, die Dietrich von Freiberg (13. und 14. Jahrhundert, [1, ab S.110]) und De Dominis (1610) mit Hilfe einer mit Wasser gefüllten Glaskugel vornahmen. Descartes wiederholte diese Versuche, war darüber hinaus aber der Erste, der den Regenbogen geometrisch, das heißt mit strahlenoptischem Modell konstruierte [1, ab S.200)].

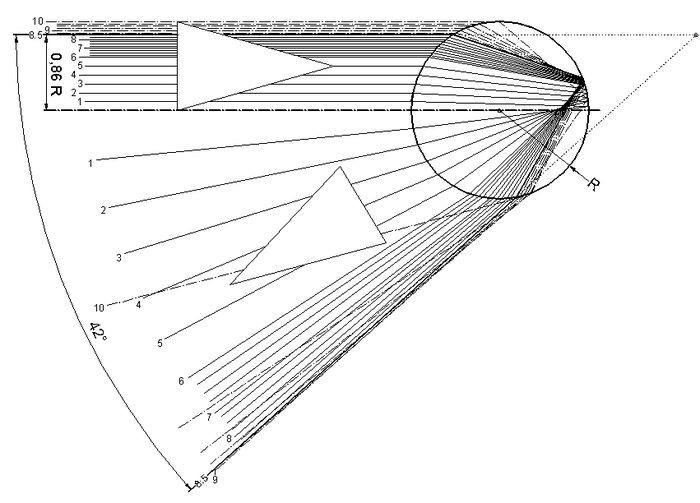Abb.2 Strahlengang nach Descartes in einem Wassertropfen, monochromatisch, untere Hälfte der einfallenden Strahlen ist weggelassen, vgl. [10, S.422], Anmerkung 1

Dabei spielt die Grösse der Tropfen (Durchmesser) keine Rolle. Descartes verfolgte akribisch eine grosse Zahl von Sonnenstrahlen auf ihrem Weg durch einen Tropfen. Für die Brechung wendete er das von Snelius einige Jahre vorher formulierte Gesetz an. Dass die Regenbogenfarben auch eine Folge der Dispersion, nämlich der Wellenlängen-abhängigen Brechung sind, war ihm nicht bekannt. Seine diffuse Vorstellung, wie die Farben in den Tropfen entstehen, erwies sich später als untauglich. Er verwendete für das gesamte Sonnenlicht einen einzigen Brechungsindex, den Wert n=1,33 (=4/3).

Descartes beschäftigte sich zuerst mit dem Hauptregenbogen, beachtete nur die einmalige Reflexion an der Tropfenrückseite und den folgenden Austritt der Strahlen etwa wieder in Richtung zur Sonne (Abb.2). Es erwies sich, dass außermittige Strahlen zunächst mehr und mehr seitlich gestreut werden, die Umlenkung aber 138,5° (180° Umlenkung heißt in sich selbst zurück geworfen) nicht unterschreitet. Die weiter am Rand des Tropfen eintretenden Strahlen werden wieder weniger gestreut. Descartes näherte sich dem Grenzwert, indem er die Dichte der untersuchten Strahlen in seiner Nähe verzehnfachte. Gleich wichtig war die Erkenntnis, dass das meiste Licht (die meisten Strahlen) in der Nähe des Grenzwinkels konzentriert ist.

Jeder Regentropfen wirft einen Teil des Sonnen-Lichtes als Kegel-förmigen Spot zurück (Abb.3a). Die Grundhelligkeit des Regen-Himmels stammt zunächst vom Licht, das von der Vorderseite der Tropfen diffus reflektiert wird. Ihm werden die Spot-Lichter addiert. Da das meiste Licht in ihren Mänteln konzentriert ist, sorgen diese Kegel-förmigen Spot-Lichter für eine deutliche örtliche Aufhellung des Himmels, die als Regenbogen zu erkennen ist.

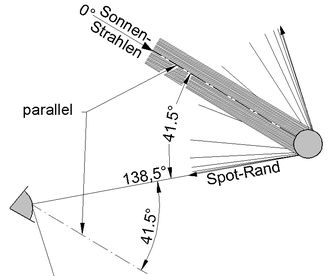
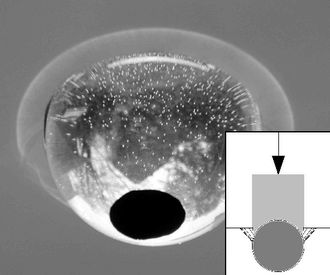Abb.3a Nur der unterste Licht-Strahl aus einem Regentropfen erreicht den Beobachter und ist Mantellinie sowohl des Kegel-förmigen Spots (schematisch gezeichnet) als auch des Regenbogen-Kegels, in dessen Spitze sich der Beobachter befindet.
Abb.3b Heller Rand des aus einer Wasser-gefüllten Glaskugel tretenden Kegel-förmigen Spots, monochromatisch [eigenes Experiment]

Der Kegelwinkel der kleinen Spot-Lichter ist etwa 2 mal 41,5° (41,5°=180°-138,5°) groß. Der Regenbogen erscheint einem Beobachter als Teil eines Kreises unter einem Seh-Winkel von ebenfalls 2 mal 41,5° (Abb.3a). Der Beobachter sieht einen hellen Bogen, der aber nur aus je einem Strahl unzählbar vieler Spots zusammen gesetzt ist (s.a. Abb.6). Jeder Einzel-Strahl ist wiederum nur einer von vielen, die den Spot-Mantel ihres Tropfens bilden.

Im Inneren des Regenbogen-Kreises wird dem Himmel das schwache Licht aus dem Inneren der Spot-Lichter zusätzlich zur Grundhelligkeit beigefügt. Diese schwache Aufhellung wird im Vergleich zum Himmel ausserhalb des Regenbogen-Kreises bemerkt. Der Beobachter kann nämlich nicht ins Innere der sich aussen befindenden Spot-Lichter schauen.

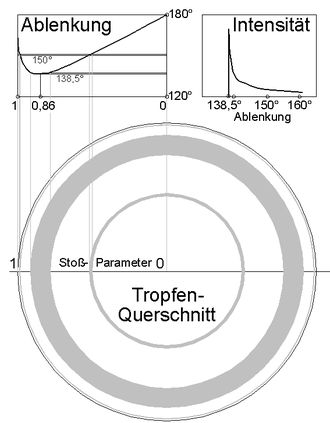<< Abb.4 Licht-Verstärkung im Spot-Mantel nach Descartes, [9]

Die Konzentration des Lichtes (Licht-Verstärkung) in den Spot-Mänteln ermittelte Descartes mit einer relativ groben Methode. Er unterteilte die Ablenkung in viele kleine Intervalle und stellte dann fest, aus welchem Ring der einfallenden Sonne das Licht eines Intervalls stammt. Die Intensität in jedem Intervall ist der zugehörenden Ringfläche proportional. Abbildung 4 zeigt, dass das Licht im Grenzintervall 139,5° bis 138,5° aus einem sehr breiten Ring stammt. Von 151° bis 150° Ablenkung zum Beispiel stammt das Licht aus zwei sehr schmalen Ringen beidseits des breiten Rings mit mittlerem Stoß-Parameter 0,86 (Stoßparameter = relativer Tropfen-Radius = 0 ... 1).

3. Entstehung der Regenbogen-Farben  ↑ Anfang

Das Regenbogen-Modell von Descartes erfährt bei Beachtung der von Newton beschriebenen Wellenlängen-abhängigen Brechung des Lichts nur eine einfache Änderung, mit der es aber in der Lage ist, die faszinierende Farbigkeit des Regenbogens zusätzlich zu erklären.

Der Brechungsindex der verschiedenen Wellenlängen variiert leicht um den Wert 1,33 (Wasser). Anstatt eines einzigen Kegel-förmigen Spots gibt es für jede Spektralfarbe des Sonnenlichts einen Spot mit je einem anderen Kegelwinkel (Abb.5a). Alle Kegel stecken ineinander (haben annähernd die gleiche Spitze). Der grösste Kegel ist der rote. Sein Mantel ist von den anderen Kegeln nicht überlagert, zu Rot wird keine andere Farbe addiert. Der nächst kleinere ist orange. Im Bereich seines Mantels hat der rote Kegel nur wenig Licht, so dass Orange wenig verwaschen wird. Beim innersten Kegel - dem violetten - werden im Mantelbereich alle schwachen anderen Farben überlagert. Violett ist am stärksten verwaschen, ist aber noch dominant. Im Inneren der Kegel addieren sich alle gleich schwache Farben zu schwachem Weiß.

Das schwache Weiß erhellt den Himmel im Inneren des Regenbogen-Kreises, wie oben bereits beschrieben ist. Aus dem bisher behandelten fiktiven unbunten "Regenbogen" wird der bekannte farbige Regenbogen. Der Kegelwinkel der Spots bzw. der Seh-Winkel des Regenbogens hat für die Farbe Violett den Wert 2 mal 40,6°, für Rot den Wert 2 mal 42,4° (Descartes gab einheitlich 2 mal 41,5° an).

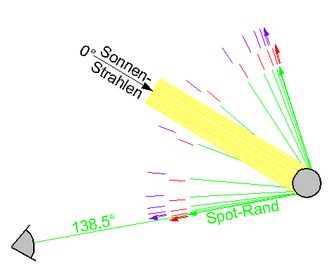
Abb.5a Farbige Version von Abb.3a: Nur ein farbiger Licht-Strahl pro Regentropfen erreicht den Beobachter, jeder anders-farbig empfangene Strahl stammt von einem sich momentan höher oder tiefer befindenden Tropfen.
Abb.5b Farbige Version von Abb.3b: Farbiger Rand des aus einer Wasser-gefüllten Glaskugel tretenden Kegel-förmigen Spots [eigenes Experiment]

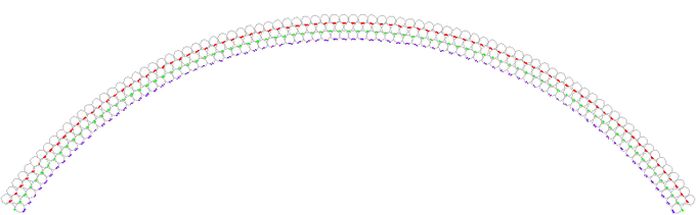
Abb.6 Regenbogen aus drei Hauptfarben, schematisch gebildet aus je einem einzigen Lichtstrahl, je aus einem von vielen Regentropfen stammend

Der Regenbogen in Abbildung 6 enthält in jeder Bogenreihe in Wirklichkeit etwa zehn- bis hundert-tausend (abhängig vom Abstand) mal mehr entsprechend kleinere Tropfen. Das Bild ist eine Momentaufnahme, denn die Tropfen fallen. Sie sind auch in keiner Weise regelmäßig zueinander angeordnet; im Großen wird dennoch eine stehende und bogenförmige Lichterscheinung gesehen, die zudem geschlossen farbig, brillant und weniger breit ist (vgl. Abb.1).

4. Entstehung des (ersten) Nebenregenbogens  ↑ Anfang

Descartes konstruierte auch einen farblosen Nebenregenbogen. Beim Hauptregenbogen wird derjenige Teil des Sonnenlichtes gesehen, der die Tropfen nach 1-maliger innerer Reflektion verlässt. Der andere Teil des Lichtes wird erneut reflektiert und verlässt - wiederum nur zum Teil - an einer anderen Stelle die Tropfen.

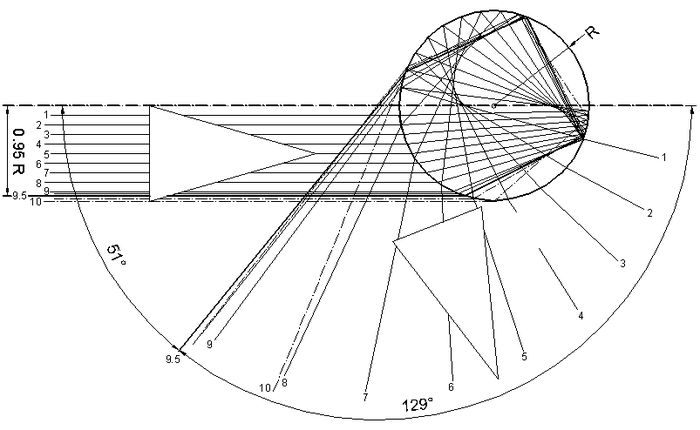Abb.7 Strahlengang nach Descartes in einem Wassertropfen beim Nebenregenbogen nach 2-maliger innerer Reflektion, monochromatisch, obere Hälfte der einfallenden Strahlen ist weggelassen, vgl. [10, S.422], Anmerkung 1

Mit diesem Licht wird ein erster Nebenregenbogen sichtbar. Weil das in den Tropfen verbleibende Licht nach jeder Reflektion schwächer wird, ist der erste Nebenregenbogen der einzige, der von einem Beobachter identifiziert werden kann (Anmerkung 2). Der Hintergrund der Regenwolke muss dafür besonders dunkel sein.

Der mittlere Strahl verlässt den Tropfen mit 360° Umlenkung nach hinten. Die seitlich in den Tropfen eintretenden Strahlen werden weiter als beim Hauptregenbogen gestreut. Die Ablenkung sinkt nach Descartes bis auf 232° (Violett: 233,6°, Rot: 230,3°) und vergrößert sich dann wieder. An diesem Grenzwinkel ist die Intensität des austretenden Lichts auch am höchsten. Es sind mit der Sonne nach hinten strahlende Weitwinkel-Spots entstanden. Ihre Kegelwinkel sind mit 2 mal 128° (Descartes: 128°=360°-232°) übergroß, was aber ermöglicht, dass das in den Kegel-Mänteln konzentrierte Licht den auf der Sonnenseite postierten Beobachter erreichen kann. Der zu 2 mal 180° komplementäre Spotwinkel bzw. der Seh-Winkel des Nebenregenbogens hat bei Descartes den Wert 2 mal 52° ( 52°=180°-128°). Der Nebenregenbogen wird höher als der Hauptregenbogen (Sehwinkel 2 mal 41,5°) gesehen.

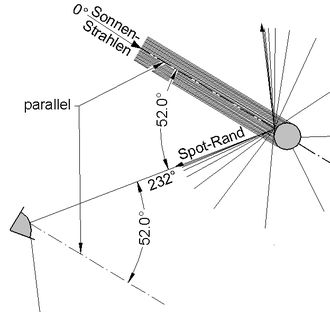
Abb.8a Nebenregenbogen: nur der unterste Licht-Strahl aus einem Regentropfen erreicht den Beobachter und ist Mantellinie sowohl des Kegel-förmigen Spots (schematisch gezeichnet) als auch des Regenbogen-Kegels, in dessen Spitze sich der Beobachter befindet.
Abb.8b Nebenregenbogen: Farbiger Rand des aus einer Wasser-gefüllten Glaskugel tretenden Kegel-förmigen Spots, (vgl. Abb.5b) [eigenes Experiment]
außen: 2 Hauptregenbogen (Verdopplung wegen endlicher Wanddicke der Kugel)

Die Reihefolge der Farben ist wegen der umgekehrten Strahlrichtung der Spots im Vergleich zum Hauptregenbogen vertauscht. Die Seh-Winkel-Differenz ist wegen des längeren Lichtwegs im Tropfen grösser: 2 mal 3,3° (Hauptregenbogen: 2 mal 1,8°).

Beim Nebenregenbogen addieren sich die Farben im Inneren der Spot-Lichter ebenfalls zu schwachem Weiß. Es ist nochmals schwächer als beim Hauptregenbogen und fällt ausserhalb des Nebenregenbogen-Kreises z.T. nach vorn, im wesentlichen aber nach hinten in die Regenwolke hinein. Aus dem Kreis-Ring zwischen den beiden Bögen erreicht den Beobachter kein Spot-Licht von den Tropfen. Dieser Bereich heißt Alexanders dunkles Band, weil der Grieche Alexander von Aphrodisias an der Wende vom 2. zum 3. Jahrhundert diese relative Dunkelheit schon beschrieben hat (ohne dass er eine Erklärung dafür angeben konnte) [1, S.64].

5. Entstehung der "überzähligen" Regenbögen  ↑ Anfang

Die Regenbögen werden bei genauem Hinsehen und bei dunklem Himmel auf der violetten Seite von schmalen, sogenannten "überzähligen" Regenbögen begleitet (s.Abb.1). Ihre Ursache wurde erst im 19. Jahrhunderts erkannt, als man die etwa 1650 von Huygens begründete, 1802/03 von T.Young zum Durchbruch verholfene Wellenoptik auf den Regenbogen anwendete. Ein besseres, nämlich ein Wellen-optisches Modell für die Licht-Verstärkung in den Kegel-Mänteln der Tropfen-Spots ermöglichte nicht nur die Erklärung der "überzähligen" Regenbögen, sondern wirkte sich auch auf die Deutung der "ordentlichen" Bögen (Haupt- und Nebenregenbogen) aus.

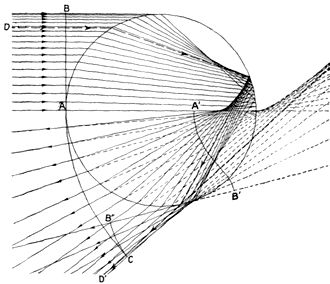<< Abb.9 (Vgl. auch Abb.13) Ein doppelt gekrümmter Wellenzug (A'-B') verlässt den Regentropfen; der Beobachter nimmt das von ihm verursachte Interferenzmuster wahr. [3, Fig.174, S.481]

Dass die gebündelt aus dem Tropfen tretenden Wellenstücke untereinander in ihrer Phase infolge ihres unterschiedlich langen Wegeanteils im Tropfen verschoben sind, erkannte schon T. Young, wurde aber erst von R. Potter (1799-1886, Anmerkung 3) intensiv untersucht. Er folgerte, dass die "überzähligen" Regenbögen Bestandteile des eigentlichen Regenbogens sind.

Potter stützte sich auf die von Airy (1801-1892, Anmerkung 4) für die Behandlung des Regenbogens erarbeitete quantitative Methode (1836). Das in Potters 1838 veröffentlichter Arbeit enthaltene Diagramm (Abb.10b) zeigt anstatt der von Descartes angegebenen monoton abnehmenden (Abb.10a) eine ausschwingende Intensität, die bereits in den Zwischenräumen zu null wird. In ihnen haben sich die in gemeinsame Ablenkrichtung gehenden Wellenstücke gegenseitig ausgelöscht. Den eigentlichen Regenbogen macht der erste, relativ hohe Berg aus. Er hat sein Maximum bereits etwas vor dem Descartes'schen Grenzwinkel, endet andererseits etwas dahinter. Die niedrigeren Intensitäts-Berge werden als "überzählige" Regenbögen gesehen. In der Abbildung ist auch eine von Young angegebene Intensitätskurve enthalten, die zwar gewellt ist, sich aber noch asymptotisch dem Descartes'schen Grenzwinkel nähert. Abb.10a zeigt die nicht mögliche Übertragung der von Descartes angenommenen Intensitätsverteilung auf Wellen, beispielsweise auf Wasserwellen.

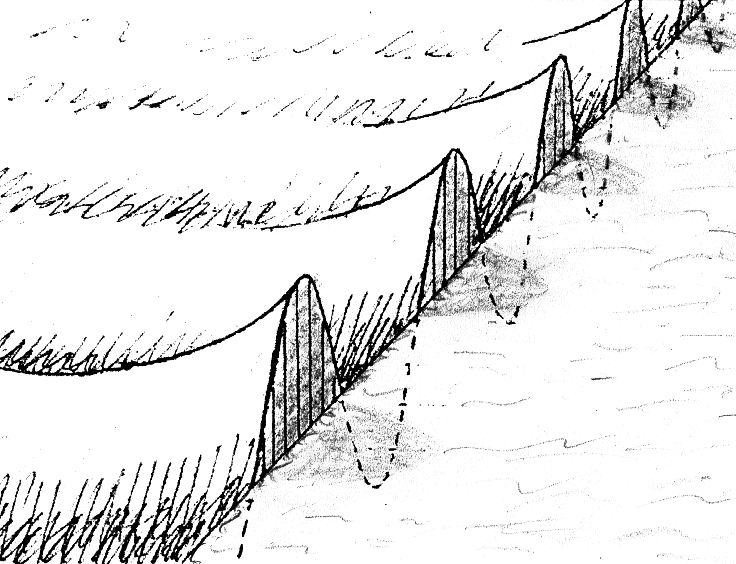
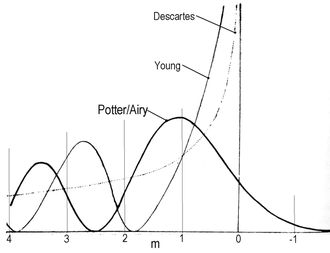Abb.10a Die von Descartes angenommene Intensitätsverteilung ist auf Wellen nicht übertragbar: z.B. ist ein scharfer Übergang zwischen einem welligen und einem ruhigen Teil einer Wasseroberfläche - wie gezeichnet - nicht möglich. [12]
Abb.10b Die von Potter angegebene Licht-Intensität in der Umgebung des Descartes'schen Grenzwinkels, schematisch (Skalierung der Abszisse gilt nur für Rechnung nach der Airy-Methode, Anmerkung 4) [1, S.303]

Im Interferenzmuster der verschiedenen Farben hat nur jeweils der erste Berg seinen eigenen Platz. Die kleineren Berge überlagern sich, wobei durch additive Mischung neue Farben entstehen können. Dass die erhaltenen Muster auch von der Tropfen-Grösse abhängen, erklärt, warum nicht alle Regenbögen gleich aussehen. Bei Verkleinerung der Tropfen-Durchmesser werden die Muster weiter. Das führt dazu, dass die Farbe der "überzähligen" Regenbögen variiert, aber auch dazu, dass der eigentliche Regenbogen breiter und verwaschener wird. Bei sehr kleinen Tropfen (Nebel) mutiert der Regenbogen zu einem weißen Band, weil die Intensitäts-Muster der Farben gleiche Geometrie angenommen haben, was in der Addition Weiß ergibt (Abb.11).

Abb.11 Die Regenbogenfarben als Funktion der Tropfengrösse [4, Fig.14]

W.H. Miller (1801-1880) war der erste, der in entsprechenden Experimenten eine grosse Zahl von "überzähligen" Regenbögen nicht nur sichtbar machte, sondern diese auch vermaß. Er konnte damit die theoretischen Arbeiten von Potter und Airy und die Regenbogen-Beobachtungen umfassend bestätigen.

Seit etwa 1865 wird Licht als elektromagnetische Welle aufgefasst und neben anderen elektromagnetischen Wechselwirkungen mit Hilfe der von James Clerk Maxwell dafür formulierten Gleichungen dargestellt. Gustav Mie hat 1908 die Streuung elektromagnetischer Wellen an sphärischen Objekten beschrieben. Die einfallende ebene Welle wird in "Partialwellen" (s.u.) zerlegt. Für jede Partialwelle wird der Weg innerhalb und außerhalb der streuenden Kugel untersucht, anschließend werden die Anteile der Partialwellen im Beobachtungspunkt addiert. Für die Verhältnisse beim Regenbogen sind einige tausend Partialwellen, von denen jede einzelne bereits ein langer Ausdruck ist, nötig. Die Lösung durch Mie ist exakt, während die durch Airy zum Beispiel auf Annahmen (Verteilung der Lichtintensität in der gekrümmten Wellenfront) angewiesen ist. Allerdings ist eine vollständige Rechnung nach Mie erst mit Hilfe der seit etwa 1990 zur Verfügung stehenden elektronischen Gross-Rechner möglich. Raymond R. Lee, Jr. konnte mit deren Hilfe vergleichende Rechnungen anstellen und die ausreichende Näherung nach der Methode Airy's nachweisen (veröffentlicht 1998, [4], s. Abb.11).

6. Der Regenbogen der Mathematiker  ↑ Anfang

Die erweiterte Behandlung des Regenbogens (der "überzähligen" Regenbögen) mit einer "höheren" physikalischen Theorie (der Wellentheorie des Lichts) verlangte auch bessere quantitative Modelle (mathematische Methoden) zur Beschreibung. Am Regenbogen befruchteten sich Physik und Mathematik gegenseitig. Seit den Arbeiten von Airy, endgültig seit denen von G. Mie kann u.a. auch vom "Regenbogen der Mathematiker" [1] gesprochen werden.

Bei der Berechnung der Lichtintensität in der Nähe des Descartes'schen Grenzwinkels benutzte Airy ein Integral, das verallgemeinert als Airy-Integral (Anmerkung 4) zur Lösung der Airy-Differentialgleichung in die Mathematik eingegangen ist.

Obwohl die Behandlung des Regenbogens mit der sogenannten Mie-Streung unanschaulich ist und keine wesentlich genauere Darstellung als bisher erbrachte, hat der dabei eingeführte Begriff "Partialwelle" allgemeine Bedeutung in der Quantenmechanik und als Abstraktum in der Mathematik erlangt.

7. Der Regenbogen der Wissenschaftler  ↑ Anfang

Beziehungen bestehen nicht nur zwischen der Physik des optischen Regenbogens und der Mathematik, sondern auch zu anderen Zweigen der Physik und auch zur Philosophie, weshalb allgemeiner vom Regenbogen der Wissenschaftler gesprochen werden darf.

Descartes schreibt zu Beginn seiner Abhandlung über den Regenbogen: Der Regenbogen ist ein so bemerkenswertes Wunder der Natur [...], dass ich keine geeignetere Materie zu wählen wüsste, um aufzuzeigen, wie man durch die Methode, derer ich mich bediene, zu Kenntnissen gelangen kann [...] .[13]

Seine Methode wird meist ausschließlich als eine philosophische Lehre angesehen und oft unglücklich, und deshalb unverständlich bis missverständlich, auf den Ausspruch Ich denke, also bin ich.[6, S.65] reduziert. Dabei handelt es sich nur um die "erste Gewissheit", auf der seine Arbeitsweise beruhte, und die er unter dem ausführlicheren Titel Bericht über die Methode, die Vernunft richtig zu führen und die Wahrheit in den Wissenschaften zu erforschen, veröffentlichte. Die Reduktion des universellen Wissenschaftlers Descartes in der öffentlichen Wahrnehmung auf einen Philosophen ist auch dadurch verschuldet, dass die Anhänge in den Nachdrucken seiner Methode meistens weggelassen werden [6, s. Bemerkung in 8.]. Sie wird aber in den ursprünglich anhängenden "Essais" (etwa 6-fache Seitenzahl) konkretisiert, also nur mit ihnen zusammen vollständig dargestellt. Auf sie zu verzichten, liess sich im 17.Jahrhundert mit den von den Abbildungen verursachten hohen Kosten entschuldigen, aber heute nicht mehr.

Einer der drei Essais heißt "Les Météors" (zeitgenössische Definition: Die Erscheinungen in der bis etwa zum Mond reichenden Atmosphäre), in dem Descartes über den Regenbogen schreibt ("de l'arc en ciel"; 10 Abbildungen, 2 Tabellen). Er wurde bis 2006 noch nicht einmal ins Deutsche übersetzt [13]. Die Behandlung des Regenbogens zeigt deutlich, welche wissenschaftliche Methode Descartes in die Moderne - hier in die Physik - einführt. Es handelt um weit mehr als um eine vermeintlich reduktionistische Methodologie eines mathematischen Fundamentalisten [13, Seite 10].

Er ersetzt das bisher (Scholastik) gültige teleologische Weltbild des Aristoteles (Ordnung der Welt hat vorhandene, nicht beeinflussbare Zweckursachen) durch ein kausalistisches, in dem eine feste Beziehung zwischen Ursache und Wirkung besteht (wobei allerdings die Herkunft der Ursache unbekannt oder zufällig sein kann). Das Denken darin ist mechanistisch mit der wesentlichen Konsequenz, dass die Kausalität durch Experimente sichtbar gemacht wird. Mit dem Einbezug von Experimenten übernimmt er eine von seinem wenig älteren Zeitgenossen Galileo Galilei erfolgreich begonnene Arbeitsweise.

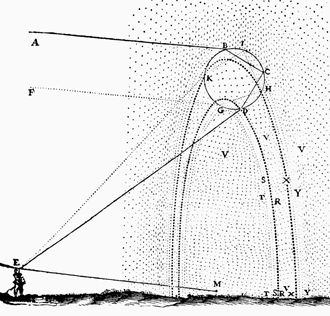<< Abb.12 Zeichnung von Descartes aus "Les Météors" [13, Seiten 218 und 222]

Descartes experimentiert mit einer mit Wasser gefüllten Kugel (verschweigt aber, dass er ihm bekannte ältere und zeitgenössische Versuche wiederholt) und findet mit dem inzwischen bekanntem Brechungsgesetz (dessen zeitgenössischen Entdecker Snelius er nicht erwähnt) auf mechanistische Weise die Lichtkonzentration im Wassertropfen in der unmittelbaren Nähe eines Grenzwinkels für die Ablenkung.

Die abschliessend eingefügte Zeichnung (Abb.12) hat Descartes selbst angefertigt. Sie ist eine spielerische Zusammenfassung seiner Regenbogen-Arbeit (für den Einstieg wenig geeignet). In den Regen-Himmel ist ein übergroßer Tropfen eingezeichnet, der gerade so groß gewählt ist, dass die Haupt- und Nebenregenbogen ausmachenden Lichtkonzentrationen vom Beobachter im richtigen Winkelverhältnis gesehen werden.

Heute scheint es keinen Bedarf mehr an besseren Theorien und mathematischen Modellen für den Regenbogen zu geben. So werden z.B. in (makroskopischen) Wassertropfen keine Quanteneffekte vermutet; ihre Fallgeschwindigkeit ist weit von der Lichtgeschwindigkeit entfernt. Aber auch künftige Wissenschaftler brauchen wie alle Menschen das Beobachten der Naturerscheinungen wie die Luft zum Atmen. Deshalb wird auch die wissenschaftliche Behandlung des optischen Regenbogens nicht aufhören [9].

Am wahrscheinlichsten ist die Fortsetzung der Behandlung der sogenannten "Regenbogen-Streuung" kleinster Teilchen (die Mie-Streuung gilt für Teilchen beliebiger Größe). Dieses physikalische Thema ist jünger als die Behandlung des Regenbogens. Es ist so jung wie die Atom- und die Teilchenphysik. Vom Regenbogen entlehnt es den namengebenden Begriff (umgekehrt wurde "Stoßparameter" für die Beschreibung des Regenbogens übernommen), ist aber mit dem Regenbogen nur formal verwandt. Kleine Teile ziehen sich gegenseitig an, wodurch sie von ihrer Bahn abgelenkt werden. Wenn sie sich zu nahe gekommen sind, überwiegt gegenseitiges Abstoßen, so dass ihre Ablenkung nur bis zu einem Grenzwinkel, dem "Regenbogenwinkel" möglich ist, und sie dort auch in höherer Konzentration vorliegen. Das ist die einzige anschauliche Gemeinsamkeit zwischen der Licht-Konzentration durch Wassertropfen und der Teilchen-Streuung durch gegenseitiges Anziehen und Abstoßen. Gar nicht zusammen passt, dass das Licht in die relativ großen Wassertropfen eindringt, die relativ kleinen Teilchen sich aber nicht einmal berühren.

Als klassische Physik bezeichnet man alle physikalischen Theorien, die bis zum Ende des 19. Jahrhunderts ausgearbeitet wurden. Das sind die klassische Mechanik, die Elektrodynamik, die Thermodynamik und die Optik. Quantenmechanik und Relativitätstheorie sind die Moderne Physik, die die Klassische Physik ergänzt. Um eine Brücke zwischen beiden Teilen zu schlagen, wird oft der Begriff Halbklassisch (oder Halbklassische Physik) gebraucht und als Beispiel dafür der Regenbogen genannt. Im besonderen soll damit eine Abgrenzung zur Physik Newtons hergestellt werden, indem betont wird, dass dem Licht und dem Regenbogen sowohl Wellen- als auch Teilchen-Natur zuzuordnen ist. Andererseits kann auf rein quantenmechanische Betrachtungen verzichtet werden, was immer möglich ist, wenn die Wellenlänge des Lichtes viel kleiner als der Durchmesser der Streuer ist. Das ist bei Regentropfen und sichtbarem Licht der Fall [2, S.82].

8. Literatur (inklusive Bildnachweise)  ↑ Anfang

9. Anmerkungen  ↑ Anfang

Anmerkung 1:   ↑ zurück a)    ↑ zurück b)

Die von Descartes angegebenen Winkel weichen geringfügig von den heute ermittelten ab: Hauptregenbogen: heute 42° anstatt 41,5°,
Nebenregenbogen: heute 51° anstatt 52°.

Anmerkung 2:   ↑ zurück

Das in einem Spot angereicherte drei und vier mal reflektierte Licht verlässt den Tropfen auf der vom Beobachter abgewandten Seite. Fünf mal reflektiertes Licht gelangt wieder zum Beobachter, ist aber zu schwach, jemals mit bloßem Auge erkannt zu werden.

Anmerkung 3:   ↑ zurück

Kurios ist, dass Potter vordergründig das Wellenmodell ablehnte, es aber benutzte und auch die Sprache der Wellentheorie verwendete mit Ausnahme des Worts Welle. So sagte er z.B. luminous surface anstatt wave-front [1, S.297].

Anmerkung 4:   ↑ zurück a)    ↑ zurück b)   ↑ zurück c)

Erklärung an Hand der unten folgenden Abbildung 13 (vgl. auch Abb.9).

Als erstes ist die Form der nach dem Passieren des Tropfens nicht mehr geraden (räumliche Betrachtung: nicht mehr ebenen) Wellenfront zu beschreiben. Airy näherte sie als kubische Parabel y = c·x³ mit Wendepunkt auf dem Descartes'schen Grenzwinkel-Strahl. Um den zweiten Schritt, die Bestimmung des beim Beobachter ankommenden Intensitäts-Bildes des Regenbogen-Lichtes anschaulich zu machen, wird nur ein sehr kleines Stück davon benötigt. Es ist an der Stelle D vergrößert daneben dargestellt. Jeder Punkt der austretenden Wellenfront ist Quelle einer neuen kreisförmigen Welle (Huygens-Prinzip; räumlich: Kugelwelle). In einzelnen Richtungen, die wenig vom Grenzwinkel abweichen, werden die neuen Wellen addiert, wobei für jede dieser Richtungen die beobachtbare Intensität gewonnen wird.

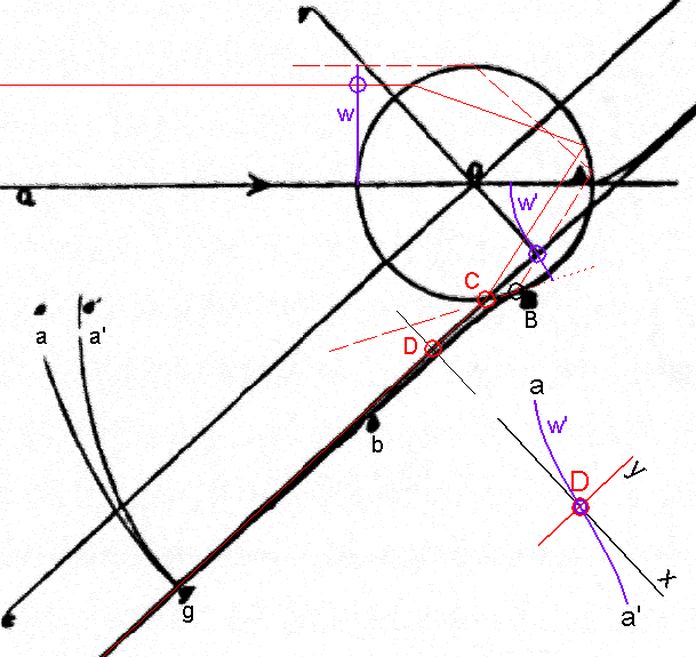Abb.13 Eine doppelt gekrümmte Wellenfront w' mit Wendepunkt verlässt den Regentropfen; der Beobachter nimmt das Ergebnis ihrer Überlagerung wahr. [1, Fig.62, S.299, bearbeitete Zeichnung Potters]
In den meisten Publikationen wird die Front nur virtuell im Tropfen liegend dargestellt, nämlich auf den in ihn hinein gerade verlängerten, schon gebrochen ausgetretenen Strahlen. Außerhalb werden meist ausschließlich und viel zu nahe am Tropfen die beiden spitz zusammenhängenden Äste a und a' gezeichnet (s. z.B. Abb.9). Das ist insofern falsch, weil die Umkehr des Astes a' von konkav zu konvex erst in größerer Entfernung als beendet annehmbar ist. Potter wählte dafür den Punkt g.

 ↑↑ Anfang
<< andere Farbe-Beiträge             Druck-Version (2-spaltig, 12¼ Seiten, *.pdf, 770 kB) >>
<< Home