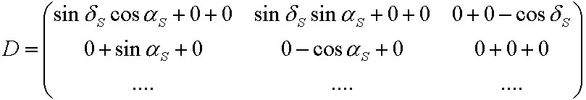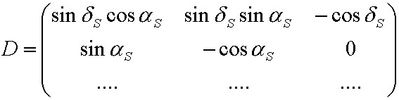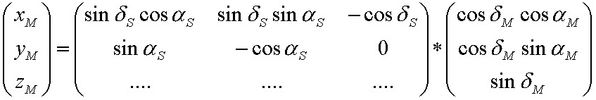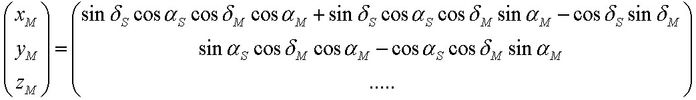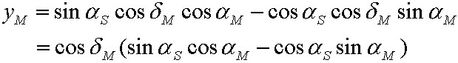<< Home Mondfinsternis und Besselsche Elemente ?siehe auch: Sonnenfinsternis und Besselsche ElementeInhalt
1. Einleitung 1. Einleitung ↑Friedrich Wilhelm Bessel hat seine Theorie nur Erscheinungen gewidmet, bei denen sich der der Erde näherere Himmelskörper zwischen sie und dem entfernteren schiebt [1]. Seine Elemente werden somit typischerweise für die Vorhersage einer Sonnenfinsternis angewendet, wenn sich der Mond zwischen Erde und Sonne schiebt. Eine Mondfinsternis wird von der Erde aus beobachtet, wobei sie von jedem Ort auf der Erdoberfläche aus gleich erscheint. Die einer irdischen Sonnenfinsternis entsprechende Aufgabe wäre, die von einem Beobachtungsort auf der Mondoberfläche zu sehende Verfinsterung der Sonne durch die Erde zu beschreiben. Weil bei der Behandlung von Mondfinsternissen ebenfalls wie bei der von Sonnenfinsternissen primäre astronomische Elemente in die Beobachtung der Finsternisse direkter entsprechende astronomische Elemente durch Koordinatentransformation in ein anderes Koordinatensystem umgerechnet werden und manche mathematischen Ausdrücke der Natur der Sache entsprechend ähnlich aussehen, wird gelegentlich auch von Besselschen Elementen der Mondfinsternisse gesprochen [2]. Diese Redeweise lehne ich entschieden ab. Die Besselschen Elemente sind Zwischengrößen, die erst noch zu den den auf der Erde beobachtbaren Mondschatten beschreibenden geometrischen Größen weiter zu verrechnen sind. Die sogenannten "Mondfinsternis-Bessel-Elemente" sind hingegen die die beobachtete Mondfinsternis direkt beschreibenden geometrischen Ausdrücke, sie sind die Endgrößen. Das Besondere an der Arbeit Bessels war nicht eine bestimmte mathematische Arbeitsweise. Bessel wird im Zusammenhang mit Sonnenfinsternissen (nicht mit Mondfinsternissen !) namentlich nur deshalb gewürdigt, weil er die Idee hatte, die nach ihm benannten Elemente zu formulieren und für weitere Berechnungen zur Verfügung zu stellen. Koordinatentransformationen waren längst bekannt und gehörten zur Tagesarbeit der Astronomen. Bei der Behandlung einer Mondfinsternis findet nicht das zweistufige Verfahren wie bei einer Sonnenfinsternis statt. Es gibt keine Fundamentalebene mit Elementen, die erst in einem zweiten und sehr indviduellen Schritt für die Ermittlung der Erscheinungen an einem bestimmten Ort benutzt werden. Ein solcher Ort existiert nicht auf der Erdoberfläche, denn verfinstert wird der Mond, und das sieht von jedem Ort der Erde aus gesehen gleich aus. Ich werde das allgemein gebrauchte Verfahren, mit dem der Verlauf einer Mondfinsternis beschrieben wird, darstellen und gelegentlich auf rein rechnerische Parrallelen zu den für eine Sonnenfinsternis gebrauchten Besselschen Elementen hinweisen. Im Anhang werde ich auf solche Parallelen verzichten, indem ich nicht zwei Gleichungen von Bessel übernehme und abwandele, sondern diese ohne Bezug auf Rechnungen von Bessel selbst und auf andere, grundsätzlicere Weise (Koordinatentransformationen mit Hilfe Eulerscher Winkel) herleite. 2. Schritte der Beschreibung einer Mondfinsternis ↑2.1 Schattenachse ↑Der Mond verfinstert sich, wenn er in den Schatten, den die von der Sonne beleuchtete Erde in den Weltraum wirft, eintritt. Er verfinstert sich deutlich, wenn er in den Kernschatten der Erde eintaucht. Seine für die Finsternis relevante Bewegung auf die Schattenachse zu beziehen, ist naheliegend. Diese Achse ist eine vom Sonnenmittelpunkt durch den Erdmittelpunkt in Richtung Mond verlaufende Linie und ist mit den Ephemeriden Rektaszension und Deklination (äquatoriale sphärische Koordinarten) der Sonne bereits bekannt. Die bei einer Sonnenfinsternis vorliegende Schattenachse enthält den Erdmittelpunkt nicht, weshalb ihre Richtung aus den Ephemeriden von Sonne und Mond berechnet werden muss. 2.2 Sehwinkel und sphärisches Koordinatensystem ↑Bei einer Mondfinsternis stellt sich die Aufgabe, für die Lage des Mondes auf die Schattenachse bezogene sogenannte "Sehwinkel" anzugeben. In der Schattenachse liegt wie bei der Behandlung einer Sonnenfinsternis zweckmäßig eine Achse des für die Betrachtung nötigen Bezugssystems (Zielsystem). Dafür wird die Polachse eines sphärischen Koordinatensystems gewählt, denn dessen Winkel (sphärische Koordinaten) sind die gewünschten Sehwinkel. Ursprung des Bezugssystems sei auch der Erdmittelpunkt. Die Polachse zeige von der Sonne weg, d.h. zur "Gegensonne" hin. Somit sind ihre sphärischen Koordinaten im äquatorialem Ausgangssystem von den Ephemeriden der Sonne um 180° verschieden (s. Abb.1). Die meisten Beobachter fragen nur nach dem Abstandswinkel zwischen Erdschatten und Mond (erste sphärische Koordinate, Sehwinkel: Poldistanzwinkel), weshalb die Winkellage auf einem Kreis um den Mittelpunkt des Erdschattens (zweite sphärische Koordinate, Sehwinkel: Azimutwinkel) oft nicht angegeben wird (s. Abb.4 u. Abb.5). 2.3 Umrechnung der Mondposition vom Ausgangssystem ins Zielsystem ↑Die Umrechnung zwischen den beiden gegeneinander verdrehten sphärischen Koordinatensytemen (äuatoriales und Zielsystem) erfolgt prinzipiell nicht direkt von sphärischen zu sphärischen Koordinaten, sondern immer mit Einschaltung des Zwischenschritts der Um-/Rückwandlung zu/von kartesischen Koordinaten. Bei der Behandlung einer Sonnenfinsternis mit Besselschen Elementen unterbleibt die Rückwandlung zu sphärischen Koordinaten. Der Abstand der Schattenachse von der z-Achse (gleich Polachse) wird mit zwei Besselschen Elementen (die Gesamtzahl der Besselschen Elemente ist Acht!) in Form der kartesischen x- und der kartesischen y-Koordinate angegeben. Eine umfangreiche Arbeit bei der Umrechnung ist das Aufstellen der Drehmatrizen, die von den kartesischen Koordinaten der Mondposition im Äquatorsystem ausgehen und zu den entsprechenden kartesischen Koordinaten im Zielsystem führen. Sie wird dadurch erleichtert, dass die bei der Ermittlung der Besselschen Elemente für Sonnenfinsternisse verwendeten Drehmatritzen prinzipiell gleiche Formeln sind und somit wieder verwendet werden können. Von Besselschen Elementen selbst bei Mondfinsternissen zu sprechen, ist aber nicht zutreffend. Diese in der Zeit nach Bessel und auch erst nach dem einige Zeit spärter am gleichen Thema arbeitenden US-Amerikaner William Chauvenet entstandene Gewohnheit ist salopp und irreführend, was bei genauerem Hinsehen, das heißt bei mehr als nur rezeptartigem Umgang mit den Besselschen Elementen, schnell deutlich wird. 2.4 Größe des Erdschattens ↑Die Radien von Halb- und Kernschatten der Erde werden wie schon die Richtung zum Mond für den irdischen Beobachter als Sehwinkel angegeben. Genau genommen haben diese Winkel ihren Scheitel im Erdmittelpunkt, aber der Fehler, der durch Beobachtung von der Erdoberfläche aus entsteht, ist vernachlässigbar klein. Die geometrischen Betrachtungen finden zunächst in einer Ebene statt, die die Mittelpunkte der drei beteiligten Himmelskörper Erde, Sonne und Mond enthält (s. Abb.4 u. Abb.5). Dieses Vorgehen ist allgemein und traditionell und auch bei einer Sonnenfinsternis keine Besonderheit, die von Bessel eingeführt worden wäre. Die von ihm bei der Behandlung von Sonnenfinsternissen eingeführte Besonderheit ist die zusätzlich gebrauchte sogenannte Besselsche oder Fundamental-Ebene, die senkrecht zur o.g. Ebene liegt und nur den Erdmittelpunkt enthält. Bei der Behandlung von Mondfinsternissen spielt sie keine besondere Rolle. 3. Berechnung der Mondfinsternisgrößen ↑
3.1 Die Schattenachse als Polachse des Ziel-Koordinatensystems ↑
Die Richtung der Polachse (z-Achse) des Ziel-Kugelkoordinatensystems sind im äquatorialen Koordenatensystems mit den Ephemeriden der Sonne bekannt. Da die positive Polachse (z-Achse) von der Sonne weg zur "Gegensonne" zeigt, ergeben sich ihre äquatorialen Winkel Rektaszension a und Deklination d zu: 3.2 Sehwinkel des Mondes ↑Die kartesische xy-Ebene des Zielsystems ist mit der Besselschen Fundamentalebene identisch, wird aber im Unterschied zu Letzterer weder aus anschaulichen Gründen noch zur weiteren eigentlichen Vorhersage wie bei einer Sonnenfinsternis (Situation an individuellen Orten auf der Erdoberfläche) gebraucht. Bei einer Mondfinsternis sind Winkel (Sehwinkel) das Ergebnis der Betrachtung, also müssen die kartesischen Mond-Koordinaten x und y in Winkel-Koordinaten rückgewandelt werden.
Nachstehend die bekannten Gleichungen für die kartesischen Mond-Koordinaten x und y bei einer Sonnenfinsternis (s. z.B. Gl.n (8) und (9) in meinen eingangs erwähnten Aufsatz):
Im 2. Anhang löse ich mich noch weiter von Bessels Rechenarbeit, indem ich im Bezugssystem die x- und die y-Achse im Vergleich zum Besselschen Fundamentalsystem umgekehrt anordne. 3.3 Sehwinkel der Schattenkreishalbmesser ↑Die Sehwinkel f1 des Halbschattendurchmessers und f2 des Kernschattendurchmessers sind zusätzlich zu den Sehwinkeln der Mondrichtung und des Mondhalbmessers erforderlich, um die verschiedenen Kontakte zwischen Mondrand und den Schattenrändern beschreiben zu können (s. Abschn. 3.4). Ihre Ermittlung ist eine relativ einfache, weil ebene geometrische Aufgabe. Drei Punkte spannen immer eine Ebene auf. Im vorliegenden Fall geht es um diejenige Ebene, in der die Mittelpunkte von Sonne, Erde und Mond liegen. Sie enthält auch die durch die Mittelpunkte von Sonne und Erde verlaufende Achse der Schattenkegel. Deren Winkel und alle relevanten Sehwinkel sind in ihr abgebildet (s. Abb.4 u. Abb.5). f1 und f2 werden mit bekannten, während der Finsternis als konstant angenommenen Größen ausgedrückt, mit:
(10) f2 = πM + πS - ρS ( gemäß Abb.5: Δ V2M'E <> f2 = πM - v2 Δ M'ES' <> v2 = ρS - πS ) Die Sehwinkel der von der Erde verursachten zwei Schattenkreise können ebenfalls zwei Besselschen Elementen, nämlich den Durchmessern der bei einer Sonnenfinsternis vom Mond verursachten zwei Schattenkreise gegenübergestellt werden. Die Verwandtschaft ist auch hierbei gering: 1. Es handelt sich einerseits um Sehwinkel, andererseits um Durchmesser. 2. Die Schatten befinden sich einerseits auf einer den Mond enthaltenden Sphäre, andererseits auf der die Erde schneidenden Besselschen Fundamentalebene.
3.4 Sehwinkel des Mondes bei Kontakten ↑Die Bewegung des Mondes relativ zu den Erdschatten ergibt sich aus den zu verschiedenen Zeitpunkten aus seinen Ephemeriden errechneten Sehwinkeln. Von besonderem Interesse sind die Zeitpunkte der Kontakte mit den Schatten. Dafür werden die Sehwinkel vorgegeben und die entsprechenden Zeitpunkte ermittelt. Ein Kontakt ist die Berührung eines Schattenkreises durch den Mondkreis (s. Abb.6). Es interessieren:
4. Rechenbeispiel ↑Eine wichtige Vorarbeit für die Detailberechnung einer bevorstehenden Finsternis ist die Beschaffung der äquatorialen Winkelkoordinaten von Sonne und Mond (Ephemeriden) für mehrere eng benachbarte Zeitpunkte (z.B. alle 10 Minuten). Die Berechnung der Ephemeriden aus den Bewegungsgleichungen der Himmelskörper ist grundsätzlich möglich, in der Regel aber durch den Laien wegen der Forderung nach hoher Genauigkeit praktisch nicht möglich. Werte hoher Genauigkeit werden von einschlägigen Diensten angeboten [6]. Zur Erleichterung der Rechnungen, die eher als Fleißarbeiten anzusehen sind, wird man sich ein Computer-Rechenprogramm anfertigen (oder eins im Internet suchen). Die folgende Wiederholung einer vorgefundenen [7], von Hand gemachten Berechnung der Situation einer vergangenen Mondfinsternis zu einem einzigen Zeitpunkt ist lediglich als Abrundung meiner "Fußwanderung" durch das Thema "Mondfinsternis und Besselsche Elemente ? " gedacht.
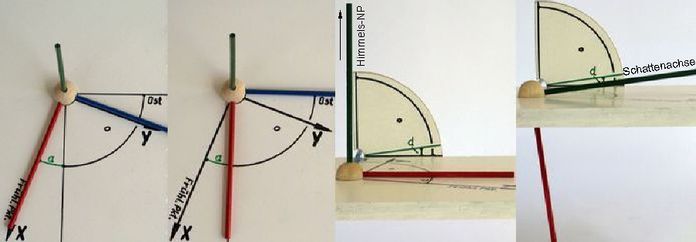
Partielle Mondfinsternis vom 13. März 1975, 21h UT: 5. Anhang: Herleitung der Gleichungen (5) und (6) ↑5.1 Im Zielsystem zeigt die x-Achse nach Osten ↑ nach oben ↑ zurückDie Richtung zum Mond ist mit den Ephemeriden αM und δM im äquatorialen Koordinatensystem angegeben. Gesucht ist diese Richtung relativ zur Polachse des Zielsystems: Sehwinkel σ . Zwischenschritt ist die Ermittlung der kartesischen Koordinaten in beiden Systemen. Die im äquatorialen System ermittelten Koordinaten werden mit Hilfe der Drehmatrix, die die Verdrehung zwischen beiden Systemen beschreibt, in die im Zielsystem gesuchten umgerechnet. Aus letzteren werden die sphärischen Koordinaten im Zielsystem bestimmt (Anmerkung 3).
Die Drehmatrix beschreibt eine Drehung in zwei Schritten (Abb.8, Anmerkung 4):
Der Winkel ζ der ersten Drehung ist (a + π/2) mit (a = αS - π),
Der Winkel χ der zweiten Drehung ist (π/2 - d) mit d = -δS,
und nach dem Multiplizieren:
5.2 Im Zielsystem zeigt die y-Achse nach Osten ↑ nach oben ↑ zurück
Die Drehungen des Koordinatensystems in zwei Schritten sind (Abb.9):
Der Winkel ζ der ersten Drehung ist a mit (a = αS ± π),
Der Winkel ψ der zweiten Drehung ist wie χ in 5.1 (π/2 - d) mit d = -δS,
und nach dem Multiplizieren:
6. Literatur ↑
[1] Friedrich Wilhelm Bessel: "Astronomische Untersuchungen", Zweiter Band, Königsberg, 1842, S. 95: 7. Anmerkungen ↑
Anmerkung 1 ↑ zurück
Anmerkung 2 ↑ zurück
Anmerkung 3 ↑ zurück
Anmerkung 4 ↑ zurück
Anmerkung 5 ↑ zurück
Siegfried Wetzel, CH 3400 Burgdorf, Februar 2013 (März 13, Juli 15, Mai 18)
|
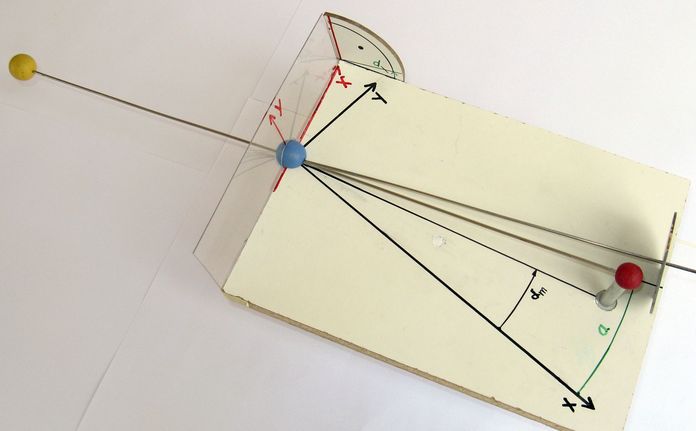Abb.1 Sonne (gelb), Erde (blau), Mond (rot) und Schattenachse (Erdschatten als grau-schwarze Scheibe, rechts)
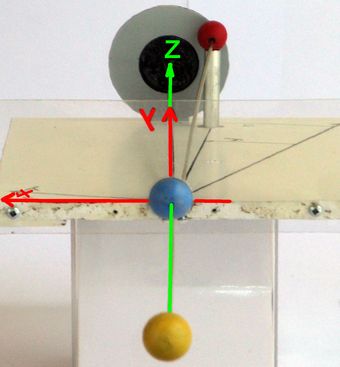Abb.2 >>
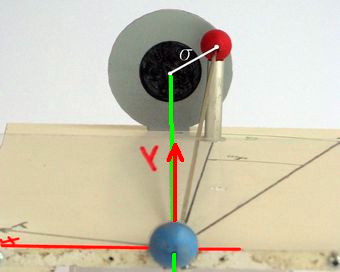Gemäß meinem Anliegen, zu zeigen, dass zwischen den für Sonnenfinsternis-Betrachtungen vorteilhaften Besselschen Elementen und der Untersuchung von Mondfinsternissen zwar rechnerische Ähnlichkeiten, aber kein zwingender Zusammenhang besteht, werde ich die Gleichungen (5) und (6) nicht durch Abwandeln der übernommenen Gleichungen (3) und (4) gewinnen, sondern sie im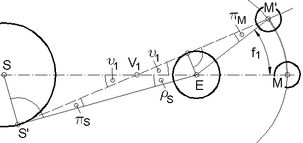 
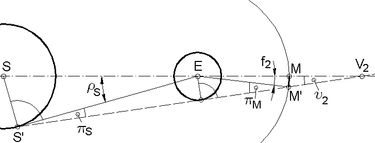Abb.4: Bestimmung des Sehwinkels f1 des Halb- Abb.5: ... des Sehwinkels f2 des Kern-Schattenradius 
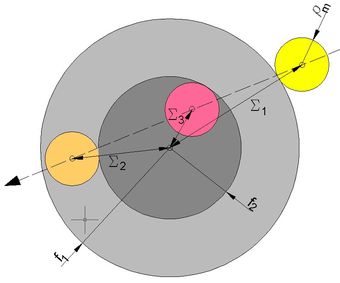Abb.6 >>
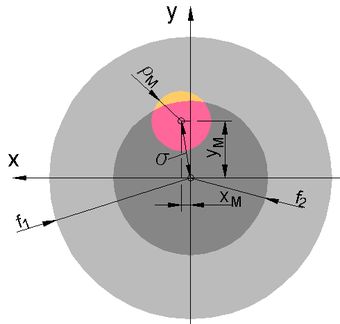Rechenergebnisse: Maßstäbliche Darstellung → Abb.7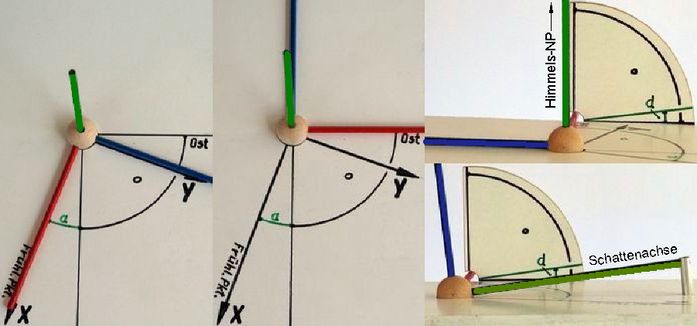
,
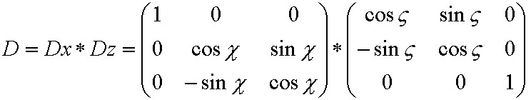
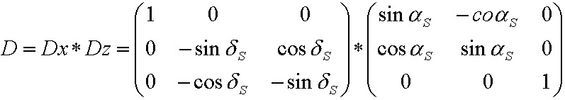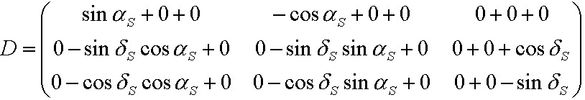
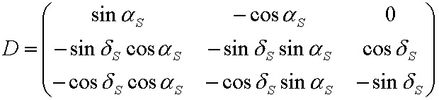
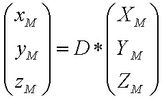Die Drehmatrix auf die äquatorialen Koordinaten XM, YM und ZM des Einheits-Ortsvektors zum Mond angewendet ergibt die Koordinaten xM, yM und zM des Einheits-Ortsvektors zum Mond im Bezugskoordinatensystem: >>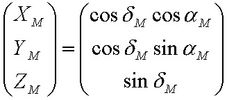
,
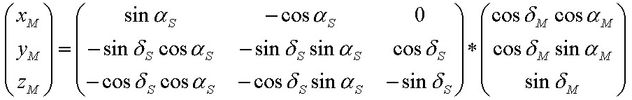
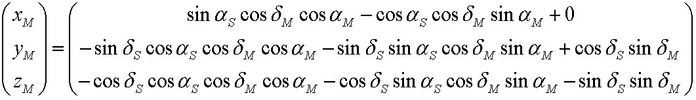
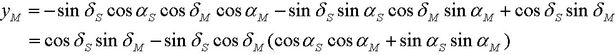
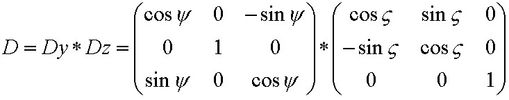
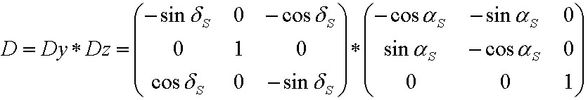