
<< Home
<< andere Astronomie-Beiträge
↓↓ Ende
Sonnenfinsternis und Besselsche Elemente
Inhalt
1. Einleitung
2. Astronomische Elemente in astronomischen Jahrbüchern
3. Erklärung der Besselschen Elemente am Beispiel des Mondschattens
3.1 Fundamentales Koordinatensystem und Fundamentalebene
3.2 Besselsche Elemente
4. Ermittlung der Besselschen Elemente
5. Berechnung der Besselschen Elemente
5.1 Elemente Deklination und Stundenwinkel der Schattenachse
5.2 Elemente x- und y-Koordinate der Schattenachse auf der Fundamentalebene
5.3 Elemente Kegelwinkel des Halb- und des Kernschattens
5.4 Elemente Radius des Halb- und des Kernschattens auf der Fundamentalebene
6. Beispiel-Berechnung Besselscher Elemente
7. Literatur
8. Anmerkungen
Die Besselschen Elemente sind geometrische Größen, die Friedrich Wilhelm Bessel in der ersten Hälfte des 19. Jahrhunderts für die Beschreibung des eine Sonnenfinsternis verursachenden Mondschattens eingeführt hat. Mit ihnen werden in einem zweiten Schritt der Rand des Mondschattens auf der Erdoberfläche und wie die Bedeckung der Sonne durch den Mond an individuellen Beobachtungsorten aussieht, berechnet. Ein- und derselbe Mondschatten ist zu einem gegebenen Zeitpunkt für ganz unterschiedliche Beobachtungsergebnisse an den unterschiedlichen Beobachtungsorten verantwortlich. Bessels Verdienst war, mit der Beschreibung des Mondschattens eine für alle Beobachtungsorte nutzbare Berechnungsgrundlage für Vorhersagen geschaffen zu haben. Vorher war es üblich, dass jede ortsabhängige Berechnung diese vorbereitende Arbeit in irgend einer Art und Weise einschloss, also grundsätzlich vielfach vorgenommen wurde.
Welche Bewandtnis hat es mit dem Ausdruck Elemente?
Hilfreich ist der Hinweis, dass wir uns hier in der Wissenschaft Astronomie befinden. Sie gehört zwar zur Physik, man merkt ihr aber immer noch ihre besondere Vergangenheit in der Nähe zur Astrologie an. In letzterer muß man sich zum Beispiel daran gewöhnen, dass in der Physik streng definierte Begriffe anders und ziemlich unscharf verwendet werden. Genannt sei der Begriff Energie. Die astronomischen Elemente sind zwar eng gefasst, werden aber nicht als etwas Materielles wie in allen anderen Disziplinen behandelt, nicht wie die chemischen Elemente, die galvanischen Elemente, die Bauelemente (z.B. für Maschinen die Maschinenelemente) oder die kriminellen Elemente. Alle lassen sich anfassen, letztere können auch gefasst werden. Astronomische Elemente sind immaterielle Objekte geometrischer Natur. Es sind nicht einmal geometrische Größen ohne weiteren Zusatz, sondern im Allgemeinen sich zeitlich ändernden Werte dieser Größen, die als die astronomischen Elemente bezeichnet werden. Die bei einer Sonnenfinsternis gebrauchten, als jeweiliger Satz für kurz aufeinanderfolgende Zeitpunkte (z.B. alle 10 Minuten) angegebenen Besselschen Elemente sind:
- Werte für die Ausrichtung eines im Erdmittelpunkt errichteten Bezugs-Koordinatensystems, dessen z-Achse der Schattenachse (Verbindungslinie zwischen Sonnen- und Mondmittelpunkt) parallel ist,
- Koordinatenwerte für den Durchstoßpunkt der Schattenachse auf der x/y-Ebene (Besselsche Fundamentalebene),
- Werte für die Radien der Mondschattenkreise auf der Fundamentalebene,
- Werte für Kegelwinkel des Mond-Kern- und Halbschattens.
Diese bei einer Sonnenfinsternis gebrauchten Elemente, ihre Gewinnung und ihre Verwertung zu beschreiben, ist der Inhalt der folgenden Arbeit.
Noch ein Hinweis auf in der Astronomie vorkommende Eigenarten am Beispiel der sogenannten Zeitgleichung:
In der Mathematik verbirgt sich hinter dem Begriff Gleichung eine Gleichheit, im besonderen die Gleichheit zwischen dem, was links beziehungsweise rechts des Gleichheitszeichens = steht. Zeitgleichung benennt aber einen Unterschied, nämlich den zwischen der sogenannten wahren Sonnenzeit (die von der Sonne repräsentierte, nicht gleichmäßig vergehende Zeit) und der sogenannten mittleren Sonnenzeit (die von einer fiktiven Sonne repräsentierte, gleichmäßig vergehende "bürgerliche" Zeit). Es steht auch nicht eine Rechengröße sondern ihr Wert im Vordergrund. Einer Tabelle wird ein Wert in Minuten als die momentane Zeitgleichung entnommen und zur mittleren/wahren Sonnenzeit addiert/subtrahhiert, um die jeweils andere Zeit zu ermitteln.
2. Astronomische Elemente in astronomischen Jahrbüchern ↑ Anfang
Die Besselschen Elemente für bevorstehende Sonnenfinsternisse und andere von der Erde aus beobachtbare Bedeckungen zwischen Himmelskörpern werden heute von nationalen astronomischen Gesellschaften berechnet und in Jahrbüchern (zum Beispiel im nordamerikanisch/britischen Astronomical Almanac[1]) veröffentlicht. Dort sind sie eine Ergänzung zu den Ephemeriden (primäre Gruppe astronomischer Elemente), mit denen die voraus bestimmten, zeitlich veränderlichen Positionen der beweglichen Himmelskörper (Sonne, Mond, Planeten u.a.) in allgemeiner Form bekannt gemacht werden. Die Besselschen Elemente sind ihrem besonderen Zweck dienende Umrechnungenen der Ephemeriden (inkl. Abständen von der Erde) und der Durchmesser der beiden beteiligten Himmelskörper. Sie werden nur für die Dauer der jeweiligen Bedeckung, dafür aber in wesentlich kürzeren Zeitabständen (z.B. alle 10 Minuten einmal; Ephemeriden z.B. nur von Tag zu Tag einmal) erstellt. Die Ephemeriden selbst beruhen auf den sogenannten Bahnelementen [2] und deren zahlreichen aktuellen Korrekturen. Die Bahnen der Himmelskörper sind nämlich in Form und Lage nicht stabil. Sie sind keine exakten Ellipsen (sogenannte Kepplersche Bahnen), und ihre Lagen im Weltraum ändern sich mit der Zeit. Beides trifft in relativ starkem Maße auf die Mondbahn zu. Die Beachtung ihrer kleinen Veränderungen ist entscheidend für eine gute Sonnenfinsternis-Prognose. Bahnelemente sind grundsätzlich keine zeitliche Folge von Werten für geometrische Größen, sondern die Konstanten in Bewegungsgleichungen. Elemente wie Ephemeriden sind zunächst mit diesen Gleichungen für betimmte Zeitpunkte ermittelte Ortsangaben für Himmelskörper, die danach mit mehreren Korrekturfaktoren und Korrekturgleichungen so verändert werden, dass sie der kommenden Realität besser entsprechen.
Zur Berechnung der Besselschen Elemente gibt es heute eine Vielzahl von der Allgemeinheit benutzbarer elektronischer Rechenprogramme, vor allem für die für Sonnenfinsternisse gebrauchten Elemente. Auch für die Anwendung der Besselschen Elemente zur Ermittlung der örtlichen Verhältnisse auf der Erdoberfläche bei einer Sonnenfinsternis (zum Beispiel die Bedeckungsdauer an einem bestimmten Ort oder der Pfad, auf dem sich der Kernschatten über die Erdoberfläche bewegt), werden interessierten Laien Rechenprogramme zur Verfügung gestellt. Letztlich ist es am bequemsten, die zuverlässig und "flächendeckend" berechneten und veröffentlichen Finsternis-Voraussagen der NASA zu benutzen [3] (und sich die Mühe für das Verständnis der Besselschen Elemente und ihrer Anwendung zu ersparen).
3. Erklärung der Besselschen Elemente am Beispiel des Mondschattens ↑ Anfang
Auf der sonnenabgewandten Seite des Mondes entstehen Schatten, ein Kernschatten und ein diesen umgebender Halbschatten. Wenn diese Schatten auf die Erde fallen, sind sie die Akteure einer Sonnenfinsternis. Um letztere beschreiben und ihren Verlauf vorhersagen zu können, ist von der Geometrie und der Lage der Schatten relativ zur Erde auszugehen.
Ihre Form (Kegelwinkel, f1 und f2, s. Abb.3) und gegenseitige Lage (gekennzeichnet durch die Kegelspitzen V1 und V2, Gerade zwischen beiden = Schattenachse, s. Abb.3) ergeben sich schon aus der relativen Lage von Sonne und Mond.
Zur Angabe der Schatten relativ zur Erde wählte Bessel ein kartesisches Koordinatensystem (Besselsches Fundamentalsystem) mit Ursprung im Erdmittelpunkt (s. Abb.n 3 und 1). Deren z-Achse ist parallel zur Schattenachse (positive Richtung zur Sonnenseite der Erdoberfläche), wodurch deren kleinster Abstand zum Erdmittelpunkt in der x/y-Ebene des Systems (Besselsche Fundamentalebene) erscheint.
- Die Werte der äquatorialen Winkel-Koordinaten der positiven z-Achse sind 2 Besselsche Elemente.
- Die Werte der x- und y- Koordinate des Durchstoßpunktes der Schattenachse sind 2 weitere Besselsche Elemente.
- Die Schnitte der Schattenkegel mit der Fundamentalebene sind kreisförmig. Die Werte der Radien der Schnittkreise sind wiederum 2 Besselsche Elemente. Sie ersetzen die Angabe der Lagen der beiden Kegelspitzen.
- Die Werte der als Konstanten behandelten halben Kegelwinkel der Schatten (s.o.) werden als Besselsche Elemente, deren Gesdamtzahl 8 hiermit erreicht ist, übernommen.
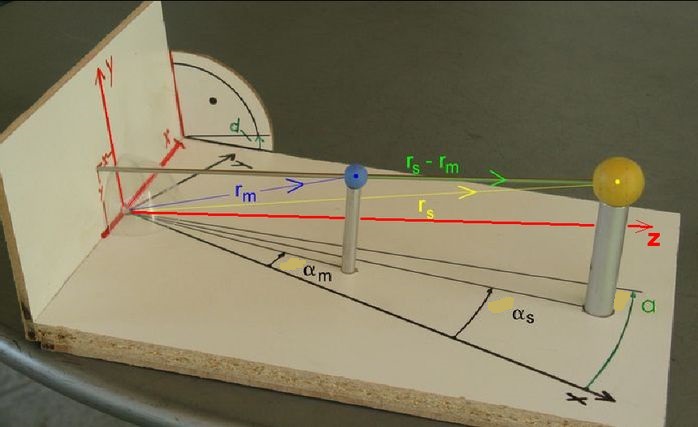
Abb.1 Sonne (gelb), Mond (blau) und Erde (durchsichtig) in einem Modell
Äquatoriales Kordinatensystem (X/Y-Ebene auf großem Brett, Achsen schwarz)
Rektaszensionswinkel αs u. αm von Sonne u. Mond sind verzeichnet
Deklinationswinkel δs u. δm von Sonne u. Mond als gestützte Höhen (|rs|sinδs u. |rm|sinδm)
indirekt erkennbar
Besselsches Fundamentalsystem (x/y-Ebene = Fundamentalebene auf kleinem Brett, Achsen rot).
3.1 Fundamentales Koordinatensystem und Fundamentalebene ↑ Anfang
Das fundamentale Koordinatensystem enthält den Erdmittelpunkt und ist zu jeder Zeit so orientiert, dass seine z-Achse parallel zur Schattenachse ist (s. Abb.1). Die positive Seite der z-Achse zeigt zur besonnten Seite der Erdoberfläche. Die x/y-Ebene ist die Fundamentalebene. Die Schnittgerade der Fundamentalebene mit der Äquatorebene ist die x-Achse, deren positive Richtung von der besonnten Seite der Erdoberfläche aus gesehen Osten ist. Das fundamentale ist wie das äquatoriale ein rechtshändiges Koordinatensystem, wodurch sich die positive Richtung der y-Achse ergibt (s. Abb.1).
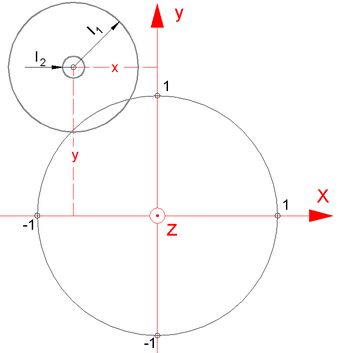
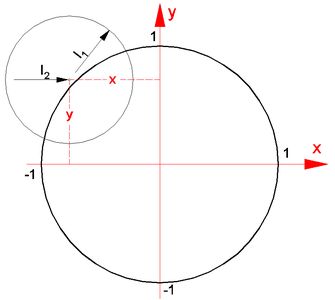
<< Abb.2 Fundamentalebene (x/y-Ebene, Achsen rot):
Besselsche Elemente
l1, l2, x und y
(normiert auf Radius der Erde = 1)
3.2 Besselsche Elemente ↑ Anfang
Besselsche Elemente 1 und 2: (s. Abb.1)
Die Orientierung des fundamentalen Koordinatensystems wird durch die Koordinaten Deklination d und Stundenwinkel μ im ortsfesten äquatorialen Koordinatensystem für die Richtung der positiven z-Achse angegeben. Der ortsfeste Bezug ist der Nullmeridian (durch Greenwich).
Üblicherweise wird zuerst die Rektaszension a im rotierenden äquatorialen Koordinatensystem und daraus anschließend der Greenwich-Stundenwinkel μ mit der Formel
μ = Θ - a
errechnet. Darin ist Θ die Sternzeit von Greenwich.
Besselsche Elemente 3 und 4: (s. Abb.2)
Bei einer Sonnenfinsternis entstehen in der Fundamentalebene zwei Schatten-Randkreise (von Halb- und Kernschatten des Mondes) mit den Radien l1 und l2.
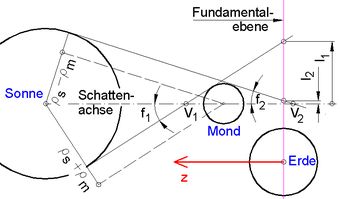
<< Abb.3 Ebene mit Sonne, Mond und Erde:
Radien ρs und ρm von Sonne und Mond führen
zu
Kegelwinkeln f1 und f2 und
Radien
der Schattenkreise l1 und l2
Besselsche Elemente 5 und 6: (s. Abb.n 1 und 2)
Die Schatten-Randkreise haben ein gemeinsames Zentrum, dessen x- und y-Koordinatenwerte angegeben werden.
Besselsche Elemente 7 und 8: (s. Abb.3)
Neben den bisher aufgezählten sechs Größen, die sich alle im Verlauf der Bedeckung ändern, gibt es bei einer Sonnenfinsternis wegen der Kegelform der Mondschatten noch zwei weitere, letztlich die Schattenränder auf der Erdoberfläche bestimmende Größen, die sich aber während der Finsternis wenig ändern und als konstant betrachtet werden können: der halbe Kegelwinkel f1 des Halb- und f2 des Kernschattens. Sie vervollständigen die Besselschen Elemente für eine Sonnenfinsternis auf die Gesamtzahl Acht (Anmerkung 1).
4. Ermittlung der Besselschen Elemente ↑ Anfang
Die acht für eine Sonnenfinsternis gebrauchten Besselschen Elemente werden aus acht anderen Bestimmungsstücken ermittelt. Diese sind:
- die Richtungskoordinaten α und δ von Sonne und Mond (gehören zu den Ephemeriden) = vier Bestimmungssücke (je zwei für einen bestimmten Zeitpunkt im rotierenden Äquatorialen Koordinatensystem angegebene Richtungswinkel),
- die Entfernungen r der Sonne und des Mondes zu einem bestimmten Zeitpunkt vom Erdmittelpunkt (gehören zu den Ephemeriden, dort meistens als Horizontalparallaxen angegeben) = je ein Bestimmungsstück,
- Die konstanten Größen (Radius ρ) der Sonne und des Mondes = je ein Bestimmungsstück.
Für die Angabe der Richtung (Besselsche Elemente 1 und 2: d u. a) und der Lage
(Besselsche Elemente 5 und 6: x u. y) der Schattenachse werden die Richtungskoordinaten und die Entfernungen von Sonne und Mond benötigt. Aus ihnen gemeinsam ergeben sich die äquatorialen Ortsvektoren rs und rm von Sonne und Mond, aus denen schließlich die Schattenachse und die Richtung der fundamentalen z-Achse folgen (s. Abb.4).
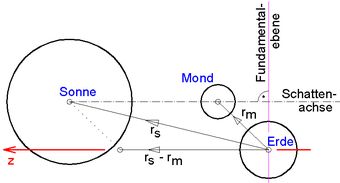
<< Abb.4 Ebene mit Sonne, Mond und Erde:
Ortsvektoren rs und rm → Schattenachse,
Differenzvektor (rs - rm) → fundamentale
z-Achse
Wegen der im Vergleich zu Sternen geringen Entfernung der Sonne und des Mondes von der Erde und ihrer daraus folgenden deutlich feststellbaren scheinbaren Größe wirft der Mond kegelförmige Schatten (Kern- und Halbschatten). Die Besselschen Elemente 3 u. 4 und 7 u. 8, die die Radien l1 u. l2 der Schattenkreise und die Winkel f1 u. f2 der Schattenkegel angeben, benötigen zu ihrer Bestimmung zusätzlich die Radien ρ1 u. ρ2 von Sonne und Mond
(siehe Abb.3).
Die Abstände von Sonne und Mond von der Erde sind wesentlich zu groß beziehungsweise ihre Durchmesser wesentlich zu klein, um die Besselschen Elemente graphisch ermitteln zu können. Die Abbildungen zeigen die Zusammenhänge grundsätzlich, aber in allen sind die Verhältnisse übertrieben unmassstäblich dargestellt. Die Ermittlung der Besselschen Elemente lässt sich mit erforderlicher Genauigkeit nur rechnerisch durchführen.
5. Berechnung der Besselschen Elemente ↑ Anfang
Literatur: [5] und [6]
5.1 Elemente Deklination und Stundenwinkel (beziehungsweise Rektaszension) der Schattenachse ↑ Anfang
Parallel zur Schattenachse liegt der Differenzvektor rs - rm (Abb.4), der als Richtungsvektor für die z-Achse des funamentalen Systems gebraucht werden kann. Als Einheitsvektor - also auf seine Länge |rs - rm| bezogen - ist er identisch mit dem Einheitsvektor k der fundamentalen z-Achse:
(1) (rs - rm) / |rs - rm| = k .
Im äquatorialen Koordinatensystem ist k ein allgemeiner Einheitsvektor, dessen Richtungswinkel (sphärische Koordinaten) die gesuchten Winkel a und d sind. Die bekannte Beziehung zwischen sphärischen und kartesischen Koordinaten lautet:
(2) k = { cos d · cos a cos d · sin a sin d } (Anmerkung 2),
Analog und mit absoluter statt Einheitslänge gelten für die Ortsvektoren zur Sonne und zum Mond mit den vorgegebenen sphärischen Koordinaten α und δ:
(3) rs = rs { cosδscosαs cosδssinαs sinδs } ,
(4) rm = rm { cosδmcosαm cosδmsinαm sinδm } .
Die Gleichungen (2) bis (4) werden in Gleichung (1) eingesetzt, (2) auf die rechte, (3) und (4) in den Zähler der linken Seite. Die drei Gleichungen für die kartesischen Komponenten X, Y und Z des Einheitsvektors k sind getrennt auszuwerten. Sie lauten:
X: (5) (rscosδscos αs - rmcosδmcos αm) / |rs - rm| = cos d · cos a ,
Y: (6) (rscos δssin αs - rmcosδmsin αm) / |rs - rm| = cos d · sin a ,
Z: (7) (rssinδs - rmsinδm) / |rs - rm| = sin d .
Es sind drei Geichungen für die Berechnung der beiden Unbekannten d und a (beziehungsweise μ , siehe 3.2) entstanden.
Zur Auswertung wird noch die im Nenner der linken Seiten dieser Gleichungen stehende Länge des Differenzvektors benötigt. Sie ist mit den Zählern der linken Seiten als Raumdiagonale wie folgt festgelegt:
|rs - rm| =
= ((rscosδscosαs - rmcos δmcosαm)2 + (rscosδssinαs - rmcosδmsinαm)2 + (rssinδs - rmsinδm)2) ½
Die Entfernungen rs und rm sind in den Ephemeridentabellen enthalten, entweder absolut in Kilometern oder relativ zur mittleren Entfernung zwischen Sonne und Erde (Astronomische Einheit AE = 149'597'871 km) oder als Winkel der Horizontalparallaxe (bezogen auf 6.378 km als Äquatorradius der Erde).
5.2 Elemente x- und y-Koordinate der Schattenachse ↑ Anfang
Die Besselschen Elemente x und y sind die Koordinaten von Sonne und Mond im fundamentalen System. Sie können mit dem bekannten standardisierten
Verfahren Verdrehung eines Koordinatensystems in ein anderes (bzw. die Ermmittlung der Koordinaten im anderen Koordinatensystems) mit Drehmatrizen ( Stichwort: Eulerwinkel ) aus ihren äuatorialen Koordinaten berechnet werden. Im vorliegenden Fall wird dieses Vorgehen zwar erwähnt, sein Gebrauch aber nicht beschrieben ([6]). Die Ergebnisse folgen ohne detaillierte Herleitung ([5] und [6]). Ich füge die fehlenden Herleitungen (Herleitung und Gebrauch der Gesamt-Drehmatrix D) hinzu.
Die Drehwinkel sind Funktionen von a und d, deren Berechnung oben angegeben ist. Sie gehen in die Drehmatrix D ein, die die Verdrehung in zwei Schritten beschreibt (Abb.5, Anmerkung 3).
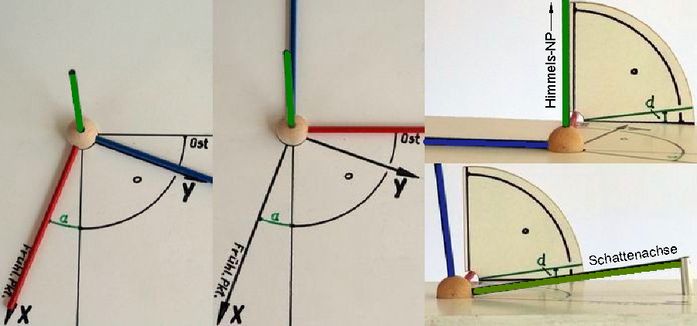
Abb.5 Drehung zwischen äquatorialem (X,Y,Z) und fundamentalem Koordinatensystem (x,y,z) mit x-Achse nach Ost
Die erste Drehung wird um die äquatoriale Z-Achse vorgenommen. Drehwinkel ist a+π/2 (X- zu x-Achse). Die zweite Drehung geschieht um die neue x-Achse mit dem Winkel π/2-d. Die neue z-Achse ist nun zur Schattenachse parallel, und die neuen Achsen x und y spannen die Fundamentalebene auf.
Der erste Drehwinkel ist der um π/2 vergrößerte Winkel a, da nicht die fundamentale x-Achse sondern die z-Achse per Definition zur Schattenachse parallel ist (s. Abb.1). Die zweite Drehung mit dem zu d komplementären Winkel ergibt sich aus der für das Fundamentalsystem definierten Rechtshändigkeit.
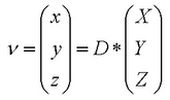
Die Koordinaten (x,y,z) eines Vektors v sind im gedrehten System (Fundamental-) das Produkt der Koordinaten (X,Y,Z) im Ausgangssystem (Äquatorial-) mit der Drehmatrix D (Anmerkung 4): >>
Die Drehmatrix ist das Produkt aus den Matrizen der Einzeldrehungen, dabei steht die Matrix der ersten Drehung hinten (Rechenregel: "von rechts nach links multiplizieren").
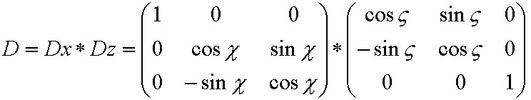
Der Winkel ζ der ersten Drehung ist (a + π/2). Kürzere, gleichwertige Schreibweisen der trigonometrischen Funktionen der Klammerausdrücke sind:
cos (a+π/2) => - sin a und sin (a+π/2) => cos a .
Der Winkel χ der zweiten Drehung ist (π/2 - d). Kürzere, gleichwertige Schreibweisen der trigonometrischen Funktionen der Klammerausdrücke sind:
cos (π/2-d) => sin d und sin (π/2-d) => cos d .
Die verkürzt geschriebenen Winkelfunktionen in die Teilmatrizen eingesetzt und die Multiplikation ausgeführt:
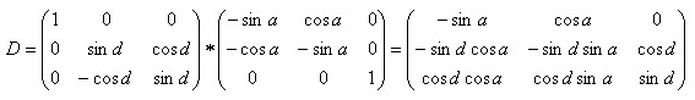
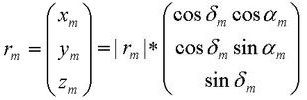
Die gesuchten fundamentalen Koordinaten x und y der Schattenachse sind auch die der äquatorialen Ortsvektoren sowohl zur Sonne als auch zum Mond. Im Folgenden werden die des Mondvektors rm benutzt und
Gleichung (4) in Spaltenvektoren geschrieben: >>
Die Anwendung der Drehmatrix D auf die äquatorialen Mondkoordinaten ergeben die fundamentalen Mondkoordinaten xm, ym und zm (Anmerkung 5):
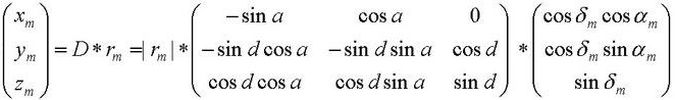
Jede der drei Matrix-Zeilen auf jeden der drei Koordinatenwerte des Spaltenvektors angewendet liefert die Ergebnisse:
(8) x = |rm| · cos δm · sin (αm - a) ,
(9) y = |rm| · (sin δm · cos d - cos δm · sin d · cos (αm - a)) , (Anmerkung 6)
(10) zm = |rm| · (sin δm · sin d + cos δm · cos d · cos (αm - a)) .
xm und ym sind zu x und y verallgemeinert. zm wird für die Berechnung der Schattenradien (Abschnitt 5.4) benötigt.
Die momentane Entfernung |rm| von der Erde zum Mond ist in den Ephemeriden-Tabellen oft indirekt als äquatoriale horizontale Mondparallaxe πm zu finden. Damit und mit dem Durchmesser der Erde RE ist sie errechenbar:
|rm| = RE / sin πm .
Da die Koordinaten x und y der Schattenachse auf den Erdradius am Äquator bezogene Besselsche Elemente sind
(s. Abb.2), ist nur der Kehrwert des Sinus der Parallaxe auszurechnen:
|rm| / RE = 1 / sin πm .
5.3 Elemente Kegelwinkel des Halb- und des Kernschattens ↑ Anfang
Die Besselchen Elemente f1 und f2 sind die Winkel zwischen der Schattenachse und den Tangenten an Sonne und Mond, die die Kegelmäntel des Halb- und Kernschattens bilden (siehe Abb.3). Sie können mittels eines Hilfsdreiecks ermittelt werden. Dabei werden die Tangenten parallel verschoben, so dass sie durch den Mondmittelpunkt gehen. Hypotenuse beider Dreiecke ist die Verbindungslinie des Sonnen- und Mondmittelpunkts, die Gegenkatheten der gesuchten Winkel bilden die auf den parallel verschobenen Tangenten rechtwinklig stehenden Strecken durch den Sonnenmittelpunkt. In diesen rechtwinkligen Dreiecken ist jeweils die Länge zweier Seiten bekannt, zum einen die Entfernung zwischen Sonne und Mond, zum anderen die Länge der Gegenkathete, die beim Halbschatten der Summe aus Sonnen- und Mondradius entspricht, beim Kernschatten der Differenz dieser beiden Größen. Somit gilt:
(11) sin f1 = (ρs + ρm) / (|rs - rm| ,
(12) sin f2 = (ρs - ρm) / (|rs - rm| .
Die Radien ρs und ρm sind konstante Größen:
ρs + ρm = 0,004664018 AE ,
ρs - ρm = 0,004640792 AE .
Die Ermittlung der prinzipiell variablen Entfernung |rs - rm| zwischen Sonne und Mond ist schon im Abschnitt 5.1 beschrieben. Es kann aber ein Mittelwert verwendet werden, der zu während der gesamten Finsternisdauer nicht veränderlichen Kegelwinkeln führt.
5.4 Elemente Radius des Halb- und des Kernschattens auf der Fundamentalebene ↑ Anfang
Um die letzten beiden noch fehlenden Besselschen Elemente l1 und l2 zu errechnen - die Radien von Halb- und Kernschatten in der Fundamentalebene - wird der Abstand der Schnittpunkte der Tangenten mit der Schattenachse von der Fundamentalebene benötigt (s. Abb.3). Für den Halbschatten liegt dieser mit V1 bezeichnete Punkt auf der Schattenachse zwischen Sonne und Mond und stellt die Spitze des Halbschattenkegels dar. Der Schnittpunkt V2 liegt ebenfalls auf der Schattenachse und ist die Spitze – also der Endpunkt – des Kernschattens. Dabei gilt:
(13) zV1 = zm + (ρm / sin f1) ,
(14) zV2 = zm - (ρm / sin f2) .
Mittels dieser Abstände lassen sich die Radien der Schattenkegel in der Fundamentalebene wie folgt ermitteln:
(15) l1 = zV1 · tan f1 ,
(16) l2 = zV2 · tan f2 ,
Wenn die Kegelspitze des Kernschattens vom Mond aus gesehen hinter die Fundamentalebene fällt, also eine totale Sonnenfinsternis vorliegt, ist deren Koordinate zV2 negativ, im anderen Fall positiv (ringförmige Sonnenfinsternis). Dementsprechend wird der Kernschattenradius l2 bei einer totalen Finsternis mit negativem Vorzeichen gekennzeichnet, bei ringförmiger Finsternis hingegen mit positivem. Die Größen zV1 und l1 sind immer positiv.
6. Beispiel-Berechnung Besselscher Elemente ↑ Anfang
Eine wichtige Vorarbeit für die Detailberechnung einer bevorstehenden Finsternis ist die Beschaffung der Koordinatenwerte von Sonne und Mond (Ephemeriden) für mehrere eng benachbarte Zeitpunkte (z.B. alle 10 Minuten). Die Berechnung der Ephemeriden aus den Bewegungsgleichungen der Himmelskörper ist grundsätzlich möglich, in der Regel aber durch den Laien wegen der Forderung nach hoher Genauigkeit praktisch nicht erfolgreich. Werte hoher Genauigkeit werden von einschlägigen Diensten angeboten [6]. Zur Erleichterung der Rechnungen, die eher als Fleißarbeiten anzusehen sind, wird man sich ein Computer-Rechenprogramm anfertigen (oder eins im Internet suchen). Die folgende Wiederholung einer vorgefundenen [7], von Hand gemachten Berechnung Besselscher Elemente für einen einzigen Zeitpunkt der totalen Sonnenfinsternis vom 26. Februar 1979 ist lediglich als Abrundung meiner "Fußwanderung" durch das Thema "Sonnenfinsternis und Besselsche Elemente" gedacht. Für die totale Sonnenfinsternis vom 15. Februar 1961 ist ebenfalls eine solche Einzelberechnung dokumentiert [8].
Totale Sonnenfinsternis vom 26. Februar 1979, 16h UT:
Ephemeriden:
αM = 22h 33m 28,79 s = 338,36997° δM = - 8° 02' 42,98'' = - 8,04527° rM = 0,00242 AE
πM = 1°01'09,99'' = 1,01944° (1 / sin πM = rM/RE)
αS = 22h 36m 36,79 s = 339,15329° δS = - 8° 46' 15,20'' = - 8,77089° rS = 0,99022 AE
 Rechenergebnisse: maßstäbliche Darstellung in Abb.6 >>
Rechenergebnisse: maßstäbliche Darstellung in Abb.6 >>
Gl. (7): d = - 8,77265°
Gl. (5): a = 339,15520°
Gl. (8): xM = - 0,76269
Gl. (9): yM = 0,71273
Gl. (11): f1 = 0,27055°
Gl. (12): f2 = 0,26917°
Gl. (15): l1 = 0,53782
Gl. (16): l2 = - 0,00826
Bemerkungen:
1. Die übernommenen Vorgabewerte (Ephemeriden) habe ich auf ein bis zwei Nachskomastellen weniger gerundet mit dem Vorteil, dass sich die von mir gerechneten und ebenfalls mit weniger Nachkommastellen geschriebenen Ergebnisse nicht mehr von den Ergebnissen in [7] unterscheiden.
2. Die Mond-Koordinaten (Ephemeriden) gelten für den Mondschwerpunkt, die Mondschattenkreise beziehen sich aber auf den geometrischen Mondschwerpunkt. Die übernommenenen Mond-Werte waren bereits entsprechend korrigiert.
3. AE = Astronomische Einheit (mittlere Enfernung zwischen Erd- und Sonnenmittelpunkt)
4. Die mit den Gleichungen (8) und (9) errechneten Koordinaten x und y wurden auf den Erdradius RE (am Äquator) durch Division mit dem Sinus der Mondparallaxe πM normiert.
5. Die Schattenachse befindet sich zum berechneten Zeitpunkt noch außerhalb der Erde (vergleiche Kontaktzeiten U1 und U2, Anmerkung 6). Der Radius l2 des Mond-Kernschattens ist zu klein, um in Abb.6 erkannt zu werden.
[1] Astronomical Almanac – Data for Astronomy, Spaces Sciences, ... (z.B. für 2013)
[2] H.Peter und M.Styx: Astronomie: alte Geschichten und neue Physik, Vorlesung an der Uni Freiburg, WS 2003/04,
Seite 17 (.PDF-File)
[3] NASA Eclipse Web Site: Solar Eclipse Page
[5] Robin M. Green: Sperical Astronomy, Cambridge University Press, 1985, Seiten 450 - 453, ISBN 0-521-23988-5
[6] P. Kenneth Seidelmann (Hrsg.): Explanatory Supplement of the Astronomical Almanac, University Science Books,
1992, ISBN 0-935702-68-7, S. 435-41
[7] H. Mucke: Die Geometrie astronomischer Finsternisse, Sternfreunde-Seminar, Wiener Planetarium, 1999
[8] Explanatory Supplement of the Astronomical Almanac 1961, 4th impression 1977,
scans der Seiten 211-24 bei dermuehle.blogspot.ch/2012/04: Besselsche Elemente
Anmerkung 1 ↑ zurück
In der Praxis werden oft weitere Größen (Elemente) aufgelistet. Dabei handelt es sich vorwiegend um Faktoren, die zur Interpolation für weitere Wertesätze benötigt werden, wenn das zeitliche Intervall zwischen den angegebenen Wertesätzen relativ groß ist, oder nur ein Wertesatz für einen einzigen Zeitpunkt angegeben wird. Mitunter werden auch zusätzliche Größen angegeben, die zu einem oder mehreren der 8 Grund-Elemente redundant sind.
Anmerkung 2 ↑ zurück
In der gewählten Schreibweise in Matritzen-Form werden die karthesischen Koordinaten als Funktionen der sphärischen Koordinaten zusammengefasst dargestellt (Zeilen-Vektor). Ausgeschrieben lauten die Koordinaten z.B. anstatt Gl.n (3) und (4):
X = r cosδ cosα ,
Y = r cosδ sinα ,
Z = r sinδ .
Anmerkung 3 ↑ zurück
Vom äquatorialen zum fundamentalen System sind es nicht wie im allgemeinen Fall drei Drehungen mit drei Eulerwinkeln. Es finden nur zwei Drehungen statt, weil die fundamentale x-Achse in der äquatorialen XY-Ebene verbleibt.
Anmerkung 4 ↑ zurück
Im Unterschied zu den Gleichungen (2) bis (4) ist v als Spaltenvektor geschrieben.
Anmerkung 5 ↑ zurück
Die Zeilen der Drehmatrix D sind identisch mit den Einheitsvektoren i, j und k des fundmentalen Koordinatensystems (Matritzen-Schreibweise). Man kann die vorgenommene Rechnung auch als drei skalare Mulitiplikationen des Vektors zum Mond mit diesen Einheitsvektoren auffassen oder sie durch diese Multiplikationen ersetzen. Die Einheitsvektoren sind leicht zu formulieren (k bereits gemacht). Durch skalare Multiplikation eines Vektors mit einem Einheitsvektor gewinnt man bekanntlich seinen Anteil in Richtung des Einheitsvektors, im vorliegenden Fall die fundamentalen kartesischen Koordinatenwerte des Mondes (x und y stellvertretend für die Schattenachse).
Anmerkung 6 ↑ zurück
Herleitung von beispielsweise Gl.(9) mit im Haupttext nicht gezeigter Zwischenrechnung unter Anwendung eines Additionstheorems:
y = |rm| (- sin d cos a cosδmcosαm - sin d sin a cosδmsinαm + cos d sinδm)
y = |rm| (cos d sinδm - sin d cosδm(cos a cosαm + sin a sinαm))
y = |rm| (cos d sinδm - sin d cosδmcos( αm - a))
Anmerkung 7 ↑ zurück
UT unterscheidet sich von ET nur um etwa 50 Sekunden.
 Siegfried Wetzel, CH 3400 Burgdorf, August 2012 (Nov.12, Febr.13, März 13, Juni 13, Juli 15, Nov.20)
Siegfried Wetzel, CH 3400 Burgdorf, August 2012 (Nov.12, Febr.13, März 13, Juni 13, Juli 15, Nov.20)
↑↑ Anfang
<< andere Astronomie-Beiträge
<< Home





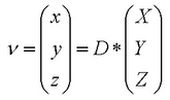
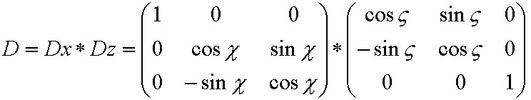
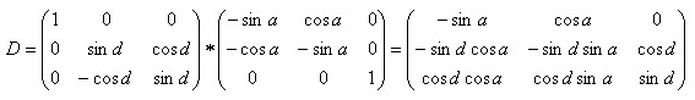
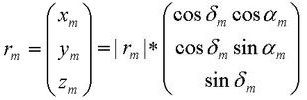
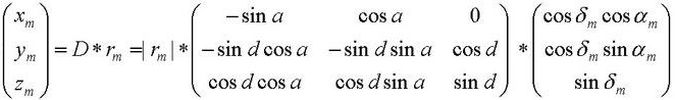
 Rechenergebnisse: maßstäbliche Darstellung in Abb.6 >>
Rechenergebnisse: maßstäbliche Darstellung in Abb.6 >>