<< Home
<< andere Sonnenuhren-Beiträge
 ↓↓ Ende

Die Zeitgleichung für den Mars, elementar behandelt

Vorbemerkung

Inhalt

1. Einleitung

Der berühmte amerikanische Physiker Feynman hielt eine ungewöhnliche Vorlesung für Studienanfänger mit dem auch für die Zeitgleichung bedeutsamen Titel "Die Bewegung der Planeten um die Sonne " [1]. Ungewöhnlich daran war, dass er den darin enthaltenen Ellipsen-Beweis elementar führte. Mit elementar meinte er, dass zum Verständnis wenig Vorwissen, allerdings viel Intelligenz nötig sei. Er leitete den Satz mit vorwiegend geometrischen Überlegungen her, denn Eleganz und Schönheit geometrischer Beweise spreche viele Menschen an. Nachteil sei, dass man anders als bei Verwendung höherer Mathematik mit Geduld viele Schritte machen müsse. Feynman ist Vorbild für die folgende Behandlung der Zeitgleichung. Der von ihm verwendete Begriff elementar wird ab jetzt kursiv geschrieben.

2. Zeitgleichungs-Ursachen

Die wahre Sonnenzeit verläuft auf jedem Planet ungleichförmig. Die dafür geltenden grundsätzlichen Ursachen sind für alle Planeten dieselben. Sie sind für die Erde allgemein bekannt und zur Ermittlung der lediglich quantitativ anderen Verhältnisse z.B. auf dem Mars nutzbar. Mit dem erneut benutztem Begriff elementar soll darauf hingewiesen werden, dass auch die sehr langsamen Veränderungen am Sonnenhimmel des Mars, wie Form und Lage seiner Bahnellipse, seine Jahr-Länge, die Neigung seiner Drehachse u.ä. nicht beachtet werden. Die bekannten Ursachen für das "Falsch-Gehen" der irdischen Sonnenzeit werden auf die astronomischen Verhältnisse auf dem Mars übertragen

Der Mars muss sich auch pro Sonnentag mehr als einmal um sich selbst drehen. Nach einer 360°-Drehhung ist erst ein Sterntag vollendet. Die (von der Sonne überstrahlten) Sterne stehen wieder am selben Ort (Süden, Meridian), die Sonne ist aber wegen der kurzen Bahnfahrt des Mars noch nicht dort angekommen. Deshalb muss er sich zur Vollendung des Sonnentages noch ein Stück weiter drehen (Abb.1). Zwei Ursachen bewirken, dass das täglich unterschiedlich lange dauert.

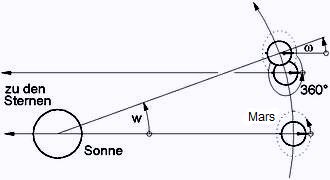
<< Abb.1 Eigendrehung und Bahnfahrt des Mars

Ursache 1: Ellipse bzw. variabler Bahnwinkel
Auf der elliptischen Marsbahn (mit fast sechsfacher Erde-Exzentrizität) ist der Abstand zur Sonne (fast 1,5-facher Erde-Abstand) variabel. In Sonnennähe führt die tägliche (Erde- und Mars-Tag sind fast gleich lang) Bahnfahrt weiter als in Sonnenferne. Die Zusatzdrehung des Mars muss in einer Hälfte des Jahres grösser, in der anderen Hälfte kleiner sein, weshalb in diesen Zeiten der Mars-Tag länger bzw. kürzer als im Durchschnitt ausfällt.

Ursache 2: Ekliptik bzw.variables Verhältnis zwischen Bahnwinkel und zusätzlichem Drehwinkel
Die Richtung der Drehachse des Mars ist im Weltraum auch fix und nicht rechtwinklig zur Bahnebene um die Sonne (fast gleich schief wie die der Erde), weshalb sich das Verhältnis zwischen Bahnwinkel und zusätzlichem Drehwinkel täglich ändert. Zur Zeit der Sonnenwenden ist der Zusatz-Drehwinkel ω grösser als der zu kompensierende Bahnwinkel w_o (maximal, Abb.2, links). Zur Zeit der Tag/Nacht-Gleichen ist er kleiner (minimal, Abb.2, rechts). Die nicht konstante tägliche Bahnfahrt führt also auch nicht 1:1 zur täglichen Zusatzdrehung. In zwei Vierteln des Jahres ist das Verhältnis grösser, in den beiden Vierteln dazwischen kleiner mit den entsprechenden Auswirkungen auf die Länge des Mars-Tages.

Abb.2 Winkelunterschiede zu einer Sonnenwende (links) und zu einer Tag/Nacht-Gleiche (rechts) [2]

3. Schwankung der Tageslänge des Mars

Schwankungen sind relative Angaben zu einer mittleren Grösse. Kleine (<<1) periodische Schwankungen lassen sich in guter Näherung (Näherung #1) mit einer Kreisfunktion (Sinus-, Cosinus-) beschreiben, für die dann nur Amplitude, Periodendauer und Nullpunkt zu bestimmen sind.

Die Wirkungen der beiden Ursachen wären eigentlich miteinander zu multiplizieren. Weil aber beide Schwankungen klein sind, erscheinen sie im Ergebnis in Näherung als Summe (#2, Anmerkung 1). Deshalb ist es möglich, beide Ursachen getrennt zu behandeln und erst am Schluss die Summe aus ihren Wirkungen zu bilden.

3.1 Vorgegebenes

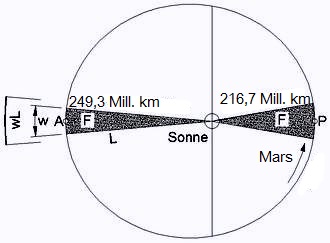<< Abb.3 zweites Keppler'sches Gesetz

Das zweite Keppler'sche Gesetz lautet: Die Verbindungslinie eines Planeten mit der Sonne überstreicht in gleichen Zeitabschnitten gleich grosse Flächen (Abb.3). Der im Folgenden zu betrachtende Zeitabschnitt ist der Sol genannte Mars-Tag. Die Flächen F für diesen Zeitraum sind wesentlich kleiner (spitzer) als abgebildet.

Entfernungen:
(mittlere)   L₀   ( = 228·10⁶ km)
(variable)   L    ( = L₀ ± ΔL = 228·10⁶ km ± 21,3·10⁶ km)
(relative)    l     ( = L/L₀ = 1 ± ΔL/L₀ = 1 ± Δl = 1 ± 0,0934)

Die Schwankung Δl = ± 0,0934 der relativen Entfernung l des Mars von der Sonne ist identisch mit der numerischen Exzentrizität e seiner Bahnellipse. Als geometrische Vorgabe für die Besprechung der Zeitgleichung des Mars ist dieser Bahn-Wert vollständig ausreichend.

Als zeitliche Vorgabe genügt ebenfalls ein relativer Zusammenhang, nämlich die Zahl der Eigendrehungen des Mars während eines seiner Umläufe um die Sonne. Dass die Eigendrehung des Mars (der Sol) zufällig fast gleich lange wie eine Erddrehung (der Tag) dauert, erleichtert lediglich den Vergleich zwischen den Zeitgleichungen dieser beiden Planeten der Sonne: Der Sol ist um den Faktor 1,026 länger als der Erde-Tag. Das Mars-Jahr ist etwa 687 Erde-Tage, aber nur etwa 670 Sol lang.

Der Winkel zwischen der Ekliptik- und der Äquatorebene des Mars beträgt ε = 25,19°
(bei der Erde: 23,44°).

3.2 Ellipse (Ursache 1)

Der etwas genauere Wert für die Länge des Mars-Jahres ist: 669,6 Sol. Der Bahnwinkel während eines Sol beträgt demzufolge nur etwa 0,54° (pro Mars-Jahr eine ganze Bahnrunde =360°). Sein Mittelwert ist:
w₀ = 360°/ 669,6 Sol = 0,5376°/Sol (Bahnwinkel der Erde 0,9856°/Tag).

Die überstrichene Fläche F (Abb.3) ist ein sehr spitzes Kreissegment. Es kann in Näherung (#3) als rechtwinkliges Dreieck mit w·L als kurzer Kathete aufgefasst werden. Die Fläche ist:
F = (wL·L)/2 = wL²/2 (w im Bogenmass, Abb.3).
Umgestellt: w = 2F/L²; analog dazu: w₀ = 2F/L₀² (Mittelwert des täglichen Bahnwinkels).

w auf w₀ bezogen und mit Hilfe der relativen Schwankungsbreite Δl des täglichen Bahnwinkels formuliert:
w/w₀ = L₀²/L² = 1/(1±Δl)² .

Weil Δl<<1 ist, sind zwei weitere Näherungs-Schreibweisen möglich (Anmerkung 2):
#4: (1± Δl)² = (1± 2Δl).
#5: 1/(1± 2Δl) = (1 ∓ 2Δl) ; Kehrwert und Vorzeichenwechsel.

Neue Ausdrucksweise:
w/w₀ = 1 ∓ 2Δl = 1 ∓ 2· 0,0934.

Damit ist die gesuchte relative Schwankungsbreite Δt₁ der Zeit T₁ (Index ₁ für Ursache 1) für den täglichen Zusatz-Dreh des Mars gefunden, denn diese hat dengleichen Wert wie die relative Schwankungsbreite des täglichen Bahn-Winkels.

Die bezogene Zeit hat den Ausdruck:
T₁/T₀ = 1 ± Δt₁ = 1 ± 2Δl = 1 ± 0,1868.
Der absolute Wert der Schwankungsbreite ΔT₁ ist:
ΔT₁ = Δt₁·T₀ = ± 24,07 Sec. .
Die Berechnung der mittleren Zeit lautet: T₀ = 24Std.·w₀ / (w₀ +360°) = 129 Sec. .

      Std., Min. und Sec. sind die Formelzeichen für Zeiteinheiten auf dem Mars, die um den Faktor 1,026 länger als die
      entsprechenden auf der Erde geltenden Einheiten sind.

Der Sol ist in Perihelnähe (P) ca. 24 Sec. länger als im Mittel und in Nähe des Aphel (A) ca. 24 Sec. kürzer. Seine ganzjährige Schwankung aus Ursache 1 lässt sich mit folgender Cosinus-Funktion beschreiben (#1, Anmerkung 3):

(1)  24,07Sec.·cos((d-d₁)·360°/669,6)   (Abb.4).

d ist die Zeit von Winter- bis Winter-Sonnenwende (WWS, auf der Nordhälfte des Mars) über etwa 670 Sol.
Die Kurve hat ihr positives Maximum beim Perihel-Durchgang, der 19 ekliptikale Winkelgrade (= d₁ = 34 Sol) vor der WWS stattfindet.

3.3 Ekliptik (Ursache 2)

Bei Ursache 1 bleibt die Neigung der Mars-Achse um den Winkel ε unberücksichtigt. Jetzt wird die Abbildung von täglich gleichen Bahn-Differenzen in der Ekliptik-Ebene als Winkeldifferenzen in der Äquator-Ebene untersucht. Dem (mittleren, #2) Bahnwinkel w₀ entspricht auf der Marsoberfläche ein täglich gleich großes Bogenstück. Da die Sonnenzeit mit der Eigendrehung des Mars vergeht, ist aber das diesem Bogenstück entsprechende Stück auf dem Äquator zu beachten. Die täglich andere Beziehung zwischen beiden Stücken ist zu finden.

Ermittelt wird der täglich andere Drehwinkel ω. Wegen (#1) genügen Grösst- und Kleinstwert dieses Winkels.

Größtwert, Sonnenwenden (Abb.2, links):
Das w₀ entsprechende Bogenstück auf dem Mars ist Teil eines Grosskreises (Ekliptik). Da es klein ist, darf dieser Kreis durch einen Kleinkreis (Wendekreis) ersetzt werden (#6). w₀ steht dann zu ω_max im gleichen Verhältnis wie die Umfänge von Klein- und Äquatorkreis, das ist
w₀/ω_max = cos ε .
Mit den Werten für w₀ = 0,5376° und ε = 25,19° ist
ω_max = w₀ /cos ε = 0,5941° .

Kleinstwert, Tag/Nacht-Gleichen (Abb.2, rechts):
Das sphärische Doppel-Dreieck aus w₀, ε und ω_min ist klein genug, dass es als ebenes Dreieck angesehen werden darf (#7). In ihm besteht die Beziehung   cos ε = (ω_min/2)/(w₀/2)   bzw.
ω_min = w₀·cos ε = 0,4865° .

Mit sphärischer Trigonometrie lassen sich die Werte exakt bestimmen (Anmerkung 4), man findet aber bei der gewählten Auflösung noch keinen Unterschied.

Die Verarbeitung der beiden Werte führt zu:
mittlerer Wert ω₀ = 0,5403° und
ω = 0,5403° ± 0,0538° .

Die Eigendrehung des Mars erfolgt mit konstanter Geschwindigkeit. Die Zeit T₂ (Index ₂ für Ursache 2) für seinen täglichen Zusatz-Dreh schwankt wie der Drehwinkel ω:
Δt₂ = Δω = 0,0538° .
T₂/T₀ = 1 ± Δt₂ = 1 ± Δω
Mit   T₀ = 129 Sec.    ist       ΔT₂ = Δω·T₀ = ± 6,94 Sec. .

Der Sol ist an den Sonnenwenden ca. 7 Sec. länger als im Mittel, an den Tag/Nacht-Gleichen ca. 7 Sec. kürzer. Seine halbjährige Schwankung aus Ursache 2 lässt sich mit folgender Cosinus-Funktion beschreiben (#1):

(2)   6,94Sec.· cos(2·d·360°/669,6)   (Abb.4)

d ist die Zeit von Winter- bis Winter-Sonnenwende (WWS, auf der Nordhälfte des Mars) über etwa 670 Sol. Die Kurve hat einen ihrer vier Extremwerte bei der WSW.

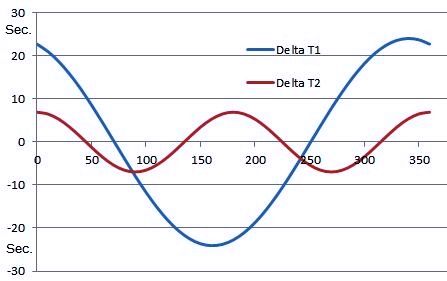
<< Abb.4 Schwankungen der Sol-Länge in Sec.

Abb.4 zeigt die Schwankungen der Sol-Länge
(Funktionen (1) und (2)).
Die Kurven beginnen zur Wintersonnenwende. Die Zeitachse ist über den Winkel eines Kreises (0° bis 360°, entspricht einem Marsjahr von Sol 0 bis Sol 670) skaliert.

4. Vor- und Nachgehen der wahren Sonnenzeit auf dem Mars

4.1 Ellipse (Ursache 1)

In Abb.5 sind die Sol-Verkürzungen aus Ursache 1 zwischen 168. und 502. Sol des Mars-Jahres (in der mittleren Hälfte des Jahres) etwa jeden 9. Tag mit einem Balken gekennzeichnet. Denkt man sich in die Lücken die übrigen Sol-Balken gezeichnet, so ist zwischen der Kurve der Gleichung (1) und der Null-Linie eine gefüllte Fläche entstanden. Sie enthält die Summe aller Verkürzungen in diesem Zeitraum, die der Sonnenuhr von grösstem Nachgehen (-42,74Min.) zu grösstem Vorgehen (+42,74Min.) verhilft. Letzteres zeigt die in Abb.5 auch enthaltene Kurve ZG1 die wegen (#1) eine Sinus-Linie ist. Weil die Steigung hier (Perioden-Mitte) positiv ist, handelt es sich um den negativen Sinus.

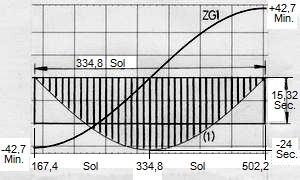
<< Abb.5 Sonnenuhr-"Vorgehen" an zu kurzen Sols

Wie findet man die angegebenen Zahlen-Werte?
Man könnte die Balken-Werte ausrechnen und addieren. Diese Zeitsumme kann aber auch mit Hilfe einer geometrischen Näherung (#8,Anmerkung 5) ermittelt werden. In Abb.6 wird die Kurve M ((1) in Abb.5) von den Kurven K und G eingerahmt (die Amplitude aller drei ist 1; die Skalierung der Zeitachse ist Bogenmaß). Der Halbkreis K enthält die kleinere Fläche (F_K=π/2), und die Halb-Ellipse G als gestreckter Halbkreis enthält die grösseren Fläche (F_G=π²/4, Streckung im Verhältnis π:2).

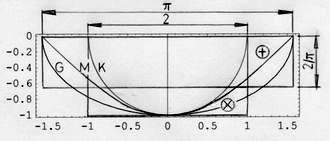
<< Abb.6 geometrische Näherung einer Cosinus-Fläche

Der Mittelwert aus der K- und der G-Fläche kann als die gesuchte Fläche angenommen werden: F_M = (F_K+F_G)/2 = 2,02. Weiter wird mit dem runden Wert 2 gerechnet, der sich auch anbietet bei Näherung der gesuchten Fläche durch das Rechteck 2 mal 1. Die beiden Eck-Flächen Ä und Å scheinen gleich gross zu sein (Anmerkung 6). Das schmale Ersatz-Rechteck hat folglich die "Amplitude" 2/π. In der Fläche von Abb.5 ist die Amplitude nicht 1 sondern 24,07Sec., die beim Rechteck zu 15,32Sec. (24,07Sec.·(2/π)) wird. Die Fläche stellt also 15,32Sec.·334,8 = 5129Sec.. = 2·42,74Min. dar, wie oben angegeben.

Die Amplitude (42,74Min.) und die Phasenlage (negativer Sinus) des elliptischen Teils der Zeitgleichung sind somit gefunden. Die Teilgleichung lautet:

(1a)   ZG1 = - 42,74Min.·sin((d+34)·360/669,6).

d ist die Zeit von 0 bis 670 Sol.

4.2 Ekliptik (Ursache 2)

Zum Vor -und Nachgehen der Sonnenuhr infolge Ursache 2 kommt man mit Überlegungen, die analog zu obigen sind. Die Cosinus-Kurve (2) mit Amplitude 6,94Sec. und der Periode von 334.8 Sol führt zur negativen Sinus-Kurve, der zweiten Teilgleichung:

(2a)   ZG2 = - 6,16Min.·sin(2·d·360°/669,6),

wobei die Berechnung der Amplitude wie folgt lautet:
6,94Sec.·(2/π)·167,4 = 740Sec. = 2·6,16Min.

d ist die Zeit von 0 bis 670 Sol.

4.3 Zeitgleichung

Die Addition der beiden Teilgleichungen (1a) und (2a) ist die gesuchte Zeitgleichung. Sie lautet:

ZG = ZG1 + ZG2 =
      - 42,74Min.·sin((d+34)·360/669,6)
        - 6,16Min.·sin(2·d·360/669,6).

d ist die Zeit von 0 bis 670 Sol.

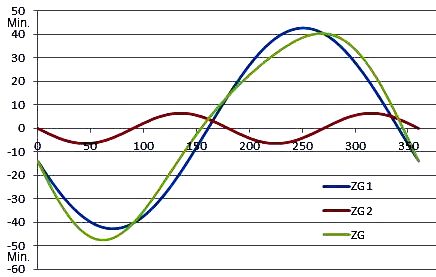<< Abb.7 Zeitgleichung ZG = ZG1 + ZG2 in Min.

Abb.7 zeigt die Zeitgleichungs-Kurve ZG und deren beide Teilkurven ZG1 und ZG2.
Weil die Amplitude von ZG2 relativ klein ist, unterscheidet sich ZG wenig von ZG1.
Die Kurven beginnen zur Wintersonnenwende. Die Zeitachse ist ist über den Winkel eines Kreises (0° bis 360°, entspricht einem Marsjahr von Sol 0 bis Sol 670) skaliert.

4.4 Das Analemma (inkl. Vergleich mit dem der Erde)

In der Abb.8 ist in der Mitte die im Vorherigen ermittelte Zeitgleichung als Analemma dargestellt. Zum Vergleich ist links ein von der NASA veröffentliches Bild, in dem lediglich das Analemma geringfügig breiter ist, beigefügt.

Dem NASA-Bild habe ich für meine Arbeit die gegenwärtige Position des Perihels entnommen: etwa 19 Ekliptik-Winkelgrade vor der Wintersonnenwende (WSW).

Den Vergleich des Mars-Analemma mit dem der Erde ermöglicht das rechts befindliche Erde-Analemma:

1. Das Erde-Analemma ist ein geschlossenes, aber in sich einmal verschlungenes Band wie bei einer Acht (8), während das des Mars Tropfen- bzw. O-Form hat. Diese Formen entsprechen dem jeweiligen Graph der Zeitgleichunmg ZG. Die Verschlingung zu einer 8 besteht, wenn der Graph zwei Maxima/Minima-Paare hat, und verschwindet bei nur einem solchen Paar. Die Reduktion auf nur ein Paar besteht immer, wenn die Amplitude der Teil-Zeitgleichung ZG2 kleiner als die Hälfte der ZG1 ist.
   Beim Mars-Analemma ist das der Fall: momentanes Verhältnis = 6,16 / 42,74 = 0,085 < ½ .
   Beim Erde-Analemma ist das momentane Verhältnis = 9,83 /7,65 = 1,28 > ½ .
2. Das Analemma des Mars ist wegen dessen größerer Bahn-Exzentrizität deutlich breiter als das der Erde.
3. Die Analemmata sind entgegengesetzt und verschieden stark geneigt. Beides wird von der Lage des Perihels im Verlaufe des Jahres bestimmt. Beim Mars liegt das Perihel vor der Wintersonnenwende, bei der Erde danach. Beim Mars beträgt der ekliptikale Winkel zwischen den beiden Ereignis-Orten etwa 19°, bei der Erde nur
   etwa 3° .

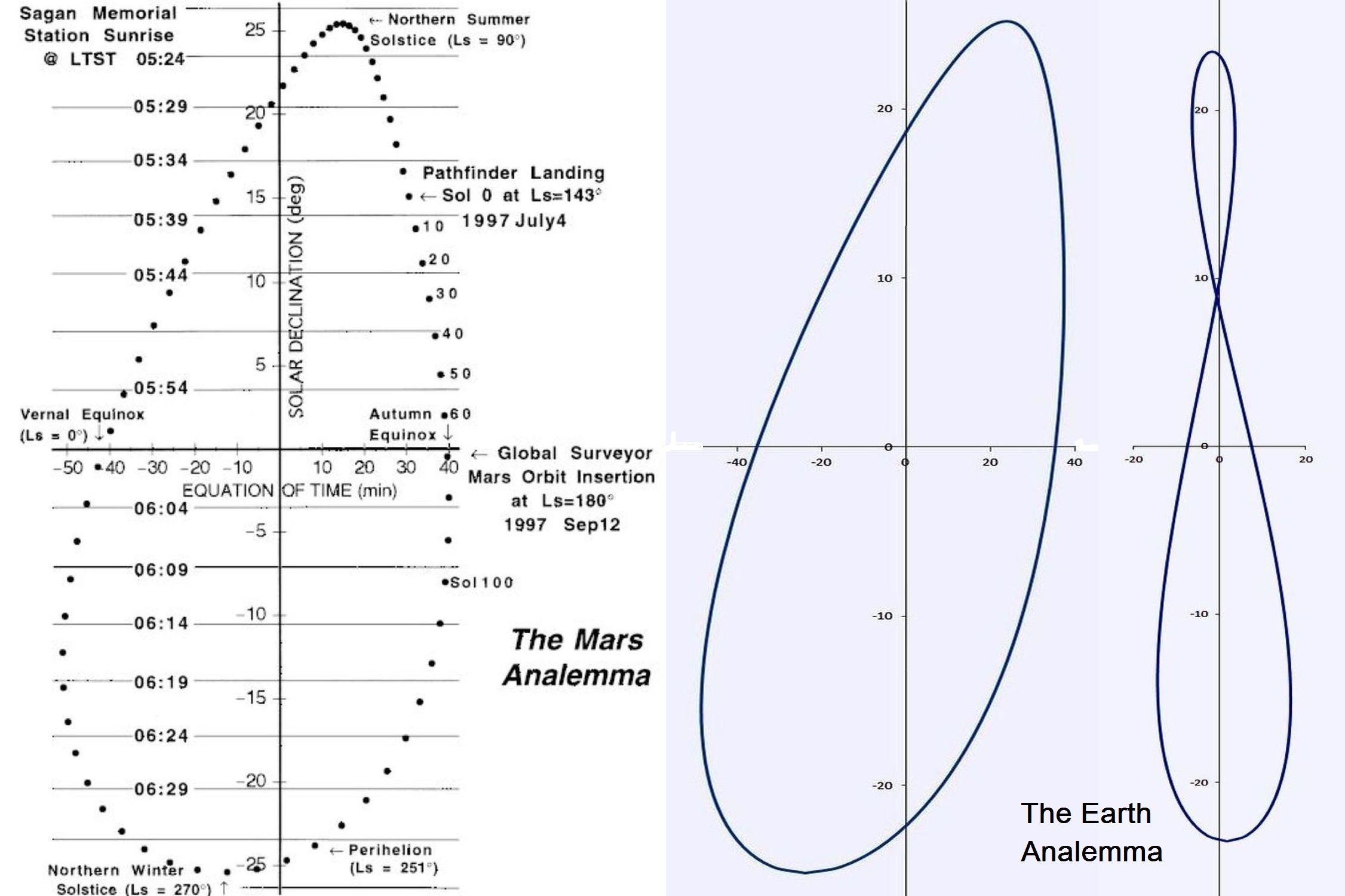Abb.8 Das Analemma des Mars (links und Mitte) und das der Erde (rechts)
          Bild links: NASA

5. Vergleiche mit der Zeitgleichung auf der Erde

Die zum Vergleich verwendeten Zahlen-Werte für die Erde sind dem Artikel "Die Zeitgleichung, elementar behandelt" entnommen (das Gleiche gilt auch für den Abschnitt 4.4 vorher).

5.1 ZG1 (Ursache 1)

In die ZG1 gehen nur die Exzentrizität e der Planeten-Bahnen und für eine Zwischen-Gleichung die Zahl der Eigendrehungen der Planeten pro Jahr ein.

Die Amplituden A der ZGn1 stehen im gleichen Verhältnis wie die relativen Exzentrizitäten e der elliptischen Umlaufbahnen der beiden Planeten:
A_M : A_E = e_M : e_E = 0,0934 : 0,0167 = 5,59 : 1 = 42,74 : 7,65 .       (siehe Gleichungen (1a))

Das Amplituden-Verhältnis der Schwankungen der Tageslängen ΔT₁ (Zwischen-Gleichungen) ist um das Verhältnis der Tage/Sol eines Jahres (667,60 : 365,25 = 1,83 : 1) kleiner:
ΔT_1M : ΔT_1E = 5,59 : 1,83 = 3,05 : 1 = 24,07 : 7,90 .       (siehe Gleichungen (1))
Da die Schwankungen beim Mars auf 1,83-mal mehr Eigendrehungen (beide dauern etwa gleich lang) verteilt sind, schwanken seine Drehungen (1/1,83)-mal weniger, als es der größeren Exzentrizität enspricht. Bei der Aufsummierung zur ZG1 (Integration der Gleichung (1) zu Gleichung (1a)) entfällt der Faktor 1,83 wieder.

5.2 ZG1 (Ursache 2)

In die ZG2 gehen nur die Zahl der Eigendrehungen der Planeten pro Jahr und der Winkel ε für die Schrägstellung der Planeten-Achse auf der Ebene seiner Umlaufbahn ein.

Die Amplituden A der ZGn2 stehen im Verhältnis
A_M : A_E = 1 : 1,60 = 6,16 : 9,83 .       (siehe Gleichungen (2a))

Anstatt 1:1,60 wäre das Verhältnis 1:1,83, also gleich dem Verhältnis der jährlichen Eigendrehungen der beiden Planeten, wenn deren Winkel ε gleich wären (ε=23,44°). Die Vergrößerung auf 1:1,60 wird vom ε-Unterschied verursacht. Diese Veränderung ist nicht linear vom Verhältnis ε_M : ε_E abhängig (Multiplizieren mit diesem Verhältnis wäre falsch), denn die Winkelschwankung Δω in der Äquator-Ebene wird mit zweimalige Anwendung von cos ε berechnet.
cos ε ist keine lineare, sondern eine trigonometrische Funktion von ε .

Das Amplituden-Verhältnis der Schwankungen der Tageslängen ΔT₂ ist wie bei ZG1 um das Verhältnis der Tage/Sol eines Jahres kleiner:
ΔT_2M : ΔT_2E = 1 : (1,60·1,83) = 1 : 2,93 = 6,94 : 20,3 .       (siehe Gleichungen (2))
Bei der Aufsummierung zur ZG2 (Integration der Gleichung (2) zu Gleichung (2a)) entfällt der Faktor 1,83 wieder.

6. Literatur

[1] R.P.Feynman: Die Bewegung der Planeten um die Sonne
     D.L. und J.R.Goodstein: "Feynmans verschollene Vorlesung", 1998 Piper
[2] S.Wetzel: Die Physik der Sonnenuhr,
     Schriften der Freunde alter Uhren, 1998, Abb.13

7. Anmerkungen

Anmerkung 1: Sind die Schwankungen beide Male <<1, was erwartet werden darf, so erscheinen sie im Ergebnis in Näherung als Summe. Man multipliziere z.B.
1,05·1,10 = 1,155   ≈  1,15 = 1+(0,05+0,10).

Anmerkung 2: Von der exakten binomischen Reihe ist nur der letzte Summand ±Δl² weggelassen (#4).
Man quadriere z.B.
1,1² = 1,21 = (1+ 0,1)²  ≈  (1+ 2·0,1) = 1,2.
Dann das Reziproke (#5):
1 / (1+ 0,1)² = 0,826..  ≈  (1- 2·0,1) = 0,8 ,
was auch noch annehmbar wäre, obwohl man 0,1 noch nicht als deutlich <<1 bezeichnen kann.

Anmerkung 3: Vernachlässigt wird dabei, dass Sommer- und Winter-Halbjahr wegen der elliptischen Bahn nicht genau gleich lang sind.

Anmerkung 4: Das exakte, etwas weniger elementare Vorgehen beachtet, dass es sich um sphärische Dreiecke handelt. Wenn man diese halbiert (Abb.2), entstehen rechtwinklige sphärische Dreiecke mit relativ kurzen Ausdrücken:
sin (ω_max/2) = sin (ω₀/2) / sin (90°- ε) = sin (ω₀/2) / cos ε ,
tan (ω_min/2) = tan (ω₀/2)·cos ε .
Wegen der Kleinheit der Winkel ω und ω₀ darf deren Sinus und Tangens durch den Winkel (Bogenmass) selbst ersetzt werden. Das führt auf anderem Wege zu den bereits benutzten Näherungen (#6,#7).

Anmerkung 5: Hier zeigt sich überdeutlich, auf welchen mühsamen Umweg sich Feynman eingelassen hat, elementar vorzugehen und Eleganz und Schönheit geometrischer Beweise höherer Mathematik vorzuziehen.
Den Ausdruck (1) zu integrieren erfordert nämlich viel weniger Geduld und ist ein kurzer Schritt anstatt der vielen Schritte, auf die ich mich auch eigelassen habe.
Die Integration des Ausdruckes (1):
24,1 ∫ cos((d-d₁)·2π/670) dd =
(24,1·670/(2π))·sin((d-d₁)·2π/670) =
2570·sin((d-d1)·360/670) .
Bei Ausführung der Integration musste auf Bogenmass (2π anstatt 360°) gewechselt werden, weil sonst anstatt 670/2π ein falscher Integrationsfaktor entstanden wäre. Mit 2570 Sec. = 42,8 Min. und unter Berücksichtigung der Vorzeichenfestlegung bei der Zeitgleichung lautet das Ergebnis:
(1a)   ZG1 = -42,8Min.·sin((d-d₁)·360/670) .

Anmerkung 6: Die von einer reinen Sinus- oder Cosinus-Halbwelle begrenzte Fläche ist tatsächlich genau 2, wie folgendes bestimmte Integral in den Grenzen von π/2 bis 3π/2 zeigt:
∫ cos x dx = [sin x] = sin (3π/2) - sin (π/2) = -2 .
Das negative Vorzeichen deutet an, dass die Fläche unterhalb der Null-Linie liegt.

Siegfried Wetzel, CH 3400 Burgdorf, November 2025

 ↑↑ Anfang
<< andere Sonnenuhren-Beiträge     << Home