<< Home
<< andere Sonnenuhren-Beiträge
↓↓ Ende
Die Zeitgleichung, elementar behandelt
DGC-Mitteilungen Nr.109, 2007 / Chronométrophilia No 62, 2007
Korrigenda: In der ersten der beiden Veröffentlichungen ist in den Gleichungen (2) und (2a) ein Teilungsfehler enthalten.
Inhalt
1. Einleitung2. Zeitgleichungs-Ursachen
3. Schwankung der Tageslänge
4. "Nach- und Vorgehen" der Sonnenuhr
5. Genauigkeit von Zeitgleichungen
6. Literatur
7. Anmerkungen
1. Einleitung ↑ Anfang
Der amerikanische Physiker Richard Feynman hielt eine ungewöhnliche Vorlesung für Studienanfänger mit dem auch für die Zeitgleichung bedeutsamen Titel "Die Bewegung der Planeten um die Sonne " [1]. Ungewöhnlich daran war, dass er den darin enthaltenen Ellipsen-Beweis elementar führte. Mit elementar meinte er, dass zum Verständnis wenig Vorwissen, allerdings viel Intelligenz nötig sei. Er leitete den Satz mit vorwiegend geometrischen Überlegungen her, denn Eleganz und Schönheit geometrischer Beweise spreche viele Menschen an. Nachteil sei, dass man anders als bei Verwendung höherer Mathematik mit Geduld viele Schritte machen müsse. Richard Feynman's Vorlesung ist Vorbild für die folgende Behandlung der Zeitgleichung. Der von ihm verwendete Begriff elementar wird im Folgenden kursiv geschrieben.
Die zu findende Zeitgleichung ist für den Gebrauch bei einer Sonnenuhr gedacht. Sie darf deshalb einige astronomische Tatsachen mit geringem Einfluss ausser Acht lassen. Und bei der Herleitung dürfen Vereinfachungen erfolgen. Die viel genauere, d.h. umfassendere und exaktere wissenschaftliche Bearbeitung erfährt nämlich beim "Hausgebrauch" - das ist seine Anwendung beim Ablesen einer gewöhnlichen Sonnenuhr - nicht die ihm zustehende Würdigung. Eine solche Uhr kann man nicht genauer als auf eine Minute ablesen.
Dass die Zeitgleichung nicht jährlich neu berechnet werden muss, wird von der Tatsache bestärkt, dass viele Sonnenuhren mit deren Werten oder Kurven auf Dauer versehen sind. Geheimnis bleibt aber oft, wie man diese Werte oder Kurven berechnen kann. Im Folgenden wird das auf elementare Weise gezeigt. Glücklicherweise lassen sich dabei einige Vereinfachungen machen, so dass die Zahl der Schritte nicht allzu gross und die Geduld beim Lesen nicht zu sehr beansprucht wird. Sollte dem Leser die eine oder andere Vereinfachung als zu riskant erscheinen, so hat er am Ende doch zu einer Zeitgleichung gefunden, die sich "mit blossem Auge" betrachtet nicht vom bekannten Ergebnis aus einer nicht elementaren wissenschaftlichen Arbeit unterscheidet. Einer solchen Arbeit zu folgen, hätte aber ein höheres Mass an Mathematik und - was gleich gewichtig ist - ziemlich viele astronomische Insider-Kenntnisse vorausgesetzt.
2. Zeitgleichungs-Ursachen ↑ Anfang
Nicht beachtet werden die sehr langsamen Veränderungen am Sonnenhimmel, wie Form und Lage der Erdbahn-Ellipse, Jahr-Länge(n), Neigung der Erdachse u.ä.. Ausgewertet werden die bekannten Ursachen für das "Falsch-Gehen" der Sonnenuhr. An diese sei kurz erinnert.
Die Erde muss sich pro Tag mehr als einmal um sich selbst drehen. Nach einer 360°-Drehhung ist erst ein Sterntag vollendet. Die (von der Sonne überstrahlten) Sterne stehen wieder am selben Ort (Süden, Meridian), die Sonne ist aber wegen der kurzen Bahnfahrt der Erde noch nicht dort angekommen. Deshalb muss sich die Erde zur Vollendung des Sonnentages noch ein Stück weiter drehen (Abb.1). Zwei Ursachen bewirken, dass das täglich unterschiedlich lange dauert.
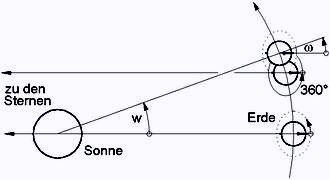
<< Abb.1 tägliche Bahnfahrt und Eigen-Drehung der Erde
Ellipse (1. Ursache: variabler Bahnwinkel): Auf der schwach elliptischen Erdbahn ist der Abstand der Erde zur Sonne variabel. In Sonnennähe ist der tägliche Bahnwinkel w größer als in Sonnenferne. Die ihn kompensierende Zusatzdrehung ω der Erde muss in einer Hälfte des Jahres grösser, in der anderen Hälfte kleiner sein, weshalb in diesen Zeiten der Tag länger bzw. kürzer als im Durchschnitt ausfällt.
Ekliptik (2. Ursache: variables Verhältnis zwischen Bahnwinkel und zusätzlichem Drehwinkel): Die Richtung der Drehachse der Erde ist im Weltraum fix und nicht rechtwinklig zur Erdbahnebene, weshalb sich das Verhältnis zwischen dem Bahnwinkel w und dem um die schiefe Erdachse erfolgenden Drehwinkel ω täglich ändert. Zur Zeit der Sonnenwenden ist ω grösser(ωmax) als der zu kompensierende tägliche Bahnwinkel wo (Abb.2, links). Zur Zeit der Tag/Nacht-Gleichen ist ω kleiner (ωmin; Abb.2, rechts). Die Wirkung der zweiten Zeitgleichungs-Ursache lautet kurz formuliert: Die tägliche Bahnfahrt der Erde führt nicht 1:1 zu ihrer täglichen Zusatzdrehung. In zwei Vierteln des Jahres ist das Verhältnis grösser, in den beiden Vierteln dazwischen kleiner mit den entsprechenden Auswirkungen auf die Tageslänge.
 Abb.2 Winkelunterschiede zur Sonnenwende (links) und zur Tag/Nacht-Gleiche (rechts) [2]
Abb.2 Winkelunterschiede zur Sonnenwende (links) und zur Tag/Nacht-Gleiche (rechts) [2]
3. Schwankung der Tageslänge ↑ Anfang
Schwankungen sind relative Angaben zu einer mittleren Grösse. Kleine (<<1) periodische Schwankungen lassen sich in guter Näherung (Näherung #1) mit einer Kreisfunktion (Sinus-, Cosinus-) beschreiben, für die dann nur Amplitude, Periodendauer und Nullpunkt zu bestimmen sind.
Die Wirkungen der beiden Ursachen wären eigentlich miteinander zu multiplizieren. Weil aber beide Schwankungen klein sind, erscheinen sie im Ergebnis in Näherung als Summe (#2, Anmerkung 1). Deshalb ist es möglich, beide Ursachen getrennt zu behandeln und erst am Schluss die Summe aus ihren Wirkungen zu bilden.
Ellipse (1. Ursache)
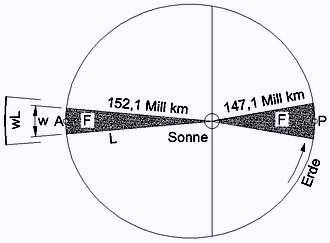 << Abb.3 zweites Keppler'sches Gesetz
<< Abb.3 zweites Keppler'sches Gesetz
Das zweite Keppler'sche Gesetz lautet: Die Verbindungslinie eines Planeten (die Erde ist einer ) mit der Sonne überstreicht in gleichen Zeitabschnitten gleich grosse Flächen (Abb.3). Der im Folgenden zu betrachtende Zeitabschnitt ist der Tag, die Flächen F sind wesentlich kleiner (spitzer) als abgebildet.
Abstände:
(mittlerer) L0 ( = 149,56·106 km)
(variabler) L ( = L0 ± ΔL = 149,56·106 ± 2,498·106 km)
(relativer) l ( = L/L0 = 1 ± ΔL/L0 = 1 ± Δl = 1 ± 0,0167)
Δl = 0,0167 ist die numerische Exzentrizität
der elliptischen Bahn.
Der tägliche Bahnwinkel w beträgt nur ca.1°
(pro Jahr eine ganze Bahnrunde =360°):
Sein Mittelwert ist:
w0 = 360°/365,2422Tage = 0,9856°/Tag.
Die nächste Zeile enthält eine weitere Näherung (#3: Bahnstück als Kreisbogen wL angenommen; bei ganzem Kreis käme man mit 2πL (Umfang) auf FK=πL2, die bekannte Kreisfläche.):
F = wL·L/2 = wL2/2 (w im Bogenmass, Abb.3).
Nun weiter: w = 2F/L2, und weiter: w0 = 2F/L02 (Mittelwert des täglichen Bahnwinkels).
Und nun relativ zu w0, also die Schwankung des täglichen Bahnwinkels w:
w/w0 = L02/L2 = 1/l2 = 1/(1± Δl)2 .
Weil Δ<<1 sind zwei weitere Näherungs-Schreibweisen möglich (Anmerkung 2):
#4: (1± Δl)2 = (1± 2Δl).
#5: 1/(1± 2Δl) = (1 ∓ 2Δl) ; Kehrwert, d.h. Vorzeichenwechsel.
Neue Schreibweise:
w/w0 = 1 ∓ 2Δl .
Gleich wie die Schwankung des täglichen Bahnwinkels w ist die Schwankung
der Zeit T1 für den täglichen Zusatz-Dreh der Erde:
T1/T0 = 1 ± ΔT1 = 1 ∓ 2Δl = 1 ∓ 0,0334 .
die Bezugszeit ist:
T0 = 24 std·w0 /(w0 +360°) = 236 sec ,
und damit:
ΔT1 = 2Δl ·T0 = ∓ 7,88 sec .
Der Tag ist in Perihelnähe (P) ca.8 sec länger als im Mittel und in Nähe des Aphel (A) ca.8 sec kürzer. Seine ganzjährige Schwankung aus Ursache 1 lässt sich mit folgender Cosinus-Funktion beschreiben (#1, Anmerkung 3):
(1) 7,9sec·cos((d-d1)·360°/365) (Abb.4).
d ist die Zeit von 0 (1.Jan. 0h) bis 365 (31.Dez. 24h) Tage, (der Schalttag alle 4 Jahre wird übersprungen). Der zeitliche Nullpunkt ist ab Jahreswechsel um d1=3 Tage in die Zukunft verschoben. Das ist der Tag des Perihel-Durchgangs.
Ekliptik (2. Ursache)
Der tägliche Bahnwinkel w würde 1 : 1 vom in der Äquator-Ebene für die Zeitmessung zu bestimmenden Drehwinkel ω kompensiert, wenn die Erdachse senkrecht auf ihr angeordnet wäre: w = ω (Abb.1).
Wegen der Achs-Schräge erscheint der Bahnwinkel aber als Bogenstück eines Großkreises auf der Erdoberfläche, der gegen die Äquator-Ebene geneigt ist (Abb.2). Zu ermitteln ist der zugehörige Drehwinkel ω, der ein Stück des Äquatorkreises ist. Wegen (#1) genügen Grösst- und Kleinstwert dieses Winkels.
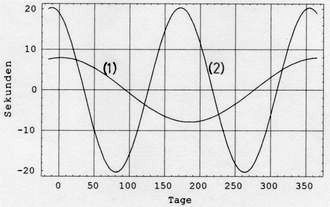
<< Abb.4 Schwankungen der Tageslänge
Grösstwert, Sonnenwenden (Abb.2, links):
Das w0 entsprechende Bogenstück auf der Erde ist Teil des Ekliptik-Kreises. Da es klein ist, darf es durch ein Stück des Wendekreises (ein Kleinkreis) ersetzt werden (#6). w0 steht dann zu ωmax im gleichen Verhältnis wie die Radien von Wende- und Äquatorkreis. Dieses lautet:
w0/ωmax = cos ε .
Mit den Werten für w0 und ε = 23,44°ist der Größtwert:
ωmax = w0 /cos ε = 1,07425° .
Kleinstwert, Tag/Nacht-Gleichen (Abb.2, rechts):
Das sphärische Doppel-Dreieck aus w0, ε und ωmin ist klein genug, dass es als ebenes Dreieck angesehen werden darf (#7). Mit ebener Trigonometrie gilt die Beziehung
cos ε = (ωmin/2)/(w0/2), und der Kleinstwert ist:
ωmin = w0·cos ε = 0,90427°.
Mit sphärischer Trigonometrie lassen sich die Werte exakt bestimmen (Anmerkung 4), man findet aber bei der gewählten Auflösung noch
keinen Unterschied.
Die Verarbeitung der beiden Werte führt zu:
mittlerer Wert ω0 = 0,98926° ,
ω = 0,98926° ± 0,08499° und
ω/ω0 = 1 ± Δω = 1 ± 0,08591 .
Die Drehgeschwindigkeit der Erde ist konstant. also schwankt die Tageslänge T2 wie der Drehwinkel ω:
T2/T0 = 1 ± ΔT2 = 1 ± Δω
Mit T0 = 236 sec ist ΔT2 = Δω·T0 = ± 20,3 sec .
Der Tag ist an den Sonnenwenden ca. 20 sec länger als im Mittel, an den Tag/Nacht-Gleichen ca. 20 sec kürzer. Seine halbjährige Schwankung aus Ursache 2 lässt sich mit folgender Cosinus-Funktion beschreiben (#1):
(2) 20,3sec·cos(2·(d-d2)·360°/365) (Abb.4)
Von den beiden Sonnenwenden liegt die des Winters am nächsten beim Jahreswechsel. Der zeitliche Nullpunkt ist ab Jahreswechsel um d2=-10 Tage in die Vergangenheit verschoben.
4. "Vor- und Nachgehen" der Sonnenuhr ↑ Anfang
Aus schon genannten Gründen können die Effekte getrennt voneinander behandelt werden, was auch weiter gelten soll.
Folgen beispielsweise Tage aufeinander, die zu kurz sind, so geht die Sonnenuhr schneller als die "Normaluhr" und eilt ihr schliesslich voraus. Sie geht erst wieder langsamer, wenn längere Tage folgen und beginnt nachzugehen, wenn genügend lange Tage vergangen sind. Die Addition vergangener Abweichungen von der mittleren Tageslänge (24 std) ist der Wert des "Falsch-Gehens", den die Zeitgleichung für den betroffenen Tag angibt.
Ellipse (1. Ursache)
In Abb.5 sind die Verkürzungen aus Ursache 1 zwischen 94. und 277.Tag des Jahres (in der mittleren Hälfte des Jahres) jeden 5.Tag mit einem Balken gekennzeichnet. Denkt man sich in die Lücken weitere Tages-Balken gezeichnet, so ist zwischen der Kurve der Gleichung (1) und der Null-Linie eine gefüllte Fläche entstanden. Sie enthält die Summe aller Verkürzungen in diesem Zeitraum (918sec), die der Sonnenuhr von grösstem Nachgehen (-7,65min) zu grösstem Vorgehen (+7,65min) verhilft. Letzteres zeigt die in Abb.5 auch enthaltene Kurve ZG1 die wegen (#1) eine Sinus-Linie ist. Weil die Steigung hier (Perioden-Mitte) positiv ist, handelt es sich um den negativen Sinus.
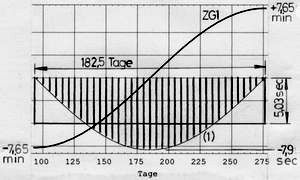
<< Abb.5 Sonnenuhr-"Vorgehen" an zu kurzen Tagen
Wie findet man die angegebenen Zahlen-Werte?
Man könnte die Balken-Werte ausrechnen und addieren. Diese Zeitsumme kann aber auch mit Hilfe einer geometrische Näherung (#8) ermittelt werden (Anmerkung 5). In Abb.6 wird die Kurve M ((1) in Abb.5) von den Kurven K und G eingerahmt (die Amplitude alle drei ist 1; die Skalierung der Zeitachse ist Bogenmaß). Der Halbkreis K enthält die kleinere Fläche (FK=π/2), und die Halb-Ellipse G als gestreckter Halbkreis enthält die grösseren Fläche (FG=π2/4, Streckung im Verhältnis π:2).
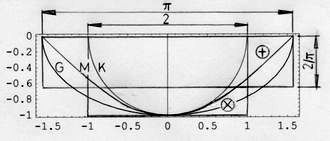
<< Abb.6 geometrische Näherung einer Cosinus-Fläche
Der Mittelwert aus beiden kann als die gesuchte Fläche angenommen werden: FM = (FK+FG)/2 = 2,02. Weiter wird mit dem runden Wert 2 gerechnet, der sich auch anbietet bei Näherung der gesuchten Fläche durch das Rechteck 2 mal 1. Die beiden Eck-Flächen Ä und Å scheinen gleich gross zu sein (Anmerkung 6). Das schmale Ersatz-Rechteck hat folglich die "Amplitude" 2/π. In der Fläche von Abb.5 ist die Amplitude nicht 1 sondern 7,9sec, die beim Rechteck zu 5,03sec (7,9sec·(2/π)) wird. Die Fläche stellt also 5,03sec·182,5 = 918sec = 2·7,65min dar, wie oben angegeben.
Die Amplitude (7,65 min) und die Phasenlage (negativer Sinus) des elliptischen Teils der Zeitgleichung sind somit gefunden. Die Teilgleichung lautet:
(1a) ZG1 = - 7,65min·sin((d-3)·360°/365).
Ekliptik (2. Ursache)
Zum Vor -und Nachgehen der Sonnenuhr infolge Ursache 2 kommt man mit Überlegungen, die analog zu obigen sind. Die Cosinus-Kurve (2) mit Amplitude 20,3 sec und der Periode von 182,5 Tagen führt zur negativen Sinus-Kurve, der zweiten Teilgleichung
(2a) ZG2 = - 9,83min·sin(2·(d+10)·360°/365);
wobei die Berechnung der Amplitude wie folgt lautet:
20,3sec·(2/π)·91,25 = 1180sec = 2·9,83min .
Zeitgleichung
Die Addition der beiden Teilgleichungen (1a) und (2a) ist die gesuchte Zeitgleichung. Sie lautet:
ZG = ZG1 + ZG2 =
= - 7,65min·sin((d -3)·360°/365)
- 9,83min·sin(2·(d+10)·360°/365) .
d ist die Zeit von 0 bis 365 Tage (der Schalttag alle 4 Jahre wird übersprungen). Üblicherweise werden nur für einen Moment (12h) eines Tages Werte ausgerechnet und als Näherung für den ganzen Tag benutzt. In die obige Gleichung ist d=0,5 (1.Januar,12h) usw. bis d=364,5 (31.Dezember,12h; der Schalttag alle 4 Jahre wird übersprungen) einzusetzen.
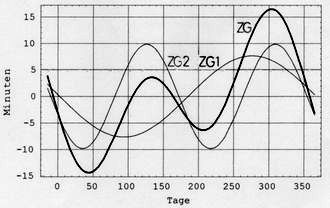
<< Abb.7 Zeitgleichung ZG = ZG1 + ZG2
Abb.7 zeigt die bekannte Zeitgleichungs-Kurve und deren beide Teilkurven. Weil die Teilkurven keinen gemeinsamen besonderen Punkt haben, gibt es in der Addition keine Symmetrie. Eine solche würde sich ergeben, wenn z.B. Perihel (für ZG1) und Wintersonnenwende (für ZG2) am gleichen Tage stattfänden. Dann hätten die beiden Hauptmaxima und die beiden Nebenmaxima in der Addition je gleiche Amplituden. Das war im Jahre 1246 so.
Die Amplituden der beiden Kurven in Abb.4 haben ungefähr das Verhältnis 1:2,5. In Abb.7 ist es aber nur noch ungefähr 1:1,25. Die Schwankung der Tageslänge aus Ursache 2 hat in der Zeitgleichung nämlich nur die proportional halbe Wirkung im Vergleich zu der aus Ursache 1, weil ihre Periodenlänge nur halb so gross ist. Wegen unpassender Phasenlage der beiden Ursachen zueinander gibt es keinen Tag, an dem sich deren Größtwerte addieren, was in Abb.4 ca.28 sec, in Abb.7 ca.17,5 min ergäbe.
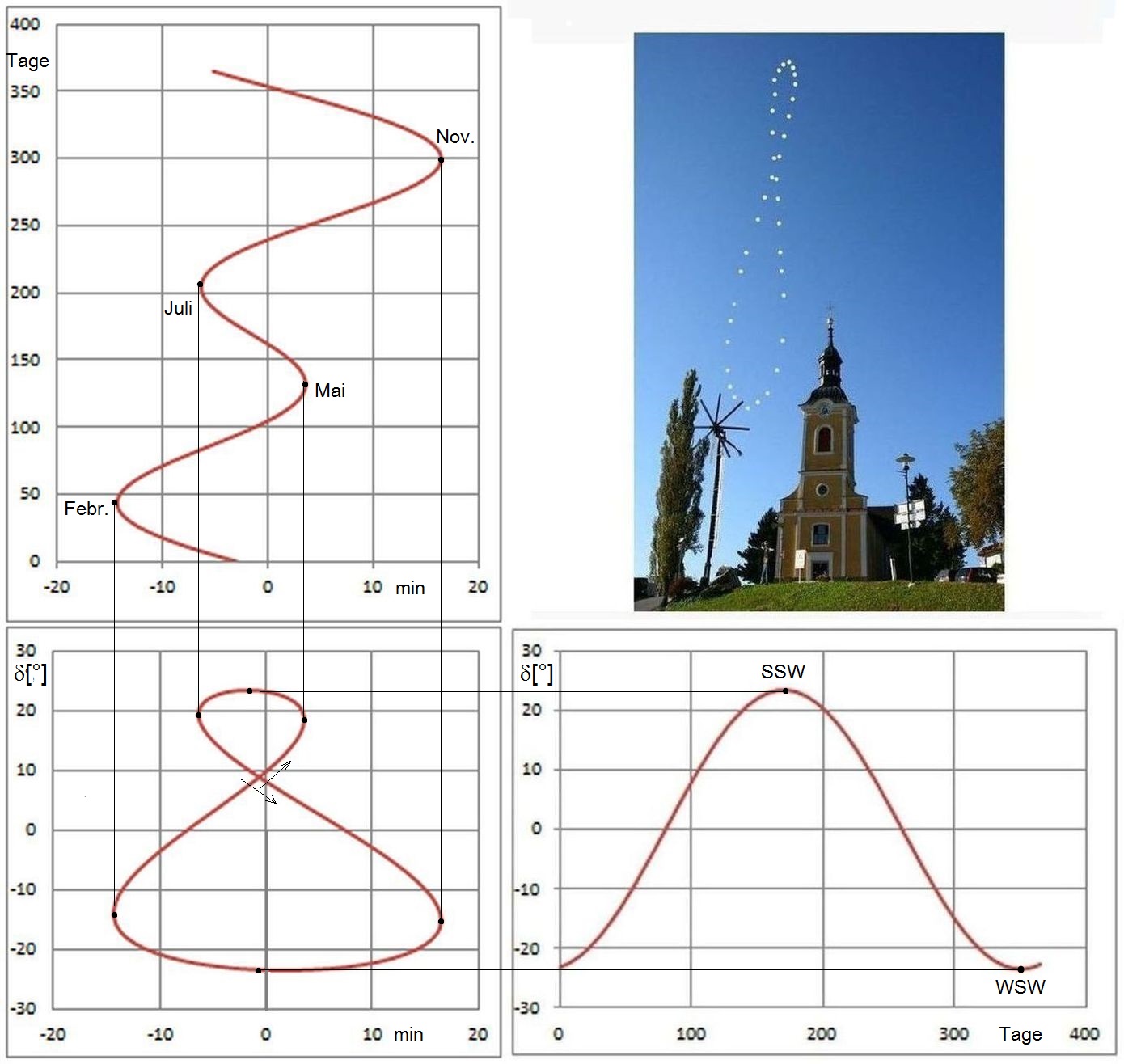 Abb.8 Darstellung der Zeitgleichung aus Abb.7 (hier mit getauschten Achsen, links oben),
Abb.8 Darstellung der Zeitgleichung aus Abb.7 (hier mit getauschten Achsen, links oben),
der Sonnendeklination δ (rechts unten) und das mit Hife beider konstruierte Analemma (links unten)
rechts oben: das vom Sonnenstand über ein Jahr gebildete Analemma (Montage aus jeweils zur gleichen Uhrzeit
(MEZ) aufgenommenen Fotos, astrofotos.at)
5. Genauigkeit von Zeitgleichungen ↑ Anfang
Die gefundene Zeitgleichung ist für den Gebrauch an Sonnenuhren über viele Jahre brauchbar, denn ihre Tageswerte weichen weniger als eine Minute von genauen über Jahrzehnte berechneten Mittelwerten ab. In der aus [3] entnommenen Tabelle sind einige mit ihr für ein Normaljahr berechneten Werte zum Vergleich eingetragen (Abb.9). Der Sonnenuhren-Freund möge sich aber an die Original-Tabelle [3] halten (ihre Werte praktischerweise auf volle Minuten runden) und sich nur zum Vergleich jährlich die besten Werte beschaffen [4]. Dabei erhält er infolge des Schaltjahr-Rhythmus' ab dem fünften Jahr einen Tabellen-Satz, der sich nicht mehr als 1 Sekunde vom ersten unterscheidet. Also könnte man sogar bei erhöhten Ansprüchen mit einem Satz von 4 Tabellen auskommen, auch deshalb, weil Berechnungen in die weite Zukunft gar nicht so sicher sind. Sie beruhen auf heute bekanntem Wissen zu sehr langsamen Veränderungen im Himmel, die laufend beobachtet werden und von Zeit zu Zeit zur Änderung des genauen Rechenschemas führen.
Relevante Himmelserscheinungen (Perihel, Wintersonnenwende u.a.) verspäten sich über 1 Jahr ca.1/4 Tag. Ab dem Schalttag im vierten Jahr erscheinen sie täglich ca.3/4 Tage früher als im dritten Jahr. Diese Verschiebungen bewirken die grössten, aber praktisch immer noch nicht störenden Veränderungen (< 1/4 min) in der Zeitgleichung. Folgende Überlegung lässt den Gebrauch derart genauer Zeitgleichungs-Werte für eine Sonnenuhr sogar absurd erscheinen: In den Tabellen ist nämlich für einen Tag immer nur ein Wert ( für Mittag, 12h ) angegeben. Zu anderen Tageszeiten kann die reale Abweichung aber grösser sein als der Unterschied zur vorherigen oder nachfolgenden Jahrestabelle.
Die elementar und näherungsweise hergeleitete Zeitgleichung erfüllt ihren Zweck, den Verlauf übers Jahr zu zeigen und die richtige Grössenordnung (insbesondere der Extremwerte) anzugeben. Die Nulldurchgänge liegen manchmal 1 Tag daneben, was aber nicht heisst, dass die Genauigkeit hier schlechter wäre. Das ist nur auffälliger als bei den Tagen der Extremwerte und unschön, denn man wäre gern auf je einen "richtigen" Tag gekommen. Aber auch bei genauer Rechnung springen diese Daten im Schaltjahr-Rhythmus einen Tag hin und her.
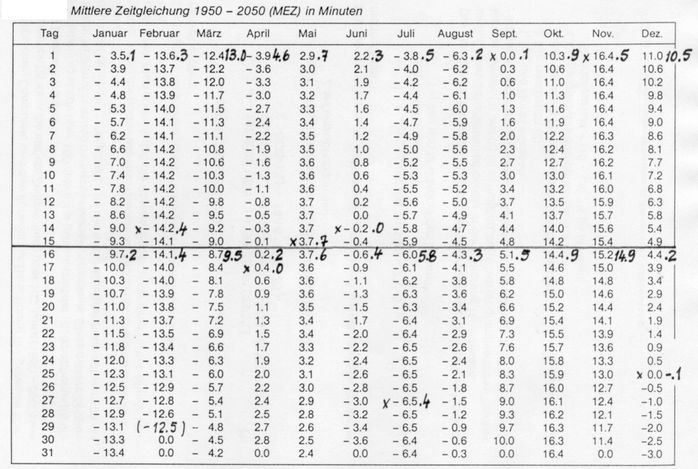 Abb.9 Zeitgleichungs-Tabelle [3]; Hand-Einträge: mit obigen Gleichungen berechnete Werte
Abb.9 Zeitgleichungs-Tabelle [3]; Hand-Einträge: mit obigen Gleichungen berechnete Werte
für 1. u. 16. Tag jeden Monats und bestimmte Tage (x : Extreme und Nulldurchgänge)
6. Literatur ↑ Anfang
[1] R.P.Feynman: "Die Bewegung der Planeten um die Sonne" in D.L. und J.R.Goodstein:
"Feynmans verschollene Vorlesung", 1998 Piper
[2] S.Wetzel: "Die Physik der Sonnenuhr", Schriften der Freunde alter Uhren, 1998, Abb.13
[3] H.-S.Klausmann: "Die mittlere Zeitgleichung über 100 Jahre", Schriften der Freunde alter Uhren, 1990
[4] Deutsche Gesellschaft für Chronometrie: "Sonnenuhren Handbuch", Anhang auf CD, 2006
7. Anmerkungen ↑ Anfang
Anmerkung 1: Sind die Schwankungen beide Male <<1, was erwartet werden darf, so erscheinen sie im Ergebnis in Näherung als Summe. Man multipliziere z.B.
1,05·1,10 = 1,155
≈ 1,15 = 1+(0,05+0,10). ↑ zurück
Anmerkung 2: Von der exakten binomischen Reihe ist nur der letzte Summand ±Δl2 weggelassen (#4). Man quadriere z.B.
1,12 = 1,21 = (1+ 0,1)2 ≈ (1+ 2·0,1) = 1,2.
Dann das Reziproke (#5):
1 / (1+ 0,1)2 = 0,826.. ≈ (1- 2·0,1) = 0,8 ,
was auch noch annehmbar wäre, obwohl man 0,1 noch nicht als deutlich <<1 bezeichnen kann. ↑ zurück
Anmerkung 3: Vernachlässigt wird dabei, dass Sommer- und Winter-Halbjahr wegen der elliptischen Bahn nicht genau gleich lang sind. ↑ zurück
Anmerkung 4: Das exakte, etwas weniger elementare Vorgehen beachtet, dass es sich um sphärische Dreiecke handelt. Wenn man diese halbiert (Abb.2), entstehen rechtwinklige sphärische Dreiecke mit relativ kurzen Ausdrücken:
sin (ωmax/2) = sin (ω0/2) / sin (90°- ε) =
sin (ω0/2) / cos ε ,
tan (ωmin/2) = tan (ω0/2)·cos ε .
Wegen der Kleinheit der Winkel ω und ω0 darf deren Sinus und Tangens durch den Winkel (Bogenmass) selbst ersetzt werden. Das führt auf anderem Wege zu den bereits benutzten Näherungen (#6,#7). ↑ zurück
Anmerkung 5: Eleganter aber nicht elementar wäre, den Ausdruck (1) zu integrieren:
7,9sec ∫ cos((d-d1)·2π/365) dd =
(7,9·365/2π)sec·sin((d-d1)·2π/365) =
7,65min·sin((d-d1)·360°/365) .
Bei Ausführung der Integration musste auf Bogenmass (2π anstatt 360°) gewechselt werden, weil sonst anstatt 365/2π ein falscher Integrationsfaktor entstanden wäre. Unter Berücksichtigung der Vorzeichenfestlegung bei der Zeitgleichung lautet das Ergebnis:
(1a) ZG1 = -7,65min·sin((d-d1)·360°/365) . ↑ zurück
Anmerkung 6: Die von einer reinen Sinus- oder Cosinus-Halbwelle begrenzte Fläche ist tatsächlich genau 2, wie folgendes bestimmte Integral in den Grenzen von π/2 bis 3π/2 zeigt:
∫ cos x dx = [sin x] = sin (3π/2) - sin (π/2) = -2 .
Das negative Vorzeichen deutet an, dass die Fläche unterhalb der Null-Linie liegt. ↑ zurück
![]() Siegfried Wetzel, CH 3400 Burgdorf, Dezember 2008 (Jan.11 / März 11 / Juni 14 / März 24 / Nov.25)
Siegfried Wetzel, CH 3400 Burgdorf, Dezember 2008 (Jan.11 / März 11 / Juni 14 / März 24 / Nov.25)
↑↑ Anfang
<< andere Sonnenuhren-Beiträge
Druck-Version (2008, 2-spaltig, 6 Seiten, *.pdf, 950 kB) >>
<< Home