<< Home Der Modulor
Der Architekt Le Corbusier stellte zwei Reihen von Längen-Normalen auf, die er zur Verwendung bei der Dimensionierung jedweder Objekte empfahl. Er veröffentlichte diese unter dem Titel Der Modulor, ein in Architektur und Technik allgemein anwendbares harmonisches Maß im menschlichen Maßstab [1]. Dabei dachte er zuerst an die Werke von Menschen seinesgleichen, die wie er nicht nur als Architekt, sondern auch als Städtebauer, Bildhauer, Maler und Typograph arbeiteten. Danach erweiterte er seine Empfehlung auf die Gestaltung sämtlicher technischer Erzeugnisse.
Le Corbusier betont, dass seine Reihen Fibonacci-Folgen seien. Damit hat er aber nichts Besonderes geschaffen, denn der Quotient zwischen zwei aufeinander folgenden Fibonacci-Zahlen ist von "mathematischer Natur" aus eine Näherung an den Quotienten des Goldenen Schnitts. Diese Näherung ist umso besser, je größer die darin enthaltenen Zahlen sind (im Modulor werden relativ große Zahlen verwendet). Formal hat Le Corbusier sogar Unrecht, denn als Fibonacci-Folgen werden nur Folgen ganzer Zahlen (natürliche Zahlen) bezeichnet.
Anwendung der Renard-Serien
Die Werte der in der Technik gängigen Renard-Serien werden rein seriell angewendet, während Le Corbusier die Modulor-Werte in beliebigen Zusammenstellungen benutzte. Mit Renard-Serien werden Folgen aus ähnlichen Teilen (z.B. Schrauben) und Formen (z.B. Hohlformen wie Bohrungen) erstellt. Die dabei verwendete geometrische Abstufung ist insofern sinnvoll bzw. erforderlich, weil benachbarte größere Teile bzw. Formen in gleichem Verhältnis wie benachbarte kleinere Teile zueinander stehen "müssen". Das Muß ergibt sich aus dem Gebrauch. Bei linearer Abstufung würden die größeren Teile bzw. Formen einander immer gleicher. Sie besäßen keinen unterschiedlichen Gebrauchs-Nutzen mehr. Anwendung des ModulorDie Situation für die Anwendung der Modulor-Reihen ist in der Architektur (wofür der Modulor primär gedacht war) deutlich anders als für die Renard-Serien in der Technik. Es gibt zumindest keine von Architekten zu entwerfende Bauwerk-Serien, wobei sich die einzelnen Bauwerke lediglich in ihrer Größe unterscheiden. In geometrischen Reihen angebrachte Teile oder Formen wären in den Bauwerken vermutlich auch eher eine Ausnahme. Le Corbusier legte die Modulor-Werte wohl als Glieder zweier geometrischen Folgen fest, nennt aber als primären Nutzen die Möglichkeit, dass die Werte aus beiden Reihen in beliebiger Zusammenstellung angewendet werden können. Wie jedem Architekt oder anderem Künstler war es ihm ein driftiges Anliegen, den Goldenen Schnitt im Modulor zu integrieren. Wenn allerdings eine Form mit enthaltenem Goldenen Schnitt zu verwirklichen ist, so kann nicht beliebig kombiniert werden, es müssen zwei benachbarte Werte einer der beiden Reihe angewendet werden. Was bleibt vom Modulor?
Le Corbusier hat gleich wie Renard die unendlich große Menge von Zahlen auf eine begrentzte Menge von Normzahlen reduziert. Renards Normzahlen wiederholen sich in praktisch vorteilhafter Weise im nächst-größeren Dezimalbereich mit zehn mal größeren Werten. Den Modulor-Zahlen fehlt diese vorteihafte Besonderheit, weil einerseits eine dafür unpassende willkürliche (Körpergröße 183 cm) Zahl dazugehören muss, und weil der Goldene Schnitt als Quotient der geometrischen Folgen dafür ungeeignet ist. Le Corbusier grenzt die Zahl möglicher Längemaße an einem architektonisch gestalteten Bauwerk ein, ohne dass daraus ein wirtschaftlicher Vorteil wie bei der Herstellung von und beim Handel von technischen Massenprodukten resultiert. Architektonisch gestaltete Werke sind keine Massenware. Für Betrachter mit künstlerisch geschulten Augen haben sie besonderen Wert, wenn in einigen ihrer Formen der Goldene Schnitt zu erkennen ist. Dafür müssen aber nicht alle der an ihnen vorkommenden Abmessungen aus den beiden Modulor-Reihen stammen. Im Grunde müssen sich die Abmessungen garnicht an den Modulor halten, denn der Goldene Schnitt verlangt keine besonderen absoluten Werte. Literatur[1] Le Corbusier: Der Modulor - Darstellung eines in Achitektur und Technik allgemein anwendbaren harmonischenMaszes im menschlichen Maszstab, 1953, J.G. Cotta'sche Buchhandlung Nachfolger, Stuttgart, Original 1948 in Französisch [2] Le Corbusier: Modulor 2 - 1955 - Fortsetzung von "Der Modulor" 1948, 1958, Deutsche Verlags-Anstalt, München
|
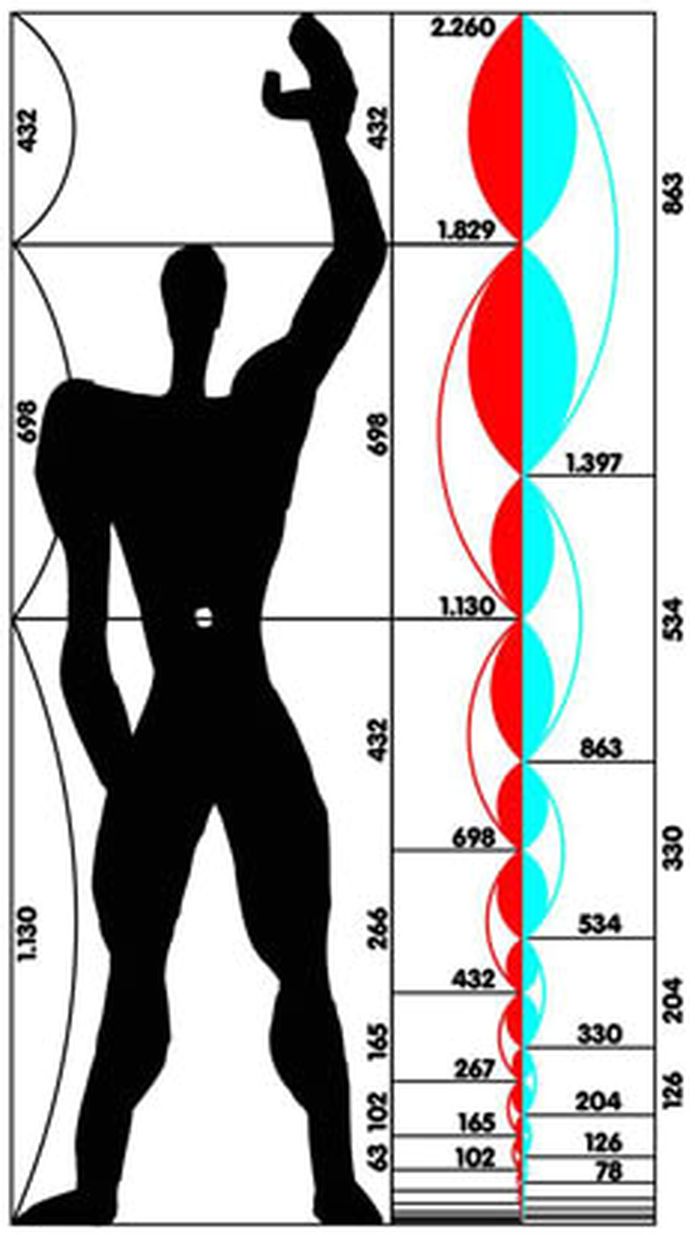Abb.: Der Modulor [