<< Home
<< andere "Rechnen"-Beiträge
 ↓↓ Ende

Ein Kurvenschreiber

Zusammenfassung

Vor etwa 30 Jahren entwarf ich ein Gerät, mit dem sich verschiedene mathematische Kurven schreiben lassen. Zu einer kommerziellen Anwendung ist es nicht gekommen. Ich besitze noch einen Prototyp, den ich hier zusammen mit damals angefertigten Texten und Bildern vorstellen möchte.

Inhalt

1. Kurzbeschreibung   ↑ Anfang

2. Das angewendete Prinzip   ↑ Anfang

Ebene mathematische Kurven werden in der x-y-Ebene dargestellt. Ein Stift (1), der sie zeichnen soll, hat sowohl eine Bewegung in Richtung der x-Achse als auch in Richtung der dazu senkrechten y-Achse auszuführen. Legt man zwei geschlitze Platten (2 und 3) 90° gegenseitig verdreht übereinander, so bleibt an der Kreuzungsstelle ein kleiner viereckiger Durchlass, in den man den Schreibstift stecken kann. Bei Bewegung der Platten (2) in x-Richtung und (3) in y-Richtung fährt der Durchlass über der darzustellenden Kurve y = f(x), die von dem Stift auf der Unterlage (4) an der Stelle (5) geschrieben wird.

Die beiden Platten (für Kurven y = y₁(x) + y₂(x) auch die Unterlage-Platte (Schreibplatte) (4)) werden von untereinander synchronisierten drehenden Rädern (9) und (10) angetrieben.

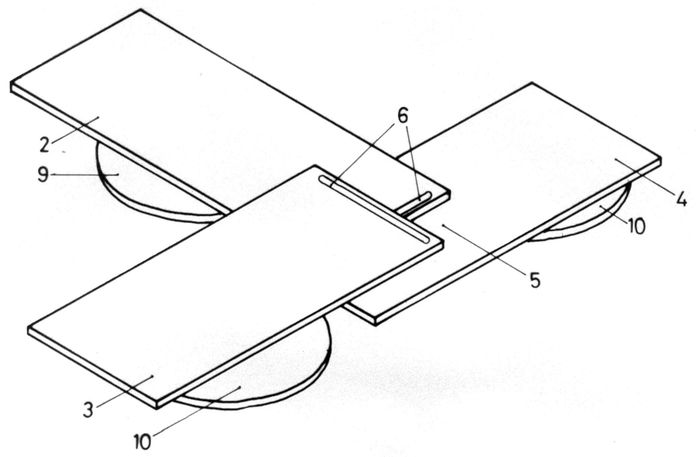
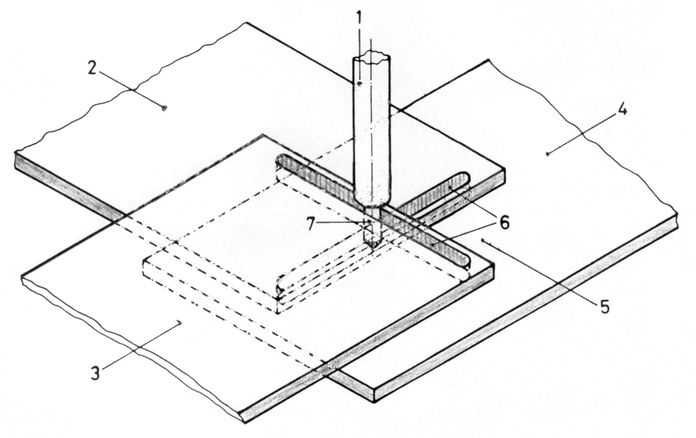
Abb.1 und Abb.2

3. Konstruktion (Prototyp)   ↑ Anfang

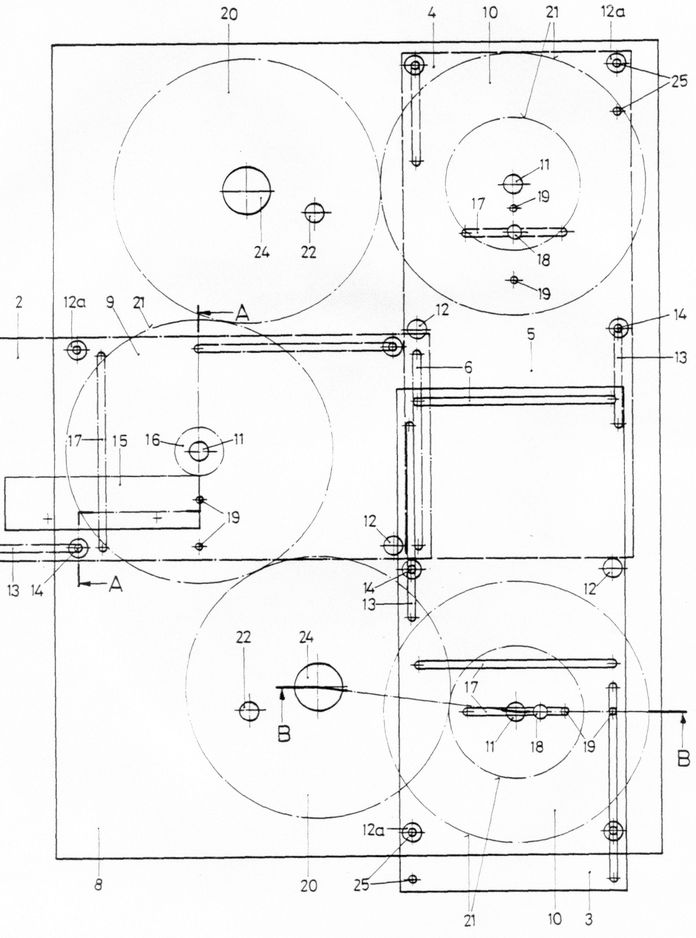
Abb.3

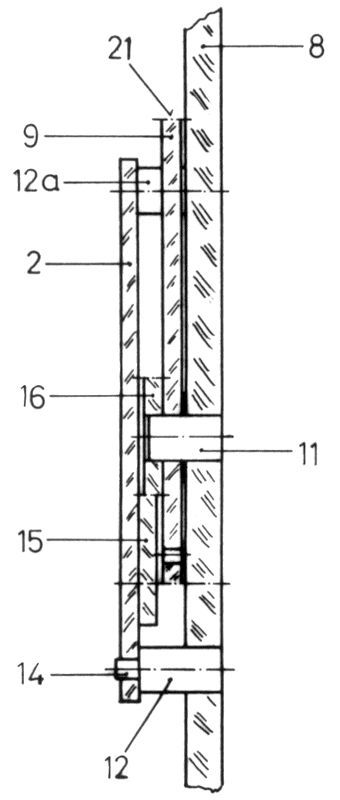
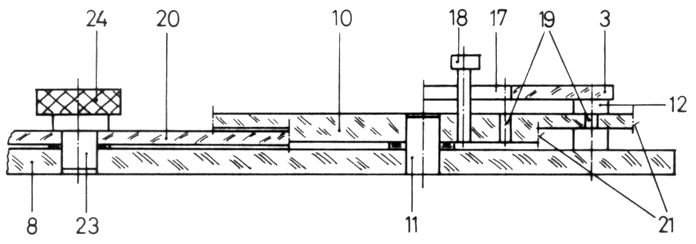
↑ ↑ Abb.4 Schnitt B-B in Abb.3 (vergrößert)
 ← Abb.5 Schnitt A-A in Abb.3 (vergrößert)

Die Grundplatte (8) ist 250 mm breit und 340 mm hoch. Sie passt in der Breite ganz und in der Höhe so auf das sichtbare, 250 mal 250 mm² große Arbeitsfeld eines Überkopfprojektors, dass auch in der Höhe die wesentlichen Teile des Kurvenschreibers projiziert werden können.

Der Kurvenschreiber ist zum Schreiben verschiedener Arten von Kurven geeignet, wofür er umrüstbar ist. In der Anordnung nach Abb.3 ist das fortschreitende Schreiben über der x-Achse möglich. Die x-Platte (2) ist mit einer Zahnstange (15) verbunden, mit der sie von einem Ritzel (16) angetrieben wird. Der Hand-Antrieb erfolgt am Knopf (24) eines der beiden Zahnräder (20), die das Zahnrad (9) drehen, auf dem das Ritzel (16) koaxial (11) befestigt ist.

Die über der x-Platte liegende y-Platte (3) und die unten liegende Schreibplatte (4) werden harmonisch auf- und abbewegt , was mit Hilfe je eines Kreuzschleifen-Getriebes erfolgt: Die Platten haben senkrecht zur Bewegungsrichtung einen Schlitz (17), in den ein auf dem darunter befindlichen Antriebs-Rad (10) befindlicher Stift (18) gleiten kann.

Die andere Haupt-Art von schreibbaren Kurven sind Lissajous-Figuren. Die Schreibplatte bleibt unbewegt. Die x-Platte wird auch mit einem Kreuzschleifen-Getriebe angetrieben und harmonisch hin- und herbewegt.

4. Sinus- und Cosinus-Kurven   ↑ Anfang

In der Anordnung nach Abb.3 werden Sinus- oder Cosinus-Kurven oder deren Summe (wenn die Schreibplatte auch angetrieben ist) geschrieben. Zur Variation der Amplitude wird der Stift (18) auf einem anderen Lochkreis (19) angebracht. Zur Variation der Phasenlage haben die Lochkreise mehrere über den Umfang verteilte Gewindelöcher zu Einschrauben des Stifts. Die Frequenz lässt sich im Verhältnis 1:2 verändern: Unter die y-Platte passt ein 2-stufiges Stirnzahnrad, dessen kleiner Kranz zur Frequenz-Verdopplung nach unten gekehrt wird. Das zwischen-Handrad wird in eine andere Lagerbohrung (22) gesteckt.

Die folgenden Bilder (Abb. 6 a, b, c) zeigen die detaillierte Anordnung zum Erzeugen der drei in der Kurzbeschreibung im Bild 1 gezeigten Kurven.

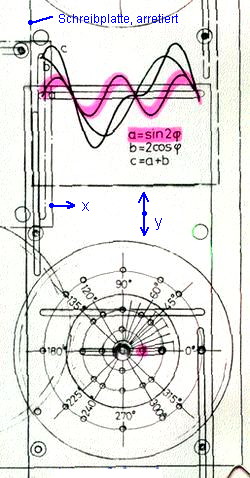
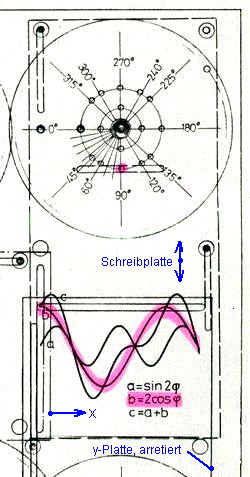
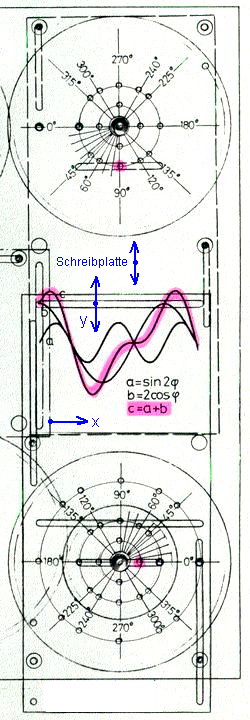Abb. 6 a, b, c

5. Lissajous-Figuren   ↑ Anfang

Die klassischen Lissajous-Figuren sind die Summe zweier zueinander rechtwinklig verlaufender harmonischer Bewegungen. Im Kurvenschreiber wird zu diesem Zweck auch die x-Platte mit Hilfe eines Kreuzschleifen-Getriebes hin- und herbewegt. Von der x-Platte ist die Zahnstange (15) abzuschrauben und mit Hilfe eines im Quer-Schlitz (17) gleitenden Stiftes (18) mit dem Rad (9) zu verbinden. Die Schreibplatte bleibt unbewegt, außer bei besonderen Figuren, die durch Überlagerung von drei harmonischen Bewegungen entstehen (Abb.9).

Die folgenden Bilder (Abb.7 und Abb.8) zeigen die detaillierte Anordnung zum Erzeugen der in der Kurzbeschreibung im Bild 2 und 3 gezeigten Lissajous-Figuren.

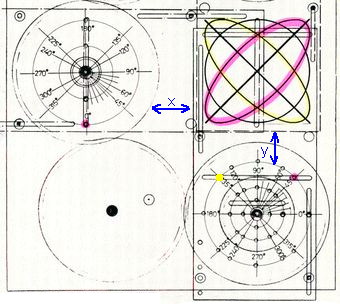
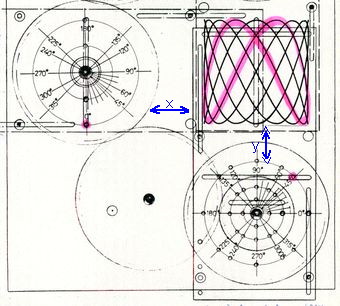
Abb.7, Abb.8

Zu Abbildung 7:
Beide Bewegungen haben die gleiche Frequenz (das antreibende Handrad kämmt mit gleich großen Rädern der beiden Kreuzschleifen-Getriebe) und die gleiche Amplitude (die schleifenden Stifte (18) sitzen auf den gleich großen äußeren Loch-kreisen (19)). Variable ist nur die Phasenverschiebung zwischen den beiden harmonischen Bewegungen. Bei 0° wurde der Kreis (schwarz) gezeichnet, bei 45° (rot) bzw. 135° (gelb) die beiden Ellipsen (rot und gelb). Zu den Geraden (schwarz) gehören die Verschiebungen 90° (G. nach rechts oben ) und 180° (G. nach links oben).

Zu Abbildung 8:
Die Bewegung der y-Platte hat gegenüber der x-Platte doppelte Frequenz (mit doppelten Pfeilspitzen bei y angedeutet, unter der y-Platte kämmt der kleinere Zahnkranz mit dem antreibenden Handrad). Beide Platten haben die gleiche Amplitude. Variable ist nur die Phasenverschiebung zwischen den beiden harmonischen Bewegungen. Bei 0° wurde die symmetrische, an eine Lemniskate erinnernde Doppelschleife (schwarz) mit zentrischem Knoten gezeichnet. Bei Phasenverschiebung wandert der Knoten zunächst nach oben, die Doppelschleife wird enger (45°, rot). Bei 90° ist sie zum einfachen, nach unten offenen Bogen geworden. Danach wandert der Knoten wieder nach unten: bei 135° ist die Figur gleich der bei 45° (rot), bei 180° gleich der bei 0°. Die weiteren Phasenverschiebungen bis 360°=0° entstehen die Figuren mit Knoten in der unteren Hälfte. Bei einem ganzen Umlauf des die x-Platte bewegenden Rades wird jede dieser Lissajous-Figuren 2 mal durchfahren.

Zu Abbildung 9:
Die Schreibplatte wird wie die x- und die y-Platte zusätzlich auch harmonisch bewegt. Dadurch entstehen "erweiterte" Lissajous-Figuren. Die Abbildung 9 enthält den Geräte-Aufbau, mit dem das in der Kurzbeschreibung verwendete Signet geschrieben wird. Die mittlere symmetrische Doppelschleife aus Abbildung 8 wird flacher bei gewähltem Amplitudenverhältnis 1:2 und vertikal verzerrt durch die vertikale Mitbewegung der Schreibfläche. Die zweite Doppelschleife des Signets entsteht bei umgekehrter Mitbewegung der Schreibfläche.

Abb.9 Gekoppelte und synchrone harmonische Bewegung der x-, der y- und der Schreib-Platte:
Normale Lissajous-Figuren werden verzerrt.
Einschraubstelle des Gleitstiftes (18) zur Schreibplatten-Bewegung passend zur Figur farblich markiert (im Bild oben).

6. Vektor-Additionen   ↑ Anfang

Man kann die einzelnen Hin- und Herbewegungen auch als Vektoren auffassen. Bei entsprechender Phasenlage der beiden geraden Spuren stoßen diese an ihren Enden zusammen und bilden ein rechtwinkliges Vektor-Paar. Werden die Bewegungen mit Frequenz-Verhältnis 1:1 gekoppelt, so wird der resultierende Vektor gezeichnet. In Abbildung 10 ist ein dafür brauchbarer Geräte-Aufbau gezeigt.

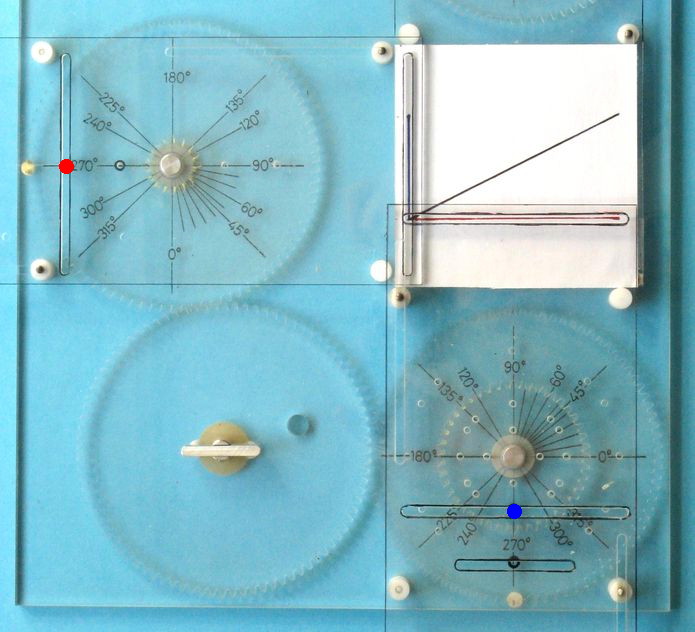
Abb.10 Vektor-Addition:
Die horizontale und die vertikale Linie entstehen bei Einzel-Bewegung der x- bzw. der y-Platte.
Sind beide Gleitstifte (18) (rot für x-, blau für y-Richtung) gesetzt, wird der resultierende Vektor (schwarz) geschrieben.

Bei Phasenlage, in der sich die Spuren in ihrer jeweiligen Mitte kreuzen, kann man auch Vektor-Additionen erkennen, wenn man nur die Hälften der Spuren betrachtet. So sind die beiden schrägen Linien in Abbildung 7 vier Vektoradditionen mit Anfang im Kreuzungspunkt. Jede von ihnen ist die Vektorsumme aus einem horizontalen und einem vertikalen Vektor (die Summanden sind nicht gezeichnet). Je ein Vektor-Tripel füllt einen der vier Quadranten der Schreibfläche.

Siegfried Wetzel, CH 3400 Burgdorf, März 2011 (Jan.20)

 ↑↑ Anfang
<< andere "Rechnen"-Beiträge
<< Home