<< Home
<< andere "Rechnen"-Beiträge
↓↓ Ende
Das Hilfsmaß Bel
Fürs Erste verweise ich auf den einschlägigen Artikel in der Enzyklopädie Wikipedia, dessen Einleitung ich schrieb. Ein paar eigene Bemerkungen zur Anwendung des Bel's bzw. des Dezibel's in der Akustik stelle ich hier vor. "Außer Konkurrenz" (weil gerade von Logarihmen die Rede ist) sind noch ein paar Erinnerungen an Rechnen mit Logarithmen aus meiner Schulzeit beigefügt.
Logarithmus eines Werte-Verhältnisses
Die Anwendung der Hilfsmaßeinheit Dezibel ist den meisten Lesern aus der Akustik bekannt. Um nicht mit Nachkommastellen des Messwertes umgehen zu müssen, wird ein mit Bel gekennzeichneter Wert verzehnfacht und mit Dezi-Bel gekennzeichnet: 1 Bel = 10 Dezi-Bel = 10 dB .
In der Akustik und in anderen physikalischen Bereichen arbeitet man oft nicht mit den Werten physikalischer Größen selbst, sondern mit dem Verhältnis zweier Werte einer dieser Größe. Ein solches Werteverhältnis ist dimensionslos. Die Angabe einer Dimension entfällt. Es liegt eine nackte Zahl vor. Man sagt auch, diese Zahl bzw. dieser Wert habe die Dimension Zahl. Als hifreicher hat sich allerdings erwiesen, Werteverhältnisse mit einer Hilfsmaßeinheit zu kennzeichnen. Der Wortteil Hilfs- deutet in diesem Falle daraufhin, dass er unnötig ist - z.B. für Berechnungen - und nur eine kennzeichnende Hilfsfunktion hat. Bel (bzw. dB) ist eine dieser Hilfsmaßeinheiten, eine andere ist Neper.
Bel und Neper unterscheiden sich darin, welcher Logarithmus von der Zahl des Werteverhältnisses gebildet wird. Weil sich die Werte und damit auch die Werte-Verhältnisse mancher physikalischer Größen mit ihrer Wirkung nicht linear ändern (meistens beim Anwachsen), verwendet man nämlich den Logarithmus der Verhältnisse.
Mit dem Bel (und dem dB) wird der dekadische Logarithmus eines Verhälnisses gekennzeichet. Auf einer Skala sind die Schritte für die Verhältnisse ... 0,1 bis 1, 1 bis 10, 10 bis 100, 100 bis 1000, ... alle gleich groß.
Mit dem Neper wird der natürliche Logarithmus eines Werte-Verhälnisses gekennzeichet.
Das Dezibel in der Akustik
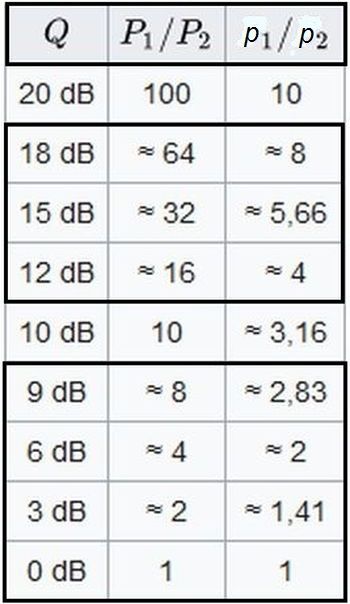
In der praktischen Akustik geht es häufig darum, die Lärmbelastung an einem Ort oder von einer bestimmten Schallquelle stammend, zu bestimmen. Umgangssprachlich spricht man auch von der Lautstärke. Mit beiden ist die physikalisch-technische Größe Schallleistung P gemeint.
Der Wert P1 der zu bestimmenden Schallleistung wird durch den Wert P2 einer Bezugsleistung geteilt und davon der dekadische Logarithmus gebildet. Das Zehnfache der so gefundenen Zahl ist der in dB anzugegebende Schallleistungspegel Q . In der Akustik hat man P2 = 10-12 Watt = P0 als Wert der Bezugsleistung festgelegt.
Die Schallleistung wird nicht direkt gemessen, sondern aus dem gemessenen Schalldruck p berechnet. Da die Schallleistung zum Quadrat des Schalldruckes proportional ist, gilt: P1/P2 = (p1/p2)2
Anstatt vom Schalleistungspegel wird auch verkürzt vom Schallpegel gesprochen. Ein anderer verwendeter Begriff ist irreführemd Schalldruckpegel. Korrekt wäre Quadrat des Schalldruckpegels, denn der Schaldruckpegel ist p1/p2 . Dessen vereinbarter Bezugsdruck ist p2 = 10-5 μPa = p0 . (Pa = Pascal)
Man erkennt bei dieser Gelegenheit, wie klein die absoluten Werte des Schalls sind: Bei der mittleren Lautstärke
60 dB beträgt der Schalldruck nur 10-2 μPa und die Schalleistung nur 10-6 Watt.
Eine bekannte Äußerung bei Gesprächen über Lärmbelastung ist, dass sich die Lautstärke verdoppelt wenn der Schallpegel um etwa 3 dB wächst (oder umgekehrte Reihenfolge oder umgekehrt bei Sinken des Pegels). In der beigefügten Tabelle ist das beim Vergleich der beiden ersten Spalten erkennbar. Dass das so sein muss, ist klar, wenn man den schon in der Schule "gepaukten" dekadischen Logarithmus 0,3010 für 2 behalten hat (0,301 Bel = 3,01 dB). Die rechte Spalte enthält das Schalldruck-Verhältnis, also jeweils die Wurzelwerte der Werte in der zweiten Spalte.
Rechnen mit Logarithmen
In einem Rahmen links sind die einfachen Rechenarten genannt, die man üblicherweise in der Schule mit Hilfe von Logarithmen anzuwenden erlernte und übte. Das geschieht offensichtlich seit der Einführung des elektronischen Taschenrechners nicht mehr. Vorher gehörte zu den persönlichen Lehrmitteln eine Logarithmen-Tabelle. Meistens besaß man das Heftchen Schülkes Tafeln, das ganz vorne eine zweiseitige Tafel mit 4-stelligen Logarithmen für die Zahlen 10 bis 999 hatte. Damit addierte und multiplizierte man Logarithmen-Werte von Hand. In der Industrie hatte man immerhin damals mechanische Rechenmaschinen, mit denen man das Addieren und Multiplizieren machen konnte, z.B. in den Büros der optischen Industrie, wo ich 1958 ein Praktikum während des Ingenieur-Studiums absolvierte, zur Berechnung von Linsen (wobei hier meistens der Logarihmus trigonometrischer Winkelwerte gebildet wird).
Die Anwendung des analogen, in der Auflösung begrenzten Rechnens mit Logarithmen im Rechenschieber lernte ich erst nach der Schulzeit kennen, als mir mein Vater erlaubte, seinen Rechenschieber zu benutzen. In meiner Schulzeit bis 1955 besaßen Schule und Lehrer keinen einzigen Rechenschieber.
Beim Rechnen mit Logarithmen werden die Grundrechenarten mit der jeweils tieferen Rechenart ausgeführt.
Die Multiplikation der Zahlen a · b erfolgt als Addition ihrer Logarithmen: log (a) + log (b) = log (c) .
Das Ergebnis c erhält man, indem man auf die Summe der Logarithmen die Umkehrfunktion zum Logarithmieren anwendet.
Im folgenden Bild (Quelle: Wikipedia) eines auf zwei Skalen reduzierten Rechenschiebers ist die Multiplikation
2 · 3 = 6 dargestellt. Sie erfolgt als Addition log (2) + log (3) = log (6) . Die Umkehrfunktion zum Logarithmieren ist wie das Darstellen der Logarithmen der Faktoren als Strecken durch die Skalierung des Rechenschiebers vorgegeben. Man kann das Ergebnis 6 direkt ablesen. Ausführungsschritte: 1 über 2 stellen und unter der 3 die 6 ablesen.
Die abgebildete Schieberstellung zeigt auch die Division 6 : 3 = 2 (und 6 : 2 = 3 ) . Ausführungsschritte: 3 über 6 stellen und unter der 1 die 2 ablesen (1 über 2 stellen und über der 6 die 3 ablesen).
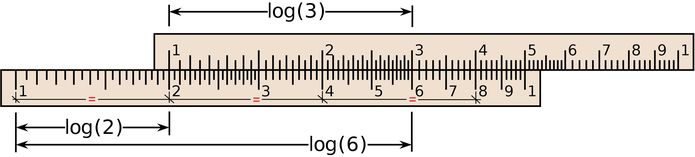
Im Rechenschieber-Bild sind auf dem unteren Schieber die Strecken 1-2, 2-4, und 4-8 zuätzlich markiert, um auf die logarithmische Skalierung hinzuweisen. Sie sind alle gleich lang, obwohl sie fortgesetzt für eine jeweils verdoppelte Zahlendiverenz gelten.
Das Potenzieren erfolgt als Multiplikation log (a) · b = log(c) ,
das Wurzelziehen a-b als Division log (a) : b = log(c) .
Mit einem Rechenschieber sind faktische Multiplikationen und Divisionen nicht möglich. Man hat ihm aber oft mit einem Nomogramm für den Exponent b = 2 , manchmal zusätzlich noch mit einem Nomogramm für den Exponent b = 3 ergänzt. Im ersten Fall wird der festen Skala 1 bis 10 eine zweite Skala mit zwei je auf die halbe Länge gestauchten Hälften 1 bis 10 und 10 bis 100 fix zugeordnet. Im zweiten Fall hat die zugeordnete Skala drei gestauchte Drittel 1 bis 10 , 10 bis 100 und 100 bis 1000 . Auf dem Rechenschieber im folgenden Bild (Schiebeteil aus Mitte entfernt) sind beide genannten Nomogramme vorhanden. Die drei verschiedenen Skalenteilungen sind im Bild farblich markiert.
Im nächsten Bild ist der rechte Teil dieses Rechenschiebers gezeigt (Schiebeteil aus Mitte entfernt). Eingestellt sind mithilfe des Strichmarken-Schiebers
82 = 64 und 83 = 512 bzw. 64½ = 8 und 512⅓ = 8 . Die drei Zahlen sind im Bild vergrößert markiert.
Siegfried Wetzel, CH 3400 Burgdorf, Mai 2021
↑↑ Anfang
<< Home
<< andere "Rechnen"-Beiträge
