<< Home
<< andere "Rechnen"-Beiträge
 ↓↓ Ende

Zahlenschieber

Zusammenfassung

Der Zahlenschieber (auch:Addiator®) war ein einfaches Gerät für Additionen und Subtraktionen. Er wurde durch den für Multiplikation und Division geeigneten Rechenschieber ergänzt. Die Rechnungen mit dem Zahlenschieber wurden Schritt für Schritt in jeder Zehnerstelle einzeln durch Verschieben je eines zugehörenden Zahlenstabes ausgeführt (nur 1 erster (engl: Augend) und 1 zweiter Summand (engl: Addend) pro Schritt beziehungsweise nur 1 Minuend und 1 Subtrahend pro Schritt). Die Benutzung kann heute noch zugänglichen Gebrauchsanweisungen entnommen werden [1]. Weniger bekannt ist aber, wie es im Inneren eines Zahlenschiebers aussieht [2], beziehungsweise wie dessen Erfinder und Hersteller das bis anhin zählende Rechnen mittels Akabus oder Zahlenbrett (Rechnen auf Linien) oder das Rechnen auf Papier oder im Kopf in dieses einfache anzeigende technische Gerät übertrugen. Der vorliegende Artikel beschreibt einige diesbezügliche Zusammenhänge.

Inhalt

1. Grundlagen   ↑ Anfang

Eine Addition und eine Subtraktion lassen sich auf das Verschieben eines Zahlenstabes übertragen, und das Ergebnis ist an dessen eingenommener Lage erkennbar. Diese beiden Grundrechenarten sind gegenseitige Umkehroperationen. Somit entspricht das Hinschieben des Stabes der einen und sein Zurückschieben der anderen Operation. Beim Rechnen im dezimalen Stellenwertsystem wird für jede Stelle ein Zahlenstab mit den Ziffern 0 bis 9 verwendet.

1.1 Schieben eines einzelnen Zahlenstabes   ↑ Anfang

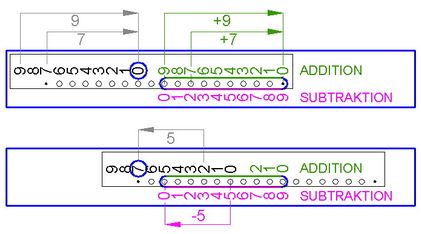
Abb.1
Verschieben eines für eine dezimale Stelle gebrauchten Zahlenstabs.
oben:  "hin" (nach rechts) = Addition,
          Beispiele: 0+7 und 0+9.
unten: "zurück" (nach links) = Subtraktion,
          Beispiel: 7-5=2,
          erst nach vorheriger Addition möglich.

Es gibt Zahlenschieber, die wie in Abb.1 sowohl für die Addition als auch für die Subtraktion vom gleichen Gehäuseschlitz aus bedient werden. Die dafür bei der Eingabe des Addenden bzw. des Subtrahenden gebrauchten Skalen wachsen in gegensätzlichen Richtungen, was bei nicht genügender Aufmerksamkeit zu Fehlern durch Verwechslung der beiden führt. Man weicht deshalb auf Lösungen mit zwei voneinander getrennten Schlitzen mit je nur einer Skala aus. Die historisch ältere Lösung ist deren Anordnung in Reihe zueinander (Abb.2). Das Ergebnisfenster bei solchen relativ langen Zahlenschiebern befindet sich meistens zwischen den beiden Bedienfeldern, was deren Trennung zusätzlich betont.

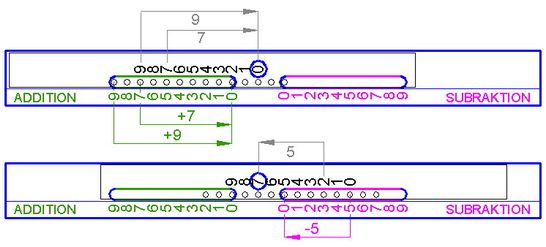
Abb.2
In Reihe angeordnete Bedienskalen für einen Zahlenstab (2 Schlitze).
Rechenbeispiele wie in Abb.1.

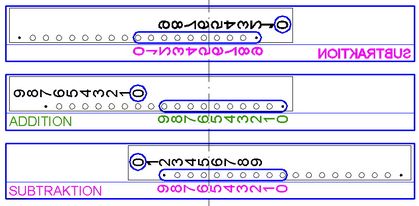Abb.3
Vorder- (Mitte) und Rückseite (unten) des Zahlenschiebers aus Abb.1 mit beidseits angeordneten Bedienskalen und -schlitzen.
Zahlenstab auch beidseitig beschriftet.
Oben: Blick von vorn auf rückseitige Beschriftungen des durchsichtig gedachten Stabs und des durchsichtig gedachten Gehäusebodens.
Unten: nach Seitenwechsel durch Wenden um eine im Bild vertikale Achse.
Gleiche Länge wie in Abb.1

1918 wurde die doppelseitige Bedienung des Zahlenschiebers vom Berliner Otto Meuter erfunden, durch deren Anwendung die Marke Addiator® erfolgreich wurde [3]. Der Addiator® ist so kurz wie prinzipiell möglich und lässt sich durch die Verteilung der Zugriffe auf beide Gehäuseseiten verwechslungsfrei bedienen (Abb.3 und Abb.5).

1.2 Übertragen auf den zweiten Stab   ↑ Anfang

Das Zusammenzählen von zwei mehrstelligen Zahlen auf Papier geschiehtt infolge der anzuwendenden Regeln zum Beispiel mit folgendem Kommentar; die Summe sei 17 + 16:

• 7 + 6 ergibt 13; schreibe 3, merke 1
• 1 + 1 + gemerkt 1 ergibt 3; schreibe 3

Der Übertrag machte den Erfindern von Rechenhilfen stets Schwierigkeiten. Nach einer oft zitierten Klassifikation entsteht mit dem Übertrag erst eine Rechenmaschine [4]. Beim Zahlenschieber ist das ähnlich. Er ist zwar noch keine Rechenmaschine, erlangte aber seine Vollkommenheit durch Zufügen des Zehnerübertrags, der sich beim Schieben von Hand zwangsläufig ergiebt. Der sogenannte Hakenübertrag wurde 1847 vom deutschen Musiklehrer Heinrich Kummer erfunden [5]. In Abb.4 ist die Durchführung des Zehnerübertrags zwischen zwei dekatischen Stellen bei Addition dargestellt. Zum Bedienen haben die Zahlenstäbe an beiden Rändern zahnstangenartige Lücken zur Mitnahme mittels eines Griffels. Die Gehäuseschlitze sind 10 Einheiten lang und an einem Ende hakenförmig gestaltet.

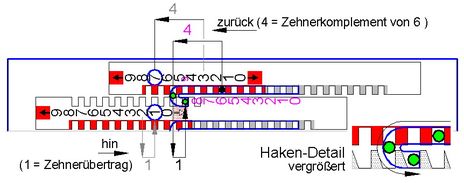Abb.4
Zehnerübertrag; Beispiel 17 + 6 (= 23)

In der "überlaufenden" Einer-Stelle ist das Ergebnis im obigen Beispiel 3. Die 3 ist auch das Ergebnis aus 7 - 4 (Augend -4). 4 ist das Zehnerkomplement von 6 (dem Addenten). Diese faktische Subtraktion einer 4 in der Einer-Stelle wird automatisch erreicht durch Schieben des Zahlenstabs von der 6 der gerätefesten Skala aus in Gegenrichtung ( "zurück" trotz Addition). Nach Verschieben um 4 Einheiten ist der Anschlag erreicht, und im Fenster erscheint die 3 als Ergebnis.

Dieser Anschlag ist keine Querwand wie der "normale" Anschlag am anderen Ende des Bedienschlitzes. Er ist als Hakenkurve ausgeführt, durch der Bedien-Griffel umgelenkt und parallel wieder ein kleines Stück zurück geführt wird. Dem Bediener wird diese Bewegung als quasi harmonische abgenötigt. Der Griffel rastet im Kurvenscheitel vom Einer-Stab aus und beim Zehner-Stab ein. Er erreicht nach einer Strecke mit der Einheit 1 nach dem Kurvenscheitel seinen endgültigen Anschlag. Bis dahin hat er den Zehner-Stab 1 Einheit mitgenommen und dessen Anzeige um 1 erhöht (im Beispiel von 1 auf 2).

Die in der Zehnerstelle auszuführende Beispiel-Addition 1 + 1 ist ohne Besonderheiten. Der Zehner-Stab wird 1 Einheit an den "normalen" Griffel-Anschlag herangezogen. Dabei erhöht sich der von ihm angezeigte Wert von inzwischen 2 auf 3.

Bei der Subtraktion wird der Zehnerübertrag prinzipiell gleich vorgenommen mit dem Unterschied, dass beim Führen des Griffels zur Haarnadelkurve der Wert in der Einer-Stelle vergrößert und beim Führen aus der Kurve heraus der Wert in der Zehner-Stelle um 1 verkleinert wird.

In Abb.4 sind die Zahlenstäbe im Unterschied zu den schematischen Darstellungen in den Abbildungen 1 bis 3 nicht nur mit 10 Ansatzpunkten (Zahnlücken), sondern mit der doppelten Zahl versehen. Sie müssen bei anliegendem Zehnerübertrag auch "zurück" geschoben werden können, wofür von einem Bedienfenster aus insgesamt 20 zugreifbare Zahnlücken nötig sind. Die zusätzlichen Zahnlücken sind anders gekennzeichnet als die Lücken 1 bis 10 (in der Abb. rot gegenüber grau). Bei einem Zehnerübertrag greift der Griffel in eine dieser Zusatzlücken, deren andere Kennzeichnung auf die andere Schieberichtung hinweist.

Wenn die Anzeige in der Zehner-Stelle bereits 9 (für 90) ist, funktioniert der nötige doppelte Übertrag von der Einer-Stelle aus über die die Zehner- weiter in die Hunderter-Stelle nicht. Es ist dann ein zweiter Schritt nötig, der keineswegs quasi beiläufig wie der erste erfolgt. Der Zehner-Stab hat durch den Übertrag vom Einer-Stab aus seinen Anzeigebereich über 9 hinaus verlassen, was beispielsweise durch einen angezeigten roten Fleck signalisiert wird. Er muss um 10 Einheiten "zurück" geschoben werden, damit seine am Anfang stehende 0 unter dem Fenster erscheint. Der Griffel muss bei der O der Gehäuseskala eingesteckt und bis zum anderen Schlitzende und durch die Haarnadelkurve geführt werden. Bei der kurzen Fahrt nach der Kurve wird eine 1 in der Hunderter-Stelle addiert (siehe folgenden Abschnitt: 2. Beispiel-Additionen mit dem Zahlenschieber, Abb.11).

Abb.5 Zweiseitiger Zahlenschieber: interaktive virtuelle Nachbildung des Addiator Duplex ®
          (Gehäuse leicht durchsichtig).
          Beim Seitenwechsel wird das Gerät nicht wie eine Buchseite, sondern wie ein Kalenderblatt um eine
          horizontale Achse gewendet.
          Das Subtrahieren scheint sich nicht vom Addieren zu unterscheiden. Der Wechsel vom "hin" zum "zurück" liegt
          aber vor, denn die Zahlenreihen auf den gewendeten Zahlenstäben (Subtraktion) steigen in entgegengesetzte
          Richtung gegenüber denen auf den ungewendeten Stäben (Addition) an [6].

2. Beispiel-Additionen mit dem Zahlenschieber  ↑ Anfang

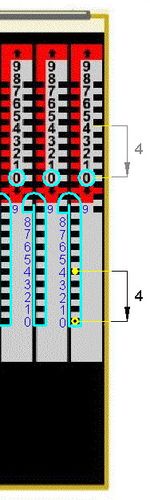
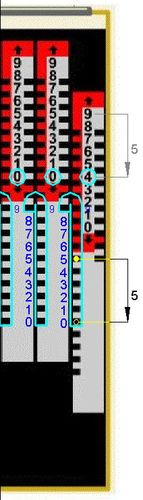
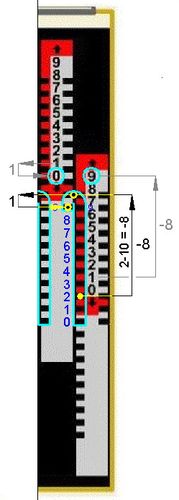
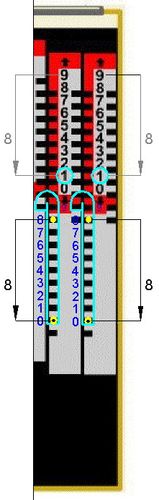
 Abb.6   0+4                        Abb.7   4+5                       Abb.8   9+2                                Abb.9   11+88

Zuerst wird in der Einer-Stelle addiert: 0+4=4 (Abb.6) und 4+5=9 (Abb.7).

Mit dem Zwischenergebnis 9 ist die Einer-Stelle gänzlich gefüllt. Jede folgende Addition führt zu einem Zehnerübertrag. Ein Hinweis darauf ist, dass der Griffel nur noch in rot umrandete Zahnlücken des Einer-Stabes gesteckt werden kann (Abb.8). Der Stab ist nun in Gegenrichtung (zurück nach oben) zu schieben, wobei der Griffel bei seiner Fahrt durch den Schlitzhaken in eine Zahnlücke am rechten Rand des links liegenden Zehner-Stabes wechselt und diesen 1 Einheit vorwärts nach unten zieht, d.h. den Zehnerübertrag durchführt.

Auf seinem vorherigen Weg zwischen dem Einstich bei der zu addierenden 2 (Abb. 8) und dem Hakenscheitel verringert er die Anzeige des Einerstabes um 8 Einheiten auf 1 (9 + (2-10) =1; der Weg nach oben ist als negative Zahl angeschrieben: -8). Das Zwischenergebnis nach der dritten Rechnung (9+2=11) ist in Abb.9 zu sehen.

Zur Vorbereitung auf einen doppelten Zehnerübertrag von der Einer- über die Zehner- in die Hunderter-Stelle wird die Rechnung 11+88=99 ausgeführt (Abb. 9 und Abb.10). Diese Rechnung ist ohne Besonderheiten: In beiden Stellen wird der Stab vorwärts nach unten gezogen. Nicht nur hier spielt es keine Rolle, in welcher Stelle zuerst gerechnet wird. Das bezieht sich auf alle Additionen und Subtraktionen. Die vorliegenden Beschreibungen sind lediglich in Analogie zum schriftlichen Rechnen von rechts nach links fortschreitend vorgenommen.

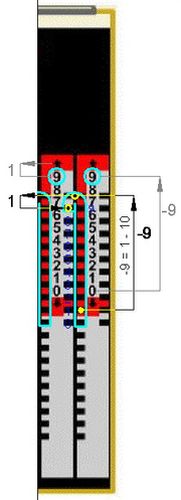
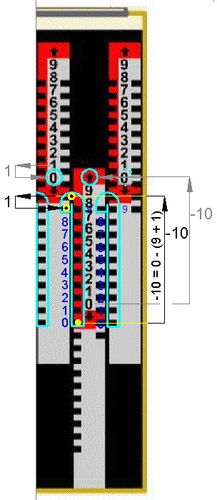
                 Abb.10   99+1                             Abb.11 Aufforderg. f. Zehnerübertrag      Abb.12   99+1=100

In der Stellung der beiden Stäbe auf 99 ist an ihren rot umrandeten Zahnlücken zu erkennen, dass jede weitere Addition in beiden Stellen einen Zehnerübertrag zur Folge hat (Abb.10). Es folgt die Addition 99+1=100.

Das Rückverschieben (nach oben) des Einer-Stabes um 9 Einheiten (-9=1-10) bewirkt, dass er 0 anzeigt. Bei der Fahrt aus der Hakenkurve führt der Griffel den Zehnerübertrag aus. Der Zehner-Stab bewegt sich auf eine Stelle oberhalb der 9 und zeigt einen nach oben weisenden Pfeil auf rotem Grund anstatt der 0 an (Abb.11). Er musss in einem zusätzlichen Schritt um 10 Einheiten nach oben geführt werden, was der bei Gehäuse-0 eingesteckte und nach oben zum Haken geführte Griffel bewirkt. Bei Hakenausfahrt erfolgt der Zehnerübertrag zum Hunderter-Stab. Das Ergebnis ist 100 (Abb.12).

Der in Abb.11 angezeigte Pfeil auf rotem Grund diente als Hinweis dafür, dass ein besonderer Bedienschritt nötig war. In der Regel werden die Skalen auf den Stäben immer an beiden Enden mit solchen Pfeilen versehen als allgemeiner Hinweis darauf, dass der Anzeigebereich durch eine Fehlbedienung verlassen wurde. Würde zum Beispiel in Abb.6 der Stab versehentlich nach oben anstatt nach unten bewegt, würde im Ergebnisfenster ein nach unten, d.h. in die richtige Richtung weisender Pfeil erscheinen. In Abb.8 wäre es umgekehrt: nach oben weisender Pfeil, wenn versehentlich nach unten bewegt wurde.

3. Rechnen mit negativem Ergebnis   ↑ Anfang

Die meisten Zahlenschieber sind nicht für das Rechnen mit negativem Zwischen- oder Schluss-Ergebnis vorgesehen. Diese Aufgabe erfordert einen relativ geringen zusätzlichen Aufwand. Ein entsprechendes Gerät ist äußerlich an der zusätzlichen Fensterzeile erkennbar, in der der negative Saldo ("rote Zahlen") angezeigt wird [2].

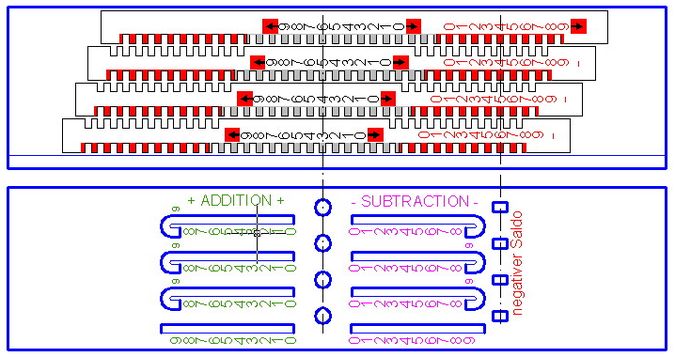Abb.13 Zahlenschieber mit in Reihe angeordneten Bedienskalen und zusäzlicher Anzeige negativen Saldos
            oben: Gehäuseboden mit Zahlenstäben
            unten: Gehäusedeckel mit Bedienschlitzen und Fensterzeilen

In Abb.13 ist ein solcher Zahlenschieber schematisch dargestellt. Er ist aus Abb.2 entwickelt (mehrere Zahlenstäbe für mehrere dezimale Stellen, Zahlenstäbe verlängert und an den Rändern verzahnt: zwei farbig unterschiedliche Abschnitte, wie in Abb.4). Außer der Verlängerung der Stäbe für getrennte Bedienung bei Addition und Subtraktion ist deren zusätzliche, in roter Farbe gedruckte Zahlenreihe auffällig.

Die mehrstelligen Zahlen in den beiden Fensterreihen - oben schwarze Zahlen , unten rote Zahlen - sind zueinander komplementär. Der Unterschied der einen Zahl zur Einheit in der nächst höheren, nicht besetzten Stelle ist die zu ihr komplementäre Zahl, z.B. 3'456 ist die Komplementäzahl zu 6'544 (s. Abb.13: 10'000 - 3'456 = 6'544) In jeder Dezimalstelle ist die Summe der in den beiden Fenstern sichtbaren Zahlen 9, außer in der letzten, der Einer-Stelle, wo die Summe 10 ist. Die rote Zahlenreihe auf dem letzten Zahlenstab befindet sich deshalb um 1 Einheit höher (weiter links in Abb.13) als die jeweilige auf den anderen Stäben.

Wenn eine Subtraktion zu einem negativen Ergebnis führt, erscheint in der vor der in der Rechnung nicht benutzten Stelle im Hauptfenster ein nach unten (und in Richtung zum Fenster für negativen Saldo) weisender Pfeil. Dies ist ein Hinweis dafür, dass die Rechnung zu einer "roten Zahl" geführt hat. Hinter dem Pfeil steht aber die Komplementärzahl zum negativen Ergebnis, das man notfalls im Kopf oder mit Stift auf Papier ermitteln kann, wenn man nur einen Zahlenschieber ohne zusätzliche Anzeige des negativen Saldos zur Verfügung hat.

Zahlenschieber mit zusätzlicher Anzeige des negativen Saldos erfordern im allgemeinen Fall lediglich, dem Hinweis auf das negative Ergebnis zu folgen und dieses im entsprechenden zusätzlichen Fenster abzulesen. Steht aber im oberen Fenster in der letzten Stelle eine 0, so ist eine Zusatzmaßnahme erforderlich, bevor der negative Saldo richtig ablesbar ist. Ursache ist, dass die 0 keine Komplementärzahl hat. Im Fenster für den negativen Saldo steht an letzter Stelle vorerst ein entsprechender Hinweispfeil. Er fordert auf, in der letzten Stelle die gleiche Zusatzmassnahme zu ergreifen, wie beim gewöhnlichen doppelten Zehnerübertrag (Abb.11 und 15).

Das Rechnen muss nicht beendet werden, wenn das Ergebnis zwischendurch negativ ist. Wenn es beim weiteren Rechnen wieder positiv wird, verschwindet der Hinweispfeil oben links. Man kann aber nicht einfach weiter rechnen, wenn die zum unteren Ablesen nötige Zusatzmaßnahme ergriffen wurde.

4. Beispiel-Subtraktionen mit dem Zahlenschieber   ↑ Anfang

Einleitend behandle ich eine Subtraktion mit doppeltem Zehnerübertrag analog zum Additions-Beispiel 99+1 (s. Abbildungen 9 bis 11). Anschließend zeige ich Subtraktionen mit negativem Saldo.

4.1 Subtraktion mit doppeltem Zehnerübertrag  ↑ Anfang

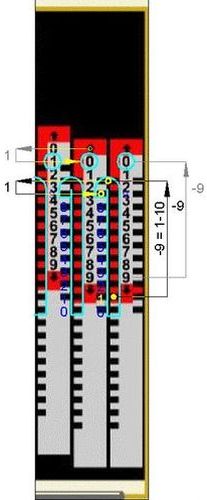
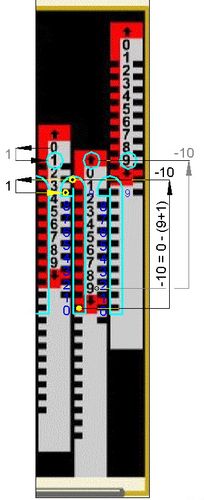
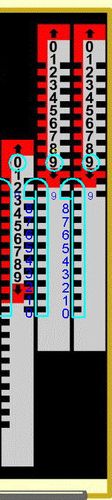
                 Abb.14   100-1                                 Abb.15 Aufforderg. f. Zehnerübertrag    Abb.16   100-1=099

Für die Rechnung in Abb. 14 bis 16 verwende ich wieder den zitierten [6] interaktiven Addiator ohne Gehäusedeckel ("100% Transparenz"), diesmal seine Subtraktions-Seite. Abb.15 betrifft den zusätzlichen Schritt für den doppelten Zehnerübertrag (entspricht Abb.11 bei Addition). Der Verschiebeweg in Richtung des Schlitzhakens wird auch hier mit negativem Vorzeichen angeschrieben. Damit ist generell die Gegenrichtung gemeint, die sowohl bei Addition als auch bei Subtraktion zu wählen ist, wenn ein Zehnerübertrag folgt.

4.2 Subtraktion mit negativem Saldo  ↑ Anfang

Dem interaktiven Zahlenschieber [6] fehlt die Anzeige eines negativen Saldos. Ich stelle zwei Beispielrechnungen dennoch mit dessen Hilfe dar. Die dort fehlenden roten Zahlenreihen auf den Stäben und die Fensterreihe für den negativen Saldo habe ich noch zusätzlich in bearbeiteten screen shots untergebracht. Beim Vergleich mit dem in Abb.13 gezeigten einseitigen Zahlenschieber ist die Richtungsumkehr in den Zahlenreihen und den Bewegungen bei der Bedienung zu beachten, denn beim interaktiven Zahlenschieber wird zur Subtraktion die entsprechend eingerichtete Rückseite (s.Abb.3) benutzt.

Anmerkung zu den Abbildungen 17 bis 20:
Im Unterschied zu allen obigen Abbildungen mit eingezeichneten Verschiebepfeilen befinden sich die Zahlenstäbe hier bereits in der verschobenen Stellung.

1. Beispiel: Abb.17 und 18
Die Rechnung 345 - 517 = -172 erfordert keine Zusatzmaßnahme. Sie ist wie im Beispiel in 4.1 auszuführen. Im Hauptfenster steht ↑828 (der Hinweispfeil und die Komplementärzahl zu 172), und in der unteren Fensterzeile steht -172, das Ergebnis der Rechnung einschließlich negativem Vorzeichen.

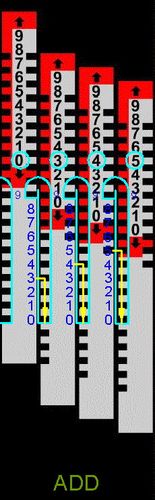
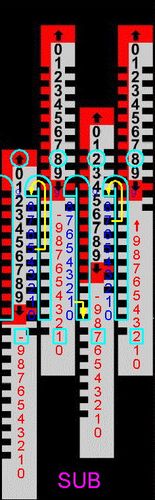
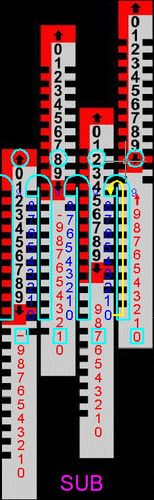
 Abb.17   0+345 = 345           Abb.18   345-517= -172         Abb.19   345-515 = ??          Abb.20   345-515= -170

2. Beispiel: Abb.19 und 20
345 - 515 = -170
Oben stehendes Ergebnis ist jetzt ↑830, und unten steht zunächst -16↑ (Abb.19). Wegen der 0 in der letzten Stelle ist die genannte Zusatzmaßnahme nötig, die gleich ist wie beim gewöhnlichen doppelten Zehnerübertrag (Abb.11 und 15). Der Stab wird von der Skalen-0 aus heraufgezogen, wonach im unteren Fenster die 0 angezeigt und durch die Hakenfahrt die Anzeige links daneben 1 Einheit erhöht ist. Ergebnis: -170, also jetzt vollständig und richtig.
Bei zwei oder mehr Nullen am Ende ist die Zusatzmassnahme zwei bzw. mehrmals erforderlich.

Das Rechnen muss nicht beendet werden, wenn das Ergebnis zwischendurch negativ ist. Wenn es beim weiteren Rechnen wieder positiv wird, verschwindet der Hinweispfeil oben links. Man kann aber nicht einfach weiter rechnen, wenn die zum unteren Ablesen nötige Zusatzmaßnahme wie im 2. Beispiel ergriffen wurde.)* Die rot unterlegte letzte (bzw. mehrere letzte) obere Fensteröffnung macht darauf aufmerksam (Abb.20: falsch ↑82↓ anstatt richtig ↑830).

)* Zum Weiterrechnen muss diese Massnahme auf der ADDITIONs-Seite in der/n letzten Stelle/n in analoger Weise rückgängig gemacht werden.

5. Weblinks und Bild-Nachweise   ↑ Anfang

Siegfried Wetzel, CH 3400 Burgdorf, Dezember 2012 (Febr.13, Jan.20)

 ↑↑ Anfang
<< andere "Rechnen"-Beiträge
<< Home