<< Home
<< andere Mechanik-Beiträge
↓↓ Ende
Die Einflusslinie
- ein Arbeitsmittel bei Festigkeits- und Verformungsuntersuchungen in der Baustatik
Inhalt
1. Einleitung2. Definitionen
2.1 erstes Zitat
2.2 zweites Zitat
3. Beispiele
3.1 die Zustandslinie
3.2 die Einflusslinie
4. Schlussbemerkungen
5. Quellen
1. Einleitung
Die meisten Ingenieure benötigen die Einflusslinie als Arbeitsmittel beim Lösen ihrer mechanisch-statischen Probleme gar nicht. Deshalb kommt sie in den von ihnen gehörten Vorlesungen oft auch nicht vor. Im Maschinenbau gilt das fast ausschließlich. Weder im Studium, noch im Beruf (Konstruktion, Forschung und Lehre) hörte ich davon. Selbst der häufigere Begriff Zustandslinie war für uns nicht selbstverständlich. Staattdessen sprachen wir einfach von der Momenten-, der Normalkraft- und der Querkraftlinie. Aber im Bauwesen gibt es den Vollzeitberuf Statiker, und damit verbunden eine Reihe von besonderen Vorgehensweisen inkl. besonderen Begriffen. Dort ist die Einflusslinie inkl. ihrer Anwendungen sogar Gegenstand der DIN-Normen.Im Folgenden spreche ich über das Grundsätzliche der Einflusslinie. Über Ausführliches, d.h. wann ist ihre Anwendung besonders nützlich, wie breit ist das Anwendungsgebiet (Grundform des Tragwerks, statisch bestimmtes bzw. unbestimmtes Tragwerk, direkt bzw. indirekt belastetes Tragwerk, Einflusslinie nicht nur für Kraft- sondern auch für Weggrößen usw.) kann und will ich mich nicht äußern.
2. Definitionen
2.1 erstes Zitat [1]
Eine Einflusslinie unterscheidet sich wesentlich von einer Zustandslinie.Die Zustandslinie gibt die Werte einer bestimmten Zustandsgröße, z.B. eines Biegemoments, in allen Systempunkten infolge einer vorgegebenen ortfesten Beanspruchung an.
Die Einflusslinie dagegen beschreibt den Einfluss einer Einheitslast mit variablem Angriffspunkt auf eine Zustandsgröße an einem bestimmten Punkt des gegebenen Systems.
Einflusslinien werden sowohl für Schnittgrößen und entsprechende Auflagerreaktionen als auch für Verformungen benötigt. Auch für abgeleitete Größen, wie z.B. Spannungen und Verzerrungen, sind Einflusslinien denkbar.
2.2 zweites Zitat [2]
Sind viele Lastfälle zu berücksichtigen ..., so kann das Finden... der Zustandslinien sehr aufwändig sein. Der Aufwand kann [bei Gebrauch von Einflusslinien] in Grenzen gehalten werden, wenn nicht die ... Schnittgrößen im gesamten Tragwerk gesucht sind, sondern nur an ... [bestimmten] Stellen.Anmerkung: Das Tragwerk ist i.d.R. als Ganzes optimal auszulegen, wofür die Zustandslinie/n in ganzer Länge vorliegen muss/müssen. Beispiel für eine bestimmte Stelle in obigem Sinn wäre eine Stoßverbindung innerhalb eines Tragbalkens. Eine solche ist i.d. R. geringer belastbar als die beiden verbundenen Balken und muss gesondert dimensioniert werden. Man kann die Gesamtdimensionierung mit einer Zustandslinie, die diese "Balkenschwäche" ignoriert, vornehmen und danach die "Schwachstelle" aufgrund der speziel für sie ermittelten Schnittgrößen dimensionieren (und entsprechend konstruieren).
3. Beispiele
Die gewählten Beispiele sind einfachster Art. Je drei Zustandslinien folgt eine Einflusslinie. Die Untereinanderstellung der Linien macht deren Zusammenhang deutlich und dient gleichzeitig zur Konstruktion der Einfluss- aus den Zustandslinien.
3.1 die Zustandslinie
Der erste Schritt bei Festigkeits- und Verformungsuntersuchungen in der Tragwerkstatik ist immer die Ermittlung der Beanspruchung (bzw. des Zustandes) an einer Folge von Orten am Tragwerk (Schnittstellen) infolge dessen äußerer Belastung. Bei schlanken Bauteilen (Stäbe und Balken), wie sie im Bauwesen häufig sind, ist das relativ einfach möglich und ebenfalls einfach darstellbar (Zustandslinie).
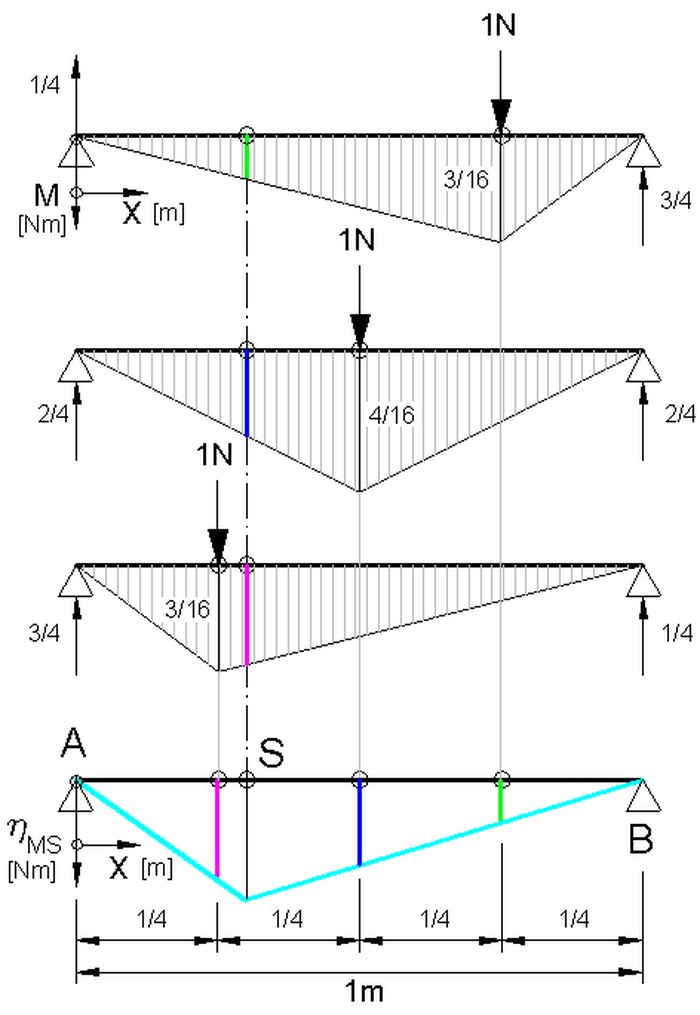Abb. 1 Balken auf 2 Stützlagern (A und B)
oben: Zustandslinien
Biegemoment M(x), verursacht
von einer einzelnen Last (1N)
unten: Einflusslinie ηMS(x), Größe des
Biegemomentes an der Stelle S in Abhängigkeit
vom Belastungsort x der Last
Konstruktion mit Hilfe der obigen Zustandslinien
Die Beanspruchungen (Längskraft, (Biege-)Moment und Querkraft) werden fortlaufend über die Länge z.B. eines Balkens in einem Zustandsdiagramm dargestellt (wobei sich die Abszisse mit dem Balken, genauer mit einer seiner Längsfasern decken kann). Der Abszissen-Nullwert ist der Balkenanfang, oder wenn es sich beispielsweise um einen horizontalen Balken auf zwei Traglagern (Brückensteg) handelt, eine der beiden Lagerstellen.
Die Zustandslinie zeigt den Zustand der Beanspruchung, der von einer oder mehreren ortsfesten Lasten (der Belastung) auf dem Balken abhängt, an jeder Stelle des Balkens an.
Aus dem über die Balkenlänge verschiedenen Beanspruchungs-Zustand kann auf die unterschiedlich notwendige Dimensionierung des Balkens geschlossen werden (unterschiedlich großer Balkenquerschnitt über die Balkenlänge).
3.2 die Einflusslinie
Während die Zustandslinien bei Festigkeits- und Verformungsuntersuchungen in der Tragwerkstatik immer gebraucht werden, arbeitet man mit Einflusslinien nur gelegentlich und dann immer nur zusätzlich.
Mit Hilfe einer Einflusslinie stellt man die Beanspruchung an einer ausgewählten Stelle (S) dar, die vom veränderlichen Angriffspunkt einer "Wanderlast" abhängt. Die Form der Einflusslinie ist nicht von der Größe der Wanderlast abhängig. Um aber die Größe der Beanspruchung aus der Einflusslinie ablesen zu können, muss die Ordinate dimensionsbehaftet skaliert sein.
a) Eine Möglichkeit ist, als Ordinate η den Quotienten aus Beanspruchung und Wanderlast F aufzutragen. Der abgelesene η-Wert ist mit F zu multiplizieren:
Beanspruchung = ηS(x) · F.
Bei Biegebeabspruchung hat η die Dimension einer Länge, bei Längs- und Querkraftbeanspruchung ist es dimensionslos.
Das Ergebnis dieser "Möglichkeit" (Bezug auf die verursachende Kraft F) ist das, was eigentlich unter dem Begriff Einflussfunktion/linie verstanden wird,
b) Ein besonderes, oft benutztes Vorgehen ist, als Wanderlast die Einheitslast 1N einzusetzen. Dann hat η bereits die zur Beanspruchungsart gehörende Dimension. Ein abgelesener "Einfluss" ist nur mit dem Quotienten aus tatsächlicher Wanderlast und Einheitslast zu multiplizieren, um den entsprechenden Zustand an der Ablesestelle zu erhalten.
In den Abb.n 1 u. 2 ist 1N als Kraft vorgegeben. Dadurch wurde auch die Konstruktion der Einflusslinien erleichtert: Übernahme entsprechender Ordinatenwerte von den Zustands-Diagrammen in die Einfluss-Diagramme in gleicher Länge, ohne dass die Ordinatenachsen der der Einfluss- anders als in den Zustandsdiagrammen zu skalieren wären.
(s. Anmerkungen).
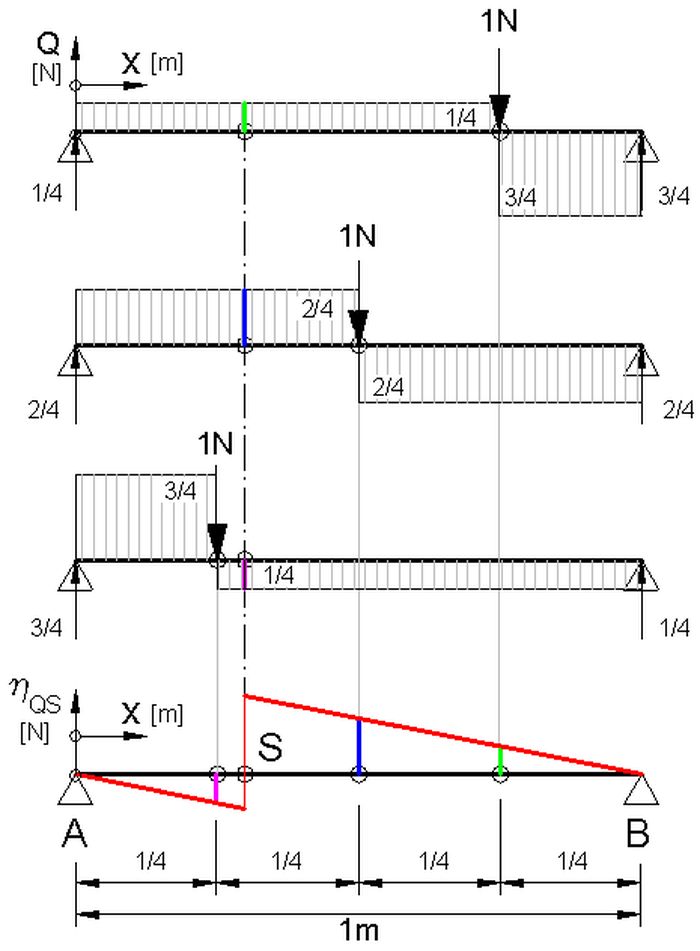Abb. 2 Balken auf 2 Stützlagern (A und B)
oben: Zustandslinien
Moment MQ(x), verursacht
von einer einzelnen Last (1N)
unten: Einflusslinie ηQS(x), Größe der
Querkraft an der Stelle S in Abhängigkeit
vom Belastungsort x der Last
Konstruktion mit Hilfe der obigen Zustandslinien
Mit Hilfe von Abb.1 und Abb.2 ist für einen Balken auf 2 Lagern der Zusammenhang zwischen Zustands- und Einflusslinie dargestellt. Für Biege- (Abb.1) und Querkraft-Beanspruchung (Abb.2) sind je 3 Zustandslinien für je 3 Orte einer einzelnen vertikalen Last gezeichnet. Die jeweiligen Beanspruchungen an einer untersuchten Stelle S des Balkens sind alle im gleichen Maßstab in das zugehörende Einflusslinien-Diagramm an der jeweiligen Stelle der Last übertragen worden. Die Verbindung dieser Werte stellt die jeweilige Einflusslinie dar.
Beide Linien bestehen aus 2 geraden Stücken. Würde der Balken nicht statisch bestimmt, sondern überbestimmt gelagert, wären die Einflusslinien gekrümmte Kurven.
Die Ausdehnung auf 3 Zustandslinien ist gleichzeitig eine Konstruktions-Methode für das Finden der Einflusslinien (Vorgehen: In Einflusslinie aus den Zustandlinien übernommene Ordinaten-Werte sind Paar-weise gleichfarbig gezeichnet). Sie ist anschaulicher als viele der in der Literatur zu findende Konstruktions-Rezepte.
Anmerkungen:
Wenn man ein Vielfaches von 1 N als Einheitslast oder eine mit einer anderen Maßeinheit versehene Einheitslast verwendet, so ist das beim erhaltenen Ergebnis selbstverständlich zu berücksichtigen.
In den beiden Abbildungen hat der Balken die Einheitslänge 1m. Die Größe der Momenten-Beanspruchung ändert sich mit der tatsächlichen Länge.
Das zweite einfache Beispiel stammt aus Quelle [2] und ist in Abb.3 gezeigt. Das Vorgehen bei der Konstruktion der Einflusslinie (Übernahme von Ordinaten-Werten aus den Zustandslinien) ist hier mit gestrichelten Linien angedeutet.
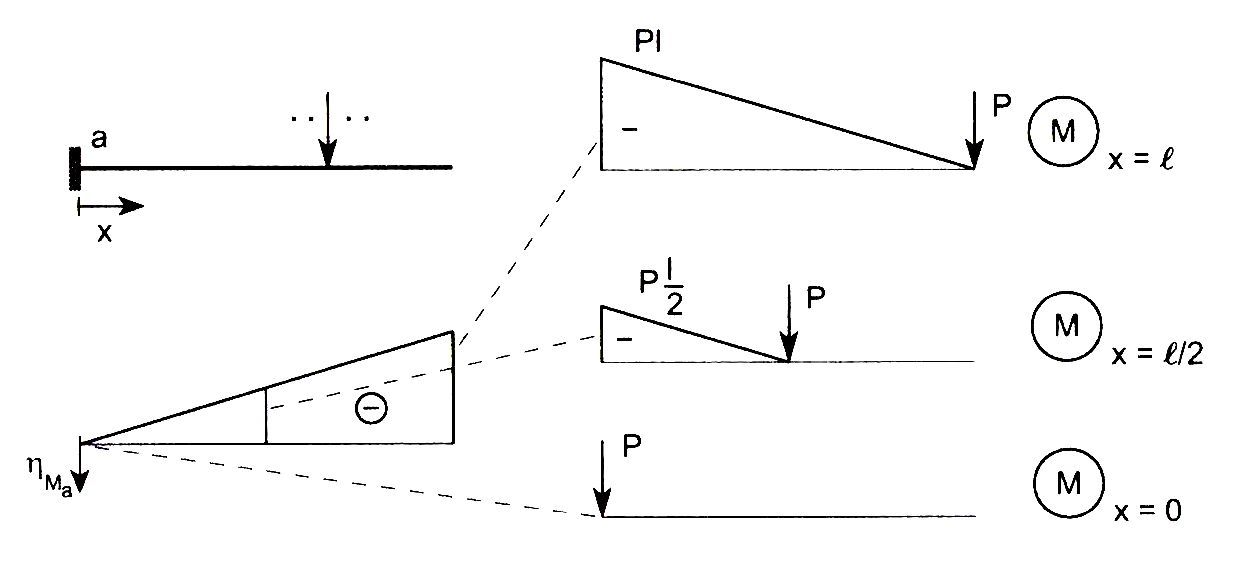Abb. 3 einseitig eingespannter Balken (Kragträger)
oben, links: bei a eigespannter Balken, schematisch
rechts: 3 Zustandslinien Moment M(x), infolge einer Einzel-Last P an 3 versch. Stellen x des Balkens
unten, links: Einflusslinie ηMa(x)
4. Schlussbemerkungen
In Abb.1 ist die Einflusslinie den Zustandslinien zum Verwechseln ähnlich.
In Abb.3 sind die Linien zueinander wenigstens nur spiegelgleich.
Einen unmittelbaren Gewinn an Information liefern beide Beispiele nicht.
Auch ohne Kenntnis der Existenz einer Einflusslinie ist allgemein bekannt,
* dass beim Balken auf zwei Lagern die Biegebeanspruchung bei mittiger Last und in der Mitte maximal ist und
* dass beim Kragträger die Biegespannung bei Last am freien Ende an der Einspannstelle maximal
und bei Last an der Einspannstelle selbstverständlich überall Null ist.
Etwas ist mir nach einer gewissen Angewöhnungs-Zeit noch geblieben: Mit der Einflusslinie gewinnt man einen "Hingucker". Sie zeigt nämlich sehr anschaulich, wie sich die Beanspruchung an einer beliebigen Balkenstelle bei einer auf dem Balken "wandernder" Last ändert. Der Hingucker kann besonders schön in einer Animation sein, worin die Änderung der Einflußlinie fortlaufend mit der Lastwanderung dargestellt ist.
5. Quellen
[1] ETH, Zürich, Einflusslinien für statisch unbestimmte Systeme, S.3[2] Dieter Dinkler: Grundlagen der Baustatik, Springer/Vieweg, 4.Aufl., S.134/35
Siegfried Wetzel, CH 3400 Burgdorf, May 2017 (Jan.20, Febr.23)
↑↑ Anfang
<< andere Mechanik-Beiträge
<< Home