<< Home
<< anderes Geometrisches
↓↓ Ende
Die Platonischen Körper - eine Annäherung
Inhalt
1. Einleitung
2. Die fünf möglichen Körperecken
3. Schrittweise Ergänzung zur Oberfläche eines Polyeders
3.1 Tetraeder
3.2 Oktaeder
3.3 Ikosaeder
3.4 Hexaeder
3.5 Dodekaeder
4. Anhang
4.1 Oktaeder und Hexaeder
4.2 Ikosaeder und Dodekaeder
4.3 Ebene Schnitte durch Platonische Körper entlang von Kanten
4.4 Ebene Schnitte durch Platonische Körper, nicht entlang von Kanten
4.4.1 Tetraeder
4.4.2 Oktaeder
4.4.3 Ikosaeder
4.4.4 Hexaeder
4.4.5 Dodekaeder
4.5 Antiprismen
5. Literatur
1. Einleitung ↑ Anfang
Die Platonischen Körper sind den meisten Menschen bekannt als diejenigen fünf Körper, deren Oberfläche ausschließlich aus einer bestimmten Anzahl bestimmter gleichmässiger Vielecke (Polygone) besteht. Die aus den Kanten der Polygone gebildeten Ecken eines Platonischen Körpers haben alle die gleiche Form.
Diese Körper waren schon früh in der Antike bekannt, wurden aber erst vom griechischen Philosoph Platon im 4. Jahrhundert v. Chr. ausführlich besprochen [1] und von ihm ihren Namen bekamen. Einen ersten die Platonischen Körper betreffenden Beweis, nämlich den dafür, dass es nur fünf Möglichkleiten für aus Kanten gebildete Körper-Ecken gibt, erbrachte ein Schüler Platon's, der Mathematiker Theaitetos. Euklid nahm die Platonischen Körper inkl. dieses Beweises in sein Werk Elemente auf [2]. Ich werde diesen Beweis über die auf fünf beschränkte Zahl von Körper-Ecken ansprechen.
Dass die jeweils mit ausschließlich einer dieser Ecken-Form gebildeten Körper tatsächlich die fünf Platonischen Körper sind, zeige ich dadurch, dass man zu ihnen kommt, wenn man beginnend mit einer ersten Ecke fortlaufend weitere gleiche Polygone zufügt. Je nach Platonischem Körper besteht die erste Ecke - wie alle Ecken - des Körpers aus drei vier oder fünf entsprechenden Polygonen. Beim Zufügen vergrößert sich die Ecken-Zahl. In allen fünf Fällen entsteht schließlich eine geschlossene Hülle bzw. die geschlossene Oberfläche des betreffenden Platonischen Körpers. Dabei wurden jeweils genau so viele Poplygone zusammen gebaut, wie für den jeweiligen Platonischen Körper kennzeichnend sind. Es entstand auch die jeweils kennzeichnende Zahl räumlicher Ecken und Körperkanten.
In einem Anhang weise ich auf einige interessante Einzelheiten hin, die mir während meiner geometrischen Annäherung an die Platonischen Körper sonst noch und eher zufällig (keine systematischen Betrachtungen, deshalb die unverbindliche Überschrift "Anhang)" auffielen.
2. Die fünf möglichen Körperecken ↑ Anfang
Damit eine Körperecke entsteht, müssen mindestens drei Kanten von ihr ausgehen. An diesen stoßen je zwei Polygone zusammen, von denen je eine Seite die gemeinsame Kante bilden. Je eine Ecke der mindestens drei Polygone treffen sich in der Körperecke.
Eine Körperecke entsteht nur, wenn die Summe der Innenwinkel der Polygone kleiner als 360° ist. Wäre sie gleich 360°, würden die Flächen in einer Ebene liegen (bei mehr als 360° würden sie sich teilweise überlappen, eine Körperecke wäre prinzipiell nicht möglich).
Diese beiden Bedingungen werden nur von fünf Körpern - den Platonischen Körpern - erfüllt. Als gleichseitige Flächen (Polygone) kommen nur Dreieck, Quadrat und Fünfeck in Frage. Beim gleichseitigen Sechseck ist bereits die Summe aus drei Innenwinkeln gleich 360°. Platonische Körper mit gleichseitigen Dreiecken haben bis zu fünf an einer Körperecke zusammenstoßende Flächen, weil der Innenwinkel eines Dreiecks nur 60° beträgt (Abb.1; die Situation bei Verwendung der anderen Polygone ist auch in dieser Tabelle zusammenfassend geschildert).

Abb.1 fünf mögliche Körperecken aus drei oder mehr Polygonen unter Bedingung: Ecksummenwinkel kleiner als 360°
Tabelle: Wikipedia
3. Schrittweise Ergänzung zur Oberfläche eines Polyeders ↑ Anfang
Für jeden der Platonischen Körper mit der in Abb.1 eingetragenen, ihn kennzeichnenden Körperecke wird gezeigt, dass durch Zufügen gleicher Polygone - beginnend an einer ersten Ecke bzw. Flächengruppe (Flächen-Tupel) - immer weitere gleiche Körperecken entstehen, und dass nicht eine beliebige und nicht eine beliebig große Flächengruppe, sondern schlussendlich die geschlossene Oberfläche des Platonischen Körpers entsteht.
3.1 Tetraeder ↑ Anfang
4 Flächen (Dreiecke), 4 Ecken, 6 Kanten
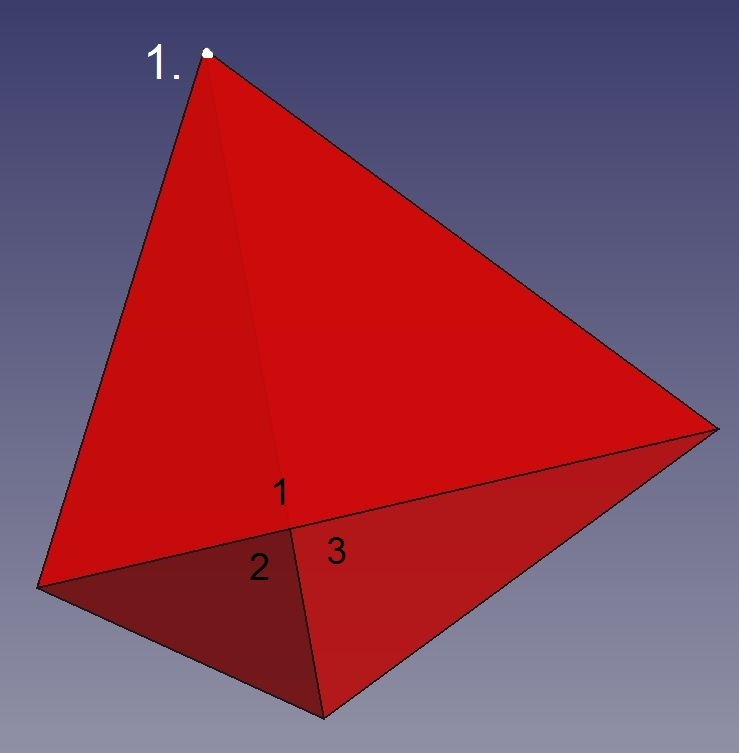
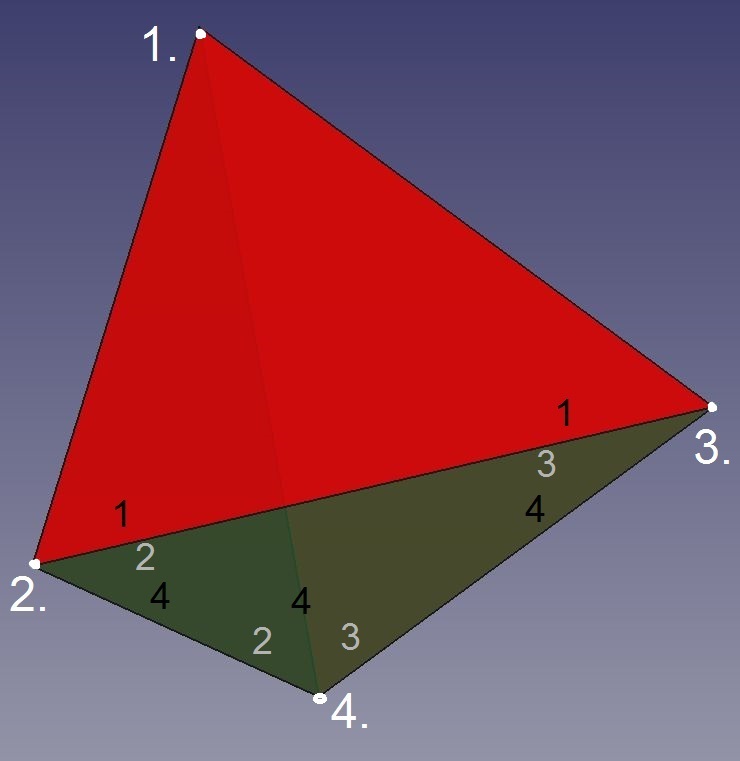
Abb.2 Tetraeder
Die erste Ecke (1.) wird von den drei Dreiecken 1 bis 3 gebildet.
Diese "Tüte" wird bereits durch Zufügen nur eines Dreiecks (4) zur Oberfläche des Tetraeders geschlossen. Dabei entstehen die wie 1. gleichartigen Körperecken 2. bis 4.
3.2 Oktaeder ↑ Anfang
8 Flächen (Dreiecke), 6 Ecken, 12 Kanten
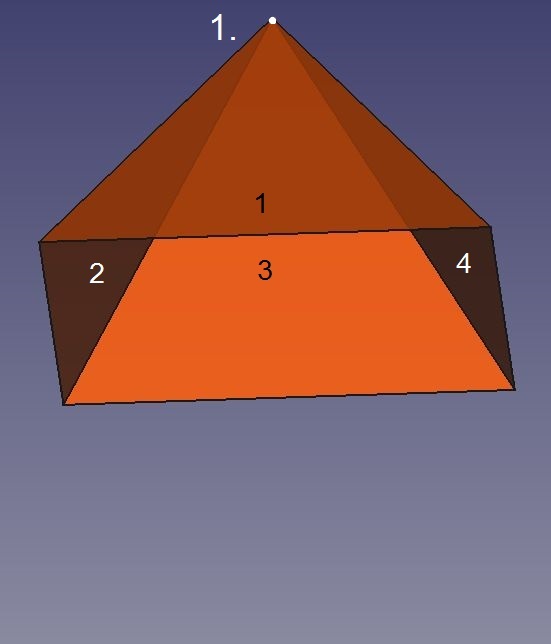
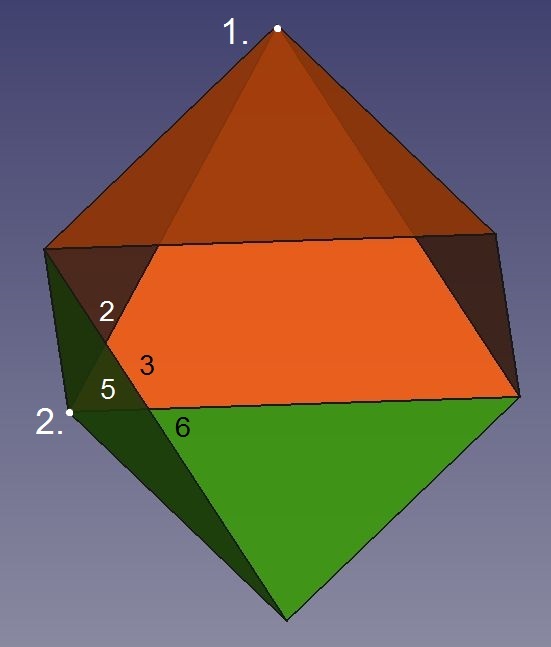 Abb.3a Oktaeder
Abb.3a Oktaeder
Die erste Ecke (1.) wird von den vier Dreiecken 1 bis 4 gebildet.
Damit die zweite Ecke (2.) entsteht, müssen zwei weitere Dreiecke (5 und 6) an diese "Tüte" angeschlossen werden. Nur ein Dreieck genügt nicht, da eine Oktaeder-Ecke von vier Dreiecken gebildet wird. Dort, wo eine zweite Ecke zu bilden ist, nämlich am "freien" Ende einer von der ersten Körperecke weglaufenden Kante, stoßen bisher aber nur zwei Dreiecke zusammen.
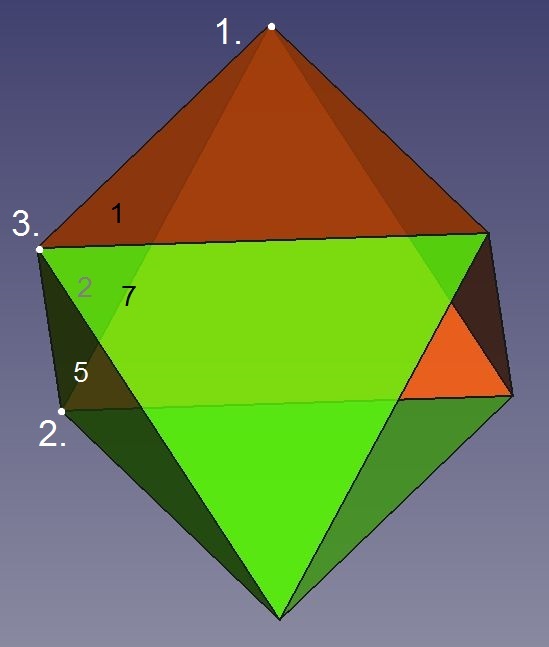
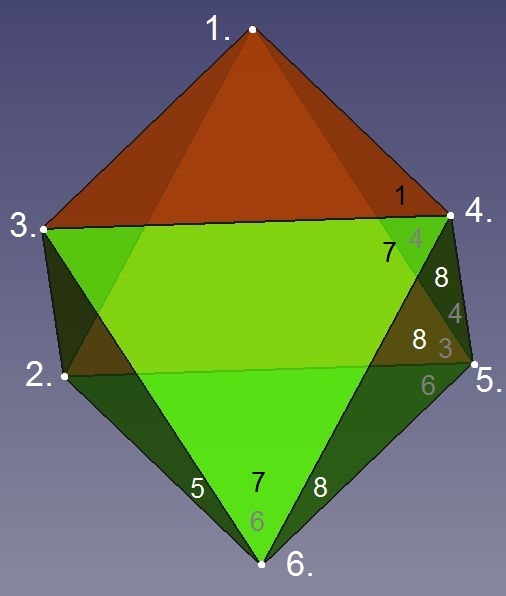 Abb.3b Oktaeder
Abb.3b Oktaeder
Zur Bildung einer weiteren vier-flächigen Körperecke (3.) genügt der Anschluss nur eines weiteren Dreiecks (7), denn das schon vorhandene Dreieck (6) ist an ihr beteiligt.
Durch Anschluss des letzten Dreiecks (8) wird die Oberfläche des Oktaeders komplettiert. Dabei entstehen auf einmal die drei Körperecken (4., 5. und 6.).
3.3 Ikosaeder ↑ Anfang
20 Flächen (Dreiecke), 12 Ecken, 30 Kanten
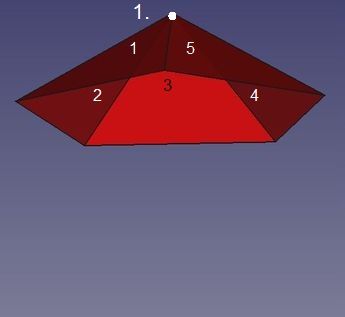
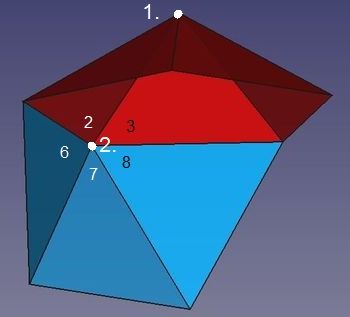 Abb.4a Ikosaeder
Abb.4a Ikosaeder
Die erste Ecke (1.) wird von den fünf Dreiecken 1 bis 5 gebildet.
Damit eine zweite Ecke (2.) entsteht, müssen drei weitere Dreiecke (6 bis 8) an diesen "Regenschirm" angeschlossen werden. Nur ein Dreieck genügt nicht, da eine Ikosaeder-Ecke von vier Dreiecken gebildet wird. Dort, wo eine zweite Ecke zu bilden ist, nämlich am "freien" Ende einer von der ersten Körperecke weglaufenden Kante, stoßen bisher aber nur zwei Dreiecke zusammen.
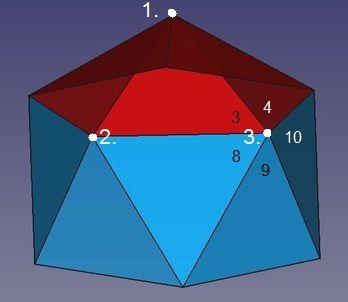
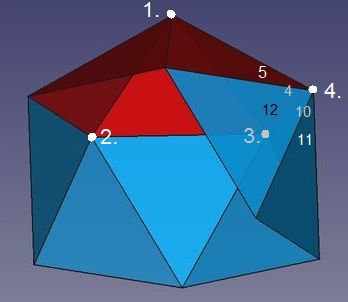 Abb.4b Ikosaeder
Abb.4b Ikosaeder
Damit eine dritte Ecke (3.) entsteht, müssen nur zwei weitere Dreiecke (9 und 10) an diesen "Regenschirm" angeschlossen werden, denn als fünftes Dreieck fungiert das im Schritt vorher angeschlossees Dreieck 8.
Eine nächste Ecke (4.) lässt sich analog wie die vorherige (3.) bilden. Neue Dreiecke sind 11 und 12.
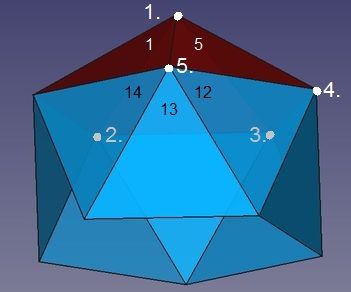
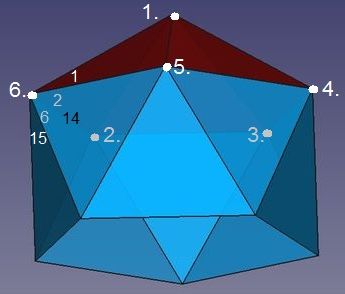 Abb.4c Ikosaeder
Abb.4c Ikosaeder
Analog wie die Ecken 3. und 4. lässt sich auch die Ecke 5. bilden. Neue Dreiecke sind 13 und 14.
Das um den Rand des ersten Flächen-Quintupels (Ecke 1., Dreiecke 1 bis 5) laufende Band benötigt für seinen Zusammenschluss nur noch ein Dreieck. Es wird mit Dreieck 15 geschlossen, wobei die Körperecke 6. entsteht.
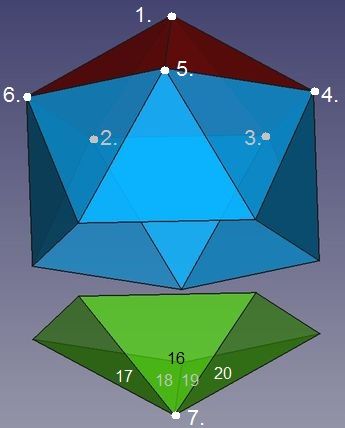
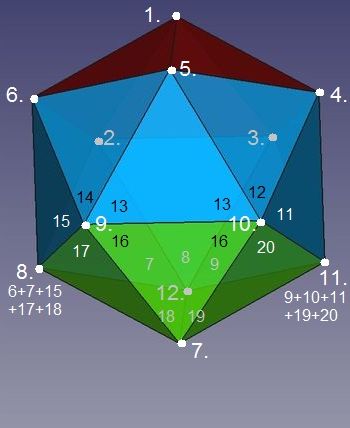 Abb.4d Ikosaeder
Abb.4d Ikosaeder
Der sich in einer Ebene befindende geknickte untere Rand des bisher 15-Flächners ist die Gegenkontur zum Rand eines mit dem Flächen-Quintupel 1 bis 5 identischen Fünflächners. Links unten wird dieser den Ikosaeder vervollstädigende "Boden" aus den Dreiecken 16 bis 20 gezeigt. Er ist in seiner rotatorischen Symmetrieachse um 36° gegenüber dem oben befindlichen "Deckel" verdreht.
Das rechte Bild zeigt den mit dem 15-Flächner vereinigten "Boden". An allen fünf Knickstellen im Rand ist je eine Körperecke entstanden (8. bis 12.). Die "Boden"-Spitze ist die Körperecke 7. .
Je zwei Ecken auf dem Ikosaeder liegen sich diagonal gegenüber (1. und 7., 6. und 11., usw.). Die aus den sich in ihnen treffenden Kanten gebildeten Strahlen-Sterne sind gegeneinander um 36° verdreht
3.4 Hexsaeder ↑ Anfang
6 Flächen (Quadrate), 8 Ecken,12 Kanten
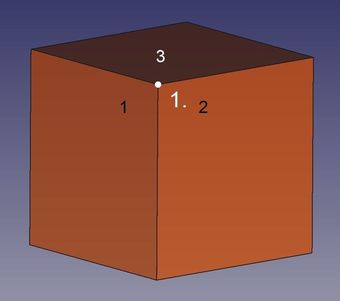
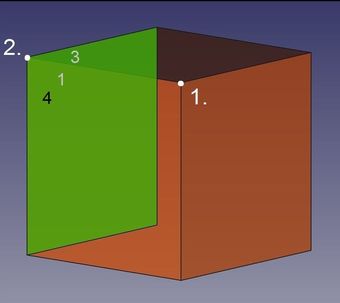 Abb.5a Hexaeder
Abb.5a Hexaeder
Die erste Ecke (1., im Bild von innen gesehen !) wird von den drei Quadraten 1 bis 3 gebildet.
Damit die zweite Ecke (2.) entsteht, genügt der Anschluss nur eines weiteren Quadrats (4) an diesen "Dreispitz", denn die Körperecke des Hexaeders wird von nur drei Teilflächen (Quadraten) gebildet. Und dort, wo eine zweite Ecke zu bilden ist, nämlich am "freien" Ende einer von der ersten Körperecke weglaufenden Kante, stoßen bisher bereits zwei Quadrate zusammen.
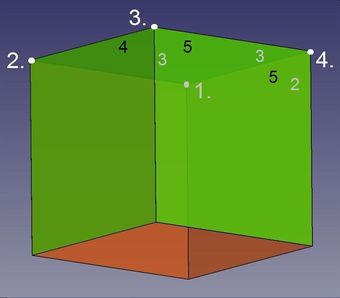
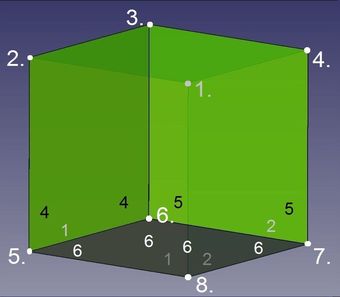 Abb.5b Hexaeder
Abb.5b Hexaeder
Durch Zufügen nur eines Quadrats (5) entstehen gleich zwei weitere Körperecken (3. und 4.). Die Bildung der Ecke 4. ist gleich erklärbar wie die der Ecke 2., während Quadrat 5 zusammen mit Quadrat 3 und dem vorher zugefügten Quadrat 4 die Ecke 3. bilden.
Der inzwischen entstandene kopfstehende "Kasten" wird durch Zufügen des Quadrats (6) zur Oberfläche des Hexaeders geschlossen. Dabei entstehen auf einem Schlag die Körperecken 5. bis 8., die je mit je zwei zusammen stoßenden Quadraten vorbereitet waren.
3.5 Dodekaeder ↑ Anfang
12 Flächen (Fünfecke), 20 Ecken, 30 Kanten
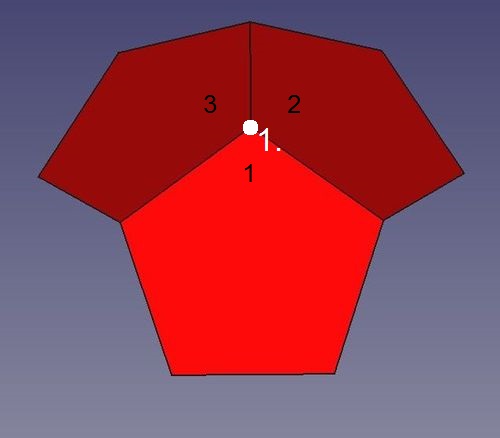
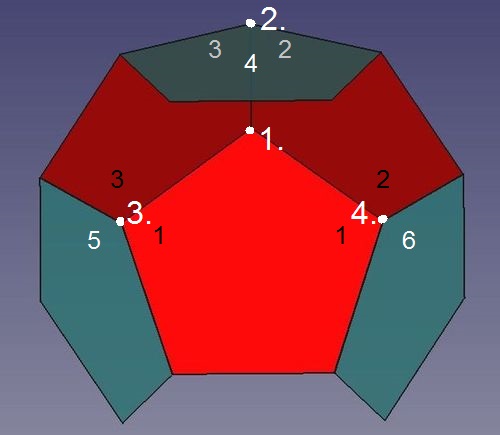 Abb.6a Dodekaeder
Abb.6a Dodekaeder
Die erste Ecke (1., im Bild, von innen gesehen !) wird von den drei Fünfecken 1 bis 3 gebildet.
Damit die zweite Ecke (2.) entsteht, genügt der Anschluss nur eines Fünfecks (4) an diese "Kappe", denn die Körperecke des Dodekaeders wird von nur drei Teilflächen (Fünfecken) gebildet. Und dort, wo eine zweite Ecke zu bilden ist, nämlich am "freien" Ende einer von der ersten Körperecke weglaufenden Kante, stoßen bisher bereits zwei Fünfecke zusammen.
Die Ecken 3. und 4. werden analog wie Ecke 2. gebildet. Zwischen den Fünfecken 4 bis 6 bleiben vorerst drei Lücken bestehen.
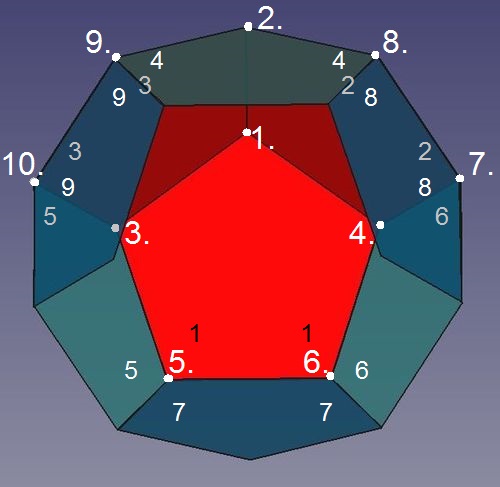
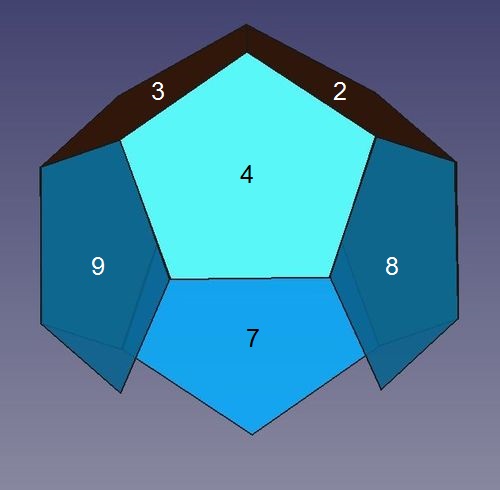 Abb.6b Dodekaeder
Abb.6b DodekaederIn die Lücken zwischen den Fünfecken 4 bis 6 werden die Fünfecke 7 bis 9 eingefügt, die mit den vorhandene Fünfecken je zwei weitere Körperecken bilden: 5. bis 10. .
Zur Vorbereitung der nächsten Schritte ist der bisher entstandene Neunflächner nach vorn gekippt gezeigt: auf Kopf stehender "Behälter", rechts im Bild.
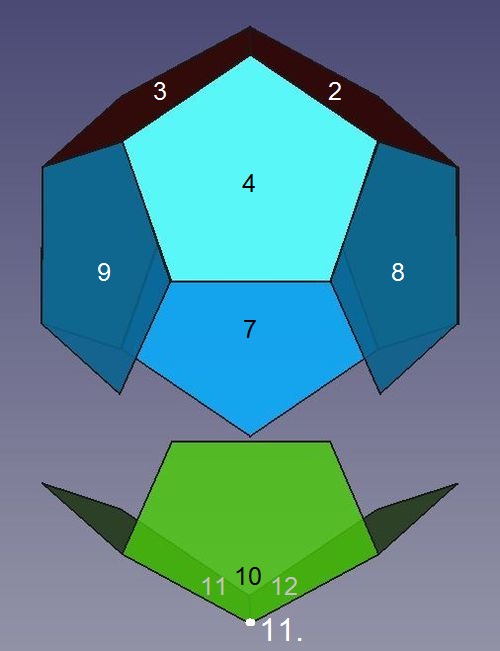
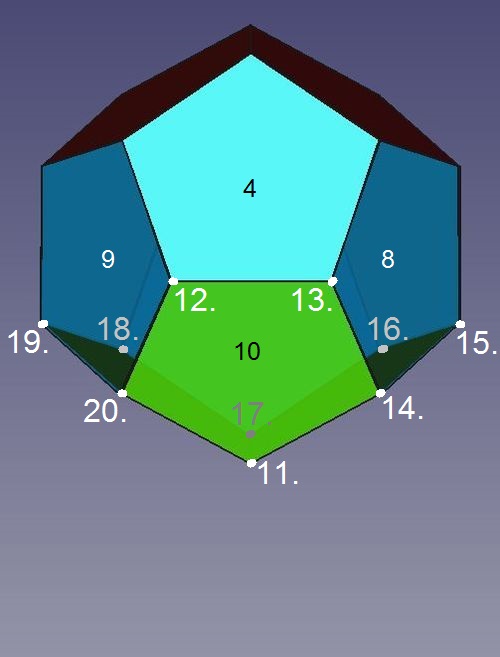 Abb.6c Dodekaeder
Abb.6c DodekaederDer gezackte Rand des "Behälters" ist die Gegenkontur zum Rand eines mit der "Kappe" identischen Dreiflächners. Links unten wird dieser den Dodekaeder vervollstädigende "Boden" aus den Fünfecken 10 bis 12 gezeigt.
Das rechte Bild zeigt den mit diesem "Boden" ergänzten "Behälter". An allen neun Knickstellen im Rand ist je eine Körperecke entstanden (11. bis 19.). Die "Boden"-Spitze ist die Körperecke 20. .
Je zwei Ecken auf dem Dodekaeder liegen sich diagonal gegenüber (z.B. 1. und 20., Nummerierung nur für vorliegende Herleitung relevant). Die aus den sich in ihnen treffenden Kanten gebildeten Strahlen-Sterne sind gegeneinander um 60° verdreht.
4. Anhang ↑ Anfang
4.1 Oktaeder und Hexaeder ↑ Anfang
Beim Oktaeder und beim Hexaeder habe ich - ausgehend von der Zahl der Teilflächen, die für die erste Körperecke nötig sind - durchgehend immer nur eine Teilfläche zugefügt.
Beim Ikosaeder und beim Dodekaeder habe ich jeweils am Schluss eine Abkürzung vorgenommen, indem ich eine der anfänglichen Gruppe gleiche teilflächen-Kombination als schließenden "Boden" anfügte.
Im folgenden wende ich dieses Vorgehen auch beim Oktaeder und beim Hexaeder an. Das führt zu einem sehr kurzen Vorgehen, denn zusammenzufügen sind lediglich die anfängliche "Tüte" bzw. der anfängliche "Dreispitz" und der schließende "Boden".
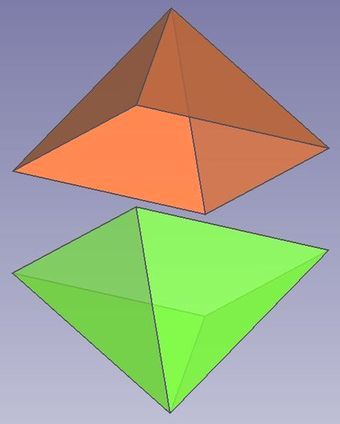
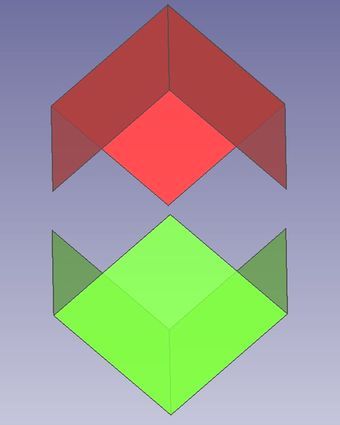 Abb.7 Oktaaeder und Hexaeder:
Abb.7 Oktaaeder und Hexaeder:
Aufteilung der Oberflächen in je zwei zusammenpassende, aus wenigen Polynomen bestehende Eckteile.
4.2 Ikosaeder und Dodekaeder ↑ Anfang
Ikosaeder und Dodekaeder sind die komplexesten Gebilde der fünf Polyeder. Bei meinen Versuchen, mit ihnen näher vertraut zu werden, habe ich ihre Oberflächen unterschiedlich in größere Teile zerlegt.
Bei ihrem schrittweisen Zusammenbau (Abschnitt 3.) fiel mir ihre Unterteilung in je drei Bereiche auf. Zwischen "Regenschirm" bzw. "Kappe" am Anfang und "Boden" am Schluss befindet sich ein aus den jeweiligen Polynomen bestehender "Gürtel". Sein Herausstellen trägt zur Anschaulichkeit im Umgang mit diesen beiden Platonischen Körpern bei.
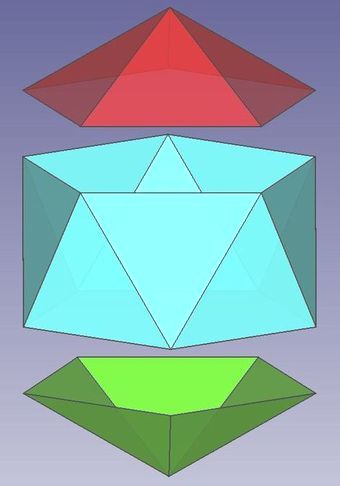
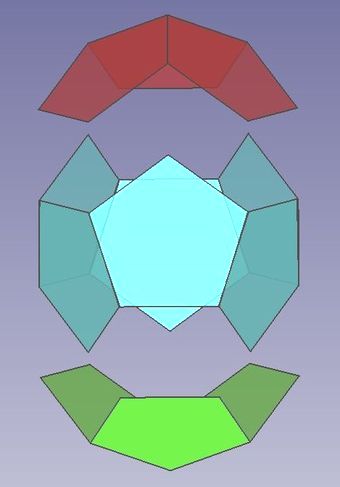 Abb.8 Ikosaeder und Dodekaeder: Aufteilung der Oberflächen in je drei Bereiche
Abb.8 Ikosaeder und Dodekaeder: Aufteilung der Oberflächen in je drei Bereiche
Der "Gürtel" beim Ikosaeder in der Mitte (10 Dreiecke) ist Oberflächenteil eines sogenannten
uniformen Antiprismas (fünfeckiges Antiprisma: Deck- und Grundfläche sind gleichseitige Fünfecke).
Die Oberflächen von Ikosaeder und Dodekaeder lassen sich auch in zwei gleiche Bereiche aufteilen. Diese "Schalen" stehen aber nicht je auf einer Polyeder-Spitze sondern je auf einer Polyeder-Teilfläche (Polygon).
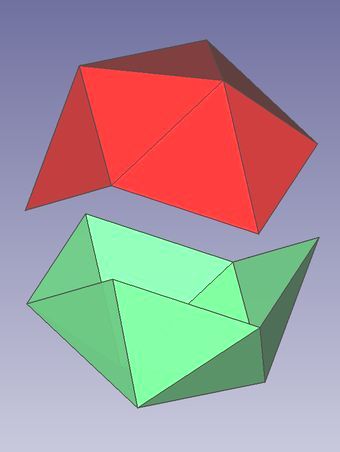
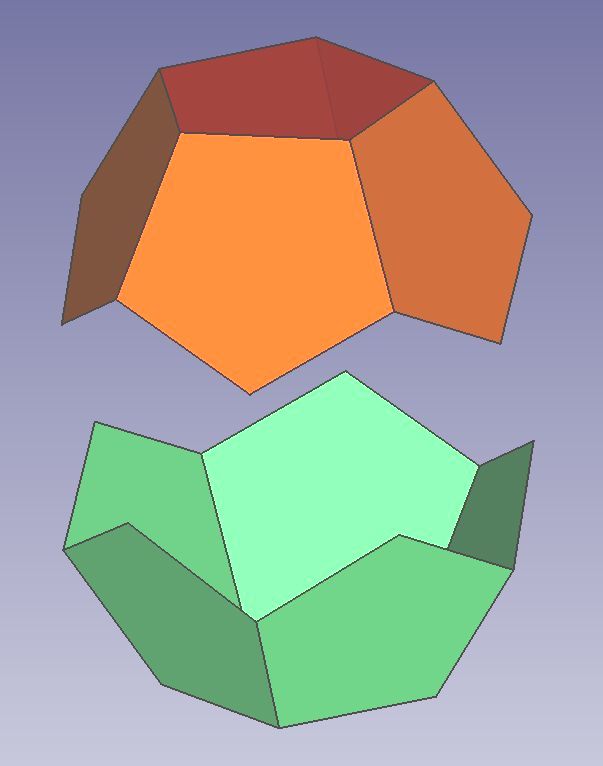 Abb.9 Ikosaeder und Dodekaeder: Aufteilung der Oberflächen in je zwei zusammenpassende Teile.
Abb.9 Ikosaeder und Dodekaeder: Aufteilung der Oberflächen in je zwei zusammenpassende Teile.
4.3 Ebene Schnitte durch Platonische Körper entlang von Kanten ↑ Anfang
Die oben (4.1 und 4.2) besprochenen Teilungen der Oberflächen der Platonischen Körper in zwei bzw. drei Bereiche führten zur Frage, ob man einen kompletten, voluminösen Platonischen Körper mit einem ebenen Schnitt, der an der Oberfläche ausschließlich durch Kanten führt, teilen kann. Ich fand eine solche Möglichkeit nur für das Oktaeder und für das Ikosaeder. Nur bei diesen beiden Körpern gibt es je einen von in einer Ebene liegenden Kanten gebildeten Linienkranz.
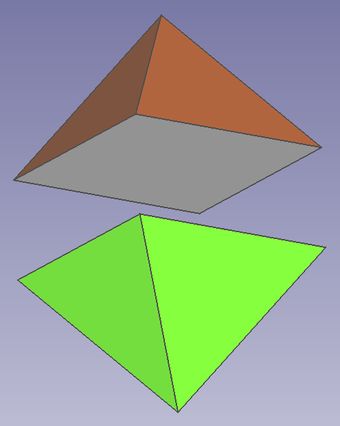
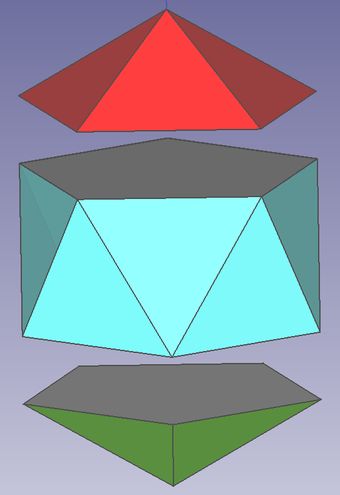 Abb.10 ebene Körper-Schnitte entlang von Kanten
Abb.10 ebene Körper-Schnitte entlang von Kanten
links: Oktaeder (s.a. Abb.6, links), mittiger Schnitt in zwei gleicheTeile
rechts: Ikosaeder (s.a. Abb.7, links), außermittige Schnitte in drei Teile
4.4 Ebene Schnitte durch Platonische Körper, nicht entlang von Kanten ↑ Anfang
Noch nicht genug der Teilungen von Platonischen Körpern. Im Deckblatt meiner Artikel-Gruppe Geometrisches befindet sich als "Aufhänger" das Bild einer Plastik von Max Bill (s.a. Abb.13b). Welchen Platz nimmt das dort gezeigte, durch Halbieren eines Hexaeders (Würfels) entstandene sechseckige Schnittbild in der wahrscheinlich riesigen Zahl von Schnittbildern ein, die bei (ebenem) Durchschneiden Platonischer Körper entstehen können?
Die bei beliebig geführten Schnitten durch die Platonischen Körper entstehenden Schnittfiguren sind vielfältig, aber nicht beliebig manigfaltig.
Es ist nur eine beschränkte Anzahl von im Allgemeinen unregelmäßigen Polygon-Typen (..-Eck) möglich. Die folgende Aufstellung betrifft nur Schnitte, die ausschließlich durch Körperkanten führen (durch eine oder mehrere Ecken führende sind nicht beachtet):
Plat.Körper mögliche Polygone (Körperecken-Zahl im Abschnitt)
---------------------------------------------------------------------
Tetraeder 3- (1) oder 4-Eck (2)
Oktaeder 4- (1) oder 6-Eck (2 o. 3)
Ikosaeder 5- (1), 8- (2), 9- (3), 10- (4 o. 6) oder 11-Eck (5)
Hexaeder 3- (1), 4- (2 o. 4), 5- (3) oder 6-Eck (4)
Dodekaeder 3- (1), 4- (2), 5- (3), 6- (4, 6 o. 10) o. 8-Eck (6 o. 8)
Man findet diese Möglichkeiten systematisch z.B. durch mit einem gemeinsamen Schnitt erfolgtes Abschneiden von Körperteilen mit immer mehr darin enthaltenen Körperecken.
In meinen Beispielen sind die Schnittflächen teilweise regelmäíg, wenigstens aber um eine (in den Abbildungen) horizontale Linie symmetrisch. Bei allgemeinen, auch räumlich schiefen Schnitten fehlt jegliche Regelmäßigkeit.
4.4.1 Tedraeder ↑ Anfang
Das 3-Eck ist naheliegend: Abschneiden einer Körperecke (eines Flächen-Tripels).
Ein 4-Eck entsteht, wenn unter einer der Kanten geschnitten wird (gemeinsames Abschneiden von zwei Körperecken).
Mehr ist nicht relevant, denn Abschneiden von 3 Körperecken ist wie Abschneiden einer (1) Ecke, nur von der gegenüberliegenden Körperseite aus begonnen.
4.4.2 Oktaeder ↑ Anfang
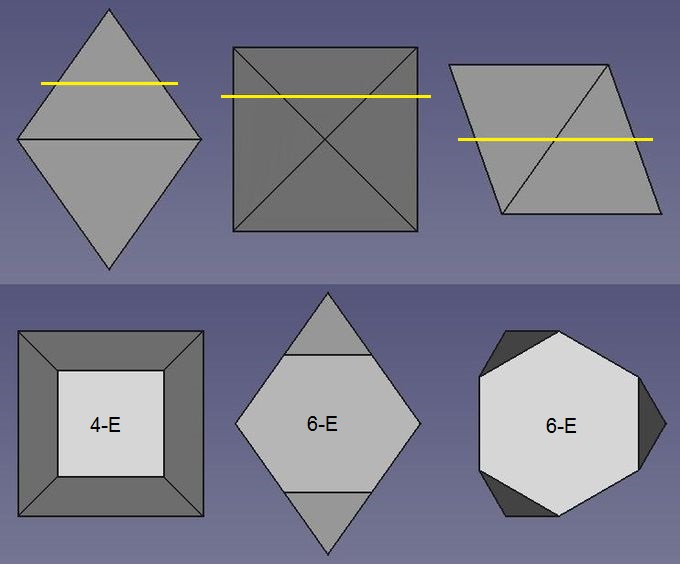 Abb.11 Schnitte durch ein Oktaeder
Abb.11 Schnitte durch ein Oktaeder
Ein 6-Eck entsteht, wenn unter einer der Kanten geschnitten wird (gemeinsames Abschneiden von 2 Körperecken, 2.Teilbild).
Weil ein Oktaeder 6 Körperecken hat, ist auch gemeinsames Abschneiden derer 3 relevant. Dabei entsteht ebenfalls ein 6-Eck (3.Teilbild).
Anmerkungen: Die Schnitte sind so gelegt, dass regelmäßige Polygone entstehen, um einen Bezug zu Abschnitt 4.4.4 (Hexaeder) herzustellen. Insbesondere geht es dabei um das regelmäßige 6-Eck in Körpermitte (3. Teilbild; das 6-Eck im 2.Teilbild ist nur in genau der vorgenommenen Schnitthöhe regelmäßig).
4.4.3 Ikosaeder ↑ Anfang
Das Fünfeck ist naheliegend, denn von einer Ecke gehen fünf Kanten aus, so dass ein solches beim Abschneiden einer Ecke entsteht (Abb.12, 1. Teilbild).
Ebenso leicht vorhersagbar ist, dass ein 10-Eck entsteht, nämlich beim Schneiden durch den Mittelteil des Körpers (4. Teilbild). Dieser ist von 10 der insgesamt 30 Kanten umgeben. An der Stelle jeder Kante hat die Schnittfigur eine (1) Ecke. Durch einzelnes Abschneiden aller Ecken ensteht der früher gebräuchliche Fußball mit 12 (regelmäßigen) 5-Ecken und 20 aus den Körperflächen-3-Ecken hervorgegangenen (regelmäßigen) 6-Ecken (abgestumpftes Ikosaeder).
Ein 10-Eck entsteht auch beim gemeinsamen Abschneiden von 4 Ecken (3. Teilbild).
Ein 8-Eck entsteht, wenn unter einer (1) der Kanten geschnitten wird (gemeinsames Abschneiden von 2 Körperecken, 2. Teilbild). 2 der von den beiden Körperecken ausgehenden insgesamt 10 Kanten sind die gemeinsame Kante, um die herum geschnitten wird.
Dass ein 9-Eck entstehen kann, mag überraschen: nach dem gemeinsamen Abschneiden von 3 Körperecken (5. Teilbild).
Dass auch eine Schnittfläche mit 11 Ecken möglich ist, mag nochmals überraschen: nach dem gemeinsamen Abschneiden von 5 Körperecken (6. Teilbild).
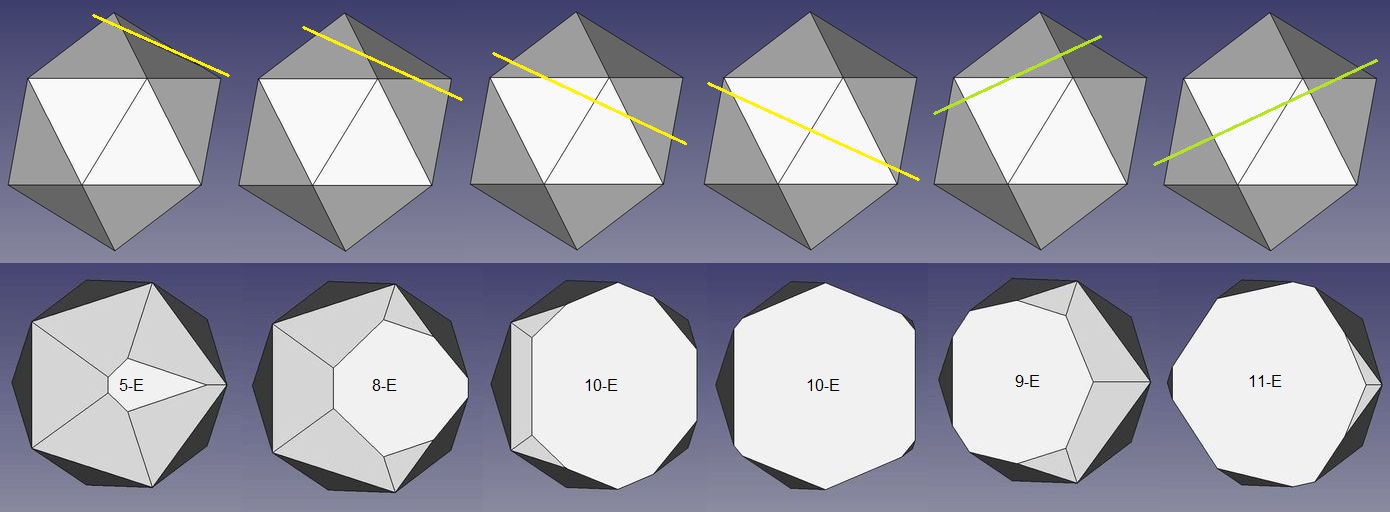 Abb.12 Schnitte durch ein Ikosaeder (Schnittebenen im 5. u. 6. Teilbild 180° um die vertkale Achse verdreht)
Abb.12 Schnitte durch ein Ikosaeder (Schnittebenen im 5. u. 6. Teilbild 180° um die vertkale Achse verdreht)
4.4.4 Hexaeder ↑ Anfang

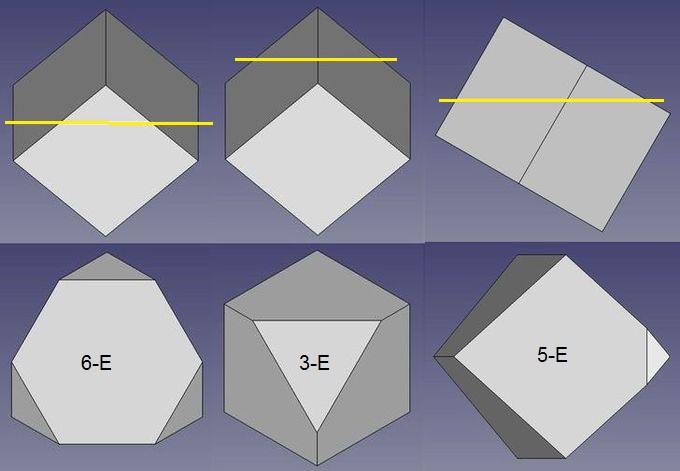 Abb.13b Schnitte durch ein Hexaeder
Abb.13b Schnitte durch ein Hexaeder
(drei von vier Möglichkeiten)
Abb.13a Schnitte durch ein Hexaeder (halbierter Würfel)
regelmäßiges Sechseck in der Kunst als Schnitt senkrecht zur und in der Mitte einer Raumdigonalen [3]
Dass unvermutete Entstehen anderer als vierseitiger Polynome beim Schneiden des äußerlich nur mit rechten Winkeln behafteten Hexaeders (Würfels) hat den Künstler Max Bill fasziniert und ihn zu entsprechenden Plastiken angeregt. Abb.13a zeigt die bekannteste davon, nämlich zwei Würfelhälften mit (regelmäßigem) 6-Eck als Schnittfigur.
Ihm ging es offenbar um Schnitte in zwei gleiche Würfelhälften. Schnitte in zwei gleiche Hälften heißt bei allen Platonischen Körpern, dass jede Hälfte gleich viele Körperecken hat. Der Würfel kann auch so in zwei gleiche Hälften zerschnitten werden, dass ein 4-Eck ensteht, was aber Bill vermutlich für zu wenig "spektakular", weil für zu wenig überraschend, hielt (auch von mir nicht in Abb.13b aufgenommen).
Das nahe liegende 3-Eck (Abb.13b, 2.Teilbild) schied aus, weil dafür nur eine (1) Körperecke abgeschnitten werden muss und keine Körperhalbierung erfolgt.
Für mich war überraschend, dass man am Würfel auch eine 5-eckige Schnittfigur erzeugen kann (gemeinsames Abschneiden von 3 Körperecken, 3. Teilbild). Für Bill schied sie - abgesehen von nicht möglicher Würfel-Halbierung - wohl schon deshalb aus, weil kein regelmäßiges 5-Eck möglich ist. Sein 6-Eck ist ein gleichmäßiges Polygon, was ästhetisch höher als ein ungleichmäßiges bewertet wird.
4.4.5 Dodekaeder ↑ Anfang
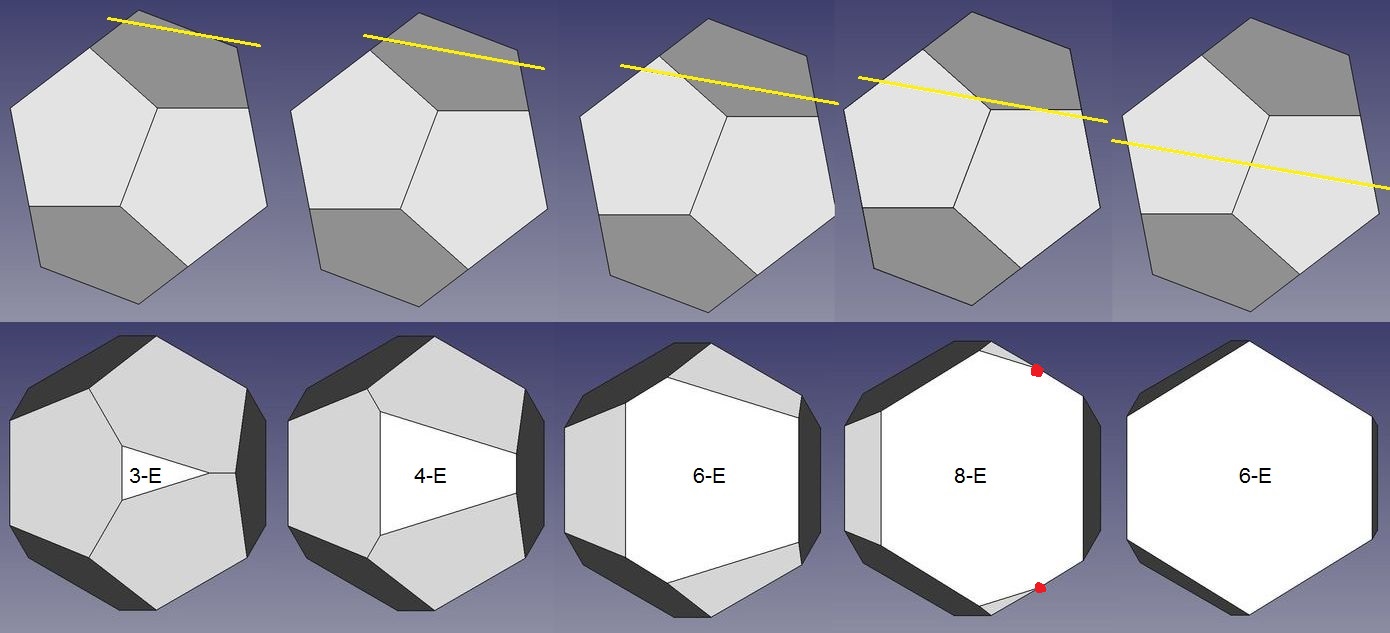
Abb.14a Schnitte durch ein Dodekaeder (Schnittebenen schräg nach rechts unten)
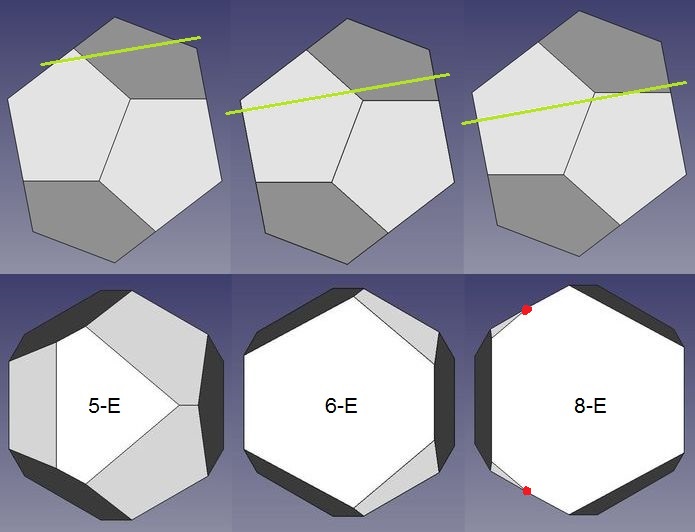 Abb.14b Schnitte durch ein Dodekaeder
Abb.14b Schnitte durch ein Dodekaeder
(Schnittebenen schräg nach links unten)
Das Dodekaeder ist das am wenigsten überschaubare der Platonischen Körper, obwohl es weniger Teiloberflächen als das Ikosaeder hat (nur 12 gegenüber 20). Folglich ist die Zahl der prinzipiell möglichen Körperschnitte größer als beim Ikosaeder (8 gegenüber 6).
Das 3-Eck ist naheliegend, denn von einer (1) Körperecke gehen 3 Kanten aus, so dass ein solches beim Abschneiden einer (1) von ihnen entsteht (Abb.14a, 1. Teilbild).
Ebenso leicht vorhersagbar ist, dass ein 6-Eck entsteht, nämlich beim Schneiden durch den Mittelteil des Körpers (5. Teilbild). Dieser ist von 6 der insgesamt 30 Kanten umgeben (Abb.8, rechts).
Ein 6-Eck entsteht auch beim gemeinsamen Abschneiden von 4 (3. Teilbild) oder 6 Ecken (Abb.14b, 2. Teilbild).
Ein 4-Eck entsteht, wenn unter einer (1) der Kanten geschnitten wird (gemeinsames Abschneiden von 2 Körperecken, Abb.14a, 2. Teilbild). 2 der von den beiden Körperecken ausgehenden insgesamt 6 Kanten sind die gemeinsame Kante, die mit weggeschnitten wird. Der Schnitt führt nur durch 4 Kanten, und die Schnittfigur ist ein 4-Eck.
Werden 3 Körperecken gemeinsam weggeschnitten, so entfallen auch 2 Kanten. Von insgesamt 9 der von den 3 Körperecken weglaufenden Kanten werden 4 (2 mal 2) gemeinsam gebraucht und mit weggeschnitten. Der Schnitt führt nur durch 5 Kanten, und die Schnittfigur ist ein 5-Eck (Abb.14b, 1. Teilbild).
Das 8-Eck ist diejenige mögliche Schnittfigur, die die meisten Ecken enthält (Abb.14a, 4. Teilbild und Abb.14b, 3. Teilbild). Dabei werden je 2 Körperkanten ziemlich schleifend geschnitten (die dadurch verursachten schwachen Knicke in den Schnittfiguren sind in den Teilbildern mit je einem roten Punkt markiert).
4.5 Antiprismen ↑ Anfang
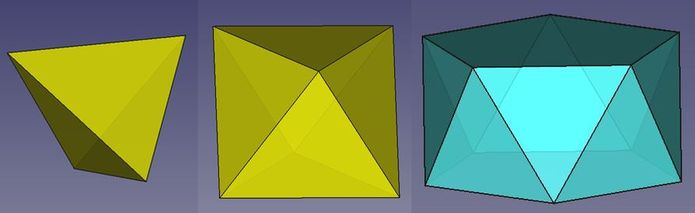 Abb.15 uniforme Antiprismen
Abb.15 uniforme Antiprismen
Tetraeder - Oktaeder - mittlerer Teil des
Ikosaeders
In der Legende von Abb.8 ist die Eigenschaft des mittleren Teiles eines Ikosaeders als uniformes Antiprisma bereits erwähnt. Uniforme Antiprismen sind aber auch Oktaeder und Tetraeder, jeweils als Ganzes. Das Tetraeder ist ein Grenzfall eines Antiprismas, denn es hat als Grund- und Deckfläche lediglich eine Linie. Der entsprechende Grenzfall eines Prismas - Grund- und Decklinie sind nicht gegeneinander verdreht (die verbindenden Flächen sind eben, müssen nicht in Dreiecke aufgelöst werden) - ist eine Ebene anstatt ein Körper.
5. Literatur ↑ Anfang
[1] Platon: "Timaios".
[2] Euklid: ''Die Elemente'', Buch XIII, § 18a.
[3] Max Bill: Zwei gleiche Würfel-Hälften aus der Serie "schtatt e schtadt e schtatt"
schrift-deutsch: anstatt einer Stadt eine Statt [Stätte];
prononcierter: anstatt eine ganze Stadt nur ein Platz ["darauf eine Plasik von mir, Max Bill"]
aus "Die Liebe zur Geometrie", du, Heft 10, Oktober 1988
![]() Siegfried Wetzel, CH 3400 Burgdorf, Dezember 2017
Siegfried Wetzel, CH 3400 Burgdorf, Dezember 2017
↑↑ Anfang
<< Home
<< anderes Geometrisches