<< Home
<< anderes Geometrisches
 ↓↓ Ende

Dichteste Kugelpackung

Inhalt

  1. Einleitung
  2. Schichtweises Errichten von Pyramiden aus Kanonen- oder anderen Kugeln
  3. Die unterste Schicht der Kugelpyramiden
  4. Die drei untersten Schichten der Kugelpyramiden
      4.1 Die Packungsdichte der vierseitigen Pyramide
      4.2 Die Packungsdichte der dreiseitigen Pyramide
  5. Vergleich zwischen den bei den beiden Kugelpyramiden angewendeten Packungen
      5.1 Durch Umlegen der Schichten einer dreiseitigen Pyramide entsteht eine vierseitige Pyramide
      5.2 Schichten mit quadratischem Muster im Inneren einer dreiseitigen Pyramide
  6. Die kubisch-flächenzentrierte Elementarzelle
  7. Die hexagonale Elementarzelle
  8. Die kristallographischen Elementarzellen und ihre Packungsdichten
      8.1 Die Packungsdichte der kubisch-flächenzentrierten Elementarzelle
      8.2 Die Packungsdichte der hexagonalen Elementarzelle
  9. ABA und ABCA — in der Krisrallographie gebrauchte Kürzel beim Stapeln hexagonaler Kugelschichten
      9.1 Die ABA-Stapelfolge
      9.2 Die ABCA-Stapelfolge
      9.3 Quadratisch gemusterte Kugelschichten
10. Kugelpyramiden-Varianten
     10.1 Dreiseitige Kugelpyramiden
     10.2 Die vierseitige Kugelpyramide
     10.3 Eine sechseitige Kugelpyramide
     10.4 Eine aus hexagonalen Elementarzellen bestehende Kugelpyramide
11. Literatur

1. Einleitung   ↑ Anfang

Bei auf Burgen noch vorhandenen alten Kanonen oder in älteren Festungen werden oft auch in Haufen geschichtete Kanonenkugeln aufbewahrt. Solche Kugelhaufen haben manchmal die Kontur einer dreiseitigen Pyramide (Abb.1, vorne). Meistens sehen sie aus wie vierseitige Pyramiden oder wie Walmdächer (Abb.1, hinten und links). In der dreiseitigen Pyramide scheinen die Kugeln am dichtesten gepackt zu sein. Der Schein trügt aber: Die Packungsdichte ist in beiden Pyramiden gleich, wobei es sich um die dichteste Packung handelt, die mit Kugeln möglich ist. Der Anteil ihres eigenen Volumens ist 74,048 % des von ihnen beanspruchten Raumes. Der Leerraum zwischen ihnen ist mit etwa 26% etwa ein Drittel ihres eigenen Volumens.

Es handelt sich um einen Grenzwert für aus unendlich vielen Kugeln bestehende Packungen. Bei endlich großen Kugelhaufen gilt er auch (Grenzwertbetrachtung nicht erforderlich), wenn man ihre Hülle durch die Mittelpunkte der sie begrenzenden Kugeln legt.

<< Abb.1  In einem kolonialzeitlichen Fort gestapelte
                Kanonenkugeln;
                eine dreiseitige Pyramiden- und
                zwei besonders lange Walmdach-Packungen
                [1, Seite 3, Abbildung 2 (a)]

Der Wert der größten Packungsdichte wird im Folgenden hergeleitet, wobei stets beide o.g. Pyramidenformen (Abb.1 u. Abb.2) in vergleichende Betrachtungen einbezogen werden. Den Versuch, mich ausschließlich an Kanonenkugelpackungen — bzw. weil ich kein Burgherr sondern eher Pazifist bin — an z.B. aus Holz gefertigte Spielzeugkugeln zu halten, gab ich bald auf. Die Packungsdichte inkl. der bestmöglichen ist ein vorwiegend in der Kristallographie gebrauchter und ein dort allgemein entwickelter Begriff. Zudem sind dort weitere Zusammenhänge erforscht, die auch beim Packen von Holzkugeln nützlich anwendbar sind, so dass ich einen etwas längeren Ausflug in die Kristallographie unternehmen werde.

Abb.2  Zwei Kugelpyramiden; links Kanonen- (quadratische Basis), rechts Holzkugeln (gleichseitige Dreieck-Basis)
           [2, Abb.8]

2. Schichtweises Errichten von Pyramiden aus Kanonen- oder anderen Kugeln
    ↑ Anfang

Es ist naheliegend, dass kompakte Packungen aus einzelnen ebenen, mit Kugeln belegten Schichten bestehen, und dass sich in den Packungen parallele und in mehreren Richtungen orientierte Kugelebenen bezeichnen lassen. Dabei ist keine Richtung bevorzugt. Es ist lediglich praktisch, dass ein Haufen aus Kanonenkugeln oder anderen Kugeln schichtweise vom Boden ausgehend erstellt wird. Und es spricht nichts dagegen, die horizontale Schichtung zur Basis allgemeiner Betrachtungen zu erklären.

3. Die unterste Schicht der Kugelpyramiden  ↑ Anfang

Die Lücken in der untersten Schicht der vierseitigen Pyramide sind größer als die in der dreiseitigen. In Letzterer sind die Kugeln enger zusammen gerückt. Jede von ihnen berührt 6 Nachbarkugeln (Abb.3-rechts). In der Ersten berührt jede Kugel nur 4 Nachbarn (Abb.3-links). In der Mittenebene (enthält die Kugelmittelpunkte) dieser Schicht bleiben 21 % der Fläche leer, während es bei der zur dreiseitgen Pyramide gehörenden Schicht nur 9,3 % sind. Diese Zahlen haben aber keine direkte Bedeutung, weil die gesuchte Packungsdichte eine das Volumen betreffende Verhältniszahl ist. Sie sind aber der Grund für die oben genannte Täuschung, dass die vierseitige Pyramide eine kleinere Packungsdichte hätte.

Abb.3  Jeweilige unterste Schicht der Pyramiden aus Abb.12; links: CAD-Modell; rechts: Holzkugeln

Dass Kanonnenkugeln bevorzugt auf quadratischem oder allgemein rechteckigem Grundriss gestapelt wurden, ist vermutlich einem allgemeinen Hang zum rechten Winkel geschuldet. Durch Probieren wäre leicht herauszufinden gewesen, dass auch das regelmäßige Dreieck oder Vielfache davon (z.B. Raute und Sechseck) geeignet, ungerade Umrandungen (z.B. Kreis, Ellipse) aber eher ungeeignet sind. Damit die Kanonenkugeln nicht wegrollen, wurden sie von einem Rahmen umgeben oder in Boden-Dellen gelegt. Als die Burgen inklusive ihrer alten Waffen öffentlich zugänglich wurden, hat man sie –zumindest die äußeren Kugeln– aneinander geschweißt, damit keine Kugel "verloren gehen" kann. Der Rahmen verlor in diesem Moment seine Aufgabe.

4. Die drei untersten Schichten der Kugelpyramiden  ↑ Anfang

Eine Kugel, die man auf eine der beiden Bodenschichten legt, fällt von selbst in eine der zwischen vier (vierseitige P.) bzw. drei (dreiseitige P.) Bodenkugeln bestehende Lücken hinein. Mit weiteren Kugeln entsteht eine weitere Schicht mit gleichem Muster wie in der Bodenschicht. Nur die Randreihen sind um je eine Kugel kürzer. Sie liegen um einen halben Kugeldurchmesser gegen die Randreihe darunter versetzt. Da die Schichten der dreiseitigen Pyramide doppelt so viele Lücken wie Kugeln haben (aber nur jede zweite Lücke besetzt werden kann), hat man prinzipiell die Wahl, mit welcher Lücke man anfängt. Bei der hier zur Debatte stehende Pyramide (Abb.2-rechts), hat man immer die randnächsten Lücken besetzt und dadurch eine steilwandige und bei gegebener Grundfläche die größt mögliche Höhe erreicht.

Nach dem Auflegen der dritten Kugelschicht sind die Lücken der zweiten Schicht allseitig begrenzt, so dass in ihr die in allen Schichten gültige Packungsdichte untersucht werden kann.

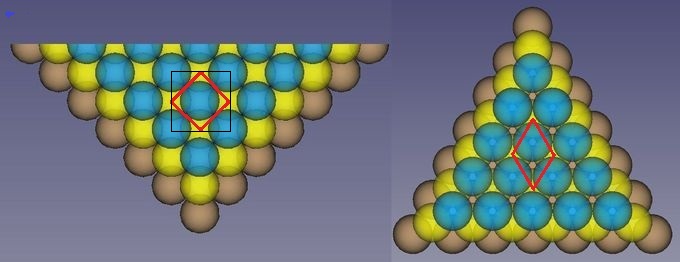
Abb.4  Drei unterste Schichten der Pyramiden aus Abb.2 (hier links: vierseitige Pyramide ist halbiert); CAD-Modelle.
           Die Kugeln der beiden oberen Schichten sind teildurchsichtig, so dass ihre zentrische Lage in den darunter
           befindlichen Lücken erkennbar bleibt.

Herauszufinden sind Form und Volumen einer kleinsten Zelle, die von Teilen der eine Lücke umgebenden Kugeln begrenzt wird. Als Packunsdichte ergibt sich das Verhältnis zwischen der Differenz zwischen Zellenvolumen und Lückenvolumen und dem Zellenvolumen.

Es zeigt sich, dass mit quaderförmigen Zellen (ebene Boden- und Deckfläche) gearbeitet werden kann, indem man die ineinander "verzahnten" Kugelschichten "glättet". Die "Zähne" sind Teile (Kalotten) der von unten und oben in die Lücken hinenragenden Kugeln. Je eine Hälfte dieser Kalotten wird einer der benachbarten Schichten zugerechnet. Man gewinnt ebene "Stammschichten", die etwas weniger dick als der Durchmesser einer Kugel sind, und die aus quaderförmigen "Stammzellen" bestehen.

4.1  Die Packungsdichte der vierseitigen Pyramide   ↑ Anfang

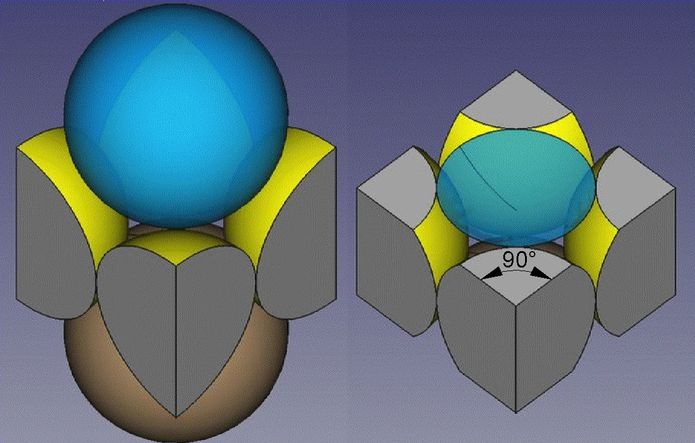
Abb.5  Quadratische Stammzelle; links: vertikal beschnitten; rechts: zusätzlich horizontal beschnitten

Die Stammzelle in den Schichten der vierseitigen Pyramide hat quadratischen Querschnitt (Abb.3-links). Ihre vertikalen Kanten führen durch die Mittelpunkte der vier die Lücke bildenden Kugeln (Abb.4-rechts). Je ein Viertel dieser Kugeln (in der Summe 1 ganze Kugel) liegt innerhalb der Zelle. Es ist leicht erkennbar, dass die von den oben und unten hineinragenden Kugeln abgetrennten Kalotten im Volumen gleich sind wie die jeweils vier oben und unten von den begrenzenden Kugelvierteln abgetrennten Spitzen. Anders gesagt: Vier Spitzen bilden zusammen ebenfalls und eine gleich große (kopfüber positionierte) Kalotte. Der Wegschnitt der Spitzen wird von der jeweiligen in der Lücke verbleibenden Kalotte der hineingefallenen Kugel kompensiert. Wegen der Gleichheit zwischen "verlorenem" und "gewonnenem" Volumen ist das in einer Stammzelle enthaltene Kugelvolumen genau so groß wie das einer ganzen "unversehrten" Kugel. Die Rechenarbeit für die Ermittlung der Packungsdichte wird folglich stark gemindert.

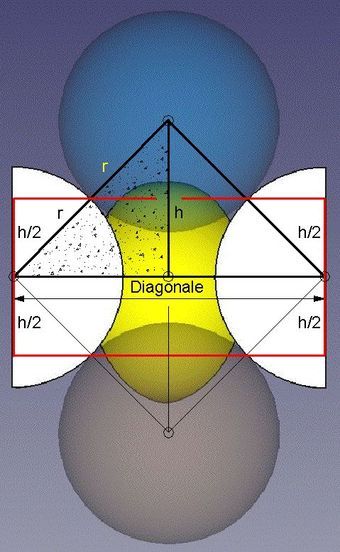<< Abb.6  Quadratische Stammzelle (Diagonalschnitt):
                mit Skizze für die Berechnung

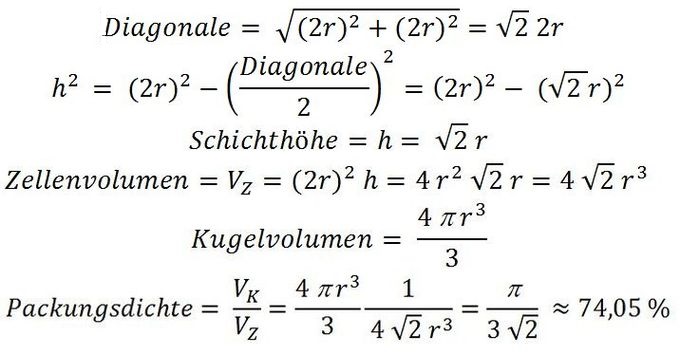↑↑ Abb.7  Quadratische Stammzelle:
                Berechnung der Packungsdichte

Die Rechnung ist sogar ziemlich kurz, denn die noch zu ermittelnde Dicke h der Stammschicht bzw. der Höhe der Stammzelle ist der Zeichnung (Abb.5) schon anzusehen: h = √2·r.
Die entsprechende Berechnung erfolgt dennoch (Abb.6). Sie geht davon aus, dass die Stammzelle quadratischen Querschnitt mit Kantenlänge 2·r hat, und die Diagonale somit √2·2·r ist.
Das Dreieck, das die anschließend gebrauchten geometrischen Beziehungen (Satz des Pythagoras und Strahlensatz) visualisiert, ist mit einer Rasterfüllung gekennzeichnet.

Der Quotient aus Kugelvolumen V_K und Zellenvolumen V_Z ist der gesuchte Wert der Packungsdichte: ≈ 74,05 % .

4.2  Die Packungsdichte der dreiseitigen Pyramide   ↑ Anfang

Hier hat die Stammzelle rautenförmigen Querschnitt (siehe Abb.4-rechts). Sie enthält ebenfalls vier Kugelteile (zwei
Kugel-Sechstel und zwei Kugel-Drittel), die zusammen wieder eine ganze Kugel ausmachen. Anstatt nur einer von vier Kugelvierteln gebildeten Lücke enthält sie zwei kleinere, jeweils von drei Teil-Kugeln gebildete Lücken. Die Lücken liegen näher beisammen, so dass nicht in beide Kugeln hineinfallen können. In die eine fällt eine von oben, und in die andere ragt eine von unten hinein (beides weiniger tief als bei der vierseitigen Pyramide). Die Stammschicht ist somit dicker, und die Kalotten sind kleiner.

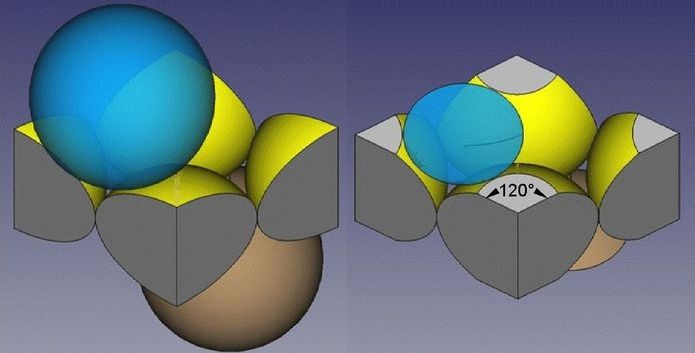Abb.8  Rautenförmige Stammzelle; links: vertikal beschnitten; rechts: zusätzlich horizontal beschnitten
           (in der Draufsicht gegenüber Abb.4/rechts um 90° gedreht)

Auch hier ist leicht erkennbar, dass das Volumen der von den beiden Kugeln verbleibenden Kalotten gleich groß wie das zusammen gezählte Volumen der von den vier die Lücke bildenden Kugel-Teilen abgetrennten acht Spitzen ist. Die Rechenarbeit (Abb.10) für die Ermittlung der Packungsdichte ist etwas länger, aber gleich einfach wie bei der vierseitigen Pyramide.

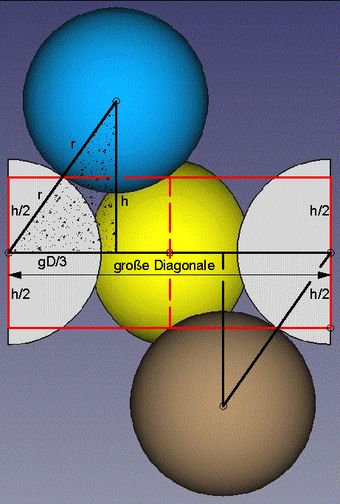<< Abb.9  Rautenförmige Stammzelle
                (großer Diagonalschnitt):
                mit Skizze für die Berechnung

↑ ↑ Abb.10  Rautenförmige Stammzelle
                 Berechnung der Packungsdichte

Das Volumen der rautenförmigen Stammzelle ist gleich groß wie das der quadratischen. Folglich hat sich der Quotient aus Kugelvolumen V_K und Zellenvolumen V_Z nicht geändert. Die Packungsdichte ist gleich wie in der vierseitigen Pyramide, nämlich ≈ 74,05 % .

Der Vergleich der Rechnungen (Abb.10 mit Abb.89) zeigt, dass die Stammschicht in gleichem Maße dicker wie ihre Grundfläche kleiner geworden ist. Das Verhälnis der Dicken h_Quad / h_Raute ist √3 /2, und das der Grundflächen
F_Quad / F_Raute ist 2 /√3.

5. Vergleich zwischen den bei den Kugelpyramiden angewendeten Packungen
    ↑ Anfang

Da die vierseitige und die dreiseitige Pyramide die gleiche (mit etwa 74 % die dichteste) Kugelpackung haben, verblüfft wegen ihrer äußerer Verschiedenheit. Sind sie nur scheinbar verschieden? Verschwindet ihr verschiedenes Erscheinen, wenn man sie in gleicher Weise betrachtet? Wie wäre diese gleiche Weise zu formulieren?

Bei genauerem Hinsehen stellt man fest, dass die Seitenwände beider Pyramiden das gleiche hexagonale Muster
(6 Kugeln umschließen eng eine 7. Kugel, Abb.2) aufweisen. Das heißt, dass auch bei der vierseitigen Pyramide dieses schon in der Grundschicht der dreiseitigen Pyramide vorhandene Muster (Abb.3-rechts) auftritt. Und, es stellt sich sofort die Frage nach dem Umgekehrten: Tritt das quadratische Muster, wenn schon nicht in den sichtbaren Wänden der dreiseitigen Pyramide, so doch in ihrem Inneren auf?

5.1  Durch Umlegen der Schichten einer dreiseitigen Pyramide entsteht eine
       vierseitige Pyramide   ↑ Anfang

Diese Feststellung und die Kenntnis davon, dass man Schichten mit hexagonalem Muster auf zweierlei Weise aufeinanderlegen kann (s. Abschnitt 4., erster Absatz), gaben Anlass, das Modell der dreiseitigen Pyramide (Abb. 2-rechts und Abb.11-links) einmal anders zu schichten: Die Schichten waren untereinander nicht verleimt, sodass sie anders aufeinander gelegt werden konnten. In der Variante (Abb.11-rechts; schiefe Pyramide) ist das zweite mögliche Aufeinanderlegen angewendet: nicht in die randnächsten, sondern in die weiter entfernten Lücken, wobei kein seitlicher Versatz gegenüber der jeweils darunter liegenden Schicht entstand.
Ergebnis:
Die überhängende Seite ist hexagonal gemustert geblieben. Aber die beiden anderen Seiten haben quadratisches Muster bekommen. Sie sind also gleich wie die Bodenschicht der vierseitigen Pyramide (Abb.3-links) gemustert.

Abb.11  Schichten der Dreierpyramide verschieden aufeinander gelegt
             links: Standard; rechts: Folgeschicht jeweils leicht nach rechts und nach hinten verschoben

Da nun eine Packung vorlag, die auch quadratisch gemusterten Flächen enthielt, war es naheliegend, eine davon zur Bodenschicht zu machen (Abb.12; die wieder verwendeten Schichten wurden zusammen geleimt).
Ergebnis: Aus der ehemals dreiseitigen Pyramide (Abb.2-rechts) ist eine halbe vierseitige Pyramide (Abb.2-links) geworden (da die mittlere vertikale Schicht nicht halbiert wurde, macht sie etwas mehr als eine halbe vierseitige Pyramide aus).
Zusätzliches Ergebnis: Eine vierseitige Pyramide enthält nicht nur horizontale sondern auch vertikale quadratisch gemusterte Schichten. Diese treten im Inneren auf und haben die Richtung der Pyramidendiagonalen (Abb. 12-rechts).
Nebenbemerkung:
Dass diese Pyramide im Inneren auch hexagonale Schichten hat, ist schon bekannt, denn die von außen sichtbaren Schichten (hier auf den vier Wänden) setzen sich als Parallele ins Innere fort. Das gilt allgemein: Die hexagonalen Seitenwand-Schichten der dreiseitigen Pyramide setzen sich dort auch parallel ins Innere fort.

Abb.12  auf eine neue Seitenfläche gelegte Dreierpyramide (Abb.11-rechts: gegeneinander verschobene Schichten)
             mit dem Ergebnis einer halben Viererpyramide
             links: Blick von vorn; rechts: Blick von hinten (auf Pyramidendiagonale)

5.2  Schichten mit quadratischem Muster im Inneren einer dreiseitigen Pyramide   ↑ Anfang

Die vierseitige Pyramide zeigt beide Legemuster auf den sie begrenzenden Oberflächen (Boden und Wände). Beim oben besprochenen Umlegeexperiment wurde sichtbar, dass quadratische Schichtmuster nicht nur horizontal, sondern auch vertikal in ihr existieren.

In obigem Umlegeexperiment entstand eine dreiseitige Pyramide mit quadratischem Legemuster auf den Wänden (und selbstverständlich zu diesen parallel auch im Innern). Aber besonders wichtig daran war, dass eine Spur zu einer grundlegenden Erscheinung, nämlich der dichtesten Anordnung der Kugeln in einem kubisch-flächenzentrierten Gitter gelegt wurde. Dieser wird im Folgenden in kleinen Schritten nachgegangen.

Vorschau: In der Kristallographie wird die dichteste Kugelpackung vorwiegend mit den vorliegenden Gitterformen (neben der kubisch-flächenzentrierten gibt es noch die hexagonale Elementarzelle) und nicht mit den Mustern der Kugelschichten beschrieben.

Der Flächenwinkel zwischen den beiden nicht-überhängenden Seiten der neu geschichteten Pyramide ist 90°.
(Man erkennt das in Abb.12: Die Pyramide bzw. die neu zusammengesetzte Kugelpackung liegt waagerecht auf einer dieser Seiten, während sich die andere senkrecht erhebt.)

Trennt man den überhängenden Teil ab, erhält man eine regelmäßige dreiseitige Pyramide, die wesentlich weniger steil und viel niedriger als die Ausgangspyramide ist (angedeutet in Abb.11-rechts: Spitzen-Kugel über 3 Schichten, vorher über 6 Schichten).
Die Seiten bilden an der gekappten Pyramiden-Spitze je ein rechtwinkliges Dreieck.
Auch über den beiden anderen schrägen Kanten dieser gekappten Pyramide sind die Flächenwinkel 90°.

Der mehrfach auftretende Winkel zeigt, dass die gekappte dreiseitige Pyramide ein Eckstück eines Würfels (Hexaeder) ist. Die Kombination der dichtest gepackten Kugeln zu Würfeln (kubisch-flächenzentriertes Gitter) im Inneren solcher Kugelhaufen gilt es herauszustellen. Als beispielhafter Kugelhaufen wird die Standard-Dreiseiten-Pyramide benutzt.

Während der derzeitigen Corona-Krise (April 2020) kann ich keine Holz- oder anderer Kugeln nachkaufen, so dass mir keine weiteren Experimente mit anfassbaren Kugeln möglich sind. Ich stelle im Folgenden auf virtuelle Modelle um.

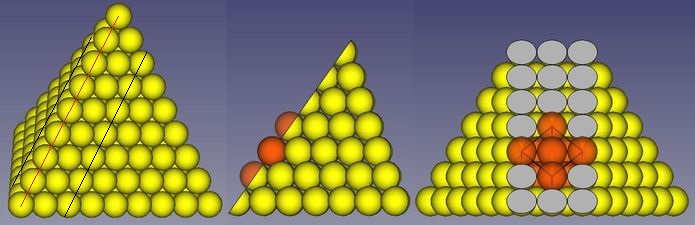Abb.13  Kanten-paralleler Schnitt durch eine Standard-Dreierpyramide
             links; Dreierpyramide (siehe auch Abb. 2-rechts und Abb.11-links)
             Mitte: linke Kante abgeschnitten
             rechts: Blick auf die Schnittfläche der Rest-Pyramide
                 Vorschau: Aus der Schnittfläche ragen ein paar ungeschnittene, rot markierte Kugeln hervor. Es handelt sich um 5 von 14 Kugeln,
                 die an der kubisch-flächenzentrierten Kristallzelle, die weiter unten behandelt wird, beteiligt sind.

Um Schichten in einer Pyramide mit anderen als den Mustern auf den Oberflächen erkennen zu können, ist sie nicht-parallel zu einer Oberfläche zu durchschneiden. Dabei bietet sich ein zu den Kanten paralleler Schnitt durch die beiden ihr benachbarten Flächen an. In Abb.13 führt der Schnitt durch die jeweils dritte von der linken Kante (rote Linie) entfernte, auf den angrenzenden Flächen befindlichen Kugelreihe (schwarze Linien) hindurch. Nach Wegnahme der Kanten-nahen und der durch den Schnitt entstandenen halben Kugeln ist auf der Rest-Pyramide das von der Viererpyramide bekannte quadratische Muster sichtbar (rechts in Abb.13).

<< Abb.14  Kugelwürfel       [2, Abb.9]

Nachdem an den beiden anderen Kanten der gleiche Schnitt erfolgte, ist die Ecke eines Würfels (Hexaeder) erkennbar. Von der dreiseitigen Pyramide bleibt ein ganzer Würfel übrig, wenn man die unteren Teile, die noch an die Pyramide erinnern, durch parallel zu den bisher geführten Schnitten abtrennt.

Auf diese Weise könnte der Kugelwürfel, den ich einmal früher anfertigte, entstanden sein (Abb.14). Die Dreierpyramide hätte wesentlich größer sein müssen als die oben benutzte, damit der gefundene relativ große Kugelwürfel in ihr enthalten gewesen wäre. Da die Randkugeln ungeteilt blieben, wären nicht ebene Schnitte möglich gewesen, sondern man hätte die mit den verbliebenen "verzahnt" verbundenen Kugeln weggenommen.
Tatsächlich leimte ich diesen Würfel aus dreieckigen Schichten mit hexagonalem Muster zusammen. Die Schicht am Anfang des oberen Würfeldrittels ist gelb markiert.

Das wie erwartet gefundene quadratische Schichten-Muster ist inzwischen Nebensache geworden. Der Makro-Würfel von Abb.14 lenkt das Augenmerk jetzt auf die kubische Elementarzelle.

6. Die kubisch-flächenzentrierte Elementarzelle   ↑ Anfang

Bei der Beschäftigung mit der dichtesten Kugelpackung ist an der Kristallographie nicht vorbeizukommen. Sie spielt bei der Beschreibung der Volumen-minimierten Zusammensetzung der Materie aus ihren kleinsten Teilchen (Atome, Moleküle u. a.) eine wichtigere und bleibendere Rolle als bei den Kanonenkugeln. Die Methoden zur Beschreibung eines solchen geometrischen Problems im dreidimensionalen Raum wurden erst vom Fachgebiet Kristallographie relativ umfassend erarbeitet. Sie sind allgemein — so auch für Kanonenkugeln und Spielkugeln — anwendbar, obwohl sie aus der Kristallographie heraus wegen der Kleinheit derer Objekte nicht besonders anschaulich vermittelbar sind. Bei den kleinsten Teilen der Materie muss man zudem Annahmen über deren Gestalt machen. Man kennt diese gar nicht umfassend genau. So ist die kugelförmige Hülle der Atome lediglich eine — für den Zweck der Untersuchungen aber ausreichende — Annahme.

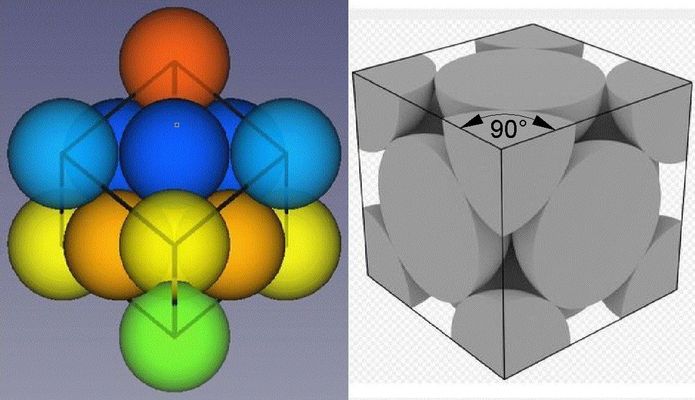Abb.15  kubisch-flächenzentrierte Elementarzelle
             links: aus dreiseitiger Pyramide herausgearbeitet (siehe Abb.13)
             rechts: Kristallographie-übliche Darstellung (Wikipedia)

Die in Abb.13 schon markierte (rot) kubisch-flächenzentrierte Kugelkombination ist in Abb.15-links noch einmal (vergrößert und farbig verschieden markiert) gezeigt. Der Kubus (Gitter) steht auf einer Spitze. Seine vertikale Raumdiagonale erstreckt sich durch vier Kugelschichten. Die aus den mittleren der vier Schichten stammenden zwei mal sechs Kugegeln haben je die gleiche, aber verschieden helle Farbe. Die jeweils helleren Kugeln sitzen auf den Ecken des Kubus, die dunkleren auf seinen Flächen. Die obere und die untere Kugel ergänzen die Eckkugeln auf insgesamt acht Stück.

Rechts in Abb.15 ist die Kristallographie-übliche Darstellung der kubisch-flächenzentrierten Kombination der kleinsten Materieteilchen gezeigt. Man stellt sich den Aufbau der Materie zu relativ gegenüber ihren kleinsten Teilchen riesengroßen Kristallen aus elementaren Bauteilen vor. In diesen sind einige kleinste Teilchen (14 im kubisch-flächenzentrierten) zusammengefasst. Das Gerüst (Gitter) dieser Bauteile hat die Form eines der geometrischen Körper, die zusammengelegt den Raum lückenlos füllen ("Parkett", räumlich). Die an den Ecken und in den Flächen sitzenden kleinsten Teilchen (in möglicherweise aüßerer Gestalt von Kugeln) werden soweit beschnitten, dass nur noch der jeweils im Gitterinneren sich befindende Anteile übrig bleiben. Das Abgeschnittene geht nicht verloren, es ist restlos aufgeteilt auf die im Kristall jeweils zusammenstoßenden Kristalle (beim kubisch-flächenzentrierten: je acht Eckenanstößer und je zwei Flächenanstößer). Die Kristallbausteine sind glattwandige, Elementarzellen genannte Gebilde. Das kubisch-flächenzentrierte Gebilde ist die kubisch-flächenzentrierte Elementarzelle (Abkürzung f. c. c = face centered cubic)

Man könnte überrascht sein, diese Kombination aus Kugeln in einer Pyramide zu finden, die aus hexagonal gemusterten Kugelschichten zusammengestellt wurde. Bei einer Pyramide aus quadratisch gemusterten Schichten wäre es viel naheliegender, einen solchen Fund zu machen. Man muss aber bedenken, dass die Natur der Materie mit in horizontalen Schichten augehäuften Kanonenkugeln nicht viel zu tun hat. Die Kristalle sind riesenzählige Teilchenanhäufungen, bei denen die horizontale oder irgendeine Vorzugslage irrelevant ist.

<< Abb.16  Zwei gleiche Würfel-Hälften von Max Bill   [3]
                  aus der Serie "schtatt e schtadt e schtatt"

Die Überraschung tritt in den Hintergrund, wenn man sich erinnert, oder von einem Künstler daran erinnert wird (Abb.16), dass es sechseckige Würfelschnitte gibt. Beim zur Raumdiagonalen rechtwinkligen und diese halbierenden Schnitt ensteht sogar ein regelmäßiges Sechseck, das die hexagonal gemusterte Kugelschicht kennzeichnet. Deutlicher zutage tritt in der kubisch-flächenzentrierten Zelle der Bezug auf das darin enthaltene kleinteiligere regelmäßige Dreieck-Muster. Von den beteiligten beiden mittleren Schichten besetzen je drei Kugeln Würfelecken und je drei Kugeln Würfelflächen. Sie besetzen die Ecken gleichseitiger Dreiecke (das der Eckkugeln ist in Abb.16-links nachgezeichnet).

Nebenbemerkung: Das in Abb.16 nachgezeichnete Dreieck begrenzt auch den Boden der gekappten dreiseitigen Kugelpyramide von Abb.11-rechts (ebenfalls nachgezeichnet).

7. Die hexagonale Elementarzelle   ↑ Anfang

Es gibt nicht nur die hexagonal gemusterte Kugelschicht und die darin zu findende kubische Elementarzelle, sondern doch auch die sogenannte hexagonale Elementarzelle (Abkürzung h. c. c = hexagonal centered cell). Bei den Metallen ist sie sogar etwas häufiger als die kubische [4]. Der Unterschied zwischen den beiden Zellentypen ist nicht die Hexagonalität in den Kugelschichten, sondern beruht darauf, dass die Schichten aus kleinsten Teilchen der Materie auf zweierlei Weise aufeinander gestapelt sind. Die kubische Zelle erstreckt sich über vier Schichten, von denen erst die dritt-folgende fluchtend über der ersten liegt. Die hexagonale Zelle erstreckt sich auch über mehrere Schichten (über drei), wobei aber bereits die zweit-folgende über der ersten liegt. Andere Stapelreihenfolgen kommen in der Natur kaum vor, obwohl prinzipiell (unendliche Ausdehnung der Materie unterstellt) unendlich viele Stapelfolgen möglich sind. Einzige Einschränkung ist: Die erst-folgende Schicht kann wegen des Einrastens in die Lücken in der Schicht darunter nicht fluchtend über dieser liegen. Dass es überhaupt zu Unterschieden kommen kann, liegt daran, dass es zwei mögliche Stellen zum Einrasten gibt (formal 6, was sich aber wegen der diesbezüglich 3-fachen Symmetrie in der Schichtebene rund um eine Kugel auf praktisch nur 2 reduziert). In der Kristallographie werden die beiden allein bedeutsamen Stapelfolgen mit den Kürzeln ABAB... (hexagonale Zelle) und ABCABC... (kubische Zelle) angegeben.

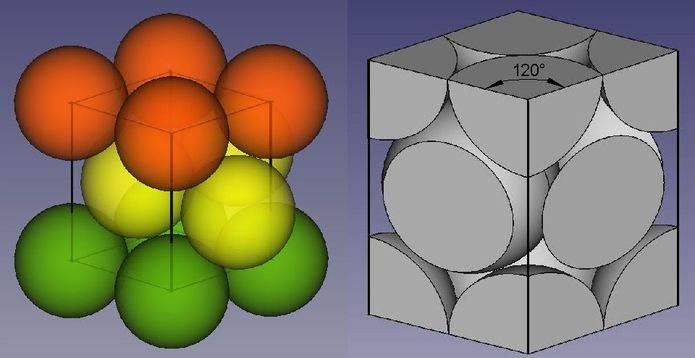Abb.17  hexagonale Elementarzelle
             links: aus drei hexagonalen Kugelschichten herausgearbeitet
             rechts: Kristallographie-konsequente Darstellung

Eine mit massiven Kugeln gefüllte hexagonale Elementarzelle ist ein "Unding". Sie enthält zwar genau die Volumenmenge einer ganzen Kugel, beherbergt diese aber in drei Teile zerschnitten. Der Grund dafür ist, dass die Kugel nicht in der Mitte des rautenförmigen Mantels dieses Quaders sitzt. Die kleineren Kugelteile (Kalotten) gehören formal zu zwei Nachbarzellen, die beim Parkettieren des Raums rundum angefügt werden und dort zu "heilen" Kugeln führen. Zwei weitere Nachbarn "liefern" je eine Kalotte, mit denen der große Kugelrest in der beschnittenen Ausgangszelle wieder zu einer ganzen Kugel ergänzt wird. In der Kristallographie stört das, was ich als Unding empfinde, überhaupt nicht, denn die Bezeichnung des z.B. riesigen leeren Raums um den Atomkern herum, in dem sich ein paar Elekrtronen aufhalten, als Kugel ist lediglich eine für die nützliche Beschreibung der Materie gebrauchte Analogie. Meistens werden sogar kleine Kugeln oder nur Punkte in die Zelle eingezeichnet (Abb.18,links). Bei diesem Brauch ragt dann nichts über den Rand der Zelle hinaus. Die Nützlichkeit der Kristallographie hängt nicht vom Gebrauch ästhetisch ansprechender Objekte in den Bildern ab.
Es gibt allerdings auch hier wie in jedem Fachgebiet Ungereimtheiten. Eine davon ist der Name Hexagonale Elementarzelle, die gar kein hexagonal geformter Körper ist. Man hat offensichtlich zuerst mit der "echten" hexagonalen Zelle gearbeitet und ein Drittel davon erst später zur nicht mehr verkleinerbaren rautenförmigen (120° stumpfer Innenwinkel) Elementarzelle erklärt. Am Problem des Hinausragens über den Zellenrand änderte das nichts; vorher waren drei innere Kugeln betroffen, danach eine. Der beibehaltene Namen irritiert den außenstehende Interessent. Aufklärung darüber ist nicht zu finen (ich habe allerdings auch nur Enzyklopädien und keine Lehrbücher gelesen).

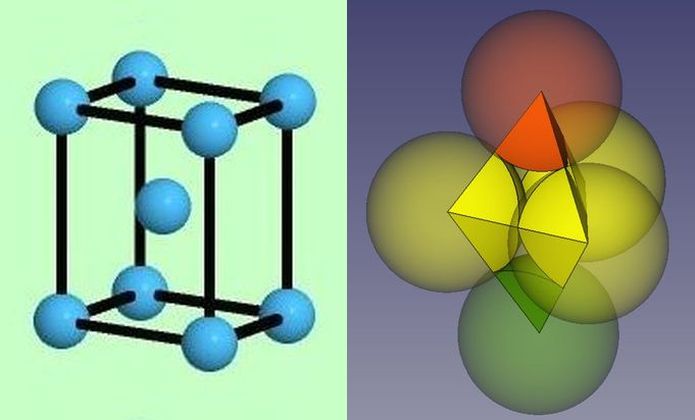Abb.18  hexagonale Kugelzellen
             links: in Chemie/Kristallographie bevorzugte Darstellung der Elementarzelle mit kleinen, die Zelle nicht
             füllenden Kugeln (häufig noch kleiner als im vorliegenden Bild)    [5]
             rechts: Entwurf einer ästhetisch ansprechenderen Zelle mit ausschließlich zentrisch geschnittenen Kugeln

Noch eine Bemerkung zu meinem Empfinden der hexagonalen Zelle als "Unding":
Ich werde diesen Artikel neben andere Artikel unter dem Stichwort Geometrisches einordnen, in denen es um "Platonische Gegenstände", ..., die man lieben kann, ohne dass sie einem zudienen, geht. Sie dienen mir nur ausnahmsweise zur Erklärung eines natürlichen Zusammenhangs. Das ist jetzt der Fall bei den Kugelpackungen, von denen ich bisher nur Arrangements erstellte [2, Abb.n 8 u. 9]. Nun interessiert mich die natürliche Erscheinung, dass die Packungsdichte von Kugeln einen Grenzwert besitzt. Von der Kristallographie, die diesen Zusammenhang inkl. des Grenzwertes der dichtesten Kugelpackung seit langem kennt, erfuhr ich von zwei Elementarzellen,in denen dichtest gepackte Kugeln zusammengefasst werden. Die eine, nämlich die kubisch-flächenzentrierte nehme ich als ästhetisch sehr schönes Kugelarrangement wahr, während mich die hexagonale gar nicht anspricht. Diese Abneigung regte mich an, etwas Ansprechenderes zu suchen. Gefunden habe ich die in Abb.18-rechts dargestellte Minizelle (mini, weil die Addition der darin enthaltenen Kugelteile nur ein Drittel einer ganzen Kugel ausmacht). Meinen Anspruch nach Ästhetik erfüllt sie, nur ist sie als Elementarbaustein der Materie nicht brauchbar. Mit ihr kann der Raum nicht lückenlos besetzt ("parkettiert") werden (keine Überraschung, sonst wäre sie wohl in der Kristallographie bekannt).

8. Die kristallographischen Elementarzellen und ihre Packungsdichten   ↑ Anfang

Die in der Kristallographie gebrauchten Elementarzellen sind größer als die von mir in den Abschnitten 4.1 und 4.2 gebildeten "Stammzellen". Letztere genügten für die Berechnumng des Werts der dichtesten Kugelpackung. Form und Größe der kristallographischen Elementarzellen sind anders, damit sie der Aufgabe genügen, kleinste Bausteine für die lückenlose Zusammensetzung der Materie zu sein. Den Wert der dichtesten Kugelpackung kann man mit ihnen auch berechnen.

8.1  Die Packungsdichte der kubisch-flächenzentrierten Elementarzelle   ↑ Anfang

Die kubisch-flächenzentrierte Elementarzelle ist sogar etwas eleganter als meine zu ihr alternative Stammzelle, weil bei ihr alle Kugeln mittig geschnitten sind. Die Addition dieser Kugelteile zum Gesamtvolumen, das die Kugeln in der Zelle besetzen, ist mit Blick auf ein Zellen-Bild (Abb.18-links) lediglich Kopfrechnen: 8 Stück Achtel-Kugeln innerhalb der 8 Ecken plus 6 Stück Halb-Kugeln innerhalb der 6 Seiten haben das Volumen von 4 ganzen Kugeln (8·1/8 + 6·1/2 = 4).
In Abb.19-rechts ist meine Stammzelle in die Elementarzelle hineingezeichnet. Sie ist halb so hoch wie die Elementarzelle. Eine Kontrollrechnung ist nicht unbedingt erforderlich; ein Vergleich durch Messen in den maßstäblich gleichen Abbildungen kann genügen. Durch die diagonale Lage in der Elementarzelle ist ihre Grundfläche halb so groß wie die Letzterer. Somit ist ihr Volumen ein Viertel des Elementarzellenvolumens. Der kugelige Volumen-Anteil in der Stammzelle ist identisch mit dem einer ganzen Kugel. Die Stammzelle ist vier mal kleiner als die Elementarzelle und enthält nur eine anstatt vier Kugeln. Also haben beide Zellen die gleiche Packungsdichte.

Selbstverständlich kann der Wert der Packungsdichte in einer Elementarzelle auch separat berechnet werden. Die Vorkenntnis des Rechenergebnisses für die Stammzelle ist nicht erforderlich. Bei den Kristallographen sind meine Stammzellen ziemlich sicher unbekannt.

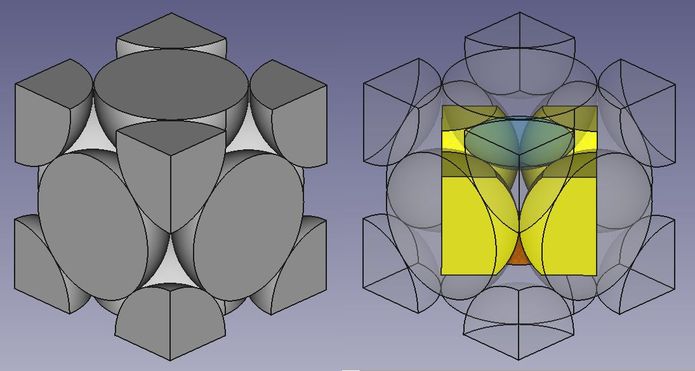Abb.19  Kubisch-flächenzentrierte Zellen: Elementarzelle (links) und Stammzelle in Elementarzelle (rechts)

8.2  Die Packungsdichte der hexagonalen Elementarzelle   ↑ Anfang

Die hexagonale Elementarzelle ist gegenüber der hexagonalen Stammzelle weniger im Vorteil, denn bei ihr werden Kugeln auch außermittig geschnitten (allerdings nur die inneren und nicht alle beteiligten wie bei der Stammzelle). Die Aufteilung der weggeschnittenen Kalotten ist weniger leicht überschaubar. Allenfalls ist eine geometrische Rechnung erforderlich. Ich unterlasse sie und vertraue darauf, dass aus dem Bild (Abb.20-links) eindeutig genug ersichtlich ist, dass die Kalotten (rechts) genau auf die Schnittflächen der Kugel (links) passen. Kopfrechnen in Verbindung mit einem Blick auf dieses Bild erbringen, dass die Elementarzelle vom Volumenwert zweier ganzer Kugeln besetzt ist: 8 Stück Achtel-Kugeln innerhalb der 8 Ecken + eine ganze Kugel ausmachende drei Kugelteile tiefer im Inneren (8·1/8 + 1 = 2).
Meine Stammzelle ist aus dem oberen und den unteren Viertel der Elementarzelle zusammengesetzt. Ihre Höhe ist die Hälfte der der Elementarzelle (Messen in den maßstäblich gleichen Abbildungen sollte erneut als Nachweis dafür genügen). Ich habe sie ungeteilt über das untere Viertel der Elementarzelle gezeichnet (Abb.19-rechts). Die Grundflächen beider Zellen sind gleich. Die Stammzelle ist halb so groß wie die Elementarzelle und enthält nur eine anstatt zwei Kugeln. Also haben beide Zellen die gleiche Packungsdichte.

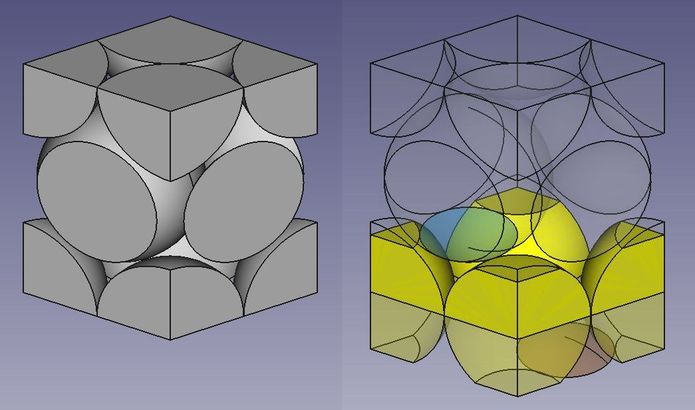Abb.20  Hexagonale Zellen: Elementarzelle (links) und Stammzelle (teilweise über Elementarzelle gezeichnet, rechts)

9. ABA und ABCA — in der Krisrallographie gebrauchte Kürzel beim Stapeln
     hexagonaler Kugelschichten   ↑ Anfang

Der kristalline Aufbau der Materie ist gut als Folge aufeinandergelegter hexagonal gemusterter Kugelschichten vorstellbar. Die Kristallisation schreitet aber nicht derart fort, dass erst eine Kugelschicht fertig gestellt wird, bevor die Kristallisation auch in der dritten Dimension stattfindet. Die Kristalle wachsen gleichzeitig in alle Richtungen. Das Stapeln von Schichten ist ein Gedankenexperiment, ebenso wie es der Gitteraufbau der Materie ist. Der Gitteraufbau erlaubt den Anschluß an die Beobachtung, dass kristalline Materie in der Lage ist, Röntgenstrahlen zu beugen. Über das Stapeln von Schichten findet man zu den dichtest möglichen Kugelpackungen, der hexagonalen und der kubisch-flächenzentrierte Elementarzelle. Die Elementarzelle ist wiederum nur ein ein ordnendes kristallographisches Gebilde, der kleinste natürliche Baustein ist das Atom.

Wie geht das Stapeln vor sich?

Die beiden verschiedenen Elementarzellen werden dadurch kenntlich, dass identisch getaltete Schichten nach dem gegenseitigen Einrasten unterschiedlich in Schicht-parallelen Richtungen untereinander verschoben sind. Zur Erklärung des Stapelns (Legens) und des zu Verschiebens habe ich das folgende Schema entworfen (Abbildungen 21 und 22):

Jede Kugel in der Schicht ist von 6 in einer Ebene angeordneten Lücken umgeben. Ein durch die Lücken gebildeter "Lochkreis" ist aber nur und genau von 3 Kugeln besetzbar. Eine aufgelegte Schicht, deren Kugeln zuächst zentrisch übereinander liegen, kann auf zweierlei Art verschoben werden. Nach dem Verschieben sind entweder die schwarz oder die weiß markierten Lücken besetzt. Dabei braucht man nicht 6 sondern nur 2 Verschieberichtungen (z.B. die mit schwarzen Pfeilen gekennzeichneten, s. Abb.21-unten) zu beachten. Beim Verschieben in die anderen (farbigen) Richtungen bleibt das Ergebnis aus Symmetriegründen gleich. Die zentrisch auf die Kugel (die mit den rundum zeigenden Pfeilen) gelegte Kugel zieht lediglich je zwei andere Kugeln aus ihrer Schicht (ihr und miteinander direkt benachbart) zum Lochkreis mit.

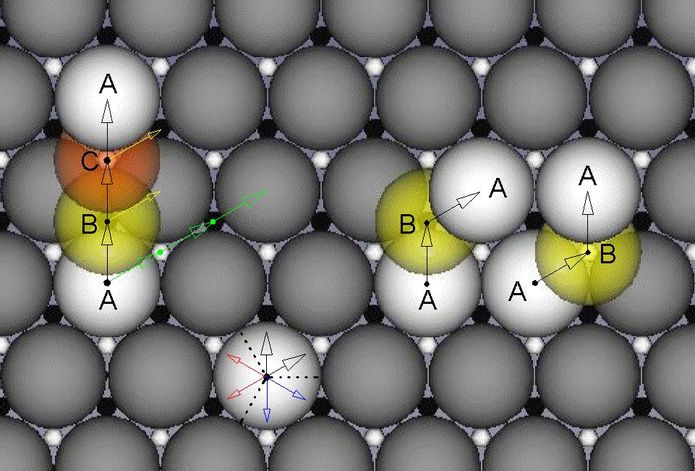Abb.21  Stapel-Reihenfolgen hexagonaler Kugel-Schichten
             unten: 6 mögliche Verschieberichtungen für eine deckungsgleich auf eine untere gelegte obere Schicht, von
                       denen nur 2 Richtungen (z.B. in Richtung der schwarzen Pfeile) praktische Bedeutung haben
             rechts: ABA-Folge (2 Varianten)
             links: ABCA-Folge (2. Variante mit grünen Pfeilen angedeutet;
                                         gelbe Pfeile führen zu einer kurzen Folge: ABA ab gelb, BCB ab rot)

9.1  Die ABA-Stapelfolge   ↑ Anfang

Rechts in Abb.21 ist die Stapelfolge ABA dargestellt. Sie entsteht auf zweierlei Weise. Im links gezeigten Fall wurde über eine weiße Kugel der unteren A-Schicht eine gelbe der darüber folgenden B-Schicht gelegt und dann nach oben (Richtung im Bild) bis zur Lücke verschoben. Auf die gelbe Kugel wurde eine weiße Kugel gelegt und dann nach halb-rechts verschoben. Alle Kugeln der Schicht, zu der sie gehören, liegen zentrisch (eingerastet in den Lücken direkt darunter) über den Kugeln der untersten Schicht, mit der das Stapeln begann. Deshalb wird diese Schicht auch als eine A-Schicht bezeichnet.
Im rechts gezeigten Fall wurde auf umgekehrten Weg (Verschiebung erst nach halb-rechts und danach nach oben) das gleiche Ergebnis erzielt.
Die ABA-Stapelung ist diejenige mit der kleinsten Stapelhöhe ohne Wiederholung: 2 Schichtabstände zwischen 3 Schichten. Sie führt zur hexagonalen Elementarzelle (s. Abb.17), dem ersten in der Kristallographie zur Beschreibung der Materie-Struktur in dichtester Packung konstruierten kleinsten Baustein.

9.2  Die ABCA-Stapelfolge   ↑ Anfang

Das Schema für die nächst-kleinste Stapelhöhe ohne Wiederholung ist ABCA und ist links in Abb.21 angewendet. Alle 3 aufgelegte Schichten wurden nach oben verschoben, bevor sich die zu oberst gelegene wieder zentrisch über der untersten einfand. Das gleiche Ergebnis kommt auch zustande, wenn man 3 mal nach halb-rechts verschiebt (angedeutet mit grünen Pfeilen).
Die ABCA-Schichtung enhält 3 Schichtabstände zwischen 4 Schichten und führt zur kubisch-flächenztentrierten Elementarzelle (s. Abb.15), dem zweiten in der Kristallographie zur Beschreibung der Materie-Struktur in dichtester Packung konstruierten kleinsten Baustein.

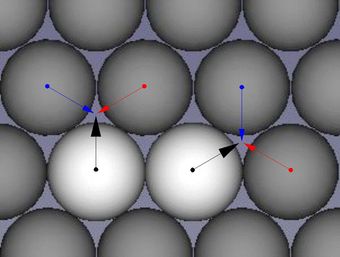<< Abb.22  Richtungen beim relativen Verschieben
                  einer aufgelegten Schicht

Zentrisch über der Ausgangsschicht liegt frühestens die zweit-nächste und spätestens die dritt-nächste Schicht. Eine längere Folge verschieden liegender Schichten ist nicht möglich, denn es gibt nur drei Liege-Möglichkeiten: die Ausgangslage und je eine Lage über einer schwarz und über einer weiß markierten Lücke.

Abb.22 enthält eine Ergänzung dazu, dass nur 2 der formal 6 Verschieberichtungen einer aufgelegten Schicht relevant sind. Die Verschiebung einer zentrisch auf die weiße Kugel gelegte Kugel in eine bestimmte Lücke ist identisch mit dem schrägen Zurückschieben einer von zwei nebenan aufgelegten Kugeln.

9.3 Quadratisch gemusterte Kugelschichten   ↑ Anfang

Die bei Kanonenkugelpyramiden bevorzugte quadratisch gemusterte Kugelschicht (Abb.3-links) hat keine allgemeine Bedeutung und spielt in der Kristallographie keine Rolle.

<< Abb.23  kubisch-flächenzentrierte Elementarzelle an
                  der Ecke eines Kugelwürfels (s.a. Abb.14)
                  flächenzentrierte Kugeln (gelb) sind markiert

Es erstaunt, dass das quadratische Muster des Gitterwürfels kubisch-flächenzentrierte Elementarzelle, die eine der beiden einzigen Bausteine der dichtest gepackten Materie ist, nicht in Verbindung mit einer quadratisch gemusterten Kugelschicht erwähnt wird. Das Erstaunen verschwindet, wenn man sich klar macht, dass Letztere lediglich ein anderer Blick hinein in hexagonal gemusterte Schichten ist, und dass diese zur umfassenden Beschreibung offensichtlich besser geeignet sind.

Ich habe zwar eine kleine quadratische "Stammzelle" gebildet (Abb.15), diese aber nur zur Berechnung des Wertes der dichtesten Kugelpackung benutzt. Da allerdings im quadratischen Muster einer Kugelschicht (Rastermass = 1, Kugeldurchmesser = 1·d) auch eine gegen diese um 45° verdrehte Seite einer kubisch-flächenzentrierten Elementarzelle (Kantenmaß = √2·d) sichtbar wird (dünne schwarze Linie in Abb.4-links), vermute ich, dass Letztere auch von dort aus leicht aufspürbar ist. In Abb. 23 sind sogar drei Seiten dieser Elementarzelle gut zu erkennen.

10. Kugelpyramiden-Varianten   ↑ Anfang

Die Kugelpyramiden, mit denen diese Arbeit beginnt (siehe Abbildungen 1 und 2), unterscheiden sich in der Neigung ihrer Wände (und davon abhängig auch in ihrer Höhe bei gleich vielen horizontalen Schichten). Das Muster auf den Wänden ist aber gleich und ein Indiz dafür, dass eine (besser im Inneren erkennbare) Grundeigenschaft gleich sein muss. Diese ist die ABCA-Folge hexagonal gemusterter Schichten und die damit verbundene Zusammensetzung aus kubisch-flächenzentrierten Elementarzellen.

10.1  Dreiseitige Kugelpyramiden   ↑ Anfang

Die Wände der in 5.1 durch Umlegen hexagonaler Schichten hinzugekommenene dreiseitige Pyramide (Abb.11-rechts, Überhängendes gekappt) ist (ebenso wie die vierseitige Pyramide, siehe unten) weniger steil (35,26° fehlen an senkrecht) als die dreiseitige Pyramide (nur 19,47° fehlen an senkrecht), aus der sie entstand. Dieser Unterschied ist auch in der Abb.21 erkennbar, und die angegebenen Winkel sind mit Hilfe dieser Abbildung berechenbar.
Das Wandmuster aus Abb.11-rechts (Kugeln in Falllinie übereinander) wird in Abb.21-links (Stapelfolge ABCA) wiederholt. Auf dem Weg in den Kugelstapel hinein wird eine unterste Kugelreihe übersprungen. Wählt man den mit grünen Pfeilen angedeuteten Weg, so ist die Stapelfolge ABCA bereits mit einer Kugel über der nächsten untersten Kugelreihe beendet, und die Wand fällt wesentlich steiler aus. Dem schrägen grünen Weg entspechen die auf den Wänden in Abb.2-rechts seitlich schräg ansteigenden Kugelreihen.
Die oben angegebenen Winkelwerte ergeben sich mit folgenden Größen (Langeneinheit = Kugekdurchmesser):
horizontaler Abstand zwischen den Kugelreihen in einer Schicht : h = √3/2 = 0,866,
vertikaler Abstand zwischen den Kugelschichten; v = √2/√3 = 0,8165 (entspricht h in Abb.10)
tan α₁ = 2·h / (3·v) >>> α₁ = 35,26°,
tan α₂ = 1·h / (3·v) >>> α₁ = 19,47°.

10.2  Die vierseitige Kugelpyramide   ↑ Anfang

Die vierseitige Pyramide (Abb.2-links) ist genau gleich wenig steil wie die dreiseitige aus Abb.11-rechts. Aus Abb.21 ist hiefür nichts erkennbar, und die Wandneigung ist mit ihrer Hilfe nicht berechenbar. Hier liegen hexagonal, dort aber quadratisch gemusterte Kugelschichtern übereinander.
Der Winkelwert kann aber ebenfalls leicht bestimmt werden:
Eine nächst am Schichtrand aufgelegte Kugel liegt um einen halben Kugeldurchmesser vom Rand entfernt und um √2/2 eines Kugeldurchmesser höher als die Kugeln darunter.
tan α₃ = ½ / (√2/2) >>> α₁ = 35,26°,
Auf diese Rechnung hätte auch verzichtet werden können, denn zwischen dem Objekt von Abb.11-rechts und dem Objekt in Abb.12 wurden nur die "Seiten gewechselt": was vorher Wand war, wurde zur Bodenfläche und umgekehrt. Der Winkel zwischen beiden Flächen wurde als α₁ bereits berechnet.

10.3  Eine sechseitige Kugelpyramide   ↑ Anfang

Im Abschnitt 3. habe ich über Vielfache des regelmäßigen Dreiecks (z.B. Raute und Sechseck) spekuliert. Von den dazu erstellten virtuellen Modellen habe ich in Abb.24 die regelmäßige sechsseitige Pyramide aufgenommen, hier als Zwischenform zwischen zwei dreiseitigen Pyramiden.
   Links befindet sich die dreiseitige Pyramide von Abb.11-rechts (Überhängendes entfernt),
   in der Mitte die durch Kappen der Ecken dieser Pyramide entstandene regelmäßige sechsseitige Pyramide und
   rechts die durch Wegnehmen weiterer Kugeln entstandene dreiseitige Pyramide wie in Abb.2-rechts und Abb.11-links
      (nur etwas weniger hoch).
      Weiteres Wegnehmen von Kugeln, um wieder zur dreiseitigen Pyramide zu kommen, ist nicht möglich. Der Turm würde einstürzen.
Die sechsseitige Pyramide ist ein "Zwitter". Auf drei Seiten ist sie hexagonal, und auf den drei dazwischen befindlichen Seiten ist sie quadratisch gemustert.

Abb.24  Kugel-Pyramiden:  dreiseitig >> sechsseitig >> dreiseitig
             oben: Ansichten von vorn
             unten: Draufsichten

10.4  Eine aus hexagonalen Elementarzellen bestehende Kugelpyramide   ↑ Anfang

Als Letztes war die Frage zu klären, warum alle bekannten (Kanonen-)Kugelpyramiden ausschließlich aus kubisch-flächenzentrierten Elementarzellen zusammengesetzt sind. Ein aus hexagonalen Elementarzellen erstelltes mögliches Modell ist in Abb.25 gezeigt. Darin sind die erkennbar: Die Wände sind nicht glatt sondern gestuft. Es ist ein Ding zwischen den beiden äußeren Pyramiden von Abb.24. Auf gleicher Grundfläche kann man weniger Kugeln stapeln als bei der Standard-Pyramide, rechts. Man kann relativ mehr Kugeln stapeln als bei der quadratisch gemusterten, links. Beide werden offensichtlich als raumverschwenderisch angesehen, auch und insbesondere die linke, die ebenfalls nicht vorkommt.

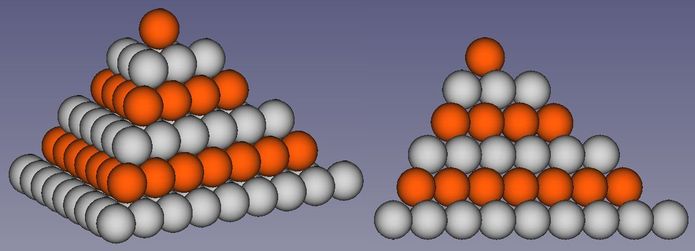Abb.25  Eine aus hexagonalen Elementarzellen bestehende Kugelpyramide: "Stufenpyramide"
            (ABA-Folge hexagonaler Schichten)

11. Literatur   ↑ Anfang

[1]   Dostert, Krupp, Rolfes: Das Problem der Kugelpackung
       Schnappschüsse moderner Mathematik aus Oberwolfach, N^o4, 2016.
[2]   Siegfried Wetzel: Kreis- und Kugel-Förmiges
[3]   Karl Gerstner: Das Apollonische in der Kunst — Max Bill zum 80.
                       in: Die Liebe zur Geometrie. Acht Porträts. du, Oktober 1988
[4]   Universität Freiburg: Vorlesungen über Anorganische Chemie, Abb. 3.2.1. Strukturen der metallischen Elemente
[5]   Michael Schmidt: Chemie verstehen
       Die Elementarzellen und... — Die Elementarzelle — Die Elementarzelle der hexagonal dichtesten Kugelpackung — drittes Bild, links

Siegfried Wetzel, CH 3400 Burgdorf, April 2020

 ↑↑ Anfang

<< Home
<< anderes Geometrisches