<< Home
<< andere Farbe-Beiträge
↓↓ Ende
Geometrische Optik, optische Abbildung und
Scheimpflug-Regel
Inhalt
1. Geometrische Optik2. Optische Abbildung
2.1 Sonderfall: Gegenstands- und Bildebene sind untereinander parallel
2.2 Allgemeiner Fall: Gegenstands- und Bildebene sind gegeneinander geneigt
3. Scheimpflug-Regel
3.1 Kontrolle mit geometrischer Konstruktion
3.2 Kontrolle mit geometrischer Ähnlichkeit von Dreiecken
3.3 Kontrolle mit Geradengleichungen
4. Literatur
1. Geometrische Optik ↑ Inhalt
Die geometrische Optik oder Strahlenoptik hat einfache Gesetze, mit der ein großer Teil der Aufgaben in der technischen Optik gelöst werden kann, entwickelt [1]. Eines der Grundgesetze behandelt die geradlinige Ausbreitung des Lichtes in Form von linienförmig gedachten Lichtsstrahlen. Ausgehend von punktförmig gedachten Lichtquellen breiten sie sich in alle Richtungen aus und stören sich gegenseitig nicht. An der Grenze zu einem undurchsichtigen Medium können sie so reflektiert (gespiegelt) werden, dass ihre Linienform erhalten bleibt. An der Grenze zu einem anderen durchsichtigen Medium können sie als kompakte Linien ebenfalls erhalten bleiben. Dort werden sie lediglich scharf abgelenkt (gebrochen).
2. Optische Abbildung ↑ Inhalt
Eine der Hauptaufgaben der Optik besteht darin, von einem Gegenstand (Ding, Objekt) ein Bild zu erzeugen. Dafür wird meistens eine Linse (oder als Objektiv bezeichnete Linsenkombinationen) verwendet, und für die strahlenoptische Beschreibung der dabei stattfindenden Vorgänge werden die Linsengleichung und eine zugehörende geometrische Konstruktion angewendet. Auf zeichnerischem Wege wird der von einer Linse erzeugte Bildpunkt eines Gegenstandpunktes gefunden. Die Linsengleichung beschreibt den Zusammenhang zwischen den Abständen (Gegenstandsweite und Bildweite) der beiden Punkte in Abhängigkeit von der Brennweite der Linse. Die Linse wird oft näherungsweise als flache Linse angesehen, was heist, dass die beiden Brechungen zu einem einzigen Abknicken in der Mittelebene der Linse zusammengefasst werden. Die Konstruktion vereinfacht sich, indem mit Strahlen, die ungebrochen durch den Mittelpunkt der Linse (Mittenstrahl) bzw. durch ihren Brennpunkt (achsparalleler Strahl, gebrochen zu Brennstrahl) verlaufen, gearbeitet werden kann. Das Bild des geamten Gegenstandes besteht schließlich aus Bildpunkten mehrerer Dingpunkte.
2.1 Sonderfall: Gegenstands- und Bildebene sind untereinander parallel ↑ Inhalt
Die geometrische Konstruktion der optischen Abbildung wird in der Literatur meistens mit einer Zeichnung wie der in Abb.1 gezeigten beschrieben. Dabei handelt es sich aber um einen Sonderfall, bei dem die Konstruktion eines einzigen Bildpunktes aus einem einzigen Gegenstanpunkt (Spitze eines Pfeils als Gegenstand- bzw. Bildpunkt) genügt. Alle anderen Bildpunkte befinden sich in derselben, zur Linsenebene ebenfalls parallelen Bildebene. Der Abbildungsmaßsstab b/g ist für alle Punkte-Paare dergleiche. Bild und Gegenstand sind maßstäblich gleich. Mit dieser Kenntnis lässt sich das Bild auf einfache Weise komplettieren.
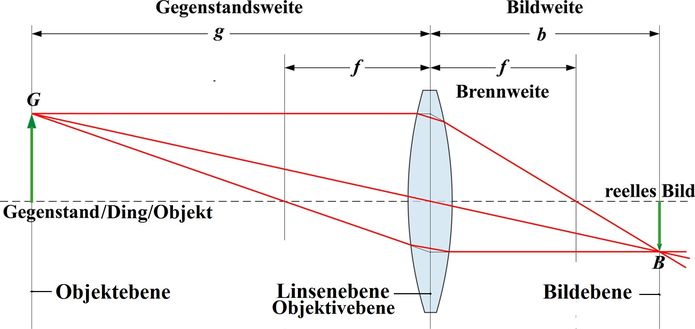 Abb.1: Gegenstands- und Bildebene sind untereinander parallel (Wikipedia)
Abb.1: Gegenstands- und Bildebene sind untereinander parallel (Wikipedia)
2.2 Allgemeiner Fall: Gegenstands- und Bildebene sind gegeneinander geneigt ↑ Inhalt
Im allg. Fall befindet ist ein abzubildender ebener Gegenstand nicht in einer zur Linsenebene senkrechten, sondern in einer dieser gegenüber geneigten Ebene (Abb.2). Das Bild liegt dann auch in einer gegenüber der Linsenebene geneigten Ebene. Wenn die Ebene, in der das Bild aufgefangen wird (auf Mattscheibe, Film oder Bildsensor), scharf sein soll, so ist die Auffangebene in diese geneigte Bildebene zu bringen. Diese Bedingung nennt man Scheimpflug-Bedingung (nach dem KartografenTheodor Scheimpflug, der sie um 1900 erstmals intensiv befolgte). Zu befolgen ist die Regel (Scheimpflug-Regel), dass optimale Abbildungsschärfe besteht, wenn die drei Ebenen (Gegenstands- Linsen- und Bildebene) so relativ zueinander positioniert sind, dass sie sich in einer Geraden schneiden.
3. Scheimpflug-Regel ↑ Inhalt
Die Scheimpflug-Regel ist kein besonderes Gesetz der Strahlenoptik oder seiner Anwendung für die optische Abbildung. Sie ist lediglich eine besondere Aussage, die in der allgemein gültigen Linsengleichung bereits angelegt ist. Sie herauszustellen, wird im Folgenden versucht.
Zur Konstruktion wird eine Schnittzeichnung verwendet. Sie enthält die Linsenachse und stellt die zu ihr senkrechte Linsenebene als Schnittgerade dar. Sie wird zusätzlich so gelegt, dass auch die Gegenstands- und die Bildebene senkrecht zum Zeichenblatt liegen und dieses durch ihre jeweilige Schnittgerade mit dem Zeicheblatt repräsentiert werden. Diese Geraden werden schließlich mit je zwei Punkten vollständig beschrieben. Man beachte, dass im Folgenden immer von der Gegenstands- und der Bildebene (und der Linsenebene) gesprochen wird, obwohl sie in den dabei benutzten Zeichnungen lediglich als Schnittgeraden mit der Zeichenebene erscheinen.
Die Aufgabe zur Bestätigung der Scheimpflug-Regel ist, das ebene Bild der Gegenstandsebene zu finden und zu zeigen, dass beide Ebenen sich mit der Linsenebene in derselben Geraden schneiden.
Die Gegenstandsebene wird mit den zwei Punkten G auf ihrer Schnittgeraden vorgegeben (Abb.2). Die Bildebene wird mit den zwei Bildpunkten B gefunden.
Zur Vereinfachung der später folgenden Auswertung wird G1 in die Linsen-Achse gelegt, und in einer Nebenkonstruktion (Punkte G'1 und B'1) wird der auch darin liegende Bildpunkt B1 ermittelt. Der zweite Objektpunkt G2 bekommt eine allgemeine Lage. Er befinde sich seitlich der Achse und näher an der Linsenebene. Weil auf dieser Seite der Achse der Schnitt zwischen Gegenstands- und Linsenebene erfolgen wird, ist auf dem Zeichenblatt zunächst freier Platz gelassen). Die Konstruktion seines Bildpunktes B2 ist die gegenüber dem Sonderfall (Abb.1) zusätzliche Maßnahme.
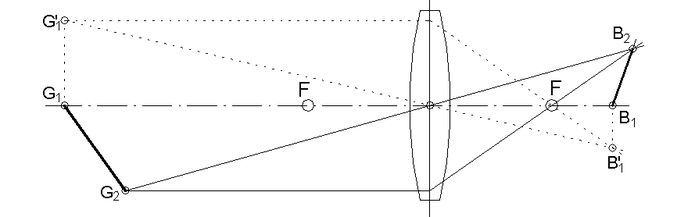 Abb.2: Konstruktion der Bildpunkte von zwei vorgegebenen Gegenstandspunkten
Abb.2: Konstruktion der Bildpunkte von zwei vorgegebenen Gegenstandspunkten
Aus der Vertrautheit mit älteren Fotoapparaten, an denen das Eintsellen der Entfernung noch manuell erfolgte, ist bekannt, dass man für einen näheren Gegenstand das Objektiv weiter von der Filmebene zu entfernen hat (die Objektivlinse wurde "heraus geschraubt"). Im einfachen Mattscheibensucher bemerkte man das Vertauschen zwischen rechts und links. Somit hat man das Bild des zweiten Gegenstandspunktes auf der anderen Seite der optischen Achse und etwas weiter entfernt als jenes des ersten Gegenstandspunktes zu erwarten. Verbindet man bereits in Gedanken die je zwei Gegenstands- bzw. Bildpunkte miteinander, so erkennt man, dass sich beide gefundenen Geraden auf derselben Seite mit der Schnittgeraden der Linsenebenene schneiden werden. Der Nachweis dafür, dass sie das in einem gemeinsamen Punkt tun werden, hat quantitativ durch zeichnerische Konstruktion und/oder geometrisches Rechnen zu erfolgen.
3.1 Kontrolle mit geometrischer Konstruktion ↑ Inhalt
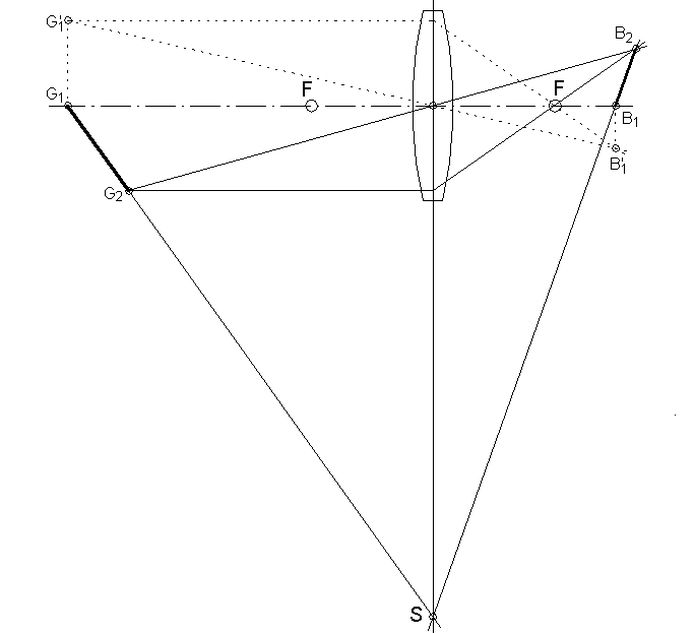 Abb.3: Die Geraden/Ebenen, die die beiden vorgegebenen Gegenstandspunkte bzw. konstruierten Bildpunkte enthalten schneiden sich mit der Linsengeraden/-ebene im gleichen Punkt S.
Abb.3: Die Geraden/Ebenen, die die beiden vorgegebenen Gegenstandspunkte bzw. konstruierten Bildpunkte enthalten schneiden sich mit der Linsengeraden/-ebene im gleichen Punkt S.
Der Nachweis mittels zeichnerischer Konstruktion ist gemäß Abb.3 offensichtlich mit guter Genauigkeit gelungen.
3.2 Kontrolle mit geometrischer Ähnlichkeit von Dreiecken ↑ Inhalt
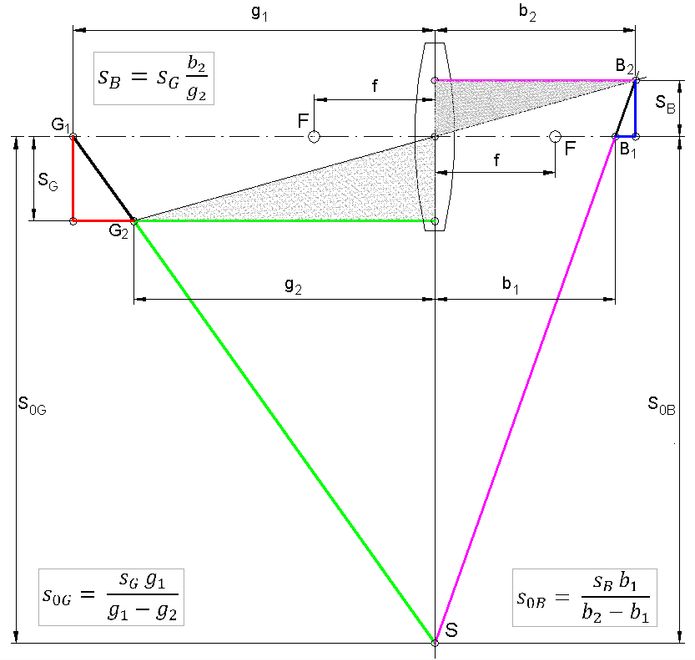 Abb.4: Die Zeichnung ist für Ähnlichkeits-Betrachtungen vorbereitet.
Abb.4: Die Zeichnung ist für Ähnlichkeits-Betrachtungen vorbereitet.
In Abb.4 sind die Längen eingetragen, die für die Kontrolle der Scheimpflug-Regel über Ähnlichkeit von Dreiecken gebraucht werden.
Bestimmt wird die Länge s0 (Abstand des Scheimpflug-Punktes S von der Linsenachse) einmal mit den die Lage der Gegenstandspunkte kennzeichnennden Längen, ein zweites mal mit denen der Bildpunkte. Die Längen der Bildpunkte werden dann mit den Längen der Gegenstandspunkte ausgedrückt, wobei die in der Linsengleichung enthaltenen Zusammenhänge gebraucht werden. Das Ergebnis für s0 muss beide Male gleich sein.
Auf der Gegenstandsseite ähneln sich das rot gezeichnete und das grün gezeichnete Dreieck. Auf der Bildseite sind das blau und das magenta gezeichnete Dreieck einander ähnlich. Aus den beiden Ähnlichkeiten ergeben sich die beiden in Abb.4 unten eingetragenene Beziehungen für s0 (zunächst getrennt als s0G und s0B bezeichnet).
Die Linsengleichung ist: 1/g + 1/b = 1/f. Nach der Bildweite aufgelöst lautet sie : b = f·g / (g-f).
Somit können in der rechts stehenden Beziehung (s0B) die Bildweiten b1 und b2 durch die Gegenstandsweiten g1 bzw. g2 (und die Brennweite f) ersetzt werden.
Für den Ersatz von sB wird die gegenseitige Ähnlichkeit der beiden grau gefüllten Dreiecke ausgenutzt. Für sB ergibt sich die links oben in Abb.4 eingetragene Beziehung, in der noch b2 wie eben gesagt zu ersetzen ist.
Die Beziehung für s0B ist nach dem Austausch ihres Inhalts ziemlich unübersichtlich geworden. War sie doch schon ein Bruch mit einer Differenz im Nenner, so wurden alle vier ihrer Teile wieder durch Brüche mit je einer Differrenz im Nenner ersetzt. Aber, was zu erwarten war (was zum Ruhme Schleimpflugs sein musste), es ließ sich vieles kürzen, und das Resultat ist: s0B = s0G = s0, q.e.d.
Erstaunlich erscheint zunächst, dass die Brennweite auch entfallen ist, dass der Scheimpflugpunkt bei allen Linsen oder Objektiven sich an derselben Stelle befindet. Es bedarf aber wenig Nachdenken, um die Richtigkeit dieses Ergebnisses zu erkennen. Die geneigte Gegenstandsebene bestimmt diesen Punkt bzw. diese Gerade, und von ihr ist allein derjenige Winkel bedeutsam, den sie mit der Linsenebene bildet. Nur die Lage der Bildebene ist zusätzlich von der Linsenebene abhängig. Zu jeder/m Linse/Objektiv mit anderer Brennweite gehört eine andere Bildebene, die aber alle die von der Gegenstands- und Linsenebene gebildete Schnittgerade enthalten.
3.3 Kontrolle mit Geradengleichungen ↑ Inhalt
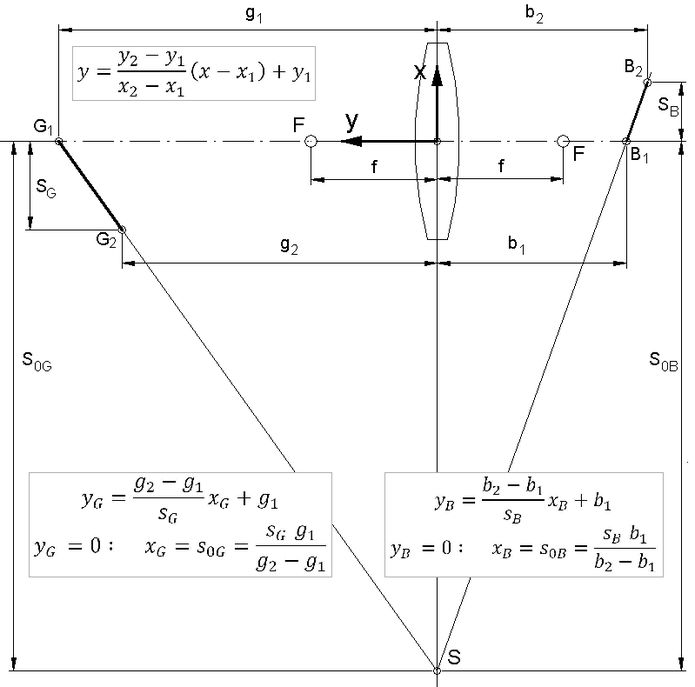 Abb.5: Der Zeichnung ist ein x-y-Koordinatensystem überlagert.
Abb.5: Der Zeichnung ist ein x-y-Koordinatensystem überlagert.
In Abb.5 ist der Zeichnung ein x-y-Koordinatensystem überlagert, das zum Aufstellen von Geradengleichungen für die Schnittgeraden der Gegenstands- und der Bildebene mit dem Zeichenblatt benutzt wird.
Mit den je zwei Gegenstands- und Bildpunkten lassen sich zwei Gleichungen für Geraden (in Zweipunkteform) aufstellen. Der Schnittpunkt der Geraden mit der Linsenebene (im Bild: mit der "Linsengeraden") ist jeweils ihr Nullpunkt (x-Wert bei y=0). Der Nachweis für die Scheimpflug-Regel ist erbracht, wenn die beiden Nullpunkte identisch sind.
Der allgemeine Ausdruck für die Zweipunkteform der Geradengleichung ist oben links in der Abb.5 eingetragen.
Mit den x- und y-Kordinaten der Punkte G und B sind die zuerst unten in Abb.5 eingetragenen besonderen Formen dieser Gleichung entstanden (Abkürzungen ergaben sich mit x1=0 und mit sG bzw. sB für x2-x1=0)
In der Zeile darunter steht jeweils am Schluss der Ausdruck für den Nullpunkt der jeweiligen Gerade.
Jeder der beiden Nullpunkt-Ausdrücke ist identisch mit dem jeweils unten in Abb.4 stehenden Ausdruck.
Man stolpere nicht über Vorzeichenunterschiede. Diese verschwinden, wenn man beachtet, dass zu einem Koordinatenwert grundsätzlich immer ein Vorzeichen gehört, und wenn man dieses berücksichtigt.
Die Rechenarbeit, die Beziehung für s0B mit den Koordinaten der Gegenstandspunkte auszudrücken, braucht nicht wiederholt zu werden.Das Resultat steht fest. Es ist dasgleiche wie im Abschnitt 3.2: s0B = s0G = s0, q.e.d.
Abschnitt 3.3 hätte eigentlich entfallen können, denn es wurden die prinzipiell gleichen Grundsätze wie im Abschnitt 3.2 angewendet. Die dem Problem innewohnenden Beziehungen lassen sich sowohl geometrisch (ähnliche Dreiecke, Strahlensätze in 3.2) als auch algebraisch (Geradengleichungen in 3.3) darstellen und behandeln.
4. Literatur ↑ Inhalt
[1] Alfred Recknagel: Experimentalphysik, Teil Elektrik und Optik, P.E. Blank - Verlag, Weimar, 1953, S. 242
![]() Siegfried Wetzel, CH 3400 Burgdorf, Februar 2018
Siegfried Wetzel, CH 3400 Burgdorf, Februar 2018
↑↑ Inhalt
<< Home
<< andere Farbe-Beiträge