|
<< Home Der ModulorInhalt1. Einleitung2. Geometrische Folgen 3. Anwendung der Renard-Serien 4. Anwendung des Modulor 5. Was bleibt vom Modulor? 6. Wie ist der Modulor entstanden? 7. Literatur 1. Einleitung
Der Architekt Le Corbusier stellte zwei Reihen von Längen-Normalen auf, die er zur Verwendung nicht nur in der Architektur, sondern in der gesamten Technik empfahl. Er veröffentlichte diese unter dem Titel Der Modulor, ein in Architektur und Technik allgemein anwendbares harmonisches Maß im menschlichen Maßstab [1].
Le Corbusier betont, dass seine Reihen Fibonacci-Folgen seien. Damit hat er aber nichts Besonderes geschaffen, denn der Quotient zwischen zwei aufeinander folgenden Fibonacci-Zahlen ist von "mathematischer Natur" aus eine Näherung an den Quotienten des Goldenen Schnitts. Diese Näherung ist umso besser, je größer die darin enthaltenen Zahlen sind (im Modulor werden relativ große Zahlen verwendet). Formal hat Le Corbusier Unrecht, denn als Fibonacci-Folgen werden nur Folgen ganzer Zahlen (natürliche Zahlen) bezeichnet. 2. Geometrische FolgenDie Reihen des Modulor sind geometrische Folgen, deren Eigenschaft der konstante Quotient zweier benachbarter Folgenglieder ist. Beim Modulor ist es der Quotient des Goldenen Schnitts.In der Technik sind die sogenannten Renard-Serien gebräuchlich. Die in ihnen enthaltenen Werte werden im Allgemeinen als Nomzahlen bezeichnet und sind Gegenstand der Normen DIN 323 und ISO 3. Die Serie R5 (weitere Serien: R10, R20 und R40) hat den Quotient 1,585 (fünfte Wurzel aus zehn) und ist somit den Modulor-Reihen sehr ähnlich. Benutzt man dort ebenfalls 113 bzw. 226 als Bezugswerte, so entstehen die beiden, der Roten bzw. Blauen Modular-Reihe vergleichbaren Serien: entsprechend Roter Reihe: ... 17,9 28,4 45,0 71,3 113 179 284 450 713 ... entsprechend Blauer Reihe: ... 22,6 35,8 56,8 90,0 143 226 358 568 ... Eine beide Reihen enthaltende Renard-Serie ist die Serie R10 mit dem Quotienten 1,259 (zehnte Wurzel aus zehn): ... 17,9 22,6 28,4 35,7 45,0 56,6 71,3 89,8 113 142 179 225 284 357 450 566 713 ... 3. Anwendung der Renard-Serien
Die Werte der in der Technik gängigen Renard-Serien werden rein seriell angewendet: Es entstehen nebeneinander stehende ähnliche, in i.d.R. einer Abmessung abgestufte Objekte. Bei Le Corbusier handelt es sich nicht um in ihren Abmessungen abgestufte Zusammenstellungen mehrerer/vieler Objekte. Er benutzte vorwiegend die Modulor-Werte in beliebigen Zusammenstellungen (Additionen) an einem einzigen Objekt. Mit Renard-Serien werden Folgen aus ähnlichen Teilen (z.B. Schrauben) und Formen (z.B. Hohlformen wie Bohrungen) erstellt. Die dabei verwendete geometrische Abstufung ist insofern sinnvoll bzw. erforderlich, weil benachbarte größere Teile bzw. Formen in gleichem Verhältnis wie benachbarte kleinere Teile zueinander stehen "müssen". Das Muß ergibt sich aus dem Gebrauch. Bei linearer Abstufung würden die größeren Teile bzw. Formen einander immer gleicher. Sie besäßen keinen unterschiedlichen Gebrauchs-Nutzen mehr. 4. Anwendung des ModulorDie Situation für die Anwendung der Modulor-Reihen ist in der Architektur (wofür der Modulor primär gedacht war) deutlich anders als für die Renard-Serien in der Technik. Es gibt zumindest keine von Architekten zu entwerfende Bauwerk-Serien, wobei sich die einzelnen Bauwerke lediglich in ihrer Größe unterscheiden. In geometrischen Reihen angebrachte Teile oder Formen wären in den Bauwerken vermutlich auch eher eine Ausnahme. Le Corbusier legte die Modulor-Werte wohl als Glieder zweier geometrischen Folgen fest, betont aber, dass die Werte aus beiden Reihen in beliebiger Zusammenstellung (Addition) angewendet werden können (eine Parallele dazu ist die Zusammenstellung von Wägestücken bei einer Balkenwaage). Wenn allerdings eine Form mit enthaltenem Goldenen Schnitt zu verwirklichen ist, so kann nicht beliebig kombiniert werden, es muß je ein Wert aus beiden Reihen benutzt werden. Die Verwendung des Goldenen Schnitts als Proportionsverhältnis ist nicht überraschend, denn dieser gilt seit der Renaisance als ein hohes ästhetisches Ideal. Le Corbusier wollte es wiederbeleben mit der kontraproduktiven Zusatzbedingung, dass bei den absoluten Längenwerten ausschließlich am menschlichen Körper vorkommende benutzt werden. Der Erfolg seiner Bemühungen blieb aus. 5. Was bleibt vom Modulor?
Die Annahme, dass der Goldene Schnitt eine besondere ästhetische Bedeutung habe, hat sich als unberechtigt erwiesen. Sie war reine Ideologie. Diese Zahl hat zwar mathematisch faszinierende Eigenschaften – sie ist sozusagen mathematisch hochästhetisch. Es gibt aber keinerlei Beleg, dass unser Auge beim Anblick golden geschnittener Rechtecke besonders entzückt wäre oder sie besser findet als andere.
Le Corbusier hat gleich wie Renard die unendlich große Menge von Zahlen auf eine begrentzte Menge von Normzahlen reduziert. Renards Normzahlen wiederholen sich in praktisch vorteilhafter Weise im nächst-größeren Dezimalbereich mit zehn mal größeren Werten. Den Modulor-Zahlen fehlt diese vorteihafte Besonderheit, weil einerseits eine dafür unpassende willkürliche (Körpergröße 183 cm) Zahl dazugehören muss, und weil der Goldene Schnitt als Quotient der geometrischen Folgen dafür ungeeignet ist. 6.Wie ist der Modulor entstanden?Le Corbusier war ein verehrter und weltberühmter Architekt. Die Art und Weise, wie er den Modulor erarbeitete und darstellte, steht diesem Nimbus diametral entgegen. Der mathematisch-geometrische Aspekt dieses von ihm selbst als Erfindung bezeichneten Zusammenhangs machte ihm erhebliche Mühe, was zumindest heutige Leser ziemlich merkwürdig finden. Le Cobusier bekennt einerseits, dass ihm das Rechnen schon in der Schule Angst machte und Abscheu einflößte, dass er darin "ein Stümper war" [1, S.131]. Andererseits verfasst er im Modulor [1] ein ganzes Kapitel "Mathematik" (Kap.3). Erwarten könnte man, dass er darin seine nachgeholten Kenntnisse in einfacher Mathematik schildert. Das passiert aber nicht. Im Gegenteil, er wiederholt gleich im ersten Absatz seine Hilflosigkeit, wenn nicht sogar Angst gegenüber der Mathematik mit der Feststellung, dass diese "ein fremder Ort" sei, "wo die Götter wohnen" [1, S.73]. Danach spricht er bald wieder ganz allgemein von seiner unaufhörlichen und "uneigennützigen Leidenschaft und Pflicht" für die "Bemühung um Verhältnis und Maße" [1, S.82], aber nicht über die einfache Beziehung des Modulor zur Mathematik. Le corbusier verließ die Grundschule im Alter von 13 Jahren. Danach erlernte er an einer Kunstgewerbeschule die Handwerke Graveur und Ziselier. Der dortige Zeichenlehrer erweckte sein Interesse für Kunst und Architektur. So wurde er Maler, Bildhauer und Architekt, wobei er insbesondere für letzteres "den offiziellen Unterricht geflohen hatte" [1, S.29]. Mit 23 Jahren wollte er ein Haus bauen. Vor der bereits gezeichneten Fassade sitzend stellte sich ihm die "beängstigende Frage: Was ist das für eine Regel, die alles ordnet, alles verbindet?" Eines Tages "überkam ihn die Gewißheit einer Wahrheit: der rechte Winkel waltet über die Komposition: ... die Orte des rechten Winkels beherrschen" sie. "Dies wird ihm zu einer Offenbarung" [1, S.26]. Aus der Literatur erfährt er von regulierenden Liniennetzten, "um Kompositionen überlegt zu gestalten" 1, S.27]. In der Malerei erprobt er den Goldenen Schnitt, der neben dem Ort des rechten Winkels zum zweitenen Stichwort auf dem Jahrzehnte langen Weg zum Modulor werden wird. Der Modulor ist "eine Erleuchtung durch die unendlichen Ordnungen", die Le Corbusier haben konnte, "weil er nie vom Akademismus geplagt wurde" [2, S.131]. Als Leser aller dieser Zitate liegt der Eindruck nahe, dass er auch nie geplagt wurde, sich allgemein verständlich ausdrücken zu lernen. Einige seiner späteren Angestellten halfen ihm dabei, den Modulor nicht nur zu entwickeln, sondern über ihn auch zu sprechen (sie waren dabei aber nicht sicher, dass daraus einmal "mehr als ein ästhetisches Rezept" [2, S.41] werden wird). Die Gedanken von Le Corbusier dazu mussten sie immer mehr oder weniger erraten. Dem Leser seiner beiden Bücher [1] und [2] geht es ebenso. Im Folgenden wird dennoch versucht, das Erarbeiten des Modulor an Hand dieser Bücher in etwa darzustellen.
Der Anfang war die Suche nach einer "Regel, die alles ordnet" [1, S.26]. Dem folgte die "Offenbarung: der rechte Winkel waltet über die Komposition" [1, S.26]. Als zweites zu benutzendes "mathematisches Hilfsmittel" ergab sich aus Le Cobusiers Malerei der Goldene Schnitt [1, S.27]. Durch Beobachtungen, insbesondere auf Reisen durch mehrere Länder erkannte er die häufig angewandte Deckenhöhe von 2,10 bis 2,20 Meter. Er erwärmte sich für dieses Maß als die Höhe eines Mannes mit erhobenem Arm. Als er diese Deckenhöhe in seinen frühen Bauten verwendete, geriet er bereits in den Widerspruch zu Bauvorschriften. Le Corbusier hatte sich schon früh für Standardisierung bzw. für den Serienbau von Wohnhäusern (Wohnhaus "als Wohnmaschine"; [1, S.28] ausgesprochen. Endlich nach etwa 20 Jahren ging es weiter mit seinem Modulor. Er versuchte ihn genauer darzustellen, nämlich als Gegenentwurf zu Bau-Normen, die während des zweiten Weltkrieges in Frankreich erarbeitet worden waren. Er sprach jetzt vom "Gitter der Verhältnisse" ([1, S.37], der Name Modulor wurde später gefunden). Er verstand darunter eine geometrische Darstellung, die mit Geometrie in der Mathematik nichts zu tun hat. Sie spielt die Rolle eines für seine Gewohnheit der visuellen Welt-Betrachtung unverzichtbares Bild. Le Corbusier war übrigens seinem Gitter der Verhältnisse nie ganz sicher. Nachträglich machten ihn mehrere Mathematiker darauf aufmerksam, dass die Konstruktion mithilfe des ihm offenbarten "Ort des rechten Winkels" mathematisch nicht korrekt ist: Die beiden gefundenen Quadrate sind 1,006-fach zu groß. Praktisch ist das allerdings unbedeutend. Nur, die Maus zum Elefanten gemacht zu haben, könnte man ihm ankreiden. 7. Literatur[1] Le Corbusier: Der Modulor - Darstellung eines in Achitektur und Technik allgemein anwendbaren harmonischenMaszes im menschlichen Maszstab, 1953, J.G. Cotta'sche Buchhandlung Nachfolger, Stuttgart, Original 1948 in Französisch [2] Le Corbusier: Modulor 2 - 1955 - Fortsetzung von "Der Modulor" 1948, 1958, Deutsche Verlags-Anstalt, München
|
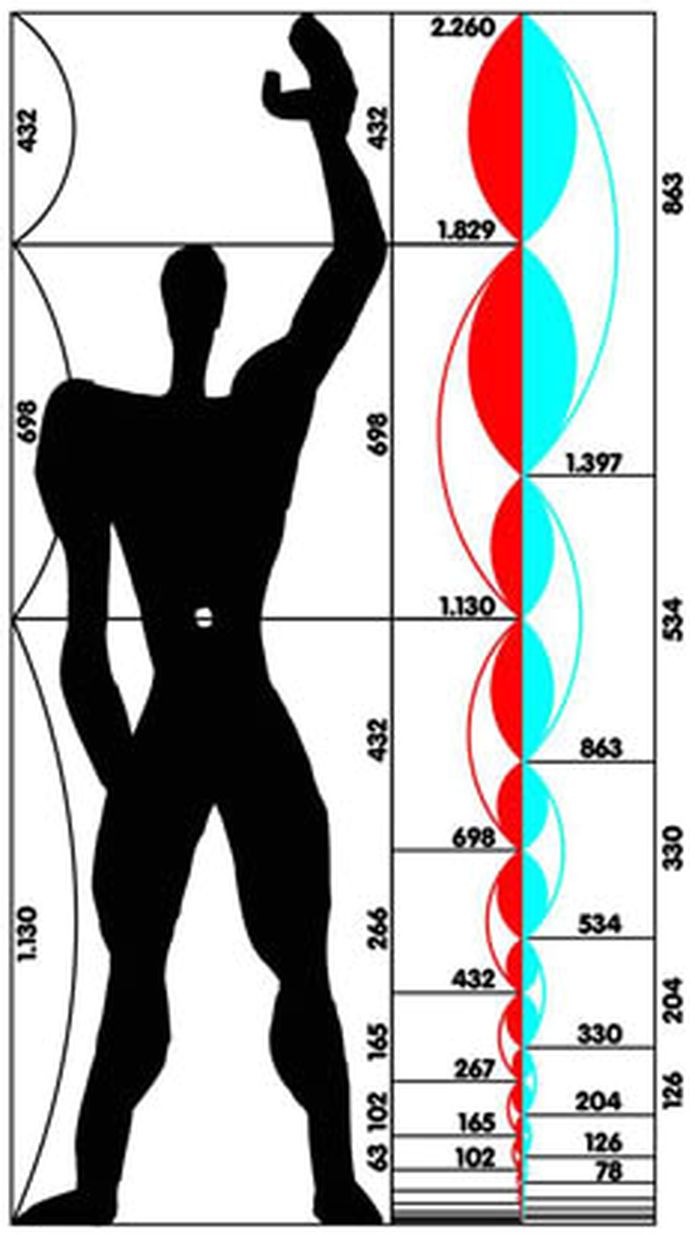 Abb.1 Der Modulor [
Abb.1 Der Modulor [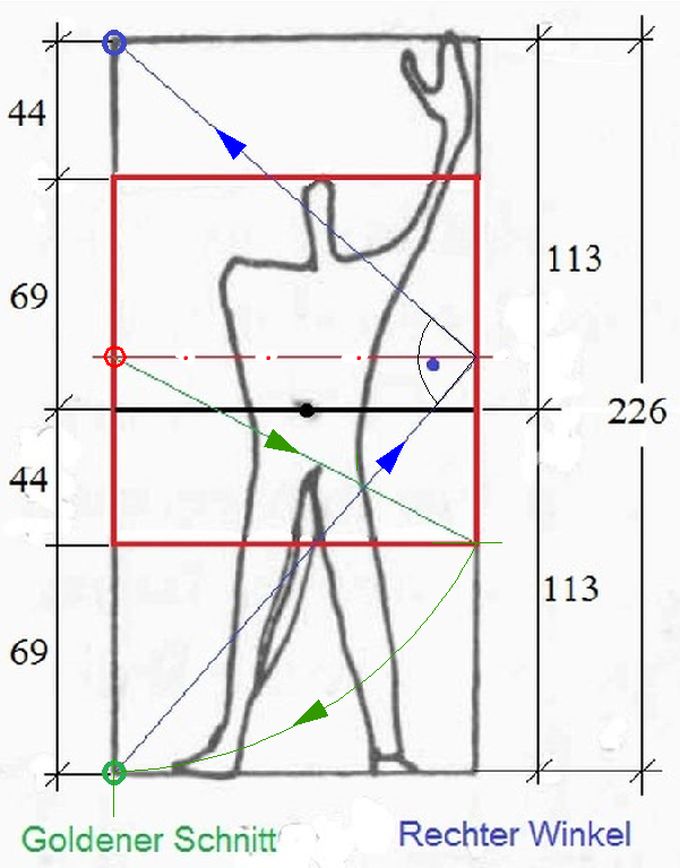 Abb.2 Das "Gitter"
Abb.2 Das "Gitter"