<< Home
<< andere Sonnenuhren-Beiträge
 ↓↓ Ende

Die Zeitgleichung für Nicht-Astronomen

(DGC-Mitteilungen Nr. 111, Herbst 2007)

Inhalt

1. Einleitung  ↑ Anfang

Die Zeitgleichung ist ein astronomisches Problem, das schon Hipparch behandelt hat und im Almagest ziemlich genau und bündig angesprochen ist [6]. Erst im 17.Jahrhundert wurde wieder darüber gearbeitet. Es war der Engländer John Flamsteed, der damit bekannt wurde und zu Ehren kam, indem ihm die Errichtung und Leitung des Observatoriums in Greenwich anvertraut wurde.

In der folgenden Arbeit wird der in der Folgezeit erarbeitete Rechengang für Nicht-Astronomen aufbereitet. Das heisst vor allem, dass zuerst die entsprechenden astronomischen Vorkenntnisse vermittelt werden. Im Einzelnen bedeutet es, auf de aus den beiden ersten Kepplerschen Gesetzen folgenden und in der Keplergleichung enthaltenen quantitativen Zusammenhang einzugehen.

Als Größen-Bezeichnungen und -Symbole werden die im entsprechenden Kapitel im "Sonnenuhren Handbuch", DGC [1] gewählten verwendet, um beide Arbeiten leichter miteinander vergleichen zu können.

In einer älteren Arbeit [2] habe ich mich "elementar" mit der Zeitgleichung befasst. Die Kepler-Gleichumg kommt dabei gar nicht zur Anwendung, sondern die Zeitgleichung wird als Summe von zwei Sinus-Funktionen, die je die Wirkung einer der beiden Zeitgleichungsursachen beschreiben, zusammengesetzt. Dabei wird zudem noch vernachlässigt, dass beide Ursachen, wenn auch nur schwach, nicht voneinander unabhängig sind.
Ganz wesentlicher Unterschied zum strengen Umgang mit dem Phänomen Zeitgleichung ist, dass man ein zeitloses Ergebnis für ein Kalenderjahr mit konstanter und in Tagen ganzzahliger Länge von 365 Tagen gewinnt und dieses in jedem weiteren Jahr wieder benutzt, wobei innerhalb des 4-jährigen Kalenderzyklus für den gleichen Kalendertag ein systematischer Fehler von bis zu einer halben Minute inkaufgenommen wird. Von den zusätzlich bestehenden kleineren himmelsmechanischen Einflüssen, die Jahr für Jahr (die Näherung zwischen Perihel und Frühlingspunkt sogar während eines Jahres) zu berücksichtigen wären, wird sowieso keiner beachtet.
Zu bemerken ist allerdings, dass die in einem einzigen Kalenderjahr "untergebrachte" Zeitgleichung im Zusammenhang mit Sonnenuhren genügt, denn diese lassen sich fast immer nicht genauer als auf die Minute ablesen, und die Teilung der Zeitgleichung in die beiden Anteile ist eine anschauliche Hilfe dafür, sie in etwa zu verstehen.
Weil in dieser vereinfachten Arbeit die Schwankung der Tageslänge ermittelt und daraus auf die Zeitgleichung geschlossen wird, kann der Eindruck entstehen, dass die Drehung der Erde um ihre Achse ungleichmäßig sei. Sie macht zwar den Hauptteil der Tageslänge aus, ist aber sehr gleichmässig und keine Ursache der Zeitgleichung. Die Erddrehung kommt folglich in der folgenden, relativ strengen Behandlung der Zeitgleichung gar nicht vor.
Dass nicht die Erddrehung sondern die Bahnfahrt der Erde um die Sonne zu untersuchen ist, soll auch eine mechanische Nachbildung der ungleichmäßig laufenden kosmischen Uhr zeigen. Es handelt sich um eine übliche 24h- Zeigeruhr, die gerinfügig zu langsam läuft, und der ein relativ aufwändiger Jahresantrieb zugefügt ist.

2. Ein mechanisches Modell der kosmischen Uhr   ↑ Anfang

Unsere mechanischen Uhren und Kalendarien sind Nachbildungen der grossen kosmischen Uhr mit der Sonne als Zeiger. Menschen der Moderne sind mechanische Uhren als "Zeitmacher" [3] inzwischen viel vertrauter als die (scheinbaren) Bewegungen der Sonne. Deshalb seien die kosmischen Verhältnisse einmal umgekehrt mit Hilfe einer solchen Uhr erklärt.

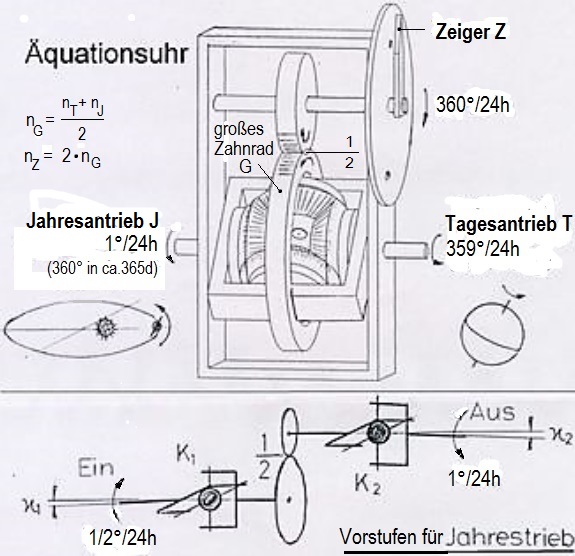
<< Abb.1  Eine Äquationsuhr mit zwei Antrieben bzw.
ein mechanisches Modell der kosmischen Uhr (schematisch)

Eine derartige Uhr (Abb.1) hat zwei Antriebe, die gemeinsam über ein Additionsgetriebe (Umlaufrädergetriebe, Differentialgetriebe) für die Drehung des Stundenzeigers auf einem 24-Stunden-Ziffernblatt ("Grosse" Uhr) sorgen. Der schnellere (Tagestrieb, rechts in der Abbildung) dreht sich um 359° pro 24h. Er repräsentiert den Sternentag (die Erde macht dabei eine 360°-Umdrehung, für den Sonnentag muss sie sich aber etwas weiter drehen). Der langsamere Antrieb (Jahrestrieb, links) macht 1 Umdrehung in 365 Tagen (also 1° pro 24h in etwa, er repräsentiert die Bahnfahrt der Erde um die Sonne mit einmal pro Jahr). Im Getriebe werden die Drehungen beider Antriebe addiert (eine weniger bekannte Anwendung des bekannten Differentialgetriebes) mit dem Ergebnis 360° Umdrehung des Uhrzeigers rechts oben in 24h.

Der Jahrestrieb des Modells hat für die Simulierung des Einflusses der ungleichmäßig verlaufende Bahnfahrt ein vorgeschaltetes Getriebe mit periodischem Übersetzungsfehler (Kreuzgelenk K₁). Der Einfluss der schiefen Position der Drehachse der Erde auf der Ebene Ihrer Bahnfahrt um die Sonne (zweite Zeitgleichungsursache) hat mit der Ungleichmäßigkeit der Banhnfahrt an sich nichts zu tun. Das entsprechende Getriebe mit ebenfalls einem periodischen Übersetzungsfehler (Kreuzgelenk K₂)zum Simulieren dieses Einflusses könnte jedem der beiden Antriebe vorgeschaltet werden. Gewählt ist, es als zweites dem ersten im Jahresantrieb vorzuschalten (beide in Reihe nacheinander). Ergebnis ist eine die Wahre Sonnenzeit anzeigende, sogenannte Äquationsuhr. Im Anhang 1 ist die Konstruktion des Jahrestriebs von Abb.1 näher erläutert. Die Reihenschaltung zweier Getriebe mit periodischem Übersetzungsfehlern passt zu einer angenäherten Zeitgleichung, die lediglich durch Superposition von zwei periodischen Ausdrücker besteht [2].

3. Vorgehen   ↑ Anfang

Zum Verständnis der Zusammenhänge, die zur Zeitgleichung führen, muss vom heliozentrischen Weltbild ausgegangen werden. Bei geozentrischer Betrachtung ist die erste Ursache der Zeitgleichung, nämlich die Bahnfahrt der Erde auf einer Ellipse nicht erkennbar und quantitativ nicht beschreibbar. Mit Hilfe der Kepler-Gleichung ist die Zeitfunktion des Ortes der Erde auf ihrer Bahn, die sogenannte wahre Anomalie (eine von Kepler eigeführte Größe) zu gewinnen. Letztere kann nach dem Wechsel zu geozentrischer Betrachtung als ekliptikale Länge der Sonne in Abhängigkeit von der Zeit gedeutet werden. Der Systemwechsel bedeutet nämlich, dass die Sonne an die Stelle der Erde tritt.

Bei der Beobachtung der ekliptikalen Bewegung der Sonne von der Erde aus stört deren Drehung (Tagestrieb). Man muss sich die Drehung der Erde auf 1U/Jahr reduziert denken oder sich gedanklich als Mitfahrer im drehenden Koordinatensystem der Ekliptik empfinden.

Der ekliptikalen Länge der Sonne entspricht im ebenfalls drehenden Koordinatensystem des Äquators ihre Rektaszension α(t), die die Wahre Sonnen- oder Ortszeit repräsentiert (bei der Vorstellung 1U/Jahr der Erde sind diese beiden Koordinatensysteme Erd-fest.). Sie ist der Subtrahend in der Zeitgleichung, die wie folgt definiert ist:

(1)   ZG(t) = (4 min/°)·(α_M(t) - α(t)) [1].

Der Minuend ist α_M(t), die Rektaszension einer gedachten, gleichmässig übers Jahr auf dem Äquator umlaufenden Vergleichs-Sonne (sogenannte mittlere Sonne mit mittlerer Rektaszension), die die Mittlere Sonnen- oder Ortszeit repräsentiert. Bei einer Winkel-Differenz (α _M - α) von 2π beziehungsweise 360° hätte die Zeitgleichung einen Wert von 24 Stunden. 1° entspricht somit 4 Minuten.

Die Definition mit Ortszeiten ist ZG = WOZ – MOZ. Die Vorzeichen-Umkehr gegenüber Gl. (1) (α_M entspricht der mittleren Ortszeit MOZ, α der wahren WOZ) kommt von der unterschiedlichen Richtungswahl für Rektaszension α und Stundenwinkel τ (Maß für Ortszeiten).

Die ursprüngliche Definition enthielt die umgekehrte Differenz und lautete ZG = MOZ – WOZ. Darin ist die mittelalterliche Bedeutung vom heute noch gebrauchten Wortteil “-Gleichung” als “eine Korrektur zufügen” zu erkennen. Man hatte der wahren Sonnenzeit die Differenz zur mittleren Sonnenzeit hinzuzufügen, um zu letzterer zu gelangen:
MOZ = WOZ + ZG [7].

4. Heliozentrische Betrachtung    ↑ Anfang

Jahrestrieb der kosmischen Uhr sei vorerst nur die elliptische Bahnfahrt der Erde als erste Ursache der Zeitgleichung. Der Einfluss ihrer speziellen Lage der Erdachse (zweite Ursache) wird später berücksichtigt. Mittelpunkt der Ellipse ist 0 (Abb.2). In einem ihrer beiden Brennpunkte B befindet sich die Sonne. Perihel P und Aphel A sind die Scheitelpunkte der Bahnellipse. X ist der Ort der Erde in einem bestimmten Moment t, ausgedrückt durch den Winkel wahre Anomalie V(t).

4.1 Die mittlere Anomalie   ↑ Anfang

Eine fiktive sogenannte mittlere Erde (Pendant zu einer sogenannten mittleren Sonne) befinde sich bei Y, was mit dem mittlere Anomalie genannten Winkel M(t) angegeben werden kann:

(2)   M(t) = (2π/J_an) (t-t_P).

Der Winkel M(t) ist "eine normalisierte Zeit" [9]. Seine gleichmäßige Vergrößerung macht in einer graphischen Darstellung (Abb.2) den gleichmässigen Ablauf der Zeit sichtbar. Y ist somit die Spitze eines gleichmässig drehenden Zeigers (Vektors). Dieser dient für den Ortsvergleich mit dem mit der wahren Erde X verbundenen Vektor, der nicht gleichmässig dreht. Die Drehung am Eingang des Jahrestriebs (Abb.1) ist wie M(t) gleichmässig. Aus konstruktiven Gründen (Anhang 1) ist die Winkelgeschwindigkeit der Eingangs-Welle aber vorerst halbiert.

Die Perihel-Passage der Erde ist als Beginn des anomalistischen Jahres J_an definiert. Auf den entsprechenden Zeitpunkt t_P bezieht sich auch die mittlere Anomalie: Die fiktive mittlere Erde passiert das Perihel P praktischerweise zur gleichen Zeit, und gemäß zweitem Keplerschen Gesetz treffen sich beide Erden dann auch im Aphel A.

Dass die mittlere Anomalie M eine lineare Funktion der Zeit t ist, wird mit dem geraden Graph in Abb.2, links unten angedeutet.

Bei der Zeitgleichung ist der etwa 3 Tage vor der Perihel-Passage liegende 1. Januar (12:00 Greenwich Time) als t_K zeitlicher Bezugspunkt. In die Gleichung (2) ist der konstante Winkelwert M₀ (repräsentiert t_K-t_P) einzufügen:

(2a)  M(t) = M₀ + (2π/J_an) (t-t_K).

M₀ ist negativ und eine Jahreskonstante, hat also jedes Jahr - vor allem aber in den vier aufeinander folgenden Jahren einer Schaltperiode - einen anderen Wert. Die M₀-Veränderlichkeit ist grundsätzlich nur von Bedeutung, wenn man die mit guter Näherung "zeitlos" gültige Zeitgleichung später mit zum Jahr innerhalb des Schaltrhythmus passendem und mit evtl. aktuell genauerem Wert (zusammen mit aktuell besseren Werten anderer Jahreskonstanten) mit der aktuell besten Genauigkeit erneut starten will. Die in Astronomischen Jahrbüchern jährlich neu veröffentlichten Zeitgleichungstabellen sind das Ergebnis solchen Vorgehens.

4.2 Die Kepler-Gleichung   ↑ Anfang

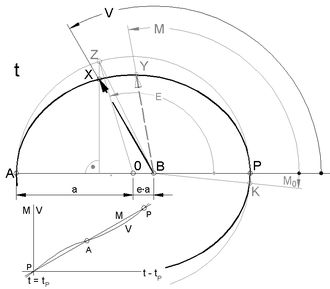
<< Abb.2  Erdbahn-Ellipse

Der Zusammenhang zwischen wahrer V(t) und mittlerer M(t) Anomalie wird nach einem Zwischenschritt erkennbar, nämlich nach der Einschaltung der Kepler-Gleichung, der von Kepler selbst vorgenommenen mathematischen Formulierung seines 2. Gesetzes (das 1. Gesetz postuliert die Ellipsenform der Bahnen der Himmelskörper und ist bereits vorgegebene Bedingung):

(3)   M(t) = E(t) – e·sin E(t)   (Anhang 2).

Dabei ist die Zwischengröße E ebenfalls eine Anomalie (mit der Zeit veränderlicher Winkel), nämlich die exzentrische. Man beachte, dass sich der Scheitel ihres Winkels im Zentrum 0 der Ellipse befindet (Abb.n 2 und 8), sie aber von Kepler exzentrische Anomalie genannt wurde.

Gleichung (3) nach E(t) aufzulösen, ist in geschlossener Form nicht möglich. Es gelingt aber z.B. mit Hilfe des bekannten Newton'schen Näherungsverfahrens, das jener für diesen Zweck erfand, und das zu einem wichtigen Verfahren der numerischen Mathematik wurde.

V(t) in Abhängigkeit von E(t) ist dagegen ein einfacher geometrischer Zusammenhang innerhalb der Ellipse, wobei vom Mittel- (O) zum Brennpunkt (B) zurück gekehrt wird:

(4)   tan(V(t)/2)= κ·tan(E(t)/2)   (Anhang 3).

κ ist eine Ellipsen-Konstante, ausgedrückt mit der relativen (numerischen) Exzentrizität e der Ellipse:  κ = ((1+e)/(1-e))^1/2

Der Graph V(t) deckt sich erwartungsgemäss nicht mit dem Graph M(t) (Abb.2, links unten).

Die erste Ursache der Zeitgleichung ist nunmehr erfasst.

5. Übergang zu geozentrischer Betrachtung (Abb.3)   ↑ Anfang

Abb.3 zeigt, was jeweils ein Sonnen- und ein Erdbewohner sehen kann. Die Beobachtungen beginnen beim Periheldurchgang der Erde. Von der Sonne aus sieht man die Erden nach links laufen, den Gegenpunkt (F) zum Widderpunkt passieren und die Orte Y und X zum Zeitpunkt t erreichen. Der bis X überstrichene Winkel ist V = (Λ) - (L) (Abb.2, (L) hat negativen Wert). Der Erdenbewohner sieht (bei 1U/Jahr der Erde um ihre Achse) die gleiche Bewegung, nur sind ihr anstatt der Erden X und Y die Sonnen S und S' (wahre und fiktive mittlere Sonne) unterworfen. Diese laufen ebenfalls nach links und über F (Frühlings- gleich Widderpunkt) hinaus bis zu den Punkten S' und S, die sie im Zeitpunkt t einnehmen. Die Winkelvergrösserung bis S ist wieder Λ - L.

Die mit V = (Λ) - (L) bereits vorgenommene veränderte Wahl des Nullpunktes von P nach (F) entspricht dem astronomischen Brauch, als Nullpunkt im geozentrischen System den Frühlingspunkt F zu wählen. Damit ist die eklipikale Länge Λ der wahren Sonne:

(5)   Λ(t) = V(t) + L(t).

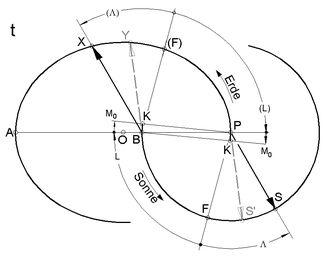
<< Abb.3  Erdbahn-Ellipse und Sonnenbahn-Ekliptik

Die Drehung V(t) bzw. Λ(t) wird vom kleineren Zahnrad in der Mitte des Jahrestriebs (Abb.1: Stufe 1/2) nachgebildet.

V(t) kommt aus Gleichung (4). L(t) ist die ekliptikale Länge des Perihels, deren schwache Änderung permanent berücksichtigt wird. Das Perihel nähert sich dem Punkt (F) mit

(6)   L(t) = L₀ + (pf/J_tr)·(t-t_P),   wobei L₀ die Jahreskonstante ist.

Das Zusammenrücken beträgt ca. 0,0172°/J_tr. Es wird von der Drehung der Apsidenlinie der Erdbahn verursacht. Deshalb ist das tropische Jahr J_tr etwas kürzer als das anomalistische J_an. Beide Jahrlängen sind in der Konstante pf wie folgt enthalten: pf = 2π(1 - J_tr/J_an).

Ohne sofortige Berücksichtigung des Zusammenrückens, d.h. mit

(6a)  L(t) = L₀       (Werte von L(t) und L₀ negativ)
ist die Auswirkung auf die Zeitgleichung über ein Jahr nicht gvrößer als 3,5 Sekunden.

In Abb.3 ist die Sonnenbahn ausdrücklich als Kreis gezeichnet. Es handelt sich um die Ekliptik (s. auch Abb.4). Die drehenden Vektoren haben ihre Spitzen jetzt bei S und S'.

6. Geozentrische Betrachtung, Zeitgleichung (Abb.4)    ↑ Anfang

Der "Ablauf" der Tageszeit wird hauptsächlich durch die Eigendrehung der Erde (Tagestrieb) verursacht, die auf dem Himmels-Äquator messbar ist, weshalb auch in der Zeitgleichung Bahnstücke auf dem Himmels-Äquator zu verrechnen sind. Von den beiden poraren Koordinaten der Sonne interessiert nur die Rektaszension α, nicht die Deklination (Höhenwinkel δ). Wegen der Winkellage (ε) zwischen Äquator- und Ekliptik-Ebene (die zweite Ursache der Zeitgleichung) ist die Übertragung der ekliptikalen Länge Λ der wahren Sonne auf ihre äquatoriale Rektaszension übers Jahr unterschiedlich.

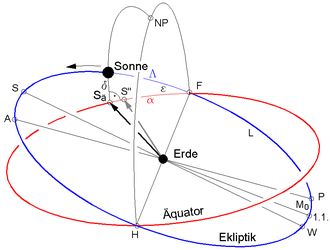
<< Abb.4  Ekliptik und Himmels-Äquator

Die wahre Sonne wird von der Ekliptik zum Punkt S_ä auf den Äquator "herunter geholt". Vom Punkt S_ä wird jetzt ein Vektor in der Äquatorebene bewegt ( Anhang 4 ). Seiner doppelt ungleichmässigen (ungleichmässige Bewegung der wahren Sonne auf der Ekliptik, die ungleichmässig in seine Bewegung auf dem Äquator umgewandelt wird) entspricht schliesslich die Drehung der Ausgangs-Welle im Jahrestrieb (Abb.1). Beigesellt ist in Abb.4 der Vergleichsvektor, der zu einer weiteren, einer zweiten mittleren Sonne, dem fiktiven Punkt S'' zeigt.

Die Umrechnung zwischen ekliptikalen und äquatorialen Koordinaten ist z.B. mit den bekannten Transformations-Gleichungen oder mit folgender einfachen Beziehung im rechtwinkligen sphärischen Dreieck Sonne/S_ä/F möglich:

(7)   α(t) = arctan ( tan Λ(t) · cos ε ).

Gleichung (7) liefert den Subtrahend von (1).

Der Minuend α_M(t) ist die Rektaszension der Bezugs-Sonne S'', die auf dem Äquator gleichmässig umläuft:

(8)   α_M(t) = α₀ + (2π / J_tr) (t-t_K).

(9)   α_M(t) = M₀+ L₀ + (2π / J_tr) (t-t_K)

mit α_M(t=t_K)=α₀=M₀+L₀. Zur Erinnerung: M₀ und L₀ haben negative Werte.

Die zweite Ursache der Zeitgleichung ist jetzt auch erfasst. Nachdem die Gleichungen (7) und mit (9) in Gleichung (1) eingesetzt worden sind, ist die Zeitgleichung in der gewünschten Strenge gefunden.

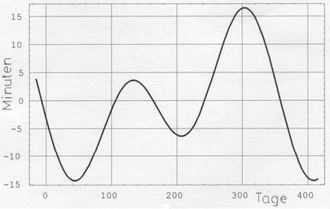
<< Abb.5  Zeitgleichung als Graph

Die Einführung der fiktiven Sonne S'' war aus anschaulichen Gründen nötig, um Bahnstücke auf dem Himmels-Äquator gegeneinander verrechnen zu können, wie oben (Anfang des Abschnitts) gefordert wurde. Es zeigt sich aber, dass die Rechnung formal auch richtig ist, wenn man die Bewegung der fiktiven Sonne S' zum Vergleich heran zieht. Beide Sonnen passieren gemäß Vorgabe den Frühlingspunkt gleichzeitig, und als Repräsentanten des gleichmäßigen Ablaufs der Zeit sind ihre Bewegungsgeschwindigkeiten grundsätzlich gleich groß. Es spielt wertmäßig keine Rolle, dass beide Sonnen auf unterschiedlichen Bahnen (S' auf der Ekliptik, S'' auf dem Äquator) laufen und ihre momentanen Winkel verschiedene Namen (ekliptikale Länge für S', Rektaszension für S'') haben. Dieser eigentlich leicht einsichtige Zusammenhang wird dennoch im Anhang 5 nochmals formal hergeleitet, indem durch Gegenüberstellen bisher verwendeter Gleichungen die Aussage gewonnen wird, dass die Rektaszension der mittleren Sonne S'' zu jeder Zeit gleich der ekliptikalen Länge der mittleren Sonne S' ist, die die mittlere Anomalie M(t) repräsentiert [1] (im Original Rektaszension der mittleren Sonne und ekliptische Länge des Punktes Y).

Für die Zeitgleichung, um die es letztlich geht, ist in der Literatur folgende kuzgefasste Aussage zu finden:
"Die Differenz mittlere Sonnenzeit minus wahre Sonnenzeit oder Rektaszension der wahren Sonne minus Rektaszension der mittleren Sonne heisst Zeitgleichung ... ." [4].

7. Die Zeitgleichung über ein Jahr und mehr (mit Rechenbeispielen)   ↑ Anfang

Die Graphen von Minuend und Subtrahend der Zeitgleichung sind wie die beiden Linien in Abb.2 (links unten) stetig ansteigend, was schon auf den ersten Blick nicht auf eine Jahres-Periodizität hinweist. In der Gleichung ist t-t_k in Tagen einzusetzen. Sie beginnt im Zeitpunkt t=t_k am 1.Januar 12^h mittags in dem Jahr, dessen Jahres-Konstanten M₀ und L₀ in ihr enthalten sind, und kann viele Jahre lang benutzt werden.

<< Abb.6  Sonnenuhr in Chur/CH
Zeitgleichung über 12 Monate und mit umgekehrten Vorzeichen gegenüber Abb.5 (alte Definition: s. 3.)

Der Zeitpunkt t-t_k = 364 (365 in einem Schaltjahr) ist der Mittag des 31. Dezember im ersten Jahr, t-t_k = 365 (366) ist der 1. Januar des nächsten Jahres usw. Man kann die Gleichung für jeden (t-t_k)-Wert, also über Jahre hinweg benutzen. Die in den Abbildungen 5 und 6 in Näherung erkennbare Periodizität ist aber streng weder ans tropische Jahr J_tr noch ans anomalistische J_an gebunden. Wegen der Annäherung zwischen Frühlingspunkt und Perihel ändert sich die Kurvenform auch langfristig. Innerhalb einer Schaltjahrperiode sind die Werte von Kalenderjahr zu Kalenderjahr auf der Zeitachse 3 mal ca.1/4Tag vor-, am Ende ca.3/4Tag zurück verschoben, was mit der Jahreskonstante M_o erzeugt wird, wenn man für jedes der vier Jahre eine separate Rechnung anstellt. Im fünften Jahr ist die Kurve der vom ersten Jahr gleich, wenn M₀ nicht auf Grund neuester Messungen korrigiert wurde.

Für wissenschaftlich/technische Anwendungen der Zeitgleichung, wozu ihr Gebrauch bei der Sonnenuhr nicht zählt, wird sie noch genauer als hier beschrieben berechnet. Die erste höheren Stufe ist die Ermittlung einer neuen Gleichung ab 1.Januar des nächsten Jahres mit Hilfe anderer Jahres-Konstanten M₀ und L₀ und sich sehr langsam ändernden Werten für Jahreslängen J_tr und J_an , relative (numerische) Exzentrizität e der Erde und Schiefe der Ekliptik ε [1]. Dabei können die auf astronomischen Messungen beruhenden Prognosen in der Zwischenzeit verbessert worden sein (gilt auch für M₀ und L₀).

Zu berechnen ist die Zeitgleichung für 1.November 2014, 12:00 UT (t'= (t-t_K) = 305 Tage)  und  2.April 2015 (t' = 456 Tage)

Diesjährige (Jahr 2014) Basis-Werte [1]:

M₀ = -2,11463°
J_an = 365,259988 Tage
J_tr = 365,242901 Tage
e = 0,0167031
ε = 23,437470°
L₀ = -76,81929°

Zwischenrechnungen:

(2a)  M(t') = M₀ + (360°/J_an) (t-t_K)         = 298,493173°       = 87,318675°
(3)   M(t') = E(t') – e·sin E(t')   →   E(t')  = 297,645412°       = 88,275259°
     κ = ((1+e)/(1-e))^1/2 = 1,016845
(4)   tan(V(t)/2)= κ·tan(E(t)/2)   →   V(t') = 296,794308°       = 89,232127°
     pf = 360°(1 - J_tr/J_an) = 0,0168343°
(6)   L(t') = L₀ + (pf/J_tr)·(t-t_K)                = -76,805232°        = -76,798273°
(5)   Λ(t') = V(t') + L(t')                        = 219,989076°        = 12,434154°
(7)   α(t') = arctan ( tan Λ(t') · cos ε )    = 217,580844°        = 11,436463°
(9)   α_M(t') = M₀+ L₀ + (360° / J_tr) (t-t_K) = 221,687941°        = 10,520402°
Bemerkungen: Mit Wert >360° errechnete Winkel müssen um 360° oder um das Vielfache von 360° verringert werden.
                      Mit arctan negativ erhaltene Winkel müssen um 180° oder um das Vielfache von 180° auf positive
                      Werte erhöht werden.

Ergebnisse:

(1)   ZG(t') = (4 min/°)·(α_M(t') - α(t'))      = 16,428388 min = 16 min 26 sec     = -3,664244 min = -3 min 40 sec

8. Vergleich mit vereinfachenden Betrachtungen↑ Anfang

erste Ursache (elliptische Erdbahn):

Die ungleiche Bahngeschwindigkeit der Erde, beschrieben mit dem zweiten Kepler'schen Gesetz wird mit der Kepler'schen Gleichung (3) berücksichtigt, die in die Gleichung (4) für die wahre Anomalie der Erde eingeht. Die Zeitgleichung hätte folgende Gestalt, wenn die Sonne auf dem Himmels-Äquator umliefe, nur die elliptische Form der tatsächlichen Erdbahn zu berücksichtigen wäre.

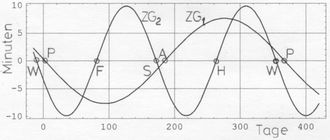
<< Abb.7  Zeitgleichung, getrennt in 2 Teil-Graphen

ZG₁(t) = (4 min/°)·(M(t) – V(t)) (Abb.7).

Dieser mit dem anomalistischem Jahr periodische Ausdruck hat seine Nullstellen in Perihel (P) und Aphel (A). Er ähnelt z.B. ZG1 in [2]. Die Amplitude ist hier 7,66min, dort 7,65min.

zweite Ursache (Neigung der Erdachse):

Aus der wahren Anomalie der Erde wird mit Gleichung (5) die zugehörende ekliptikale Länge der wahren Sonne bestimmt. Die Bewertung des Ortes der wahren Sonne hat aber in Bezug auf den Himmelsäquator zu geschehen (Abschnitt 6, 1. Absatz). Mit Gleichung (7) wird die wahre Sonne auf den Äquator "herunter geholt", indem ihre Rektaszension bestimmt wird. Die Zeitgleichung hätte folgende Form, wenn die Erdbahn ein Kreis wäre, nur die Neigung der Erdachse berücksichtigt werden müsste.

ZG₂(t) = (4 min/°)·(α_M(t) - α_S'(t)) (Abb.7).

α_S'(t)ist die Rektaszension der ersten mittleren Sonne S'. Sie wird durch Einsetzen von M(t) an Stelle von V(t) in Gleichung (5) (mit L(t)=L_o) und Weiterrechnen mit Gleichung (7) ermittelt.

Der mit dem halben tropischen Jahr periodische Ausdruck ZG₂ hat seine Nullstellen annähernd in den Solstitien (W und S) und in den Äquinoktien (F und H). Er ähnelt z.B. ZG2 in [2]. Seine Amplitude ist hier 9,86min, dort 9,83min.

Analog dem Vorgehen in [2] lassen sich auch die beiden Graphen aus Abb.7 addieren und eine Annäherung an den Graphen von Abb.5 finden (Anhang 6).

9. Literatur   ↑ Anfang

[1] Deutsche Gesellschaft für Chronometrie: "Sonnenuhren Handbuch", 2006
[2] S.Wetzel: "Eine elementare Behandlung der Zeitgleichung", DGC-Mitteilungen Nr.109, 2007
[3] E.M.Fürböck: "Gedanken über das Wesen der Räderuhr", Schriften der Freunde alter Uhren, 1977
[4] "Physikalisches Wörterbuch" (Herausgeber Wilhelm H. Westphal), Verlag Springer, 1952
[5] S.Hildebrand: "Feinmechanische Bauelemente", Berlin und München, 1968, Seite 725
[6] R.Wolf: "Handbuch der Astronomie", Amsterdam 1973
[7] N. Dershowitz, E.M. Reingold: "Calendrical Calculations", Cambridge University Press, 2008
[8] Thoos, Schmelz, Auktor: "Gelenke und Gelenkwellen", Springer, 2002, Seiten 5 und 6
[9] R. Strebel: "Die Keplersche Gleichung", Berichte über Mathematik und Unterricht,
     Eidgenössische Technische Hochschule Zürich, 2001, Seite 11
[10] M. Ohm: Lehrbuch der gesamten höheren Mathematik, Leipzig 1839, Bd.1, S.271
[11] O. Montenbruck: "Grundlagen der Ephemeridenrechnung." 7. Auflage. Spektrum Akademischer Verlag,
       Heidelberg 2005.

10. Anhänge   ↑ Anfang

Anhang 1: Oszillierender Jahrestrieb (Abb.1)   ↑ zurück

Konstruktionsvorschlag, von einem gleichförmigen Antrieb (Motor) ausgehend:

Motor (1U / 730,5Tage = ½ U / Jahr) — Kreuzgelenk K₁ ("Kardangelenk", Knickung der Achsen κ₁=20,7°) — Rädergetriebe (Übersetzung 2:1 ins Schnelle >> 1U / Jahr)) — Kreuzgelenk K₂ (Knickung κ₂=23,5°) — [Additionsgetriebe]

Der durch Achs-Knickung entstehende periodische Übersetzungsfehler hat gegenüber der Achsendrehung doppelte Frequenz. Weil die Folge aus der 1.Ursache in der Zeitgleichung einfache Jahres-Frequenz hat, wird mit halber Antriebsdrehzahl begonnen und nach dem 1.Kreuzgeklenk eine 2:1-Übersetzung (ins Schnelle) eingeschoben. Die Folge aus der 2.Ursache hat doppelte Jahresfrequenz, wozu die Fehlerfrequenz des folgenden 2.Kreuzgelenkes jetzt passend ist. Die Knickung ist bei beiden Gelenken gleichsinnig, wodurch sich die Fehler addieren. Wegen der Zeitdifferenz zwischen Perihel- und Wintersolstitium-Durchgang der Erde befinden sich aber die beiden Gelenk-Knicke nicht genau in derselben Ebene.

Anhang 2: Kepler'sche Gleichung (Abb.8)     ↑ zurück

Die Kepler'sche Gleichung (3) verknüpft die beiden Anomalien E und M miteinander, bzw. führt zu einer Funktion E(t). In Abb.8 sind die Verhältnisse im Unterschied zu Abb.2 auf die große Halbachse der Ellipse normiert (große Halbachse und Umkreisradius = 1).Die Gleichung (3) ist wie folgt zu finden:

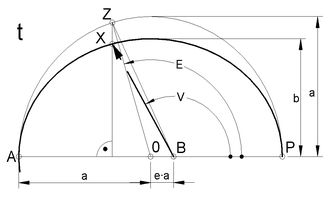
<< Abb.8  Ellipse mit Umkreis

Bei der Bewegung der Erde von P nach X überstreicht der Fahrstrahl B→X die Fläche XBP. Ihr entspricht auf dem Umkreis die Fläche ZBP, die mit der exzentrischen Anomalie E (ein Winkel) und der numerischen Exzentrizität e (eine Strecke) ausdrückbar ist:

F_ZBP = F_Z0P – F_Z0B.

Mit  F_Z0P = (a²/2) E  (ein Kreissektor) und
mit  F_Z0B = (a²e/2) sinE  (eine Dreiecksfläche) ist
F_ZBP = (a²/2) (E-esinE).

Die vom Fahrstrahl B→P überstrichene Fläche  F_XBP  ist um den Stauchungsfaktor b/a
zwischen Umkreis und Ellipse kleiner als die Fläche F_ZBP:
F_XBP = (b/a) F_ZBP.

Gemäss zweitem Kepler'schem Gesetz sind die Verhältnisse zwischen überfahrenen Flächen und zwischen den dazu benötigten Zeiten gleich.

F_XBP / F_Ellipse = (t-t_P) / J_an.

(2π/J_an) (t-t_P) = E - e sinE .

Die linke Seite ist die normalisierte Zeit [9], die Kepler den Winkel mittlere Anomalie M(t) (s. Gl.(2)) genannt hat.

Somit ist die (mit der Zeitabhängigkeit ergänzte) Kepler-Gleichung hergeleitet:

(3)   M(t) = E(t) – e·sin E(t), qed.

Anhang 3: Von Anomalie E zu Anomalie V    ↑ zurück

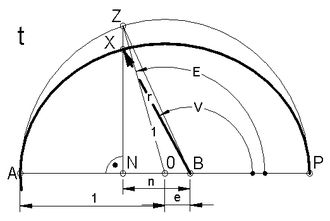
Die Polargleichung einer Ellipse mit Einheits-Umkreis, mit B als Pol, BP als Polarachse und V als Parameter lautet bekanntlich [10]:

(10)   r = (1-e²)/(1+e·cosV) ,     und in anderer Schreibweise:
(11)   r(1+e·cosV) = (1–e²).

Weiter mit einer Fleissarbeit in mehreren Schritten:

Dreieck 0NZ:  n-e = cos(π-E) = -cosE,
Dreieck BNX: n = r·cos(π-V) = -r·cosV, Eliminieren von n:
(12) r·cosV = cosE–e,
(12) in (11) >> (13) r = (1–e·cosE),
(13)+(12) >> (14) r(1+cosV) = (1–e)(1+cosE),
(13)–(12) >> (15) r(1–cosV) = (1+e)(1–cosE),
(14)/(15) >> (16)
(16) (1+cosV)/(1–cosV) = (1–e)(1+cosE)/((1+e)(1–cosE)).

Mit den Identitäten (s. in einer Formelsammlung)
1+cosα = 2cos²(α/2) und 1-cosα = 2sin²(α/2):

(16) sin²(V/2)/cos²(V/2) = ((1+e)/(1-e))(sin ² (E/2)/cos²(E/2)),
(17) tan(V/2)=((1+e)/(1–e))^1/2tan(E/2).

Unter Beachtung der Zeitabhängigkeit und mit κ für den Wurzelausdruck ist das Gleichung

(4)   tan(V(t)/2) = κ·tan(E(t)/2), qed.

Anhang 4: Kinematische Analogie zwischen "Herunterholen der Sonne"und einem Kreuzgelenk   ↑ zurück

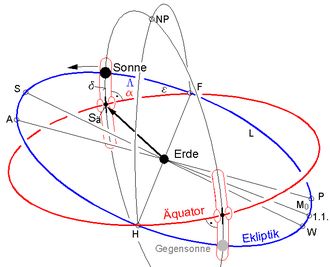↑ ↑ Abb.4a  "Herunterholen der Sonne auf den Äquator"
<< Abb.10   Kreuzgelenk mit Dreh/Schiebe-Stiftpaar,
                     rote und blaue Gerade: gekreuzte Achsen
                     im Inneren des Gelenkes → Kreuz - Gelenk

Das "Herunterholen der Sonne" auf den Äquator" wird in der Äquationsuhr (Abb.1) vom Kreuzgelenk K₂ simuliert.
Die Analogie zwischen diesem Vorgang und der Bewegung in einem Kreuzgelenk wird in den Abbildungen 4a und 10 deutlich. Gegenüber Abb.4 enthält Abb.4a einen Bügel, der auf dem Äquator gleiten kann und die auf der Ekliptik gleitende Sonne einschließt (ein zweiter Bügel umschließt die Gegensonne). Die Sonne bewegt mit Hilfe dieses Bügels auf dem Äquator den Punkt S_ä, bis zu dem der Rektaszensionswinkel α der Sonne reicht.
Im in Abb.10 gezeigten Kreuzgelenk minimaler Bauart entsprechen dem auf dem Äquator gleitend gedachtem Bügel der Schlitz in der weißen Kugel und der Sonne ein vom Schlitz eingefasster Stift (ein zweiter Stift ersetzt die Gegensonne). Die Stifte bewirken bei gleichmäßigem Umlauf auf dem Ekliptikkreis den ungleichmäßigen Umlauf der Schlitze auf dem Äquator.

Der Vergleich zeigt, dass für das Kreuzgelenk die Gleichung (7) auch gilt:

α → Winkel φ₂ der getriebenen Welle (mit Schlitzen verbunden),
Λ → φ₁ der treibenden Welle (mit Stiften verbunden),
ε → Kippwinkel β zwischen den Wellen.

(7)   α(t) = arctan ( tan Λ(t) · cos ε )       >>>       (7a)  φ₂ = arctan ( tan φ₁ · cos β ).

Kreuzgelenk und Subsolarer Punkt:

Im Kreuzgelenk (Abb.10) laufen die beiden Kreise (roter Kreis auf weißer Kugel und mit 
den Stiften fest verbundener blauer Ring) mit. Die weiße Kugel ist nicht das 
vergrößerte Modell der "stillstehend" angenommenene Erde (zusammen mit ihrem 
Äquator eine gleichmäßige Drehung um die eigene Achse pro Sonnnenjahr). 
Folglich ist es nicht möglich, die Wanderung des mittäglichen Subsolaren Punkts 
auf der Erdoberfläche in einem einfachen Modell mit Hilfe eines Kreuzgelenkes 
darzustellen (vgl. Kreuzgelenk, Sonnenuhr und Zeitgleichung, 
3. und 5. Analemma-förmige Figur und Kreuzgelenk). 
Das ungleichmäßige Drehen der gegen die Antriebswelle gekippten Abtriebswelle 
bei gleichmäßigem Drehen der Antriebswelle ist aber die Analogie dazu, dass 
die sich auf der Ekliptik angenommen gleichmäßig wandernde, "auf den Äquator 
herunter geholte" Sonne (hier Punkt Sä) ungleichmäßig bewegt: zu langsam bei 
Frühlings- und Herbstpunkt (F und W), zu schnell bei Sommer- und Winterpunkt 
(S und W). Etwa 1½ Monate nach diesen Punkten ist sie etwa  2,5° gegenüber der 
gleichmäßig laufenden Sonne S'' (Abb.4) zurück geblieben  bzw. ihr voraus geeilt.


Ergänzende Bemerkungen zum Kreuzgelenk:

Im Vergleich zur Standart-Bauart mit zwei Gabeln (Abb.1) enthält die gezeigte 
minimale Bauart nur eine Gabel. Anstatt zwei Dreh-Stiftpaaren gibt es ein 
Dreh/Schiebe-Stiftpaar, wodurch das namengebende Kreuz mit zwei Drehachsen 
als Zwischenelement entfällt. Das Schieben im kreisförmigen Schlitz ist 
identisch mit dem Drehen um die auf dem Schlitzkreis senktrechte Mittellinie 
(Abb.9: rote Gerade).  
Vergleich von Gleichung (7a) mit entsprechenden Gleichungen in der 
einschlägigen Literatur [8]:
Gleichung (7a) gilt für die sogenannte "rechtphasige" Anfangslage: 
Die Winkel φ1 und φ2 werden von einer Linie aus gezählt, die 
senkrecht auf der von den beiden Wellen gebildeten Ebene wie 
in Abb.10 steht (entsprechende Linie in Abb.4a zwischen H und F). 
Bei sogenannter "nullphasiger" Anfangslage (Bezugslinie liegt 
in der von den Wellen gebildeten Ebene) gilt Gleichung (7b): 
(7b)  φ2 = arctan ( tan φ1 / cos β ). 

Anhang 5: ekliptikale Länge der mittleren Sonne S' gleich Rektaszension der mittleren Sonne S''   ↑ zurück

Die Verwendung von S' als Vergleichszeiger erinnert an die heliozentrische Wirklichkeit. S' repräsentiert Y, die fiktive Erde, deren ekliptikale Länge aus Abb.2 ablesbar ist:

(18)   Λ(t)=L(t)+M(t).

Die vorhergesagte Gleichheit von (18) und (9) wird von nachfolgender Kontrolle bestätigt:

Mit den Gleichungen (6) und (2) wird Gleichung (18) zu (18a):

(18a)  Λ(t) = L₀ + (pf/J_tr)·(t-t_K) + M₀ + (2π/J_an)·(t-t_K).

Mit pf = 2π(1 - J_tr/J_an) (s.5.) entsteht Gleichung (18b), die mit Gleichung (9) identisch ist:

(18b)  Λ(t) = L₀ + M₀ + (2π/J_tr)·(t-t_K), qed.

Anstatt (9) kann (18) als Minuend in Gleichung (1) verwendet werden, denn die ekliptikale Länge der mittleren Sonne S' ist zu jeder Zeit gleich der Rektaszension der mittleren Sonne S''.

Anhang 6: ZG₁+ZG₂, Länge der Jahreszeiten    ↑ zurück

Die Summanden ZG1 und ZG2 in [2] sind als einfache sin-Funktionen Näherungen, während ZG₁(t) und ZG₂(t) (s.Abb.7) mit den genannten Annahmen exakt berechnet sind. Die Summe letzterer ist dennoch nur eine Näherung an die Zeitgleichung (aber besser als in [2]), vor allem weil in ZG ₂(t) die Abhängigkeit der Jahreszeit-Längen von der elliptischen Form der Erdbahn und der Differenz zwischen Perihel und Wintersonnenwende nicht berücksichtigt ist. Alle vier Jahreszeiten sind verschieden lang, was folgende Rechnung zeigt:

Setzt man in Gleichung (7) die α-Werte 0, (π/2), π, (3π/2) und 2π ein und rechnet zurück, so findet man für t-t_k die Werte 78,8; 171,6; 265,2; 355 und 444 Tage (Jahr 2008/09). Das ergibt für die Jahreszeiten folgende Längen:

92,8 Frühlings-,
93,6 Sommer-,
89,8 Herbst- und
89,0 Winter-Tage.

11. Nachtrag 2024

11.1 Jahreskonstanten bzw. Basiswerte

Bei der Beachtung der sich langsam verändernden Einsflüsse auf die Werte der Zeitgleichung wird auf sogenannte Jahreskonstanten bzw. Basiswerte zurückgegriffen. Um welche Größen es sich handelt, ist vor den Rechenbeispielen im Abschnitt 7. dargestellt. Anstatt deren Werte in jedem Jahr erneut aus der Literatur zu beschaffen, kann man sie den sogenannten Bahnelementen, die mindestens wärend eines Menschenalters nicht erneuert werden müssen, entnehmen bzw. sie mit diesen Funktionen der Zeit selbst berechnen.

Die Werte lassen sich grundsätzlich für jeden Tag eines Jahres berechnen. Bei e und ε sind die Änderungen mit der Zeit aber so klein
(Δε = 0,000013°/Jahr und gar Δe = 0,00000042°/Jahr),
dass jeweils ein für ein ganzes Jahr gebrauchter Wert (Jahreskonstante) praktisch genügt.
Bei den Rechenbeispielen ist so vorgegangen worden.
Für den 1. Januar 2014 ergeben die Gleichungen 1. und 2. mit
t gleich 5114 Tagen ab 1.1.2000 die gleichen Werte wie die in den Beispielen verwendeten:
e = 0,016703° und
ε = 23,437346°

Die ekliptikale Länge des Perigums L ( in [11]) ändert sich übers Jahr deutlich, was üblicherweise und auch hier beachtet wird.
Der konstante Term -77,06° in der 3. Gleichung ist der Startwert für t=0. In den Rechenbeispielen wird er als L₀ bezeichnet. Mit t= 5114 Tagen in der 3. Gleichung findet man L = -76,82° bzw. L₀ = -76,82°als Startwert bei Zählbeginn mit t=0 am 1.1.2014.

Mit der 4. Gleichung wird die vorgegebene, unabhängige Variable Zeit t in Winkelwerte für die tägliche Position einer ersten Vergleichsonne auf der Ekliptik bzw. in die Rektaszension α_M (L in [11]) einer zweiten Vergleichssonne auf dem Himmelsäquator umgerechnet. Beide Winkelwerte werden vom Frühlingspunkt aus gerechnet (ihr Wert ist dort jeweils Null).
Im Start-Wert -79,5344° in der 4. Gleichung ist die Jahreskonstante M₀ enthalten, die oben explizit vorkommt (Abschnitt 4.1). Sie ist die Winkeldifferenz zwischen Perigäum und 1. Januar 12:00 der für 365,25 Tage gleichmäßig geteilten Ekliptik und hat bei Zählbeginn am 1.1.2000 den Wert -2,4744° [1].
Der Startwert entsteht durch Vergrößern der Jahreskonstante L₀ mit dieser Differenz (s. Gl. (9) im Abschnitt 6.):
L₀ + M₀ = -2,4744° - 77,06° = -79,5344°.

11.2 Wann welche Zeitgleichung?

Siegfried Wetzel, CH 3400 Burgdorf, Dezember 2007 (Mär.11, Okt.13, Jan.14, Apr.14, Jul.24)

 ↑↑ Anfang
<< andere Sonnenuhren-Beiträge     Druck-Version (Status März 11, 2-spaltig, 6 Seiten, *.pdf, 2.2 mB) >>
<< Home