<< Home Die Physik der Sonnenuhr(Schriften der "Freunde alter Uhren", 1998) Inhalt1. Einleitung 1. Einleitung ↑ AnfangMit der Polstab-Sonnenuhr wird die abschliessende Gnomonische Erfindung bereits am Ende des Mittelalters gemacht. Physik (inklusive Astronomie) und Mathematik sind aber erst in der Neuzeit in der Lage, die Sonnenuhren ausreichend zu erklären. Eigenartigerweise scheint aber jetzt erst (17.Jahrhundert) die einschlägige Erfindertätigkeit richtig zu beginnen. Der Schein trügt. Die Neuzeitlichen Erfindungen müssen häufig als nicht einmal besonders praktische Nebenprodukte mathematischer Uebungen, wofür sich die Gnomonische Sonnenuhr mit ihrem Punkt-Schatten besonders gut eignet, angesehen werden. Von ihnen handelt ein grosser Teil der umfangreichen, auch heute dazu erscheinenden Literatur und versperrt den Blick auf das Grundsätzliche. Dieser Artikel ist ein Versuch, die wenigen physikalischen Erklärungen, die für das Verständnis der eigentlichen Funktion einer Sonnenuhr -nämlich der Zeitanzeige- nötig sind, herauszustellen. Die nicht minder faszinierende mathematisch dominierte Sonnenuhren-Tätigkeit seit der Neuzeit bis heute sollte einmal gesondert zusammenfassend besprochen werden. Zunächst wird das astronomische Grundwissen zum Verständnis einer Sonnenuhr repetiert und in einem Merkzettel festgehalten. Form dieses Merkzettels ist ein Kunstgegenstand, nämlich eine Gartenplastik. Danach wird die Schattenbildung als optische Erscheinung behandelt. Schliesslich wird für die Behandlung der sogenannten Zeitgleichung entsprechendes astronomisches Wissen eingehender besprochen. 2. Sonnenuhren-Grundprinzipien ↑ AnfangAls "Zeiger" auf einer Sonnenuhr dient entweder der Schatten eines Punktes oder der eines Stabes. Sonnenuhren mit Punkt-Schatten wollen wir Gnomonische Sonnenuhren nennen, in Anlehnung an die ersten Sonnenuhren überhaupt, bei denen die Spitze eines senkrechten Stabes -eines Gnomons- als Schattenwerfer diente.
<< Abb.2 Horizontale Sonnenuhr nach dem Polstab-Prinzip (Stolpen/D) In Abb.1 ist eine Gnomonische Sonnenuhr zu sehen. Vorausgesetzt, diese spekulative Rekonstruktion [1] kann bewiesen werden, hatte der Römische Kaiser Augustus die eindrücklichste, weil grösste jemals gebaute Sonnenuhr. Den Punkt-Schatten soll die auf den Obelisken gesetzte Kugel erzeugt haben. Die Sonnenuhren mit Stab-Schatten heisen Polstab-Sonnenuhren, weil der Schatten-werfende Stab in Richtung der beiden Himmels-Pole zeigt. Abb.2 zeigt eine Polstab-Sonnenuhr aus dem letzten Jahrhundert mit horizontalem Zifferblatt. Anstatt eines Stabes ist hier ein stabileres Blech verwendet. Dessen Rand-Schatten dient zur Zeitanzeige. 
<< Abb.3 Gartenplastik "Sonnen-Sektor" (Modell) 3. Astronomisches Grundwissen ↑ AnfangIn Abb.3 ist eine Gartenplastik zu sehen. Ihr Titel heisst "Sonnensektor". Aus der oberen Kugelhälfte ist ein Sektor derart ausgeschnitten, dass die Kugelmitte zu jeder Jahres- und Tageszeit von der Sonne beschienen werden kann. Wenn wir nur die sphärische Oberfläche dieser Plastik betrachten, so können wir jene als Darstellung des Himmels über und unter uns gemäss naiver Vorstellung mit Geozentrischem Weltbild ansehen. Der waagerechte Schnitt teilt wie der Horizont die Himmelssphäre in die obere sichtbare und in die untere nicht sichtbare Hälfte. Der in der Plastik fehlende Teil des sichtbaren Himmels ist dann derjenige, in dem ein irdischer Beobachter (von einer mittleren geographischen Breite aus) am Tage die Sonne sehen und ihre Bewegung wahrnehmen kann. Unsere naive Vorstellung von einer sich bewegenden Sonne stört nicht, da wir in der Plastik nur die relative Bewegung zwischen Erde und Sonne darstellen und alle anderen Himmelskörper ausser acht lassen wollen. 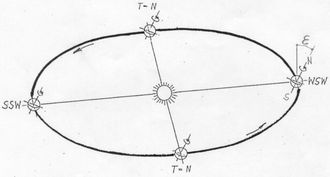 << Abb.4 Heliozentrisches Weltbild Da nun aber die von uns beobachteten Sonnenbahnen in einem irdischen Bezugssystem nicht einfach zu beschreiben und auch noch vom Beobachtungsort (geographische Breite) abhängig sind, wollen wir zunächst umgekehrt die Bewegung der Erde von der Sonne aus betrachten. Das dementsprechende Heliozentrische Weltbild ist in Abb.4 enthalten. Uns interessiert:
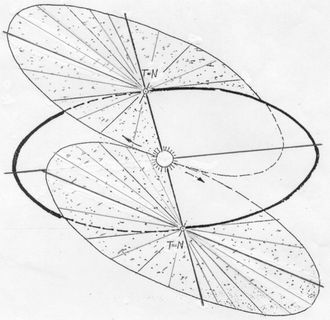 << Abb.5 Scheinbare Sonnen-Bahnen an den T=N - Gleichen Die nächsten drei Abbildungen führen uns wieder zurück zum alten Geozentrischen Weltbild des Ptolemäus und unserem naiven Erleben. In Abb.5 und 6 sind vier besondere Orte der Erdbahn bzw. vier besondere Tage eines Jahres ausgewählt und die jeweilige Kreisbahn (Tagesbahn) der Sonne dargestellt, wie sie von der (durchsichtig angenommenen) Erde aus während des jeweiligen Volltages erscheint. Zwischen Erde und Sonne sind Seh-Strahlen -in umgekehrter Richtung sind es Sonnen-Strahlen- gezeichnet, die an den Wendetagen (Sommer-Sonnen-Wende =SSW und WSW) Kegelmäntel, an den Tag/Nacht-Gleichen (T=N) ebene Kreisflächen bilden. Die Kegel sind an den Wendetagen am spitzesten. Danach werden sie wieder stumpfer, um an den Tag/Nacht-Gleichen in Ebenen auszuarten und dabei ihre Spitzen-Richtung umzukehren. Die Kreisbahnen sind mittels 24 Strahlen gleichmässig unterteilt. Es entspricht der Teilung des Volltages in 24 Stunden. 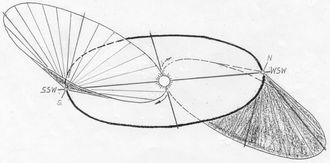 << Abb.6 Scheinbare Sonnenbahnen an den Sonnenwende-Tagen In Abb.7 sind schliesslich die vier verschiedenen Beobachtungen aus den Abbildungen 5 und 6 in einer zusammengefasst dargestellt (zwei Kreisflächen, die in einer zusammenfallen, und zwei Kegelmäntel). Die Flächen sind zusätzlich von einer Himmelssphäre eingehüllt: Sphärenradius gleich Abstand Erde-Sonne. Ihre gemeinsame Achse ist die des Himmels, d.h. die in den Himmel hinaus verlängerte Erdachse. Die Himmels-Sphäre ist schliesslich von einem Horizont der nördlichen geographischen Breite φ halbiert und das Ganze so gedreht, dass unsere Plastik aus Abb.3 unschwer wiederzuerkennen ist.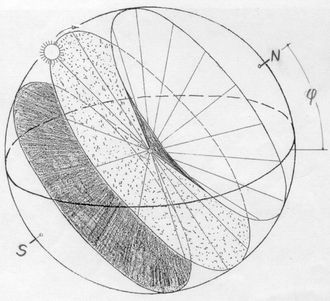 
Abb.7 Scheinbare Sonnenbahnen Die Plastik ist in Abb.8 nochmals gezeigt. Der Achsstummel markiert den nördlichen Himmelspol (Polarstern), eine weitere kleine Kugel symbolisiert die Sonne. In ihr kreuzen sich zwei zusätzliche ebene Scheiben: eine für T=N, die andere für die Mittags-Stunde (deren Stunden-Ebene). Folgende Aussagen werden verständlich:
 << Abb.8 Gartenplastik "Sonnen-Sektor" (Abb.3 mit Ergänzungen) Bei der Teilung der Sphäre mittels eines Horizontes haben wir deren Zentrum stillschweigend auf die Erd-Oberfläche verlegt. Diese Ungenauigkeit stört keineswegs, denn jede irdische Abmessung -selbst der Erdradius- ist gegenüber der Entfernung zur Sonne vernachlässigbar klein. Beachtet werden muss allerdings die geographische Breite. Die Achse der Rotationsflächen im "Sonnensektor" ist nämlich immer eine Parallele zur Erdachse, während der Horizont mit ihr den veränderlichen Breitenwinkel φ einnimmt: Abb.9. Jenseits des Polarkreises würde sich die Kegelmantelfläche WSW gänzlich unter dem Horizont (Polar-Nacht ) und die Fläche SSW gänzlich darüber (Polar-Tag) befinden. Eine Plastik für den Aequator hätte einen aufrechten "Sonnensektor", wobei alle Tagesbögen Halbkreise wären (Tag und Nacht sind ganzjährig gleich lang). 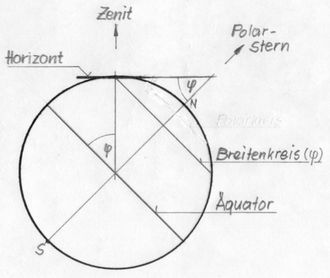 << Abb.9 Meridian-Schnitt der Erde (Schnitt durch die Pole) 4. Schatten und Optik ↑ AnfangJeder Schatten ist eine optische Abbildung, nur im umgekehrt üblichen Sinne: Anstatt eines Licht-Bildes erhalten wir ein Schatten- Bild. 4.1 Schatten-Bild einer Gnomonischen Sonnenuhr ↑ AnfangBei einer Gnomonischen Sonnenuhr ist es dieselbe Abbildung wie im Fotoapparat oder beim Sehen mit dem Auge. Dem Gegenstand angemessener ist, wenn wir uns dem Vorgänger des Fotoapparates -der Lochkamera (als camera obscura lange vor der Fotografie bekannt)- zuwenden. Bei ihr erhält man ein Licht-Bild der Welt, erzeugt von Licht, das durch ein kleines Loch fällt. Bei der Sonnenuhr entsteht ein Schatten-Bild, erzeugt von Nicht-Licht (sprich Schatten), d.h: Licht wird von einem kleinen Nicht-Loch (sprich kleine schattenwerfende Scheibe oder Kugel) ausgeblendet. Wird wie in Abb.16 eine Scheibe mit Loch und dessen Licht-Bild der Sonne als Uhr-"Zeiger" verwendet, so ist diese Sonnenuhr selbst eine Lochkamera. Im Schatten-Bild des Himmels kann man allerdings ausser dem Ort der Sonne nichts erkennen, weil alle anderen Himmelskörper im Vergleich zur Sonne so Licht-schwach sind, dass sie keinen erkennbaren Schatten werfen. Das ist bei einer Sonnenuhr kein Nach- sondern ein Vorteil, weil ja nur der Ort der Sonne erkennbar sein soll. Wegen der Verwandtschaft zur fotografischen Abbildung wird das Verständnis der Gnomonischen Sonnenuhr erleichtert. So wissen wir z.B., dass ein Fotoobjektiv (gleich wie die camera obscura) ein auf dem Kopf stehendes Bild der Wirklichkeit liefert. Abb.10 illustriert die Zusammenhänge. Sie ist aus Abb.7 hergeleitet, enthält aber nur ein kleines Stück von nur einem Kegelmantel (SSW-Tag), denn mehr ist zur Erklärung nicht nötig. 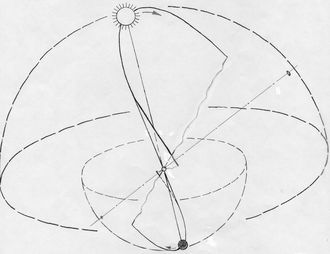 << Abb.10 Punkt-Schatten als Bild der Sonne Anstatt des Beobachters befindet sich die schattenwerfende Kugel in der Kegelspitze, die ebenso die Spitze eines unteren Stückes Kegelmantel ist. Beide Flächenstücke sind in demselben Sinne zueinander umgekehrt, wie der kreisförmige Rand der unteren Fläche das umgekehrte Bild der Sonnenbahn ist: Vormittags-Sonne gleich vorderer (östlicher) Teil des oberen Kreisrandes, Vormittags-Schatten aber gleich hinterer (westlicher) Teil des unteren Kreisrandes, und analog für den Nachmittag. Der obere Kegelmantel enthält diejenigen Sonnenstrahlen, die von der Sonnenuhr-Kugel ausgeblendet werden, die als Schattenlinien einen unteren umgekehrten Kegelmantel bilden. Im Goldenen Zeitalter der Griechischen Antike lebte Berosos, der vermutlich die erste Sonnenuhr baute. Er meisselte in die ebene Oberfläche eines Steines eine halbkugelförmige Vertiefung, in deren Mitte er einen Gnomon aufstellte, dessen Spitze sich in Kugel-Mitte befand. Abb.11 zeigt diese Erfindung, die später Skaphe genannt wurde. Ihre Funktion ist unmittelbar aus Abb.10 erklärbar. Die Schattenbahnen sind -wie die Sonnenbahnen selbst- Kreisbahnen.  << Abb.11 Gnomonische Sonnenuhr des Berosos [2] Es verwundert nicht, dass Berosos seine Sonnenuhr Hemispherium genannt haben soll, ist sie doch auch ein umgekehrtes Modell des sichtbaren Himmels mit einigen Sonnenbahnen. So gesehen hat unsere Plastik "Sonnensektor" (Abb.3+8) ein sehr altes Vorbild. Dass Berosos sich mühte, seinen Stein halbkugelförmig auszumeisseln anstatt ein bequemeres ebenes Zifferblatt zu wählen, könnte auch von seinem Respekt vor dem Himmel bestimmt gewesen sein, den wir dem mächtigen Bauherrn Kaiser Augustus nicht unterstellen brauchten. Andererseits ist die Augustus -Sonnenuhr wegen der Riesenhaftigkeit auch nur mit ebenem "Zifferblatt" vorstellbar (s.Abb.1). Beim ebenen Kegelschnitt entstehen u.a. Hyperbeln, die geradezu Markenzeichen Gnomonischer Sonnenuhren sind. Ein waagerechter Schnitt durch den unteren Kegelmantel in Abb.10 führt zu einer Hyperbel-förmigen Tagesbahn, einer von mehreren, mit denen auf dem Marsfeld in Rom das Jahr unterteilt worden sein soll. 4.2 Schatten-Bild einer Polstab-Sonnenuhr ↑ AnfangDie Schattenbildung mit dem Polstab (s. Sonnenuhr in Abb.2) entspricht ebenfalls einer einfachen -uns aber weniger geläufigen- optischen Abbildung, nämlich der mit einer Zylinderlinse (Abb.12.b). Eine Zylinderlinse ist sogar eine Vereinfachung der im Fotoapparat verwendeten sphärischen Linsen (Abb.12.a).
Das Bild eines Punktes ist bei der zylindrischen Abbildung eine gerade Linie. Ein in der Richtung der Zylinderachse verschobener Punkt führt zum gleichen Linienbild, das mit dem ersten identisch wird, wenn nur die Zylinderlinse genügend lang ist. Der Polstab entspricht der Zylinderlinse. Er erzeugt bei Punkt-Sonnenlicht ein Linien-Schattenbild (Abb.12.c). Gemäss seiner Orientierung parallel zur Erd- und Himmelsachse ist sein Schatten nur mit der Tageszeit verschieden, denn alle Stunden-Ebenen schneiden sich im Polstab. Die jahreszeitlich unterschiedliche Sonnenhöhe führt bei jeder Tageszeit lediglich zu geringer Verschiebung der Schattenlinie auf sich selbst, die bei üblicher Stablänge nicht wahrgenommen wird. Beim Stab-Schatten wird nämlich wie beim Zeiger der Mechanischen Uhr nur die (eindimensionale) Richtung als Zeitangabe verwendet. Die Jahreszeit (zweite Dimension) ist eliminiert. Ein Einzel-Erfinder der Polstab-Sonnenuhr ist nicht bekannt. Sie tauchte nach den Kreuzzügen bei uns auf, so dass anzunehmen ist, dass sie die Kreuzfahrer bei den Arabern im Orient kennenlernten. Eine bessere Sonnenuhr wurde nicht mehr erfunden, obwohl wir das Wissen zum Verstehen der Sonnenuhren erst mit dem Heliozentrischen Weltbild des Kopernikus nach dieser abschliessenden Erfindung erlangten. 5. Ursachen und Korrektur der Zeitgleichung ↑ AnfangWer es mit der Benutzung einer Sonnenuhr genau nimmt, wird feststellen, dass diese auch bei grösster Sorgfalt gegenüber einer Mechanischen Uhr im Laufe eines Jahres zeitweise vor- oder nachgeht. Die Abweichung ist sogar beträchtlich, sie kann ca. eine Viertelstunde betragen. Welche Uhr geht richtig?
 Abb.14 Tägliche Schwankung des Wahren Volltages >> Nun, die heutige Mechanische Uhr geht gleichmässig. Die Sonne dagegen bewegt sich in geringem Masse ungleichmässig schnell am Himmel, was wir aber mit unseren Sinnen nicht wahrnehmen können. Deshalb waren es die Astronomen, die eine Mittlere Sonne erdachten. Diese ist gleichmässig schnell, ihr Ausdruck ist letztlich der gleichmässige Lauf der Mechanischen Uhr. Für die veränderliche Differenz zwischen Mittlerer und Wahrer Sonne wurde der unglückliche Begriff Zeitgleichung geprägt. Wir wollen dem quantitativen Teil dieser Denkarbeit nicht folgen, aber den Ursachen für diesen "Fehler" der Sonnenuhr nachgehen. Dafür müssen wir das im Abschnitt 3 schon besprochene Heliozentrische Weltbild (Abb.4) nochmals, aber genauer ansehen:
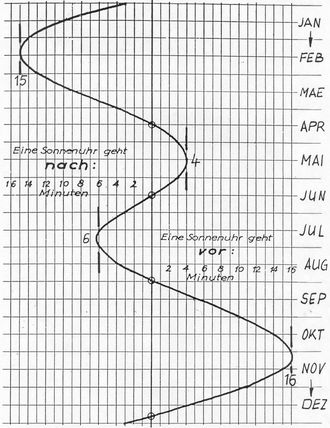
Abb.15 Vor- und Nachgehen
Die beiden periodischen Vorgänge sind in Abb.14 dargestellt. Kurz vor der Herbst- T=N -Gleiche und kurz nach der WSW sind die zusammengesetzten Wirkungen am extremsten. Durch fortlaufende Addition der Tageslängen-Schwankungen um den Mittelwert 24 Stunden entsteht die Zeitgleichung (Abb.15). Sie hat ihre Extremwerte später als die Tageslängen, ihre Haupt-Extreme erst im Oktober/November und im Februar.  << Abb.16 Gnomonische Sonnenuhr an einem Schulhaus (Kloten/CH) Die beiden Neben-Extreme befinden sich im sonnigen Halbjahr, wenn "Saison" für Sonnenuhren ist. Diesen Trost hat der Sonnenuhren-Freund wenigstens. Der Untröstliche braucht aber Abhilfe, die er bei einer Sonnenuhr mit automatischer Korrektur der Zeitgleichung findet. Dafür ist eine Gnomonische Uhr nötig, die die Jahreszeit mit anzeigt. Denn wir erinnern uns: Bei einer Polstab-Uhr ist die Jahreszeit eliminiert. Relativ zur geraden Stundenlinie der Mittleren Sonne hat die der Wahren Sonne die Form einer gestreckten Acht (8). In Abb.16 sehen wir solche für volle Stunden. Wegen der Doppeldeutigkeit muss man das Halbjahr schon kennen: Der S-Teil der 8 gilt bis zur SSW, der ?-Teil der 8 danach bis zur WSW. Für grössere Auflösung müssten weitere 8-Linien aufgenommen werden. Bevor sich diese aber überlagern und die Ablesung gänzlich unübersichtlich würde, weicht man auf wechselbare Zifferblätter aus. Das Zifferblatt in Abb.17 hat nur S-Linien (6 pro Stunde). Bei SSW wird das Blatt mit ?- Linien aufgelegt.  << Abb.17 Korrektur der Zeitgleichung auf wechselbaren Zifferblättern [2] Eine elegantere Korrektur ist in Abb.18 zu sehen. Diese Aequatoriale Sonnenuhr funktioniert für die Korrektur aber nicht wie gewöhnlich als Polstab- sondern als Gnomonische Uhr. Das Zifferblatt ist nämlich auf einen Kreis reduziert und erlaubt somit nur die Ablesung eines Punkt-Schattens. Schattenwerfender Punkt ist ein Ort auf dem Polstab in Kreismitte. Der Polstab ist einmal lang genug, um den zu jeder Jahreszeit nötigen Punkt zu enthalten. Andererseits ist er der Zeitgleichung gemäss verdickt, womit deren Korrektur erfolgt. Die variable Verdickung ist auf der Drehmaschine hergestellt. Für jedes Halbjahr gibt es einen anderen Drehkörper analog zu den vorher erwähnten auswechselbaren Zifferblättern. Bei der abgebildeten Uhr wird bei der Kreuzung des vorrückenden Schattens der vorderen Kante mit der Kreis-Skala abgelesen. Schatten-werfender Punkt ist in diesem Falle ein über den Tag umlaufender Punkt der Stab-Kontur.
6. Literatur (inklusive Bildnachweise) ↑ Anfang[1] E.Buchner "Die Sonnenuhr des Augustus" Mainz, 1982 Siegfried Wetzel, CH 3400 Burgdorf, Januar 2008
↑↑ Anfang |
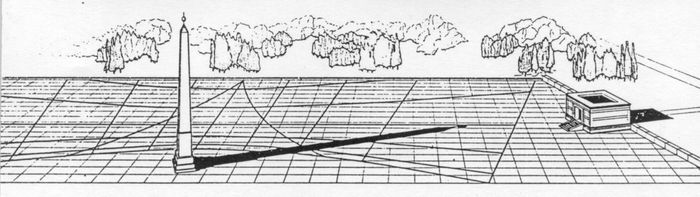Abb.1 Gnomonische Sonnenuhr in Rom (Kaiser Augustus, Rekonstruktion [1])
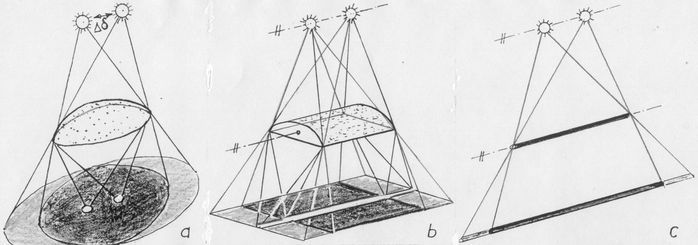Abb.12 Abbildung der Sonne mittels Fotolinse (a), Zlinderlinse (b) und Polstab (c)
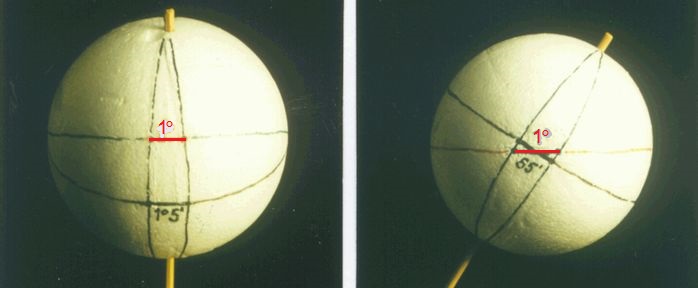Abb.13 Zweite Zeitgleichungs-Ursache; SSW (links), T=N (rechts)
Abb.18 Korrektur der Zeitgleichung mit der Form des Schattengebers (Birkenau/D), montiert ist der Schattengeber für die sonnigere Jahreshälfte.