<< Home
<< andere Sonnenuhren-Beiträge

 ↓↓ Ende

Zum Nachdenken: Verschieben und Verdrehen einer Sonnenuhr

Zusammenfassung

Inhalt

1. Aufgaben-Text, gekürzt  ↑ Anfang

Eine für Wellington (Neuseeland, südliche geographische Breite φ = -41,29°) angefertigte kleine transportable Horizontalsonnenuhr wird zu einem bewohnten Ort in der Steiermark/Österreich, nahe der Grenze zu Niederösterreich gebracht. Dort kann sie genau vertikal so aufgestellt werden, dass sie die Wahre Ortszeit des Nullmeridians anzeigt. Außer dem neuen Aufstellort ist die Abweichung des Zifferblatts von der Südrichtung (Deviation) zu ermitteln.

2. Diskussion der Aufgabenstellung   ↑ Anfang

Auf der als ideale Kugel angenommenen Erde wird es auf einem durch die Steiermark führenden Großkreis viele Orte geben, die für die Lösung in Frage kommen. Eine Einschränkung ist möglich, wenn man statt "nahe der Grenze zu Niederösterreich" liest: "der am nächsten zur Grenze zu Niederösterreich liegende Ort (Dorf oder Stadt)". Der schließlich von mir angegebene Ort bleibt dennoch unsicher, da ich die genauen Koordinaten der bewohnten Orte entlang der steirisch-niederösterreichischen Grenze - vor allem aber die Koordinaten der Grenzsteine - nicht kenne.

3. Umstellen einer horizontalen als vertikale Sonnenuhr
am gleichen Ort  ↑ Anfang

In mittleren geographischen Breiten φ sind sich beide Arten von Sonnenuhren sehr ähnlich. Der Polstab steht in beiden Fällen schräg auf dem Zifferblatt. (Es darf ohne weiteres angenommen werden, das die in die Steiermark gebrachte Uhr einen Polstab hat. Die zu behandelnde Aufgabe ist unabhängig davon, ob die Uhr einen solchen oder einen Nodus als Schattenwerfer hat.) Bei |φ| = 45° ist der Winkel der Schräge gleich, nämlich 45°. Unterschiedlich ist aber in jedem Fall die "Drehung " der Stundenlinien.

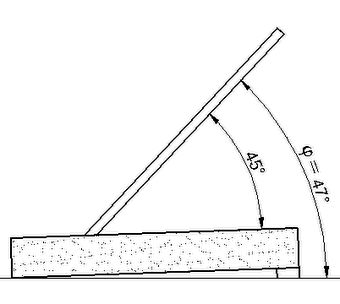
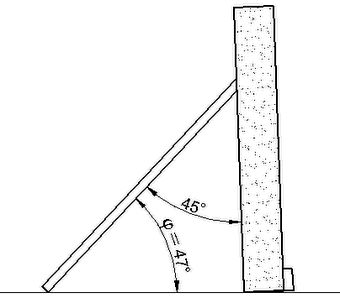
Abb.1 Polstab-Sonnenuhr mit ebenem Zifferblatt für Bern (φ=47°)
links: als horizontale Uhr aufgestellt                                     rechts: als vertikale Uhr aufgestellt

Ein Modell mit 45° schrägen Polstab (Abb.1) machte ich einmal für φ = 47° (Bern) benutzbar. In annähernd horizontaler Aufstellung ist das Zifferblatt an der nördlichen Kante 2° angehoben. In annähernd vertikaler Lage kippt es 2° vornüber. Dem "fauleren" und auffälligeren Kompromiss bei der Drehrichtung der Stundenlinien bin ich begegnet, indem ich das Zifferblatt spärlich beschriftete.

4. Aufstellung einer horizontalen als vertikale Sonnenuhr auf der anderen Seite des Erdäquators  ↑ Anfang

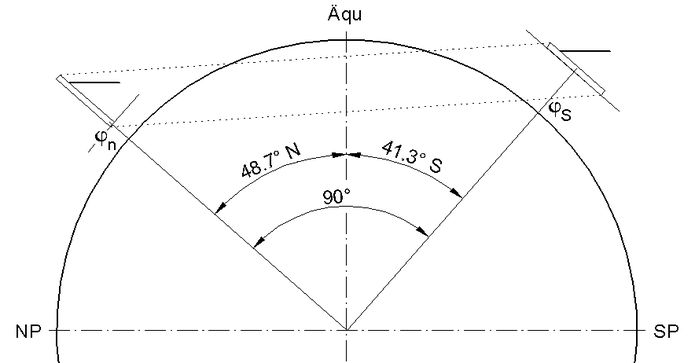Abb.2 Verschiebung einer horizontalen Sonnenuhr mit ebenem Zifferblatt von φ_S=-41,3° (Neuseeland) zu φ_n=+48,7° (Österreich)

Österreich liegt von Neuseeland (Wellington: φ_S = -41,29°) aus gesehen auf der anderen Seite des Äquators. Die in die Steiermark gebrachte horizontale Sonnenuhr kann allerdings dort nicht gemäss Abb.2 als Vertikaluhr verwendet werden, denn sie müsste auf
φ_n = φ_S + 90° = -41,29° + 90° = +48,71° (Abb.2)
stehen. Dieser Breitengrad φ_n befindet sich weiter im Norden, er quert die Bundesländer Ober- und Niederösterreich Analog zu meinem in Abb.1 gezeigten Vorgehen müsste die Uhr an seinem steirischen Bestimmungsort lediglich ein wenig nach Süden gekippt aufgestellt werden, und das Nachdenken wäre beendet.

Das ist natürlich nicht im Sinne des Aufgaben-Erfinders. Also ist ein nicht-üblicher Gebrauch für das importierte Stück vorgesehen, bei dem zufällig (!) die exakt senkrechte Aufstellung möglich wird: Anzeige der Wahren Zeit des Nullmeridians (WNZ) anstatt der Wahren Zeit des Aufstellortes (WOZ). Dass jemand Interesse an dieser eigenartigen Anzeige hat, wird stillschweigend unterstellt.

5. Drehen einer Sonnenuhr um ihren Polstab  ↑ Anfang

Das Ergebnis dieser besonderen Aufstellung ist vergleichbar mit dem Zurückstellen einer Sonnenuhr um zum Beispiel eine Stunde, falls der neue Aufstellort auf dem 15. östlichen Längengrad (λ = -15°) liegt. Es ist bekannt, dass man an einer Sonnenuhr beim Umstellen zwischen Normal- und Sommerzeit nicht wie bei mechanischen Uhren den Zeiger verdrehen kann. Man müsste das Zifferblatt um den Polstab drehen. Da aber in der Regel dieser Stab nicht das Zifferblatt, sondern das Zifferblatt den Stab trägt, muss das Umstellen unterbleiben. Man behilft sich bekannterweise mit einer zweiten Reihe von Stundenziffern. Die vorliegende Aufgabe verlangt aber ausdrücklich das Verdrehen der Zifferblattebene, ungeachtet etwaiger ungünstiger Nebenwirkungen.

5.1 Das Verdrehen

<< Abb.3 zur Berechnung benutzte sphärische Dreiecke

Durch das Verdrehen ändert sich die Orientierung des Zifferblattes. Auf der Breite φ_n war sie vertikal und nach Süden gerichtet, jetzt ist sie leicht nach vorn gekippt und deutlich gegen westwärts verdreht (westabweichend). Damit es wieder genau vertikal steht, muss man die Sonnenuhr weiter südlich aufstellen. Diese südlichere Breite φ_N ist nun auszurechnen (Index N für definitiven Standort auf der Nord-Halbkugel). Dass sie durch den Norden der Steiermark verläuft, wird nicht überraschen, denn dafür ist die gestellte Aufgabe angelegt.

Die nötigen Berechnungen werden mit Hilfe von sphärischen Dreiecken vorgenommen. Deren Seiten sind Großkreis- Schnitte der Stundenebenen der Sonne, der Zifferblattebene und einer horizontalen Hilfsebene mit einer Sphäre, deren Mittelpunkt sich im Fußpunkt des Polstabs befindet (Abb.3)

5.2 Berechnung der geographischen Breite für verdrehtes, vertikal aufzustellendes Zifferblatt

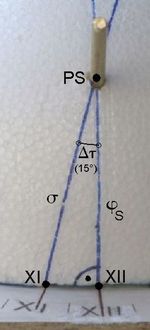<< Abb.4 Sphärisches Dreieck zur Berechnung der geographischen Breite für verdrehtes, vertikal aufzustellendes Zifferblatt

σ ist eine Seite (Bogen) eines sphärischen Dreiecks (Abb.4), dessen Ecken die Durchstoßpunkte des Polstabs (PS) und der Stundenlinien XI und XII auf der Sphäre sind. Eine zweite Dreieckseite ist der Erhebungswinkel des Polstabs über dem Zifferblatt: φ_S . Der Eckwinkel am Durchstoßpunkt PS zwischen diesen beiden Seiten ist Δτ. Am Durchstoßpunkt XII ist der Eckwinkel 90° (hier schneiden sich das Zifferblatt und die Stundenebene XII der Sonne rechtwinklig). Eine der bekannten Hauptbbeziehungen im rechtwinkligen sphärischen Dreieck gibt den gesuchten Winkel σ an:
tanσ = tanφ_S / cosΔτ .   Mit φ_S=41,29° und Δτ=15° ist   φ_N = 47,72° .
Wildalpen/Steiermark mit den Koordinaten 14,98° Ost / 47,65° Nord |* liegt etwa 8 km daneben, um die gesuchte Ortschaft zu sein. Ob lediglich ein bewohntes Haus mit den Koordinaten 15° Ost / 47,72° Nord gemeint ist und ob ein solches existiert, muss offen bleiben. Generell ist die geographische Länge variabel. Der zunächst angenommene Wert λ=-15° diente der Bequemlichkeit: Substilare war dabei nicht irgend eine Stundenlinie sondern die XI-Stundenlinie, also die einer ganzen Stunde.

Die folgende Tabelle enthält ausgerechnete Koordinatenpaare mit variablem λ quer durch die Steiermark:

Δτ=λ /° | -14,875 -15,000 -15,125 -15,250 -15,375 -15,500 -15,625 -15,750
----------------------------------------------------------------------------
  φN /° |   47,74   47,72   47,71   47,69   47,67   47,66   47,64   47,62 
----------------------------------------------------------------------------
  θ /°  |   11,12   11,21                                   11,68   11,77 

• Das Gebiet westlich des ersten Paars scheint bis bis zum westlichen Ende der Grenze zwischen der Steiermark und Niederösterreich unbesiedelt zu sein.
• Das erste Paar passt ganz gut zur Ortschaft Mendling/Steiermark (14,87° Ost / 47,73° Nord) |*, die somit der zu findende Ort sein könnte.
• Die Paare drei bis sechs kommen wegen der nördlichen Ausbuchtung der Grenze (Mariazell) nicht in Frage.
• In der Nähe des vorletzten Paares liegt Mürzzuschlag (15,68° Ost / 47,60° Nord) *|, der einzige größere der möglichen Orte, der aber weniger gut als Mendling passt.
• Das letzte Paar passt besser, nämlich ganz gut zu Spital am Semmering (15,75° Ost / 47,60° Nord) und wäre nach Mendling die zweitbeste Lösung.
• Der nahe Semmering-Pass (15,82° Ost) *| ist schon die östliche der Grenze zu Niederösterreich.

Die angegebene Spur quer durch die Steiermark ist Teil eines Großkreises auf der Erdoberfläche. Seine Mittensenkrechte tritt auf dem Nullmeridian bei φ_S aus der Erde aus, und sein nördlichster Punkt befindet sich auch auf dem Nullmeridian, nämlich bei φ_n (Argentan/Frankreich).

5.3 Berechnung der Westabweichung (Deviation) für verdrehtes, vertikal aufzustellendes Zifferblatt

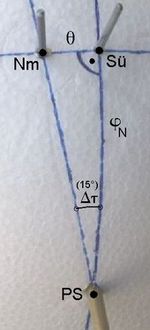<< Abb.5 sphärisches Dreieck zwischen Polstab (PS), Südpfeil (Sü) und Zifferblatt-Normale (Nm)

Die Westabweichung ist der Winkel θ zwischen der Normalen des Zifferblatts und der Südrichtung. Im sphärischen Dreieck, dessen Ecken die Polstabspitze (PS) und die Durchstoßpunkte der in Sphärenmitte (Fußpunkt des Polstabs) aufgesetzen Zifferblattnormale (Nm) und eines dort ebenfalls beginnenden Südpfeiles (Sü) sind, ist er die kurze Seite (Bogen, Abb.5). Eine der langen Seiten ist der Winkel zwischen dem Polstab und der Zifferblattnormale: 90°-β=φ_N. Mit der kurzen Seite bildet sie einen rechten Winkel (Polstab und Normale befinden sich in einer senkrechten, Normale und Südpfeil in einer horizontalen Ebene). Der Eckwinkel bei der Polstabspitze ist wieder Δτ= Δλ. Eine der bekannten Hauptbeziehungen im rechtwinkligen sphärischen Dreieck lautet jetzt:
tanθ = sinφ_N tanΔτ .

In obiger Tabelle sind einige ausgerechnete Werte für θ unter den zugehörenden Koordinatenpaaren eingetragen.

Im Übrigen ist es nicht damit getan, die neue Aufstellung zu berechnen. Diese muss auch praktisch durchgeführt werden. Falls das originale Zifferbatt rechtwinklig begrenzt ist, kann man z.B. einen Keil unterlegen (Abb.6). Dessen Winkel ist der Substilarwinkel α nach bekannter Gleichung (s.a. Abb.3, unten): tan α = sinφ_S tanΔτ .

<< Abb.6 im Gegenuhrzeigersinn um den Polstab verdrehte Sonnenuhr,
mit Keilunterlage aufgestellt, vertikal, aber westabweichend

Man kann die Deviation θ auch wie folgt bestimmen
(Beispiel für λ=-15° / φ= 47,72°):

Zur Tag-Nacht-Gleiche erhält das Zifferblatt Streiflicht bei
VII Uhr WOZ (VI Uhr WNZ, τ=-75°). Der Azimutwinkel a der Sonne gibt die Richtung an, in die die rechte Seite der Zifferblattebene fluchtet. Die bekannte Gleichung lautet:
tan a = sin τ / (sin φ_N cos τ) .
Ergebnis für Beispiel: a = 78,79°.
Das Zifferblatt ist θ = 90° - a = 11,21° westabweichend
(vgl. Tabelle, 2. Spalte).

Siegfried Wetzel, CH 3400 Burgdorf, Januar 2012

 ↑↑ Anfang

<< Home
<< andere Sonnenuhren-Beiträge