<< Home
<< andere Sonnenuhren-Beiträge

 ↓↓ Ende

Zwei Sonnenuhren von Johannes Gaupp

Zusammenfassung

Inhalt

1. Die universale Horizontalsonnenuhr  ↑ Anfang

Gaupp stellte unter dieser Bezeichnung eine Sonnenuhr vor, von der vor ihm Jaques Ozanam bereits mehrere Varianten zeigte und das zugrunde liegende Prinzip angab [2]. Es handelt sich um horizontale Sonnenuhren mit einem im Fußpunkt um die Ost-West-Achse drehbaren Polstab (bei Gaupp ein Flächenstück mit gerader "Polkante"). Der Polstab wird so gedreht, bis er parallel zur Erdachse ist. Das Zifferblatt enthält außer den i.d.R. nicht geraden sogenannten Stundenlinien diese kreuzende, mit der geografischen Breite codierte Linien. Die Zeitanzeige ist ein Punkt in diesem Liniennetz, dem ein bildgebender Punkt (Nodus) auf dem Polstab entspricht. Eine solche Sonnenuhr ist keine Polstab-Sonnenuhr sondern eine mit Nodus. Der bildgebende Punkt ist ein im allgemeinen sowohl über den Tag als auch übers Jahr wechselnder Punkt auf dem Polstab [3]. Von den unendlich vielen möglichen Zifferblatt-Netzen stellte Ozanam nur wenige, und nur solche vor, bei denen die eine der beiden Linienscharen aus Kegelschnitt-Kurven und die andere aus Geraden besteht [4].

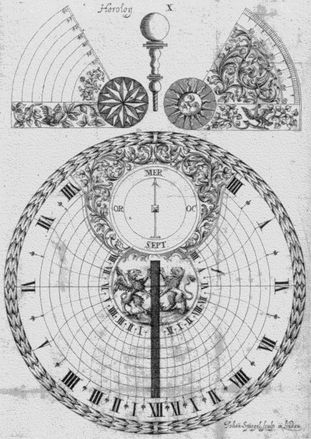Abb.1 Universale Horizontalsonnenuhr von Gaupp, [1]                               Abb.2 Zifferblatt und Schattenwerfer (oben)

Bei der universalen Horizontalsonnenuhr von Gaupp werden als Breitengrad-Linien um den Fußpunkt der Polkante konzentrische Kreise, deren Radius etwa proportional mit dem Breitengrad größer wird, verwendet. Die die Kreise kreuzenden Stundenlinien sind gekrümmt. Mein Eindruck war, dass sie nicht richtig sind, denn die Krümmung muss nach meiner Erfahrung entgegengesetzt sein, was die im folgenden geschildert Nachprüfung bestätigte.

Bei einer Polstabsonnenuhr ist der Skalen-Stundenwinkel in unseren Breiten z.B. für XI / I Uhr etwa ±11° (11,6° bei 50° Breite). Er ist null am Äquator (horizontale gleich polare Sonnenuhr) und 15° an den Polen (horizontale gleich äquatoriale Sonnenuhr). Der Wert wächst stetig mit der Breite, also müssen die Stundenlinien von der XII-Uhr-Linie aus gesehen konvex sein. Gaupp zeichnete konkave Linien. Diese Schnellprüfung wird unterstützt durch Vergleich mit einer Sonnenuhr von Ozanam: einstellbare parabolische Horizontaluhr (Abb.3).

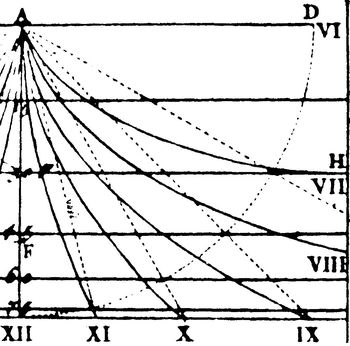
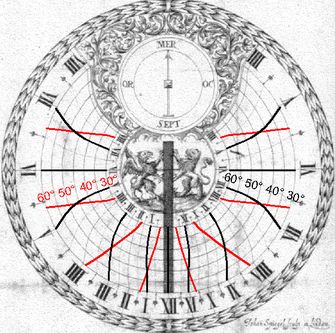Abb.3 Parabolische universale Horizontaluhr von Ozanam,     Abb.4 Uhr von Gaupp, φ-Werte falsch (lks), korrigiert (re)
Vormittags-Hälfte, [2]

In Abb.4 sind über das Zifferblatt von Gaupp für jede zweite volle Stunde die korrigierten Linien in rot eingezeichnet. Die bekannte Gleichung für die Berechnung des Skalen-Stundenwinkels α als Funktion des Stundenwinkels τ und des Breitenwinkels φ ist die folgende:

tan α = tan τ · sin φ .

Nach getaner Arbeit sah ich den wahrscheinlichen Fehler plötzlich deutlich: Gaupp beschriftete offenbar lediglich die mit dem Breitengrad codierten Kreise in falscher Reihenfolge: Er hätte dem größten von ihnen φ= 30° und dem kleinsten φ=60° zuordnen müssen. Kontrolle: Die Paare aus einer schwarzen und einer roten Stundenlinie sind bezüglich einer radialen Linie spiegelbildlich. Ihr jeweiliger Schnittpunkt liegt auf dem 45°-Kreis (in Abb.4 nur annähernd, was u.a. daraus folgen kann, dass das Zifferblatt im Katalog verzerrt wiedergegeben ist).

2. Die universale Horizontal- und Vertikalsonnenuhr   ↑ Anfang

Diese Sonnenuhr (Abb.5) hatte vor Gaupp schon Anasthasius Kircher vorgestellt. Hier wird auch - wie bei der oben beschriebenen Uhr vom Typ Ozanam - ein durch Drehen auf die geographische Breite einstellbares Flächenstück mit gerader Kante als Schattenwerfer verwendet. Die Drehachse schneidet aber die Kante nicht, sondern liegt abseits (Abb.7/links, Abb.9 und Abb.10). Die Zeit-Skala ist lediglich eine Gerade (Abb.7/Mitte und Abb.8). Sie enthält die Drehachse des Schattenwerfers und ist in Ost-West-Richtung zu positionieren. Die "Polkante" des Schattenwerfers muss parallel zur Erdachse sein. Die am Schattenwerfer angebrachte Einstellskala bezieht Gaupp auf die horizontale Lage der Platte, in der sich die Skalengerade befindet. Die Platte enthält kein ebenes Zifferblatt, ist also keine typische Horizontal-Sonnenuhr. Ebensowenig liegt eine typische Vertikal-Sonnenuhr mit ebenem Zifferblatt vor, wenn die Platte vertikal steht und mit dem Komplement des Breitenwinkels zu 90° einzustellen ist (Abb.6).

Abb.5 Univ. Horizontal- u. Vertikalsonnenuhr v. Gaupp, [1]      Abb.6 vertikale Lage
horizontale Lage

Abb.7 Zifferblatt (Mitte) und Schattenwerfer (links und rechts)

In Abb.8 ist die Verwandtschaft dieser Gaupp'schen Sonnenuhr mit einer äquatorialen Ringsonnenuhr erkennbar. Eine solche hat auch einen Polstab als Schattenwerfer, ist aber ebenfalls eine Nodussonnenuhr. Ihr Nodus wandert übers Jahr auf dem Polstab - der der Gaupp'schen Uhr auf der Schattenwerferkante - hin und her. Bei der Gaupp'schen Sonnenuhr ist der Skalenring der Ringsonnenuhr durch eine Tangente an die Mittagsmarke (XII Uhr) ersetzt. Diese gerade Skala hat ihre Stundenmarken dort, wo sie von den verlängerten Stundenlinien, die in der Ringebene liegen, getroffen wird. Der Polstabschatten fällt auf die Skala erst nach VI Uhr morgens und nur bis vor VI Uhr abends. Gaupp hat seine Skala von VII Uhr morgens bis V Uhr abends eingerichtet.

Seine Sonnenuhr, beziehungsweise die Skalengerade seiner Uhr ist für jede geographische Breite nutzbar, weil bei der entsprechenden Einstellung die vom Skalenpunkt XII Uhr auf die Schattenwerferkante gefällte Normale unverändert lang bleibt. Der Radius des zur Erklärung benutzten Skalenrings bleibt konstant und die von ihm abgeleitete Skalengerade unverändert. Durch die Einstellung auf den Breitengrad wird dieser Ring beziehungsweise die Normale äquatorparrallel gemacht.

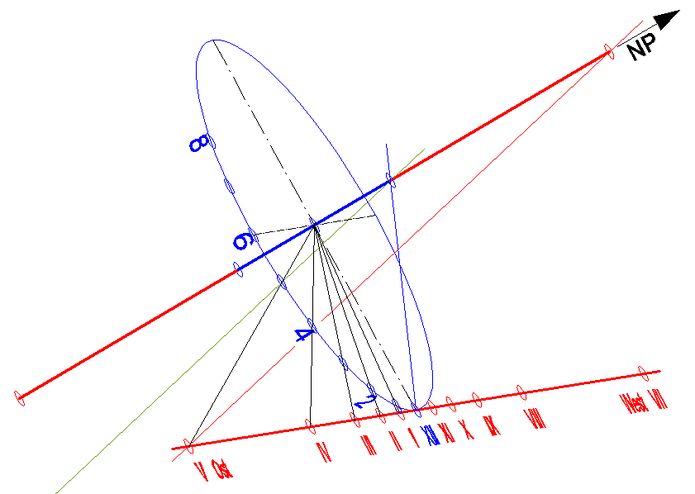Abb.8 Herleitung aus einer äquatorialen Ringsonnenuhr; Nachmittagsstunden zur Sommersonnenwende

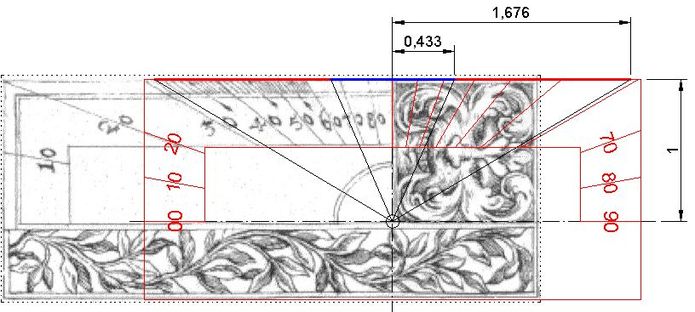Abb.9 Schattenwerfer (Änderungen in rot))

Die Verhältnisse sind im Winterhalbjahr spiegelbildlich bezüglich des ursprünglichen äquatorialen Skalenrings. Das erfordert ein vollkommen symmetrisches Flächenstück mit "Polkante" (Abb.9). Gaupp gestaltete dieses auf der für den Sommer vorgesehenen Seite deutlich zu kurz.

Im Katalog [1] ist nicht darauf hingewiesen, dass in vertikaler Lage (Abb.6) die Einstellung mit dem zu 90° komplementären Breitenwinkel φ (also mit 90°-φ) zu erfolgen hat. Diese Rechenarbeit wird unnötig, wenn man eine zweite Einstellskala anbringt (rechts in Abb.9). Dadurch wird die zweite Skalierung der Zeitgerade hinfällig. Die Uhr wird im Vergleich zu Abb.6 umgekehrt aufgestellt (Abb.10, Kompass unten).

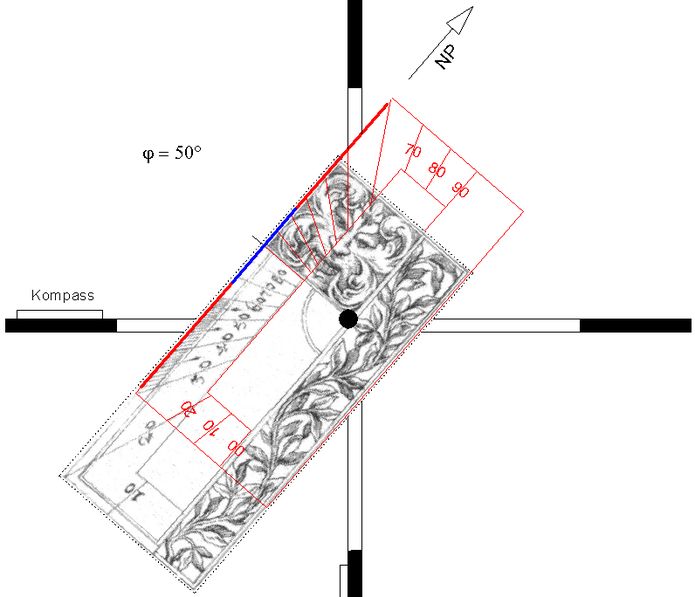Abb.10 geänderter Schattenwerfer in Platte, die beliebig positionierbar ist; Bedingung ist nur,
dass die "Polkante" zum Himmelspol (NP) zeigt (einstellbar mit Winkelskala z.B. gegenüber horiz. o. vert.Platte)

Auf den ersten Blick sieht auch die Sonnenuhr vom Typ Gaupp/Kircher wie eine Polstabsonnenuhr aus, die bekanntlich in horizontaler Ausführung die gesamte Zeit zwischen Sonnenauf- und -untergang anzeigt. Bei einer Nodussonnenuhr (Nodus fix) ist der Anzeigebereich immer verkürzt. Das ist auch bei der vorliegenden Uhr der Fall. Die Erklärungen beider Fälle sind aber nicht gleich:
Nodussonnenuhr: Der Schatten des Nodus fällt gegen Sonnenauf- und -untergang immer weiter und schließlich ins Unendliche.
Horizontale Sonnenuhr Gaupp/Kircher: Der Nodus wandert gegen Sonnenauf- und -untergang wohl zum Fußpunkt der "Polkante", aber sein von dort ausgehender Schatten trifft i.d.R. das nur "linienförmige Zifferblatt" (Skalengerade) nicht (Ausnahme: in kurzen Wintertagen auf genügend hohen geografischen Breiten).

3. Literatur   ↑ Anfang

Siegfried Wetzel, CH 3400 Burgdorf, Oktober 2011 (Mai 13)

 ↑↑ Anfang

<< Home
<< andere Sonnenuhren-Beiträge