<< Home
<< andere Sonnenuhren-Beiträge
 ↓↓ Ende

Breiten-unabhängige Sonnenuhren

(DGC-Mitteilungen Nr.112, 2007)

Inhalt

1. Einleitung
2. Die Schlüssel-Relation
3. Eine "greifbare" y'-Koordinate
4. Gebrauch einer Breiten-unabhängigen Sonnenuhr
5. Eine Breiten-unabhängige Sonnenuhr als Stab
6. Vorteil der Sonnenuhr von Freeman
7. Künftige Breiten-unabhängige Sonnenuhren ?
8. Literatur
9. Anmerkung

1. Einleitung  ↑ Anfang

"Eine Breiten-unabhängige Sonnenuhr" war der Titel einer Arbeit von Freeman [1], in der eine solche Uhr erstmals beschrieben wurde. Das "Sonnenuhren Handbuch" der DGC [2] enthält das Kapitel "Breitenunabhängige Sonnenuhren", in dem diese Uhr aufgenommen und unter Bezug auf die Relation

(1)   sin τ · cos δ  =  sin a · cos h

auf eine Einfachst-Ausführung abstrahiert wurde. Diese Ausführung ist wie die von Freeman eine ebene Sonnenuhr.

Die genannte Relation drückt die Tatsache aus, dass die y- (Ost/West-) Koordinate der Sonnenposition sowohl im System des Ortsäquators als auch des Horizonts von der Breite unabhängig ist. Somit lässt sich dieser Sonnenuhren-Typ auf eine in Ost/West-Richtung positionierte Gerade (Stab) reduzieren. Eine solche Minimal-Sonnenuhr wurde gebaut und wird hier vorgestellt.

Im Vergleich zur Einfachst-Ausführung [2] wird die Erfindungshöhe (ein aus dem Patent-Wesen stammender Begriff) der Sonnenuhr von Freeman angegeben. Die Ausführung [2] wurde ebenfalls gebaut.

Zum Schluss wird der Frage nachgegangen, inwiefern die genannte Relation der Schlüssel zu bisher nicht bekannten Breiten-unabhängigen Sonnenuhren sein kann.

2. Die Schlüssel-Relation    ↑ Anfang

Die oben genannte, hier als Schlüssel-Relation bezeichnete Formel lautet ausführlicher

(2)   y' = sin τ · cos δ     ≡    sin a · cos h = y .

Gleich sind nämlich die y-Koordinaten der gebräuchlichen Koordinaten-Systeme (y' im Ortsäquator-, y im Horizont-System). Sie liegen beide in Ost/West-Richtung. Die Systeme gehen durch Drehung (90°-φ) um die Ost/West-Achse auseinander hervor. Somit ist die y-Koordinate des einen Systems mit der des anderen identisch (y'=y) und ist keine Funktion der geographischen Breite φ. Wenn also stellvertretend für das Produkt sin τ · cos δ das Produkt sin a · cos h gebraucht wird, so kann auf den Stundenwinkel τ durch Ermittlung des Azimuts a und des Höhenwinkels h bezüglich eines beliebigen Horizontes (bei bekannter Deklination δ) geschlossen werden.

In den Darstellungen [1] und [2] wird ein ebenes Zifferblatt auf dem Orts-Horizont zur Anzeige des Stundenwinkels gebraucht und zur Erklärung auf Azimut und Höhenwinkel eingegangen. Letztere führen unter Beachtung der Deklination (d-Einstellung) zu einer Länge auf einer Ost/West-Geraden als Mass für den Stundenwinkel, ohne dass sie explizit gemessen werden. Das legt folgende Schlussfolgerung nahe:

• Anstatt eines Ziffern-Blatts genügt eine Ziffern-Gerade, nämlich eine mit t skalierte Linie.
• Anstatt eines Grundbretts genügt ein in Ost/West-Richtung positionierter Stab, der die t-Skala trägt.
• Auf Azimut und Höhenwinkel kann bei der Erklärung der Wirkungsweise verzichtet werden zu Gunsten des Augenmerks auf die y'-Koordinate als Funktion des Stundenwinkels (und der Deklination ! ).
• Als Schlüssel-Relation braucht nur y' = sin τ · cos δ angesehen werden.

3. Eine "greifbare" y'-Koordinate  ↑ Anfang

Die Orts-Beschreibung von Himmelskörpern ist wegen deren "nicht greifbarer" Entfernung nur mit Winkel-Angaben möglich (und üblich). Man setzt alle Körper auf ein- und dieselbe Himmels-Sphäre und macht deren Radius hilfsweise zu 1 (Einheits-Radius). Einer karthesischen Koordinate wie y' = sin τ · cos δ liegt dieser zu Grunde. Der Ursprung der Koordinaten-Systeme ist immer Mittelpunkt einer Richtungs-Kugel mit Radius 1 (eins).

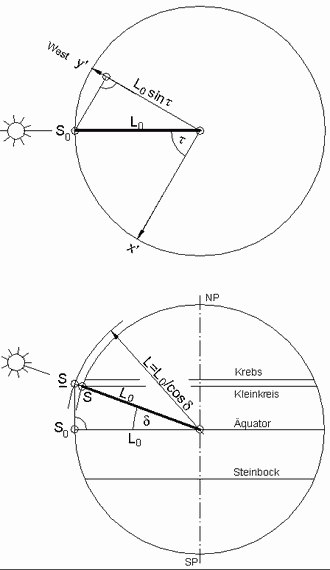
<< Abb.1 Sonne (Subsolarer Punkt) im Koordinaten-System des Ortsäquators

Zu einer "greifbaren" y'-Koordinate gehört die Vorstellung einer entsprechend kleinen Einheits-Kugel (Abb.1). Die zu messende Sonne wird auf ihr durch den Subsolaren Punkt S vertreten. Der "reale" Einheits-Radius sei L₀.

Im Sonderfall δ=0 (Abb.1, oben, Äquator-Ebene) befindet sich die Sonne bei S₀ in der Äquator-Ebene, in der der Stundenwinkel definiert ist. Die Projektion des Ortsvektors der Sonne auf die Ost/West-Achse ist deren y'-Koordinate:

(3)   y' = L₀ · sin τ    >>    sin τ = y' / L₀ .

Im allgemeinen Fall δ ≠ 0 (Abb.1, unten, Stundenebene) befindet sich die Sonne auf einem Kleinkreis bei S. Verschiebt man die Sonne zu S (grössere Kugel, Radius L=L₀/cos δ), so ist die Projektion ihres Ortsvektors in die Äquator-Ebene L₀, und die Projektion auf die y'-Koordinate hat denselben Wert wie bei δ=0:

(4)   y' = (L₀/cos δ) · sin τ .

Die Sonnen-Deklination ist im allgemeinen Fall berücksichtigt, wenn ein Stück Sonnenstrahl der variablen Länge L=L₀/cosδ betrachtet wird.

(5)   y' = L · sin τ    >>    sin τ = y' / L .

Die Schlüssel-Relation (s.2.) lautet in Worten:
Der vektorielle Anteil eines Stücks Sonnenstrahl der Länge L=L₀/cos δ beträgt in Ost/West-Richtung y'=L·sint. Seine Messung ist eine indirekte Messung des Stundenwinkels, worauf die geographische Breite des Mess-Ortes keinen Einfluss hat (wohl aber die Deklination ! ).

4. Gebrauch einer Breiten-unabhängigen Sonnenuhr  ↑ Anfang

Die Einfachst-Version [2] ist wie folgt zu gebrauchen:

• Länge L=L₀/cosδ an Peilstab einstellen
• L mit Sonnenstrahl zur Deckung bringen (Peilen)
• L auf Ost/West-Achse projizieren (Tasten)

Angesichts dieses Aufwands kam Freeman bei der Vorstellung seiner Sonnenuhr selbst zum Schluss, dass es sich "eher um eine wissenschaftliche Kuriosität als um ein Instrument für den praktischen Gebrauch" handle. Dabei ist seine Version etwas einfacher als oben zu gebrauchen (s.6.). Die Kuriosität besteht darin, dass man weder bei Bau, Aufstellung noch Gebrauch die geographische Breite beachten muss. Der unpraktische Gebrauch kommt daher, dass diese Sonnenuhr passiv ist. Mehrfach aktiv hat der Benutzer zu sein, bevor sich τ als Winkel oder Tagesstunde ablesen lässt.

Die bereits von Freeman stammende Bezeichnung "Breiten-unabhängige Sonnenuhr" macht somit jedem Waren-Prospekt Ehre, der mehrere Nachteile des Produkts zu Gunsten eines einzigen Vorteils verschweigt. Von einer Sonnen-Uhr wird nämlich vor allem erwartet, dass sie die Tageszeit ohne Zutun des Benutzers anzeigt. Das vorliegende Produkt braucht mehr Benutzer-Aktivität als der ebenfalls passive Zollstock "in der Hand" eines Heimwerkers. Es gibt noch andere passive Sonnenuhren, z.B. die Analemmatische Sonnenuhr, die allerdings einfacher zu gebrauchen und "unter den Füssen" vieler Benutzer recht beliebt ist.

Bei bestimmten Stundenwinkeln ist die Messung zudem ungenau und zweideutig:

• Die Messung wird bei τ = 90° ± Δτ wegen des dort gering ändernden Wertes ziemlich ungenau.
• Weil sin ( 90° + Δτ ) = sin ( 90° - Δτ ), ist nicht zu erkennen, ob t>90° oder t<90° gilt.

5. Eine Breiten-unabhängige Sonnenuhr als Stab  ↑ Anfang

Trotz obigem, grundsätzlich ungünstigem Urteil sei eine infolge näherer Betrachtung der Schlüssel-Relation (s.2.) entstandene Stab-Sonnenuhr vorgestellt (Abb.2). Das bisher übliche Grundbrett ist zu Gunsten eines Ost/West-Stabes aufgegeben, was den Umfang reduziert (Minimal-Version) und zudem das Mess-Prinzip besser erkennen lässt.

<< Abb.2 Breiten-unabhängige Sonnenuhr als Stab
oben: Sonnenuhr ; unten: Messvorgang

An einem inneren Schiebe-Stabes ist ein in seiner Länge einstellbarer Peilstab gelenkig befestigt. Zur Längeneinstellung dient eine δ-Skala (tanδ), die sich auf der mit äusseren Rohr fest verbundenen Tast-Scheibe befindet und aus Ringen besteht. Rohr und Schiebestab sind in Ost/West-Richtung zu positionieren. Der Peilstab wird gegen die Sonne gerichtet. Bei erreichter Peilung fallen der Schatten eines kleinen Querstabes bei der Spitze und der der verlängerten Achse des Gelenkes (Abb.2, unten) zusammen. Die Tast-Scheibe lässt die Sonne durchscheinen. Der Schiebestab wird verschoben bis die Spitze des Peilstabes die Scheibe berührt. Auf der τ-Skala (sinτ) des Schiebestabes ist die Tageszeit ersichtlich.

Die Uhr ist für den halben Tag ausgeführt. Für die Anzeige von Vor- zu Nachmittags-Stunden (Skala doppelt beschriftet) ist von Ost- auf West- Orientierung umzustellen. Die Tastscheibe ist als Vollkreis -also übertrieben gross- ausgeführt, um auf die Unabhängigkeit von φ hinzuweisen. Der Vollkreis symbolisiert den ganzen Meridian, kein Horizont ist ausgezeichnet.

6. Vorteil der Sonnenuhr von Freeman
↑ Anfang

Freeman's Version setzt ein Zifferblatt, also das horizontale Grundbrett voraus. Um die enthaltene Erfindungshöhe zu würdigen, wird die Uhr mit der Einfachst-Version [2] verglichen (Abb.3). Freeman's Erfindung im engeren Sinne ist Folgendes:

• Die verwendete Vorrichtung braucht nur azimutal eingestellt zu werden (vereinfachtes Peilen, s.a. Anmerkung).
• Die y'-Koordinate des Sonnenstrahls L₀ wird direkt angezeigt (kein Tasten).

In der Version [2] muss auch in Höhe gepeilt und die Projektion des im Raum eingestellten Stabes der Länge L händig vorgenommen werden (Tasten). Der Aufwand für die δ-Einstellung - hier die Längenveränderung des Peilstabes, dort die Benutzung eines eingebauten Nomogramms - hält sich die Waage.

Die Erfindung konzentriert sich in der Verwendung einer Scheibe, deren als "Gnomon" wirksame Kante die Form der Funktion u^2/3 + v^2/3 = 1 hat. Möglicherweise ging die Kenntnis dieser Funktion ihrer Verwendung in einer Sonnenuhr voraus.

<< Abb.3 Breiten-unabhängige Sonnenuhr nach Vorschlag [2]; oben: Einstellung der Stablänge, unten: Messvorgang

Eine Ausführung der Uhr nach [2] zeigt Abb.3. Die mit τ skalierte Ost/West-Schiene dient auch zur Gerad-Führung eines Blechs, an dem zu ihm senkrecht die durchsichtige Tast-Scheibe befestigt ist.

7. Künftige Breiten-unabhängige Sonnenuhren ?    ↑ Anfang

Die Relation (1) lässt noch vermuten, dass eine beliebig grosse Zahl Breiten-unabhängiger Sonnenuhren möglich sei. Diese Annahme erweist sich als viel zu optimistisch, nachdem gezeigt wurde, dass (1) auf

y' = sin τ · cos δ

zu reduzieren ist und nur folgendes bereits Gesagte ausdrückt:

Der vektorielle Anteil eines Stücks Sonnenstrahl der Länge L=L₀/cosδ beträgt in Ost/West-Richtung y'=L·sinτ. Seine Messung ist eine indirekte Messung des Stundenwinkels, worauf die geographische Breite des Mess-Ortes keinen Einfluss hat
(wohl aber die Deklination ! ).

So lange das zu verwertende Stück Sonnenstrahl auch künftig nur durch Peilung zu finden ist, werden solche "neuen" Sonnenuhren lediglich Varianten zu bisher vorhandenen, also keine wesentliche Bereicherungen sein. Feststellenswert ist, dass bereits Freeman die Peilung vereinfachte. Er konnte sie aber nicht ganz umgehen und war auf eine Ebene als "Zifferblatt" angewiesen, obwohl die zu bestimmende y-Koordinate als Gerade auf ein Stab-förmiges Gebilde zielt.

8. Literatur  ↑ Anfang

[1] J.G.Freeman: "A latitude-independent sundial", J.Roy.Astron.Soc.Can., Vol.72, No.2, 1978
[2] Deutsche Gesellschaft für Chronometrie: "Sonnenuhren Handbuch", 2006

9. Anmerkung  ↑ Anfang

Die von Freeman verwendete Vorrichtung projiziert den Sonnenort auf das Zifferblatt, was typisch für eine "geometrische" [2] Sonnenuhr ist. Untypisch dabei ist aber, dass die Projektionsvorrichtung in die Sonne gedreht werden muss. Wegen der nötigen Auswertung mittels Nomogramm gehört sie zu den "Nomogramm-Sonnenuhren" [2]. Dass der Schatten-werfende Punkt mit der Sonnen-Höhe variiert, ist von der Analemmatischen Sonnenuhr bekannt, ist also keine Besonderheit an Freeman's Vorrichtung.

Siegfried Wetzel, CH 3400 Burgdorf, Dezember 2007