<< Home
<< andere Sonnenuhren-Beiträge
↓↓ Ende
Sonnenuhren mit Lichtbrechung
siehe auch : Sonnenuhren mit Lichtbrechung (Vortrag)Inhalt
1. Abbildung des gesamten Himmels auf begrenzter ebener Fläche2. Anwendung der gebrochenen gnomonischen Projektion bei ebenen Sonnenuhren
2.1 Eine horizontale Sonnenuhr auf dem Boden eines Badebeckens
2.2 Eine vertikale Sonnenuhr auf der Rückseite eines Blocks aus durchscheinendem Kunststoff
3. Wie groß ist die Verzerrung bei gnomonisch-gebrochener Projektion?
4. Die durch Brechung veränderte Form der Stunden- und Deklinationslinien
4.1 Die durch Brechung veränderte Form der Stundenlinien
4.2 Die durch Brechung veränderte Form der Deklinationslinien
5. Zusammenfassung
6. Literatur
7. Anmerkungen
8. Anhänge
8.1 Die durch Brechung veränderte Form des Wendekreis des Krebses bei φ = 0°
8.2 Beispiel einer ausführlichen Konstruktion einer gnomonisch-gebrochenen Projektion
8.3 Ein weiterer Prototyp einer Sonnenuhr mit Lichtbrechung
1. Abbildung des gesamten Himmels auf begrenzter ebener Fläche
Bei einer Sonnenuhr mit schattenwerfendem Punkt oder lichtdurchlassendem Loch wird der Himmel in gnomonischer Projektion (das abbildende Element befindet sich im Mittelpunkt der Himmels-Sphäre) abgebildet. In der üblicherweise auf ein ebenes Zifferblatt erfolgenden Abbildung - z.B. in einer horizontalen Sonnenuhr - fehlen die Randteile des Himmels, weil sie außerhalb der Grenzen eines endlich großen Zifferblatts liegen.
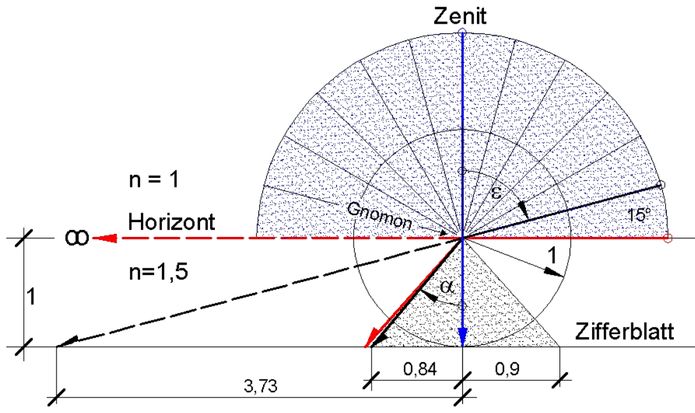 Abb.1 Abbildung des Himmels mit
Abb.1 Abbildung des Himmels mit
einer gnomonischen
Horizontal-Sonnenuhr
Brechungsindex des Mediums
zwischen Gnomon und Zifferblatt:
n= 1,5: Bildgröße = 1,8
(n= 1,0: Bildgröße → ∞)
Hingegen wird der gesamte Himmel (Raumwinkel 180°, oben) "auf einer begrenzten ebenen Fläche" [1] abgebildet, wenn das Licht am Gnomon in ein optisch dichteres Medium (dichter als Luft) "hineingebrochen" wird. In Abb.1 ist das für ein Medium mit Brechungsindex n=1,5 (in etwa Acrylglas) dargestellt: Die Ausdehnung des Himmelsbildes ist nur etwa das 1,8-fache (2 · 0,9; Raumwinkel etwa 82½°) der Gnomon-Höhe.
Der Himmel ab 15° über dem Horizont hat im Bild die Ausdehnung des 1,68-fachen (2 · 0,84) der Gnomonhöhe.
Der Zusammenhang zwischen dem Eintrittswinkel ε und dem Austrittswinkel α eines Lichtstrahls an der brechenden Grenzfläche wird vom Snellius'schen Brechungsgesetzt dargestellt:
sin ε / sin α = n1 / n2 . I.d.R ist n1 = 1 (Luft). Damit und mit einer Umstellung wird es hier wie folgt angewendet:
sin α = sin ε / n .
 Abb.2 Zwei Sonnenuhrenzifferblätter für gnomonisch gebrochene Abbildung des Sonnenstandes links: auf dem Boden eines mit Wasser zu füllenden Beckens [1] rechts: auf der Rückseite eines Blocks aus Kunststoff [2]
Abb.2 Zwei Sonnenuhrenzifferblätter für gnomonisch gebrochene Abbildung des Sonnenstandes links: auf dem Boden eines mit Wasser zu füllenden Beckens [1] rechts: auf der Rückseite eines Blocks aus Kunststoff [2]
2.1 Eine horizontale Sonnenuhr auf dem Boden eines Badebeckens
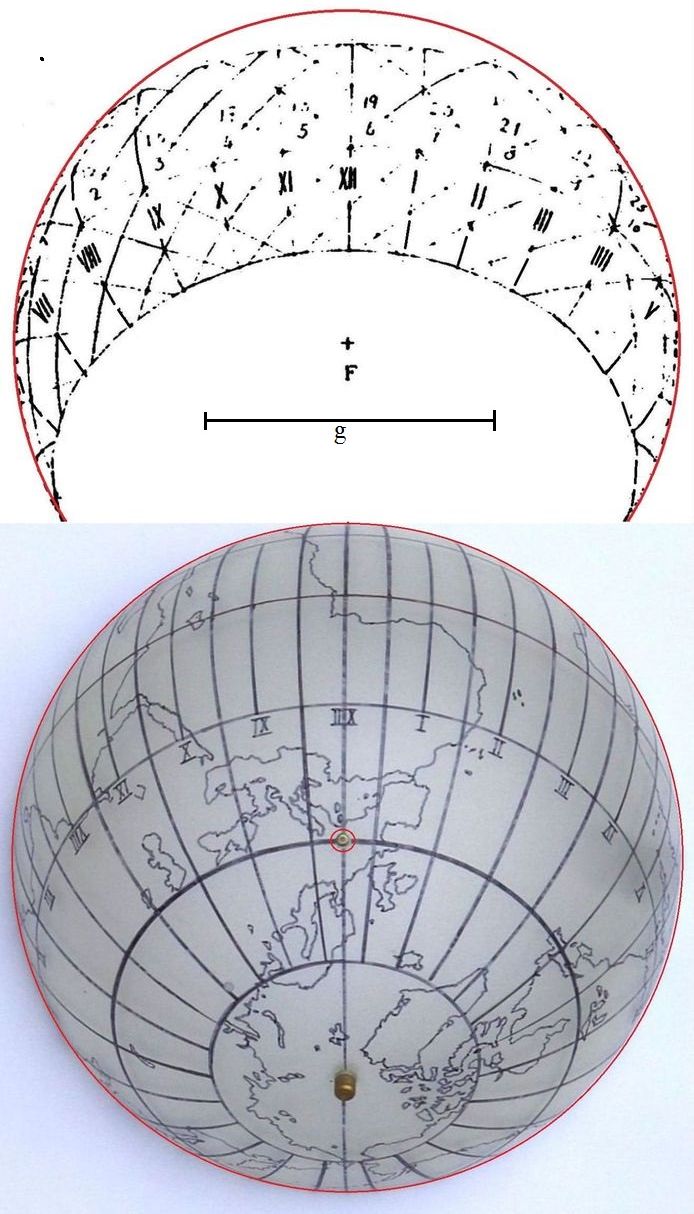 Abb.3 Sonnenuhren-Zifferblatt
Abb.3 Sonnenuhren-Zifferblatt
unter Wasser (n=1,33)
römische Ziffern für äquinoktiale
Stunden,
gekreuzt darüber babylonische
und italienische Stunden
[1] (Anmerkung 2)
überlagert: Himmel und Erde
(φ=47° für z.B. Bern=Bildmitte)
(Anmerkung 3)
Schilt schreibt:
"Die gnomonische Abbildung wird durch die Brechung der Lichtstrahlen derart verzerrt, dass alle Bildpunkte gegen F hin verschoben" sind. "Man kann an dieser Sonnenuhr den vollständigen täglichen ... Lauf der Sonne auf einer begrenzten ebenen Fläche beobachten."
In einer kürzlich erschienene Publikation [2] heisst es sinngemäß:
Die "Orginalität liegt in der Ausbildung der Stundenlinien, welche die Erde und ihr Längennetz visuell darstellen." Mit anderen Worten: Der Himmel und die Erde werden vollständig auf einer kreisförmig begrenzten ebenen Fläche dargestellt. Die Stundenlinien bzw. die Längenkreise der Erde erscheinen als Ellipsen, deren gemeinsamer Umkreis das Bild des Himmels bzw. der Erde begrenzt (Abb.5).
a.jpg) Abb.4a Nachbau der Wasser-Sonnenuhr von Schilt,
Abb.4a Nachbau der Wasser-Sonnenuhr von Schilt,
noch ohne Wasser [5]
Schilt hat der horizontalen Sonnenuhr mit dem Zifferblatt auf dem "Boden seines Badeweihers" keine Erdkarte unterlegt. Ein verkleinerter Nachbau (Wasser-Kübel anstatt -Becken) der Schilt`schen Sonnenuhr mit unterlegter und passend verzerrter Erde-Karte (Abb.4a)wurde kürzlich bekannt [5].
2.2 Eine vertikale Sonnenuhr auf der Rückseite eines Blocks aus durchscheinendem Kunststoff
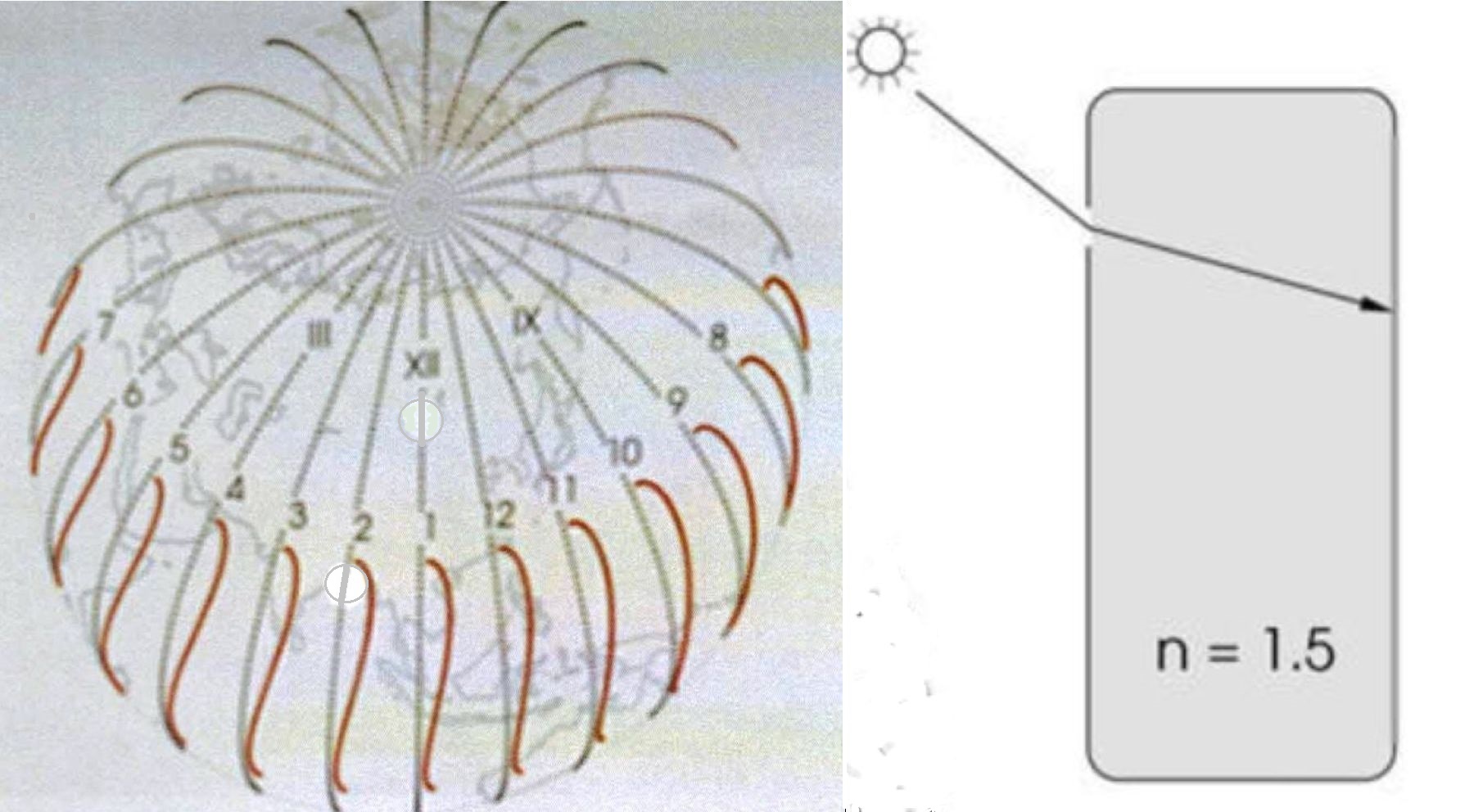 Abb.5 Sonnenuhren-Zifferblatt
Abb.5 Sonnenuhren-Zifferblatt
hinter Kunststoff (n=1,5) [2]
Das Zifferblatt enthält auch keine Deklinations- bzw. Breitengradslinien. Hingegen ist die Behandlung der Stunden- bzw. Längengradlinien wesentlicher Bestandteil dieser Arbeit. In ihr wird der Nachweis erbracht, dass sie Teile von Ellipsen sind.
Ab dem nächsten Abschnitt 3. wird die Form beider Linienarten behandelt.
Bei Vergleich zwischen den Abb.n 3 und 6 ist die Güte der Annäherung zwischen beiden Darstellungen (orthographische Projektion der Erde und gnomonisch-gebrochene Projektion des Himmels) erkennbar. Sie ist nicht ausreichend gut, so ist u.a. die Breite des Gürtels zwischen den Wendekreisen in Abb.3 deutlich größer als in Abb.4. Für den praktischen Gebrauch einer solchen mit dem Bild der Erde ergänzten Sonnenuhr muss letztere verzerrt werden. Die nötige Verzerrung wird umso kleiner je größer der Brechungsindex des brechenden Mediums zwischen Nodus und ebenem Zifferblatt ist (siehe Abb.6, Anmerkung 5).
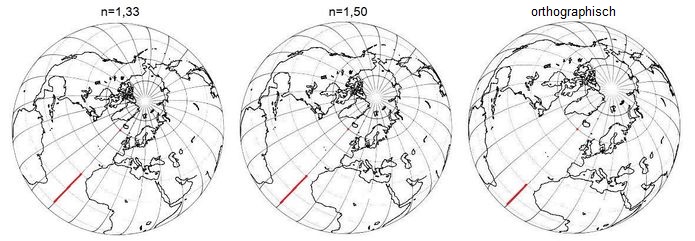 Abb.6 verzerrtes Bild der Erde bei gebrochener (n=1,33 und n=1,50) gnomonischer Projektion (Anmerkung 6) und
Abb.6 verzerrtes Bild der Erde bei gebrochener (n=1,33 und n=1,50) gnomonischer Projektion (Anmerkung 6) und
Bild bei orthographischer Projektion [2]
3. Wie groß ist die Verzerrung bei gnomonisch-gebrochener Projektion?
Die Verzerrung des Liniennetzes aus Stunden- und Deklinationslinien auf der Himmelskugel geht beim Übergang zur Darstellung in der Ebene zur Änderung der Linienformen parallel, beides ist nicht voneinander trennbar. Im Folgenden wird dennoch ezunächst die Verzerrung auf dem Meridian an ein paar besonderen Punkten im Vergleich zur orthographischen Projektion quantitaiv bestimmt, bevor zur geänderten Form der Linien übergegangen wird.
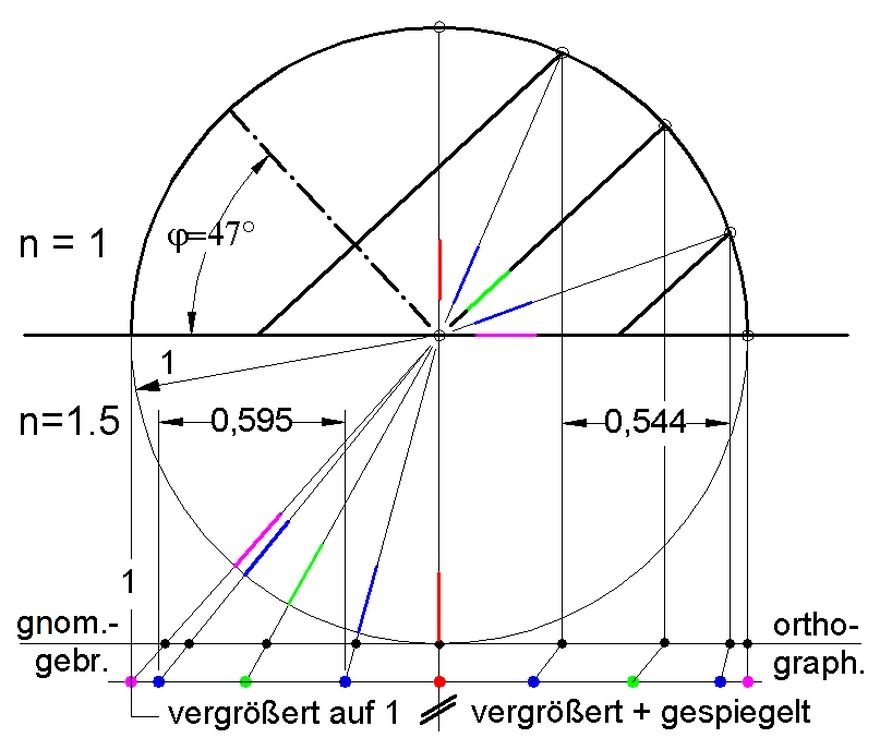 Abb.7 Ermittlung der Verzerrung:
Abb.7 Ermittlung der Verzerrung:
dargestellt an ausgewählten Meridian-Punkten
(Schnittpunkte mit Himmels-Äquator und
Wendekreisen)
n=1,50, φ = 47°
In Abb.7 sind zwei Projektionen von Meridian-Punkten (Nord-Süd-Mittagsbogen am Himmel) auf eine horizontale Ebene dargestellt. Die gnomonisch-gebrochene Projektion befindet sich unten links (siehe auch Abb.1) und die orthographische unten rechts.
Die gnomonisch-gebrochen projizierte Strecke (links: kleine schwarze Punkte) wurde zum Vergleich mit der Punkteverteilung in der orthographisch projizierten Strecke (rechts: schwarze Punkte) in Einheitslänge 1 ebenfalls auf diese Länge vergrößert (links: farbige Punkte). Schließlich wurde gnomonisch-gebrochen projizierte Strecke für einen einfach erkenbaren Vergleich mit der orthographisch projizierten Strecke nach rechts hinüber gespiegelt.
Die durch gnomonisch-gebrochene Projektion erhaltene Strecke ist in ihrem mitteren Bereich gedehnt (was in den Endregionen durch örtliche Stauchung wieder ausgeglichen wird). Die in Abb.3 durch Vergleich mit Abb.4 erkennbare Verzerrung wird bestätigt und quantitativ angegeben:
Die Breite des Gürtels innerhalb der Wendekreise wird auf das etwa 1,1-fache gedehnt (0,595/ 0,544 = 1,09;
n=1,50; φ=47°). Der Gürtel liegt näher beim Zentrum (roter Punkt) als bei orthographischer Projektion. Siehe auch die Gürtelbreite und -lagen (rote Strecken) in Abb.6.
4. Die durch Brechung veränderte Form der Stunden- und Deklinationslinien
Im vorherigen Abschnitt 3. wurde die nicht unwesentliche Verzerrung in einer Dimension, nämlich auf dem Meridian nachgewiesen. Im Folgenden soll untersucht werden, wie gut die Ähnlichkeit des gnomonisch-gebrochen projizierten Himmels im Allgemeinen - d.h. in beiden Dimensionen - mit einem orthographisch projizierten Bild des Himmels und der Erde ist. Dabei geht es im Besonderen darum, ob die Stunden- und Deklinationskreise als Ellipsen abgebildet werden, oder welche Abstriche davon gemacht werden müssen.
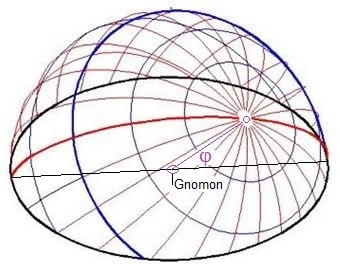 Abb.8 Die Koordinaten-Kreise am Himmel
Abb.8 Die Koordinaten-Kreise am Himmel
(ortsfestes Äquatorialsystem)
rot: Stunden-; blau Deklinations-Kreise
(schwarz: Horizont)
Im als sphärische Fläche angenommenen Himmel sind die Stundenlinien (τ =konst.) halbe Großkreise (rot in Abb.8) und die Deklinationslinien (δ =konst.) Kleinkreise (blau) oder Teile von ihnen (je nach geographischer Breite φ).
In orthogonaler Projektion auf eine Ebene sind sie halbe Ellipsen bzw. ganze Ellipsen oder Stücke von ihnen (Abb.4). Ob sie das in gnomonischer Projektion mit Brechung auch oder näherungsweise auch sind, ist zu untersuchen.
Die auf Sonnenuhrenzifferblättern enthaltenen Stunden- und Deklinationslinien sind i.d.R. nur ziemlich kleine Teile der ursprünglichen Kreise. Wegen der besseren Erkennbarkeit werden im Folgenden immer die Abbildungen ganzer Kreise gezeigt.
4.1 Die durch Brechung veränderte Form der Stundenlinien
Die Stundenkreise sind Großkreise. Weil sie alle gleich groß sind und sich ihre Mittelpunkte im gnomonischen Projektionszentrum befinden, ist zu erwarten, dass sich ihre Abbildung - auch gnomonisch-gebrochen - als einfacher verständlich als die der Deklinationskreise erweist. Die Mittelpunkte der Deklinationskreise (Ausnahme: der Himmelsäquator) befinden sich abseits des Projektionszentrums (lediglich alle auf der Himmelsachse). Erwartet werden kann auch, dass die Formänderung der Großkreise beim Abbilden milder ausfällt als die der Kleinkreise mit abseits liegenden Mittelpunkten und zusätzlich noch veränderlichen Durchmessern.
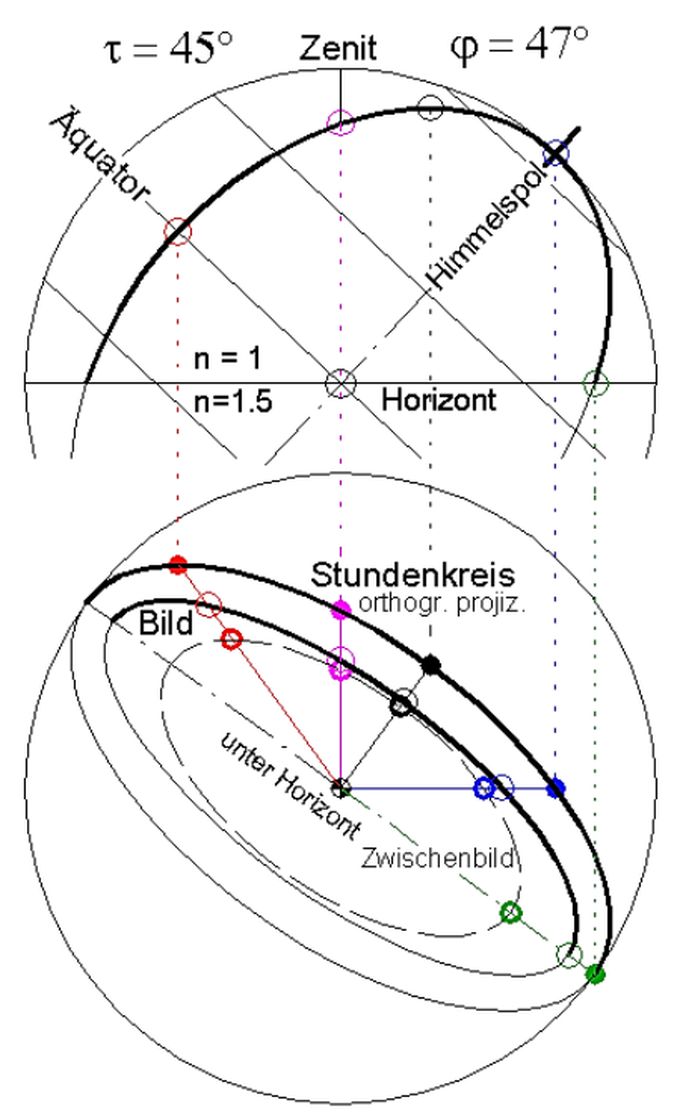 Abb.9 gnomonisch-gebrochene Projektion (n=1,5)
Abb.9 gnomonisch-gebrochene Projektion (n=1,5)
eines Stundenkreises (τ=45°)
auf horizontale Bildfläche
Beobachtungsort: φ=47°
ausführliche Konstruktion: s. Anhang 2
Die von einem Stundenkreis kommenden, alle in einer Ebene (Stundenebene) verlaufenden Lichtstrahlen werden im Projektionszentrum beim Übergang ins optisch dichtere Medium gebrochen. Danach befinden sie sich auf der Mantelfläche eines Kegels mit elliptischem Querschnitt. Auf einer gedachten, die ebene Bildfläche (zur Trennfläche zwischen den beiden optisch verschieden wirkenden Stoffen parallel) der Einfachheit halber berührenden sphärischen Bildfläche wird der Stundenkreis als Ellipse abgebildet. Diese ist gemäß Snellius'schem Brechungsgesetz lediglich verkleinert ähnlich derjenigen Ellipse, die bei orthographischer Projektion auf der Bildebene entsteht (Zwischenbild). Die gnomonisch-gebrochene Abbildung ist von der gedachten sphärischen Bildfläche aus weiter bis zur Bildebene zu verfolgen. Dabei werden alle vom Ellipsen-Mittelpunkt ausgehenden, zu Ellipsen-Punkten zeigenden Vektoren mit dem Faktor tanα / sinα (α = Austrittswinkel der Lichtstrahlen am brechenden Punkt / Gnomon) verlängert. Dieser Faktor ist zwar nicht konstant, die Ellipsenform bleibt aber erhalten. Das kann daraus gefolgert werden, dass bei φ = 0° und
τ = 90° der Grenzfall Kreis auch als Kreis abgebildet wird. Verändert ist lediglich das Achsenverhältnis a/b im Vergleich zur bei orthographischer Projektion entstehenden Ellipse. Im Beispiel von Abb.9 wird die gnomonisch-gebrochen entstehende Ellipse etwa 25% schlanker. Bei
φ = 0° entstehen dickere Ellipsen im Bild: τ = 30°: 27% verdickt; τ = 60°: 10% verdickt.
In der Arbeit [2] (2019) ist der Nachweis geschlossen erbracht: Ellipsengleichung für die gebrochene gnomonische Projektion eines Stundenkreises, (A6) .
4.2 Die durch Brechung veränderte Form der Deklinationslinien
In der Arbeit [2] wird darauf nicht eingegangen.
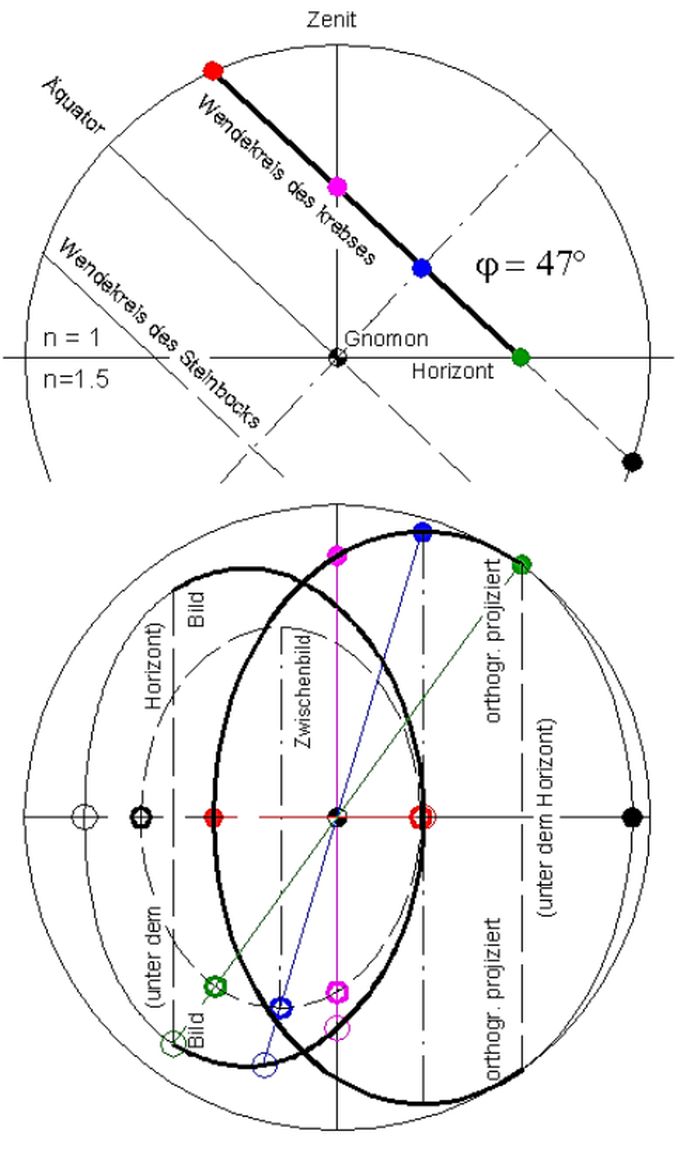 Abb.10 gnomonisch-gebrochene Projektion (n=1,5)
Abb.10 gnomonisch-gebrochene Projektion (n=1,5)
des Wendekreis des Krebses (δ=+23,5°)
auf horizontale Bildfläche
Beobachtungsort: φ=47°
Im Unterschied zu den Stundenkreisen haben die Deklinationskreise keine besondere Lage relativ zum Gnomon: Ihre Mittelpunkte decken sich nicht mit dem Gnomon. Die von einem Deklinationskreis zum Gnomon gehenden Lichtstrahlen befinden sich bereits auf einem Kreiskegel-Mantel (Deklinationskegel) und nachher im optisch dichteren Medium auf dem Mantel eines elliptischen Kegels. Unterschiedslos zu den Stundenkreisen werden die Deklinationskreise in der gedachten sphärischen Bildfläche ebenfalls als Ellipsen abgebildet. Ein Unterschied tritt erst bei der Weiterverfolgung dieses Zwischenbildes hin zur ebenen Bildfläche auf. Die tanα/sinα-Verlängerung betrifft hier nicht die regulären Ellipsenpunkt-Radien (vom Ellipsen-Mittelpunkt ausgehende Vektoren) sondern von einem exzentrischen Punkt ausgehende Vektoren. Der variierende Verlängerungsfaktor ist nur noch für je 2 Punkte gleich. Die Ellipse wird in eine geschlossene Kurve verzerrt, die nur noch aus zwei spiegelbildlich gleichen Teilen besteht (Abb.10).
5. Zusammenfassung
Mein erster Eindruck bei der neuerlichen Erwähnung [2] von Schilt's Sonnenuhr im Wasser, eine gleichwertige Alternative z.B. zur HELIOS kennen gelernt zu haben, hat sich nicht bestätigt. Das bei gnomonisch-gebrochener Projektion zu verwendende Zifferblattnetz ähnelt nur schwach dem Netz aus orthographisch projizierten Längen- und Breitengraden der Erde. Im Vergleich zur einfachen gnomonischen Projektion dieser Linien und der Grenzen zwischen Festland und Meeren der Erde ist der Gewinn deutlich. Es verbleibt aber immer noch eine erhebliche Irritation, wenn man sich anhand dieser Darstellung der Erde orientieren, z.B. den Subsolaren Punkt verfolgen will. Das Erdebild ist noch zu stark verzerrt. Am stärksten sind die Breitengrade (Deklinationslinien) betroffen, sie weichen deutlich von elliptisch geformten Linien ab. Die Längengrade (Stundenlinien) sind weniger verzerrt. Sie sind sogar elliptisch, haben nur eine andere Krümmung und sind seitlich verschoben. In den späteren als in der Schilt'schen Wasseruhr wird vorwiegend Acrylglas als höher brechendes Material (n=1,5) verwendet. Die Verzerrung ist dabei geringer, aber bei weitem noch nicht ausreichend. Optisch dichte Materialien gibt es ohnehin höchstens bis n=2. Sie sind teuer, und da bei größerem Brechungsindex die Schichtdicke vergrößert werden muss, würden die Kosten exponentiell ansteigen, ohne wesentliche Verbesserung erreicht zu haben.
Die "Sonnenuhr mit Stundenlinien in Erdgestalt" [2] ist eine bemerkenswerte kompakte Sonnenuhr (Abb.11, links). Sie hat die Form eines flachen Würfels (Würfelsonnenuhr), an den nicht wie sonst üblich ein Polstab oder eine Gnomon vorgebaut ist. Die dadurch fehlende Sperrigkeit ist ein Vorteil für solche auf einer Fensterbank, einer Balkonbrüstung oder auf einem Gartentisch aufzustellende Sonnenuhren. Die zum Vergleich rechts in Abb.11 gezeigte, auch von der Rückseite ablesbare tragbare Vertikalsonnenuhr ist wegen des durchgehenden Polstabs noch etwas sperriger, aber mit dem Vorteil, dass auf diese Weise zusätzlich das Ablesen der frühen Morgen- und späten Abendstunden im Sommer möglich ist.
Die Stundenlininien in Erdgestalt weisen darauf hin, dass eine geometrische Gleichheit zwischen der (gedachten) Himmels- und der Erdkugel besteht. Mehr ist auf der von hinten abzulesenden Würfelsonnenuhr nicht möglich.
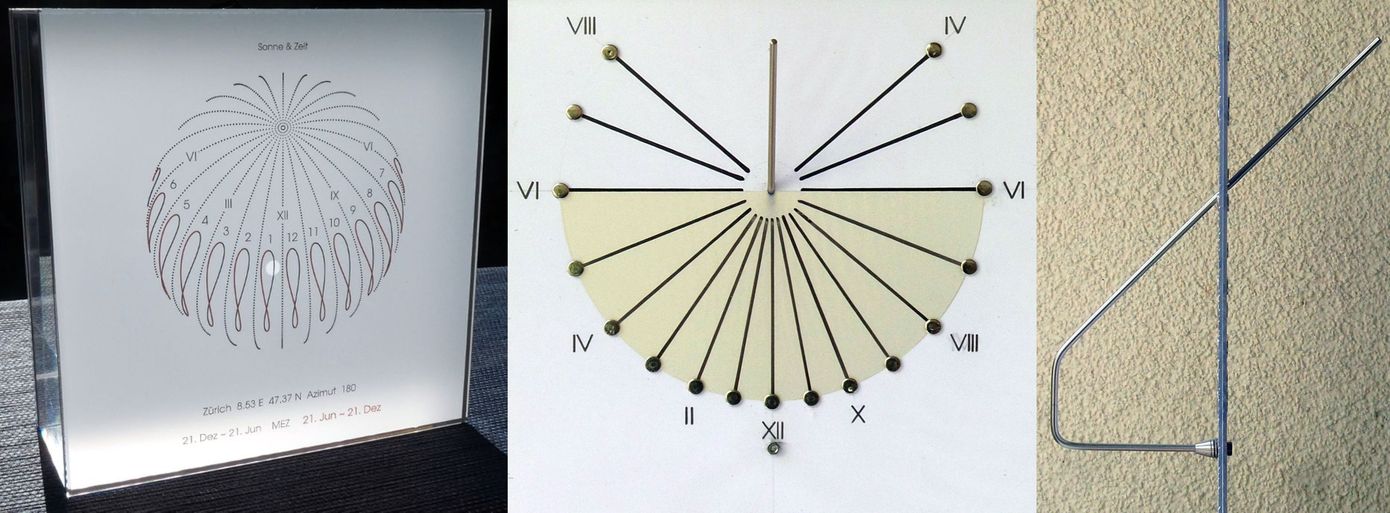 Abb.11 "Eine Sonnenuhr mit Stundenlinien in Erdgestalt" [2]
Abb.11 "Eine Sonnenuhr mit Stundenlinien in Erdgestalt" [2]
im Vergleich mit einer ebenfalls vertikalen und von der Rückseite abzulesenden Sonnenuhr mit Polstab:
Stabschatten zwischen VI und VI Uhr auf durchscheinender Mattscheibe,
direkt ablesbarer Stabschatten in den frühen Morgen- und späten Abendstunden im Sommer
6. Literatur
[1] Heinz Schilt: Ebene Sonnenuhren, Eigenverlag, 8. Auflage, 1994, Seiten 30 bis 32[2] Joachim Heierli: Eine Sonnenuhr mit Stundenlinien in Erdgestalt, Deutsche Gesellschaft für Chronometrie,
Jahresschrift 2020, Band 59, Seiten 181 bis 189
A sundial with hour lines portraying the Earth, American Journal of Physics 87 (12), 2019
[3] Siegfried Wetzel: Der Subsolare Punkt auf einer Globus-Sonnenuhr, 4. Die HELIOS, eine .. Globus-Sonnenuhr
[4] Siegfried Wetzel: Eine Reflex-Globus-Sonnenuhr, 3. Eine Reflex-Globus-Sonnenuhr
[5] Ernst Lobsiger: "Auf den Spuren von Heinz Schilt", Bild-Vorwegnahme aus der voraussichtlich im Okt. 2024
und unter diesem Titel öffentlich zugänglichen Arbeit
7. Anmerkungen
Anmerkung 1:Bei Verwendung eines Polstabes ist das im Prinzip gleich. Der Polstab enthält aber unendlich viele Gnomone in unendlich vielen Höhen. Sonnenauf- und -untergang werden vom Schatten eines Punktes nahe beim Stabfußpunkt, also von einem sehr niedrigen Gnomon angezeigt. Der Schatten befindet sich relativ zu dieser kleinen Gnomonhöhe ebenfalls am Rand eines sehr großen, absolut aber "annehmbar" großen Zifferblatts. Je höher die Sonne steht, ein umso höher liegender Bereich des Stabes - im Extrem seine Spitze, der Gnomon - wird zur Anzeige benutzt, und die ausgelegte Breite des Zifferblattes reicht dafür aus, ist "angemessen".
Anmerkung 2:
Es handelt sich um das später erneuerte und erweiterte Zifferblatt im Becken von Abb.2, links.
Anmerkung 3:
Abb.4 enhält ein Foto meiner Reflex-Globus-Sonnenuhr. Diese Kugel ist mit langer Brennweite aufgenommen, so dass das Bild mit guter Näherung eine orthographische Projektion darstellt (Bildwinkel der Kugel nur etwa 2,5°).
Anmerkung 4:
"Eine mit einem Erde-Bild komplettierte Sonnenuhr von Schilt stellt die himmelsmechanische Beziehung zwischen Erde und Sonne praktisch selbsterklärend dar" [2] ist nur bei einigen der dort gezeigten und a.a.Stelle auch zum Verkauf angebotenen Sonnenuhren vorgesehen, ist aber nicht gelungen, weil die unterlegten Erde-Karten in keinem Fall passen. Bei vertikalen Sonnenuhren ist die Selbsterklärung beeinträchtigt, da die gnomonisch abgebildete Himmelssphäre (Halbkugel) sich zur Häfte unter dem Horizont befindet. Das hat zur Folge, dass das Sonnenuhrenzifferblatt auch nur eine Halbkreisfläche bedeckt (Abb.12, das Abbbild der Sonne erreicht im Gegensatz zu horizotalen Sonnenuhren die andere Hälfte nie; bei Letzteren aber im Sommer in den frühen Morgen- und den späten Abendstunden).
Ein ganz wesentlicher Nachteil einer von der Rückseite zu betrachtenden vertikalen Sonnenuhr ist, dass eine dem Zifferblatt unterlegte Erde-Karte, auf der der Subsolare Punkt angezeigt wird, spiegelverkehrt sein muss.
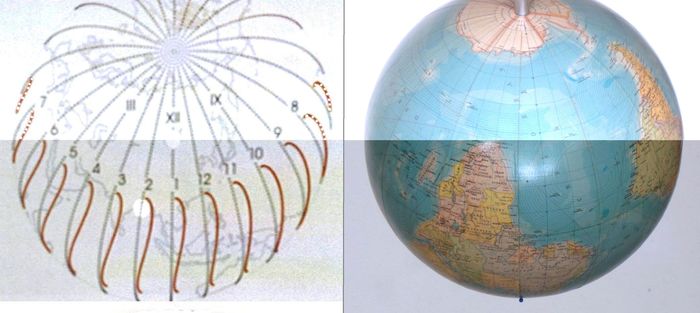 Abb.12 vertikale Sonnenuhr: Zifferblatt hinter Kunststoff (s.a. Abb.5) und dazu passendes Bild der Erde; φ = 48°
Abb.12 vertikale Sonnenuhr: Zifferblatt hinter Kunststoff (s.a. Abb.5) und dazu passendes Bild der Erde; φ = 48°
links: Zifferblatt
rechts: Bild der Erde aus dem Zenit über dem Ort φ = -42°, λ = +10°,
muss noch passend verzerrt und um die Vertikale gespiegelt werden
Anmerkung 5:
Die Verzerrung (vergl. Längen der roten Striche für einen 30° breiten Gürtel über dem Äquator) ist auch bei n=1,50 (Acrylglas) noch nicht wesentlich kleiner. Selbst bei exotischen Werkstoffen bleibt der Brechungsindex kleiner als n=2, was dennoch nicht ausreichen würde, um auf das Anpassen des Erde-Bildes an das verzerrte Himmelsbild verzichten zu können. Die Anpassung ist im Wesentlichen für die Ablesegenauigkeit des Subsolaren Punktes erforderlich, Abstriche bei der Genauigkeit des Bildes außerhalb des Gürtels zwischen den Wendekreisen könnte man hingegen leicht hinnehmen. Diese Bereiche haben nur die Funktion, die Sonnenuhr zu schmücken, ihr einen Globus überzustülpen, der nicht besonders genau sein muss.
Anmerkung 6:
Die Abbildungen sind zu klein, um die Auswirkung der Verzerrung auf die Form der Längen- und insbesondere auf die der Breitenkreise beurteilen zu können.
8. Anhänge
8.1 Die durch Brechung veränderte Form des Wendekreis des Krebses bei φ = 0
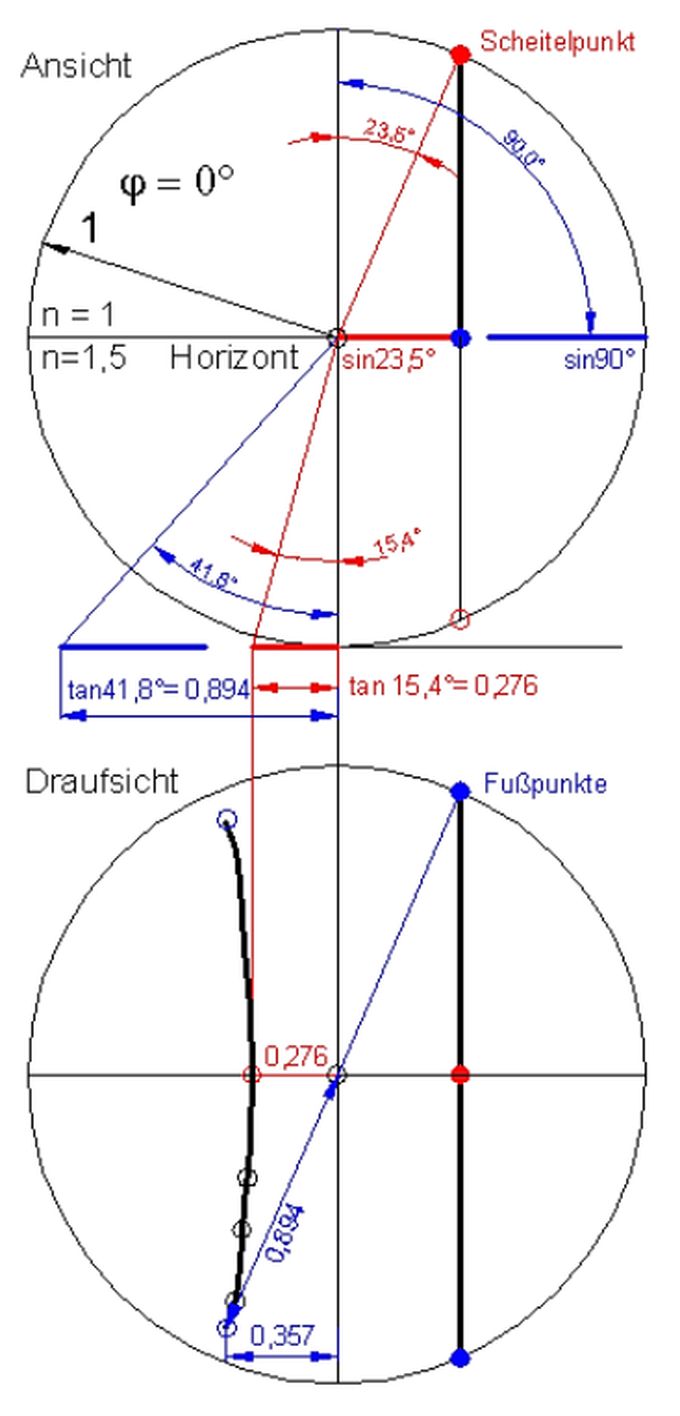 Abb.Anhg.1
Abb.Anhg.1
gnomonisch-gebrochene Projektion des nördlichen Wendekreises an einem Beobachtungsort auf dem Äquator (φ=0°)
Ausführliche Darstellung der Konstruktion der in Ab.8 gezeigten gnomonisch-gebrochenen Projektion.
Anstatt der erwarteten Gerade ist das Bild des Wendkreises eine deutlich gebogene Linie.
Es wurden wurden insgesamt 5 Quer-Abstände ermittelt:
0,276 - 0,291 - 0,309 - 0,330 - 0,357.
Diese Konstruktion hatte ich als erste von der gnomonisch-gebrochenen Projektion eines Deklinationskreises gemacht. Sie gab mir sofort einen Hinweis darauf, dass Deklinationskreise verzerrt abgebildet werden. Dass hingegen der im Meridian liegende Stundenkreis (τ = 0°) als Gerade abgebildet wird, ist nicht als Hinweis dafür ausreichend, dass alle Stundenkreise Ellipsenform im Bild annehmen.
8.2 Beispiel einer ausführlichen Konstruktion einer gnomonisch-gebrochenen Projektion
eines Stundenkreises
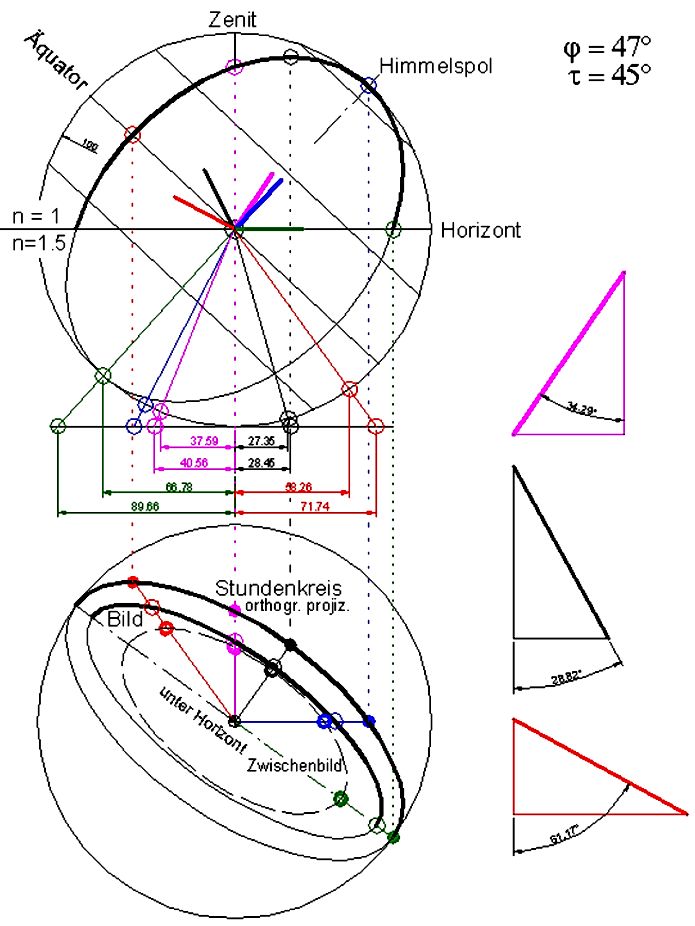
Abb.Anhg.2 Ausführliche Darstellung der Konstruktion der in Ab.8 gezeigten gnomonisch-gebrochenen Projektion.
unten links: Objekt, Zwischenbild und Bild
rechts: Konsruktion einiger Einfallswinkel ε
oben links: Ansicht aus Ost,
überlagert ist die Konstruktion der Strahl-Brechung in einigen dagegen um die Vertikale
verdrehten Ebenen (grün, schwarz, magenta und rot)
8.3 Ein weiterer Prototyp einer Sonnenuhr mit Lichtbrechung
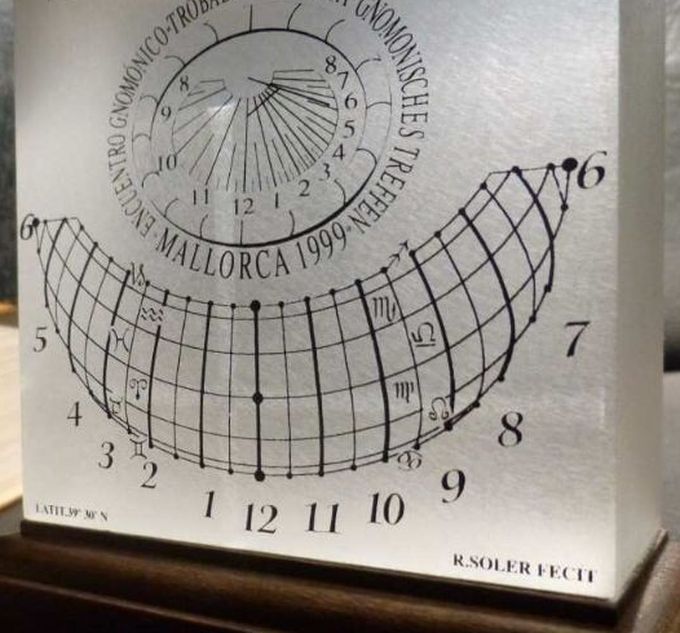 Abb.Anhg.3 Prototyp einer horizontalen Sonnenuhr
Abb.Anhg.3 Prototyp einer horizontalen Sonnenuhr mit Lichtbrechung, φ = 39,5°
Konstruktion: Rafael Soler Gayá (E)
Eigentum und Foto: Rolf Wieland (D)
Diese Sonnenuhr stammt aus dem Jahre 1999 (eine weitere hat Fred Sawyer (USA) 2012 vorgestellt). Sie zeigt, dass die Idee von Schilt nicht erst kürzlich erneut wieder aufgenommen und dass damals schon der vertikale Typ gebaut wurde.
Sie reicht von 6 Uhr bis 6 Uhr, berücksichtigt also streng, dass ihre nach Süden auszurichtende Vorderseite außerhalb dieses Zeitraumes unbesonnt bleibt.
Die Darstellung im Oberteil ist keine anzeigende zweite Sonnenuhr sondern lediglich das Signet der Veranstaltung, für die sie angefertigt wurde.
![]() Siegfried Wetzel, CH 3400 Burgdorf, Oktober 2020 (Aug. 2024)
Siegfried Wetzel, CH 3400 Burgdorf, Oktober 2020 (Aug. 2024)