<< Home
<< andere Sonnenuhren-Beiträge
 ↓↓ Ende

Sonnenuhren mit besonderen Polstäben

Inhalt

1. Bernhardt-Sonnenuhr und Hollander-Sonnenuhr
2. Analemma der Zeitgleichung, Nodus-Verschiebung bei Sonnenuhren zur Anzeige der mittleren Sonnenzeit
3. Funktion der Bernhardt-Sonnenuhr
4. Funktion der Hollander-Sonnenuhr
5. Hollander-Sonnenuhr mit Doppelkegel
6. Literatur
8. Anmerkungen

1. Bernhardt-Sonnenuhr und Hollander-Sonnenuhr  ↑

Die Bernhardtsche Sonnenuhr (auch Bernhardtsche Walze, Abb.1, von Martin Bernhard nach einer älteren britischen Erfindung ab 1966 in mehreren Sückzahlen gebaut) ist die ältere und bekanntere von zwei Sonnenuhren, die mit Hilfe eines besonders geformten relativ dicken Polstabs die mittlere Sonnenzeit anzeigen. Die zweite dieser Sonnenuhren wurde vom Niederländer Hendrik Hollander erfunden und 2006 [1] vorgestellt (Abb.2).

Abb.1  Sonnenuhr von Bernhardt, Walze für erstes Halbjahr (Dez.-Juni), 11:28 MESZ (20.Mai), Bild aus Wikipedia
Abb.2  Sonnenuhr von Hollander [1]

Die Bernhardt-Uhr ist eine äquatoriale Ringsonnenuhr. Ihre ringförmige Skala liegt in der Ebene des Himmelsäquators, ihre taillierte Walze nimmt den Platz eines erdachsparallelen Polstabs ein. Ablesepunkt für die mittlere Sonnenzeit ist dort, wo der voreilende Kantenschatten der Walze die Skala kreuzt. Der schattenwerfende Punkt (Nodus) wandert auf der Walze. Über den Tag läuft er um sie, übers Jahr läuft er auf ihr (Abb.1, Dezember bis Juni) von unten (Winter) nach oben (Sommer), auf der im Sommer montierten zweiten Walze (Juni bis Dezember) von oben nach unten.

Die Hollander-Uhr ist eine ebene (horizontale) Sonnenuhr. Der fixe Nodus einer üblichen, nicht auf die mittlere Sonnenzeit korrigierten ebenen Sonnenuhr mit Stunden- und Datumslinien ist durch einen Kegel, dessen Achse vorteilhaft erdachsparallel ist, ersetzt. Auf diesem läuft er über den Tag um und übers Jahr zwischen dessen Spitze und einem nahen größten Schnittkreis hin und her. Ablesepunkt für die mittlere Sonnenzeit ist dort, wo einer der beiden Kantenschatten des Kegels eine Datumslinie und eine Stundenlinie auf dem Zifferblatt kreuzt. Da dieses nur ausgewählte Datumslinien und Stundenlinien enthält, ist in den meisten Fällen beim Ablesen zweidimensional zu interpolieren. Der Kegel wird ganzjährig benutzt. Bei nachgehender wahrer Sonne befindet sich der Nodus auf der Kegelkante, die den vorauseilenden Kantenschatten wirft, bei vorgehender wahrer Sonne auf der gegenüberliegenden Kante. Der Ablesepunkt ist für zwei Kalendertage, an denen die Sonne denselben Deklinationswinkel hat, derselbe. Das Zifferblatt sieht dem einer ebenen Sonnenuhr, die die wahre Sonnenzeit anzeigt, vor allem bei erdachsparralleler Kegelachse, sehr ähnlich. Der Unterschied ist deutlich an den Äquinoktialtagen erkennbar: Die sonst gerade Datumslinie ist bei der Hollander-Uhr leicht gegen den Fuß des Kegels gebogen (Abb.2: oberer Rand des grünen mittleren Bereichs).

2. Analemma der Zeitgleichung, Nodus-Verschiebung bei Sonnenuhren
    zur Anzeige der mittleren Sonnenzeit  ↑

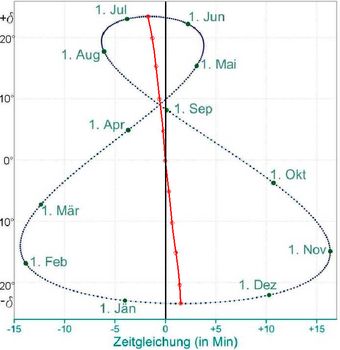Abb.3  Das Analemma der Zeitgleichung,
           links: unverzerrte Proportionen
           rechts: horizontal etwa fünffach gestreckt
                      Bild aus Wikipedia

Der Sonnenstand (Ort der wahren Sonne am Himmel) als Funktion der Sonnendeklination zu einer festen mittleren (gebräuchlichen, gesetzlichen) Tagesstunde hat die Form einer Lemniskate und wird oft als Analemma bezeichnet. Die Form dieser Kurve geht bei der Bernhardt-Uhr direkt in die Kontur der beiden Walzen ein. Bei der Hollander-Uhr gibt sie indirekt die gesamte Gestaltung, insbesondere die der Zifferblattlinien vor.

Damit die aus "falscher" Richtung scheinende wahre Sonne an derjenigen Stelle aufs Sonnenuhrenzifferblatt trifft, wo die fiktive mittlere Sonne hinfällt, wird ein gegenüber dem fiktiven Nodus der mittleren Sonne quer verschobener Nodus benutzt (Abb.4). Bei der Bernhardt-Uhr genügt diese Maßnahme zur Anzeige der mittleren Zeit. Bei der Hollander-Uhr ist die Verschiebung des Nodus nur eine von mehreren zielführenden Maßnahmen.

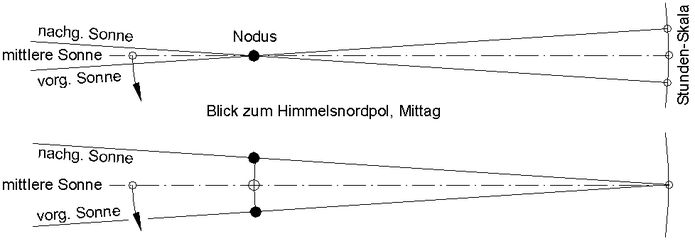Abb.4  Querverschiebung des Nodus zur Anzeige der mittleren Sonnenzeit durch die vor- bezw. nachgehende
            wahre Sonne

3. Funktion der Bernhardt-Sonnenuhr  ↑

Abb.5  Walzen der Bernhardtschen Sonnenuhr,
           links:   Walze für erstes Halbjahr (Dez.-Juni),
                      Bild aus Wikipedia
           rechts: Walze für zweites Halbjahr (Juni-Dez.),
                      Bild aus Wikipedia

Die Kontur der links abgebildeten Walze (schattenwerfende Kante ist links) entspricht dem Kurventeil von links unten bis rechts oben (linkes, unverzerrtes Teilbild in Abb.3). Die rechte Walze entspricht dem restlichen Kurventeil. Beide Walzen lassen sich nicht lückenlos aneinanderlegen, denn die beiden Kurventeile sind nur näherungsweise rechts-links-symmetrisch.

Vom Skalenring aus gesehen besteht ein Winkel von etwa zwei mal 23° zwischen unterem und oberem Walzenende. Zur Zeit um die Wintersonnenwende fällt der Kantenschatten von der unteren Walzenpartie auf die Ringskala, zur Zeit um die Sommersonnenwende stammt dieser Schatten von der oberen Walzenpartie (Anmerkung 1).

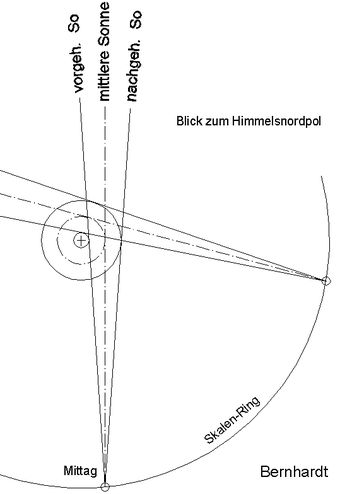Abb.6  Bernhardt-Uhr:
           Querverschiebung des Nodus zur Anzeige der
           mittleren Sonnenzeit durch die vor- bzw.
           nachgehende wahre Sonne

Die Nodi der vor- bzw. nachgehenden Sonne befinden sich auf einem kleinen und einem großen Durchmesser der Walze, deren Achse durch den Mittelpunkt der Ringskala führt. Auf diese Weise bleibt die zur Skala relative Lage des jeweiligen Nodus bei während des Tages umlaufender Sonne erhalten.

Die Nodi für vor- bzw. nachgehende Sonne befinden sich nicht auf verschiedenen Seiten der Walzenachse. Das ist ausgeschlossen, weil die Walze beim Übergang von der einen zur anderen Seite den Durchmesser null haben müsste. Die Skalierung ist für die Benutzung der bei Tagesbewegung vorangehenden Schattenkante der Walze eingerichtet.

Von Tag zu Tag wandert der Nodus zu einen parallelen Querschnittskreis der Walze, dessen Durchmesser der entsprechenden Zeitgleichung bei entsprechendem Deklinationswinkel der Sonne angepasst ist. Eine weitere Maßnahme zur Anzeige der mittleren anstatt der wahren Sonnenzeit ist bei der Bernhardt-Uhr nicht erforderlich. Da zwischen der gesetzlichen Zonenzeit und der wahren Sonnenzeit eines Ortes nur eine konstante Verschiebung besteht, lässt sich die Anzeige der Bernhardt-Uhr und anderer Uhren mit gleicher Anzeige auch auf die Zonenzeit einrichten.

4. Funktion der Hollander-Sonnenuhr  ↑

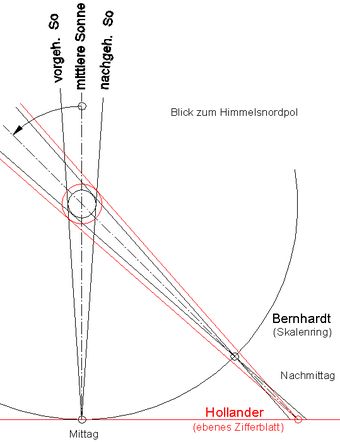Abb.7  Hollander-Uhr:
           Querverschiebung und axiale Verschiebung
           des Nodus zur Anzeige der mittleren Sonnenzeit
           durch die vor- bzw. nachgehende wahre Sonne

In Abb.7 ist in schematischer Angleichung an Abb.4 und Abb.6 gezeigt, dass der Tagesumlauf eines Nodus auf einem Kreis nur bei kreisförmigem Zifferblatt/ring und nicht bei einem ebenen Zifferblatt möglich ist. Beim ebenen Zifferblatt - wie bei der Hollander-Uhr - ist der Abstand zwischen Noduskreis und Skala nicht konstant. Ein Schattenstrahl von einem für die Mittagsstunde passenden Kreis trifft zu allen anderen Tagesstunden mit dem vom Nodus der fiktiven mittleren Sonne stammenden Strahl nicht auf einen gemeinsmen Punkt der Skala. Bei der Hollander-Uhr befindet sich der Nodus zu jeder Tagesstunde auf einem anderen Querschnittkreis des als Schattenwerfer verwendeten Kreiskegels (Abb.8, Anmerkung 2).

Die Funktion der Hollander-Uhr ist in Abb.8 unmaßstäblich dargestellt. Der anzeigende Punkt (Schnittpunkt der beiden Kantenschatten mit der Datumslinie δ, und jahreszeitlich versetzt untereinander) ist in der Regel näher bei den Schattenpunkten der Kegelspitze als bei der Fußfläche des Kegels. Analog dazu ist der die beiden Nodi N₁ und N₂ enthaltende Schnittkreis des Kegels näher bei seiner Spitze. Die Schattenpunkte der Kegelspitze sind nur an den Tagen mit Zeitgleichung=null anzeigende Punkte. Im Vergleich zu einer üblichen ebenen Sonnenuhr für die Anzeige der wahren Sonnenzeit (wahre Ortszeit WOZ), bei der die Kegelspize Nodus wäre, sind alle übrigen Anzeigepunkte und mit ihnen die sie verbindenden Datumslinien gegen die Fußfläche des Kegels (allgemein: gegen Süd) verschoben. In Abb.8 wäre die Verbindungslinie der WOZ anzeigenden Kegelspitzenschatten die Datumslinie δ für die beiden gewählten Tage.

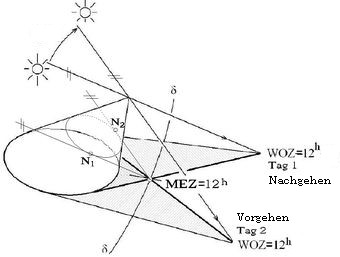Abb.8  horizontale Hollander-Uhr
           mit erdachsparallelem Kegel als Schattenwerfer
           Anzeige der mittleren Sonnenzeit (12:00 MEZ)
             an zwei Kalendertagen mit gleicher
             Sonnendeklination δ
               Tag 1: um z₁ nachgehende Sonne
               Tag 2: um z₂ vorgehende Sonne
           Bild-Vorlage: [3]

In der aus der Literatur entnommenen Abb.8 habe ich die beiden Nodi N₁ und N₂ und den gemeinsam besetzten Schnittkreis des Kegels zusätzlich eingezeichnet. Es gibt weder bei Hollander noch bei anderen Autoren ([2], [3]) einen Hinweis darauf, dass eine Sonnenuhr mit auf einem Kegel sowohl übers Jahr als auch über den Tag wandernden Nodus vorliegt, und auch keinen entsprechenden Vergleich mit der Bernhardt-Uhr, bei dem der Nodus ebenfalls wandert, und bei dem die Rundheit des Schattenwerfers auch eine Rolle spielt.

Die geometrische Behandlung als Erklärungshilfe und zur Durchführung der Konstruktion ist folgende: [2]

• Die Fußkontur des Kegels - eine Ellipse - wird mit einer der bekannten Ellipsen-Gleichungen beschrieben.
• Die beiden Anzeigepunkte für die jeweilige wahre Sonnenzeit (WOZ) an den beiden Tagen gleicher Sonnendeklination werden wie bei ebenen Sonnenuhren mit fixem Nodus beschrieben.
• Es werden Geradengleichungen für die beiden inneren Schattenkanten aufgestellt: je eine Gerade von je einem der vorher gefundenen Punkte als je eine Tangente an die Fußellipse des Kegels.
• Finden des gemeinsamen Punktes dieser Geraden: Ihr Schnittpunkt ist der gesuchte Anzeigepunkt für die mittlere Sonnenzeit (MOZ oder MEZ).

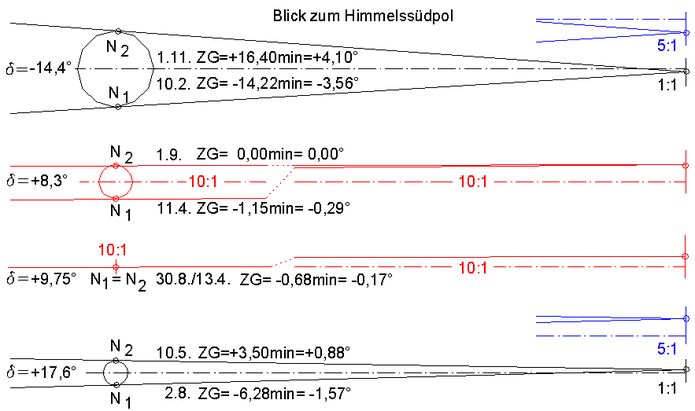Abb.9  die je 2 Zeitgleichungswerte bei ausgewählten Werten der Sonnendeklination (Anmerkung 3),
           dargestellt als Schattenstrahlen, die mit dem Schattenstrahl der zugehörenden mittleren Sonne den
           entsprechenden Winkel bilden.

In Abb.9 treffen sich je 2 Schattenstrahlen bei ausgewählten Werten der Sonnendeklination in je einem die mittlere Sonnenzeit anzeigenden Punkt. Der Winkel zwischen jedem dieser Strahlenpaare ist die Summe der als sogenannte Stundenwinkel ausgedrückten zugehörenden 2 Zeitgleichungswerte. Oben und unten handelt es sich um die δ-Fälle, in denen die beiden Schlingen des Zeitgleichungs-Analemmas (Abb.3) größte horizontale Ausdehnung haben. In der Mitte sind Tagespaare aus dem Kreuzungsbereich des Analemmas relativ zu den bisherigen Paaren in 10-facher Vergrößerung dargestellt. In die Strahlenpaare ist jeweils ein Kreis mit den beiden Nodi N₁ und N₂ gesetzt, womit der Übergang zur Hollander-Uhr hergestellt ist. Im Teilbild für den Analemma-Kreuzungspunkt (δ=+9,75°) befinden sich die beiden Nodi an der gleichen Stelle, nämlich in der Kegelspitze (Anmerkung 4). Der Kreis im oberen Teilbild ist der größte bzw. derjenige mit dem größten Abstand von der Kegelspitze (bei einer bestimmten Tagesstunde). Der Kreismittelpunkt wäre nicht Nodus für die Anzeige des mittleren Zeitpunktes mit Hilfe einer fiktiven mittleren Sonne. Die entsprechende Strich-Punkt-Linie verfehlt in der Regel den Schnittpunkt der beiden von der realen Sonne erzeugten Schattenlinien (s. 5:1- und 10:1-Vergrößerungen). Deshalb sind die Stundenlinien geringfügig verdreht und ungerade, sie haben prinzipiell die gleiche Form und Verdrehung wie die rote Mittellinie im Zeitgleichungs-Analemma von Abb.3 im Vergleich zur vertikalen Zeitgleichungs-Null-Linie.

Beim Gebrauch der Hollander-Uhr wird viermal im Jahr zwischen dem Ablesen auf dem voreilenden und auf dem nacheilenden Kantenschatten analog zum Vorzeichenwechsel der Zeitgleichung gewechselt. In folgenden Teilen des Jahres werden folgende Kantenschatten gebraucht [1]:
22.Dezember bis 12.April: voreilender Kantenschatten,
12.April bis 20.Juni: nacheilender Kantenschatten,
20.Juni bis 30. August: voreilender Kantenschatten,
30.August bis 20.Dezember: nacheilender Kantenschatten (Anmerkung 5).

Aus den Abbildungen 7 und 8 ist erkennbar bzw. ableitbar, dass die Anzeige der Hollander-Uhr im Vergleich zur einfachen ebenen Horizontaluhr mit Nodus im Allgemeinen gegen Süd verschoben ist, und, dass die Verschiebung bei der Anzeige der Randstunden des Tages wegen des Gebrauchs eines immer größeren und südlicheren Nodus-Kreises progressiv wächst. Die Datenlinien sind also nicht nur gegen Süden verschoben, sondern sie sind auch zusätzlich gegen Süden gekrümmt. Die sommerlichen Datenlinien sind gegenüber den "einfachen" Hyperbeln stärker gekrümmt. Anstatt der "einfachen Gerade" an den Tagen der Tag-Nacht-Gleichen gibt es eine schwach gegen Süd gekrümmte Linie. Die restlichen, winterlichen Linien sind schächer gegen Norden gekrümmt als die "einfachen" Vergleichshyperbeln. An den Tagen der Sonnenwenden bleibt es bei den unveränderten "einfachen" Hyperbeln, weil der Nodus nicht von der Kegelspitze weg gewandert ist.

Die allgemeine Verschiebung der Tageslinien gegen Süd hat eine Linien-Verdünnung in der Nachbarschaft der Linie für die Wintersonnenwende zur Folge. In der Nachbarschaft der Linie für die Sommersonnenwende kommt es zu einer Verdichtung und sogar zu einer Überschreitung von Linien untereinander [3]: Anstatt der Sonnenwend-Parabel ist etwa die Linie für δ=23° die südlichste Linie (Anmerkung 6).

5. Hollander-Sonnenuhr mit Doppelkegel  ↑

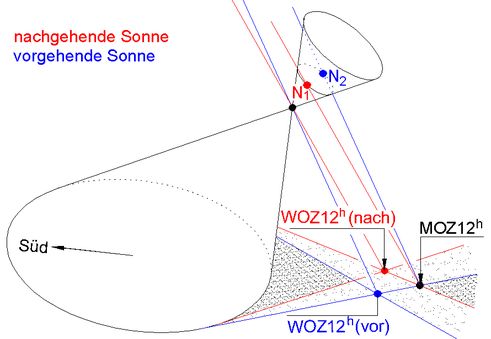
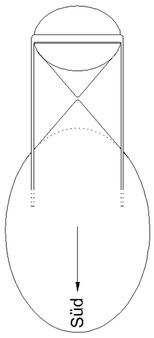Abb.10 Hollander-Sonnenuhr
           mit erdachsparallelem Doppelkegel als Schattenwerfer
           Dargestellt ist die Anzeige der Mittagsstunde mit dem aufgesetzen Kegelteil,
           der mittels eines Bügels am Hauptkegel befestigt ist (rechtes Teilbild).

Die in Abb.10 vorgeschlagene Variante der Hollander-Uhr mit Doppelkegel als Schattenwerfer hat nicht den Nachteil, dass sich die Datenlinien in der Nachbarschaft der Sommensonnenwende gegenseitig überschreiten. Im Zeitraum vom 13.April bis zum 30.August wird nämlich der aufgesetzte Kegelteil zur Zeitanzeige benutzt. Die Datenlinien sind wie die im übrigen Zeitraum des Jahres von der anderen Seite her gegen die Datumslinie 12.April/30.August verschoben. Eine Überschreitung von Tageslinien kommt in der Nachbarschaft dieser Linie nicht vor, denn die Breite des Analemmas (Abb.3) ändert sich an der Analemma-Kreuzung mit wesentlich niedrigerem und endlich bleibenden Gradienten als am Analemma-"Fuß" und am -"Kopf" (dort jeweils gegen unendlich groß wachsend).

Der Terminkalender für den viermaligen Wechsel beim Ablesen der Uhr ändert sich nicht. Es ist lediglich der Wechsel zwischen den beiden Teilen des Doppelkegels am 13.April und am 30.August zu beachten.

Die Arme des Befestigungsbügels für den Kegelvorsatz liegen in der Stundenebene τ=-90°/+90° (Abb.10, rechtes Teilbild). Sie sind keine störemden Schattenwerfer, denn die Anzeige ist auf weniger als 12 Tagesstunden beschränkt
(s. Abb.2).

6. Literatur   ↑

7. Anmerkungen   ↑

Anmerkung 1:   ↑
Um die Zeit der Sonnenwenden funktioniert das angewendete Prinzip während einiger Tage nicht, weshalb die beiden Walzen oben und unten etwas gekürzt ausgeführt sind. Bei konvexer Walzenkontur könnte das Sonnenlicht nicht die |δ|=23,5° entsprechende Endpartie erreichen. Bei konkaver Kontur würde die überstehende ringförmige Endpartie an Tagen mit |δ| etwas kleiner als 23,5° einen Teil der entsprechenden Walzenoberfläche abschatten.

Anmerkung 2:   ↑
Der Nodus ist nach dem Mittag von Stunde zu Stunde lediglich immer weiter von der Kegelachse entfernt bereit zu stellen. Dass er zu jeder folgenden Stunde Punkt eines immer größeren Kreises ist, wäre bedeutungslos, so lange nur eine von zwei Mantellinien als Schattenkante gebraucht würde. Die wesentliche Besonderheit der Hollander-Uhr ist aber, dass die andere Mantellinie am Partnertag im Jahr (Tag mit gleicher Sonnendeklination) zur Anzeige auf denselben Stundenpunkten des Zifferblattes verwendet wird. Dafür ist die Kreis-Symmetrie am Schattenwerfer erforderlich.

Anmerkung 3:   ↑
Die in Abb.9 und im weiteren Text den δ- und ZG-Werten beigefügten Kalendertage gelten für das Jahr 2011. Im Allgemeinen verursacht der Schaltjahr-Rhythmus des Kalenders eine Abweichung bis zu einen Kalendertag.

Anmerkung 4:   ↑
Die Zeitgleichung ist zwar nicht null, hat aber für beide Partnertage den gleichen Wert. Die benachbarten Tage mit Zeitgleichung=null können nicht von der Kegelspitze angezeigt werden, denn ihr jeweiliger Partnertag hat einen kleinen endlichen Wert für die Zeitgleichung.

Anmerkung 5:   ↑
Wieland [3] setzt die Wechseltage auf 22.Dezember, 12.April, 21.Juni und 31.August. Meine Überlegungen führen zu 22.Dezember (Wintersonnenwende), 21.Juni (Sommersonnenwende), 13.April und 30.August. Die beiden letzteren Tage haben denselben und mittleren δ-Wert bezogen auf die Tage mit Zeitgleichung=null (15.April und 1.September). Siehe auch Anmerkung 3.

Anmerkung 6:   ↑
Der genaue Wert ist vom Spitzenwinkel des anzeigenden Kegels abhängig.