|
<< Home Sonnenuhr und Kegelschnitte(DGC-Mitteilungen Nr.106, 2006: "Jede Deklinationslinie der Sonnenuhr ist ein Stück eines echten Kegelschnittes") Bemerkung von 2008Im ursprünglichen Aufsatz von 2006 machte ich auf Fehler in einer einschlägigen Arbeit [1] aufmerksam. Die folgende Fassung ist allgemeiner und umfassender gehalten.ZusammenfassungDie von einem Punkt-förmigen Schattenwerfer herrührende Tagesspur auf einer Sonnenuhr kennzeichnet die Jahreszeit. Man nennt sie Datums- oder Deklinationslinie, letzteres, weil sie eine Funktion der Sonnen-Deklination δ ist. Die Linien haben die Form von Kegelschnitten. Es wird gezeigt, welche Linienarten beim Schneiden eines Kegels entstehen und von welcher Art jede einzelne Linie auf einem ebenen Zifferblatt in Abhängigkeit von der Deklination δ, der geographischen Breite φ und der Zifferblatt-Lage (insbesondere vertikal oder horizontal) ist.Inhalt1. Einleitung2. Kegelschnitte 3. Kreiskegel aus Sonnen- und Schattenstrahlen, ebene vertikale Sonnenuhr 4. Für welche geografische Breite ist die vertikale Sonnenuhr geeignet? 5. Kreiskegel aus Sonnen- und Schattenstrahlen, ebene horizontale Sonnenuhr 6. Zusammenfassung: Welche Kegelschnitte wo und wann ? 7. Literatur (inkl. Bildnachweis) 1. Einleitung ↑ AnfangBei einer Sonnenuhr mit anzeigendem Schatten-Punkt ist ausser der Tages- auch die Jahreszeit (Jahres-Datum) abzulesen. Die Tagesbahn des Punktes ist nämlich täglich eine andere und hat die geometrische Form eines Kegelschnittes. Zu untersuchen ist, welche/r Kegelschnitt/e wann und wo vorlieg/t/en. 2. Kegelschnitte ↑ AnfangIch beginne ausnahmsweise mit einem mathematischen Kapitel, mit dem über Kegelschnitte, und zitiere aus einem Taschenbuch für Ingenieure [2]:
"Räumlich ergeben sich die Kegelschnitte als Schnittkurven einer geraden Ebene und eines Kreiskegels .. ." (Abb.1) ".. Hiernach erhält man eine Ellipse, Parabel oder Hyperbel, je nachdem die schneidende Ebene zu keiner Mantellinie parallel ist (Ebene II), zu einer Mantellinie (Ebene III) oder zu zwei Mantellinien parallel ist (Ebene IV). Ist die Ebene senkrecht zur Kegelachse (Ebene I), so entsteht ein Kreis als Sonderfall von II." 3. Kreiskegel aus Sonnen- und Schattenstrahlen, ebene vertikale Sonnenuhr ↑ AnfangDer Schatten-werfende Punkt einer Sonnenuhr ist die Spitze des Doppel-Kreiskegels von Abb.1, die Himmelsachse zwischen Himmels-Süd- und -Nordpol ist die Kegelachse. Der in Abb.2 gezeigte Kreiskegel aus Sonnen- und Schattenstrahlen ist wesentlich stumpfer als der von Abb.1. Dabei ist sogar eine spitzeste Form, nämlich die, die zur Winter-Sonnenwende (δ = -23,44°) gilt, gezeichnet. Die Sonnenstrahlen bilden zu dieser Zeit den linken, die Schattenstrahlen den rechten Kegel. Zur Tag/Nacht-Gleiche (δ =0) sind die Kegel zu einer Ebene, die den Himmels-Äquator enthält, degeneriert. Im Sommer-Halbjahr sind Licht- und Schatten-Kegel gegeneinander vertauscht. Die Sonne ist rechts (δ > 0).
Zwischenbemerkung: Abb.2 enthält die gleichen Schnittflächen I bis IV wie Abb.1 und extra die Flächen IV.1 und IV.2. Setzt man die Flächen vertikalen Sonnenuhren-Zifferblättern auf Südwänden gleich, dann ist I eine Sonnenuhr am Äquator (φ =0), III eine am nördlichen Wendekreis (φ = +23,44°), IV.1 eine am Polarkreis (φ = +66,56°) und IV.2 eine am Nordpol (φ = 90°). Am häufigsten ist Fall IV. Er gilt nördlich des Wendekreises. Also sind überall in Europa alle Deklinationslinien auf vertikalen Sonnenuhren nur Hyperbeln. (Abb.3). Die Abbildungen 3 bis 6 enthalten die wesentlichsten Fälle von Zifferblättern vertikaler Sonnenuhren (Süduhren). Schatten-werfender Punkt ist die Spitze eines horizontalen Stabes (Gnomon), der nach oben geklappt gezeichnet ist. Am Äquator (Fall I , φ = 0) gibt es nur Kreise (Abb.3), und die Südwand ist nur im Winter (δ < 0) beleuchtet. Der Kreis für die Tag/Nacht-Gleiche (δ = 0) ist wegen Streiflicht unendlich gross.
Nördlich davon bis φ = +23,44° sind es Ellipsen (Fall II), eine Parabel (III, am Tage -δ = φ) und Hyperbeln (IV): Abb.4. Zur Tag/Nacht-Gleiche (δ = 0) wird die Hyperbel zur Äquinoktial-Gerade. Am Tag +δ = φ tritt die Südwand in den Schatten.
Abb.5 zeigt das bei uns "heimische" Zifferblatt einer Süduhr.
Am Nordpol (φ = 90°) scheint die Sonne nur im Sommerhalbjahr, dafür ganztätig. Die Wandorientierung ist beliebig, aber jede Wand ist den halben Tag lang im Schatten (was wohl niemand ernsthaft interessieren dürfte, Abb.6).
4. Für welche geografische Breite ist die vertikale Sonnenuhr geeignet? ↑ AnfangIn der Nähe und innerhalb der Wendekreise sind vertikale Sonnenuhren aus folgenden Gründen wenig geeignet:
In der Nähe und jenseits der Polarkreise
Ausser in mittleren geographischen Breiten ist die horizontale die Standard-Sonnenuhr.
Die von mir fotografierte Äquator-nächste vertikale Sonnenuhr befindet sich in Cordoba/Argentinien (Abb.7, φ ≈ -32°). Man beachte den langen Schatten. Sie ist ohne Datumslinien. Eine solche Linie, die z.B. vom Ende der Polkante aufgezeichnet würde, läge zur Zeit der Aufnahme (19.Okt.) unterhalb der Zifferblatt-Tafel. 5. Kreiskegel aus Sonnen- und Schattenstrahlen, ebene horizontale Sonnenuhr ↑ Anfang
Abb.8 ist für horizontale Sonnenuhren gezeichnet und ist fast gleich wie Abb.2. Die Himmelsachse ist umgekehrt. Die links stehende Sonne scheint zur Sommersonnenwende (δ = +23,44°). Die Schnittflächen gehören zu geografischen Breiten, die zu den bisherigen Werten komplementär sind (90°-φ): Am häufigsten ist wie bereits schon bei den vertikalen Sonnenuhren der Fall IV. Alle horizontalen Sonnenuhren südlich des Polarkreises haben als Datumslinien nur Hyperbeln.
Was bei der vertikalen Uhr in Äquatornähe gilt, stimmt bei der horizontalen Sonnenuhr in Polnähe und umgekehrt. Einzige Besonderheit bei der horizontalen Uhr ist die nicht fehlende Besonnung in Äquatornähe, weil bei ihr die Besonnung niemals auf die Rückseite wechselt. Die den Abbildungen 3 bis 6 entsprechenden Zifferblätter kann man sich leicht vorstellen oder mit Hilfe des auch von mir verwendeten Computerprogramms [3] selbst anfertigen. Ellipsen, eine Parabel und Hyperbeln kommen gemeinsam nur nördlich des Polarkreises vor. Ein solches Zifferblatt ist beigefügt (Abb.9), denn auf ihm sind (im Gegensatz zu Abb.4) einige Datumslinien vollständige Ellipsen. Der (vertikale, nach Nord geklappt gezeichnete) Gnomon ist nur 1/3 so lang wie in Abb.4.
Zum Schluss noch ein Bild eines "handgemachten" horizontalen Kegelschnittes: Abb.10. 6. Zusammenfassung: Welche Kegelschnitte wo und wann ? ↑ AnfangIn den Diagrammen der Abb.11 sind die Vorkommen der verschiedenen Kegelschnitte in Abhängigkeit von der Deklination und der geographischen Breite dargestellt. Das rechte Diagramm fasst das für die vertikale Sonnenuhr Gesagte zusammen (Abschnitt 3). Im linken Diagramm sind die Verhältnisse bei der horizontalen Sonnenuhr, der anderen Sonderlage ebener Zifferblätter, gezeigt (Abschnitt 5.).
7. Literatur (inkl. Bildnachweis) ↑ Anfang
[1] O.Feustel: "Jede Deklinationslinie der Sonnenuhr ein Kegelschnitt", DGC-Jahresschrift 2005 ↑↑ Anfang |
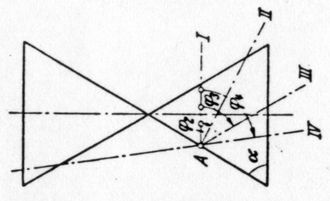 <<
Abb.1 Kegelschnitte [2]
<<
Abb.1 Kegelschnitte [2]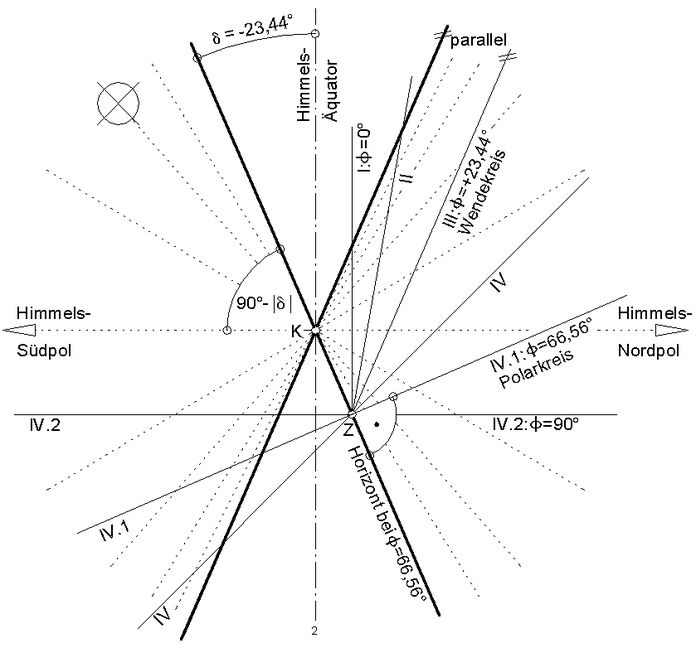 Abb.2 Kegelschnitte auf vertikalen Süd-Sonnenuhren,
nördliche geographische Breiten (φ = 0 bis 90°)
Abb.2 Kegelschnitte auf vertikalen Süd-Sonnenuhren,
nördliche geographische Breiten (φ = 0 bis 90°) 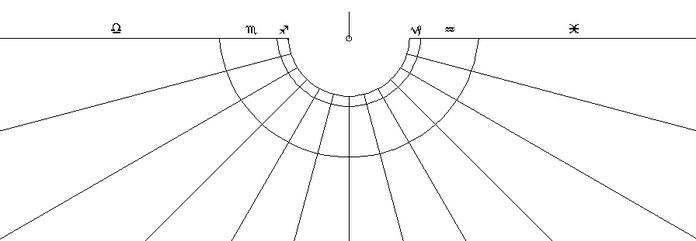 Abb.3 Deklinationslinien auf einer Süduhr am Äquator
Abb.3 Deklinationslinien auf einer Süduhr am Äquator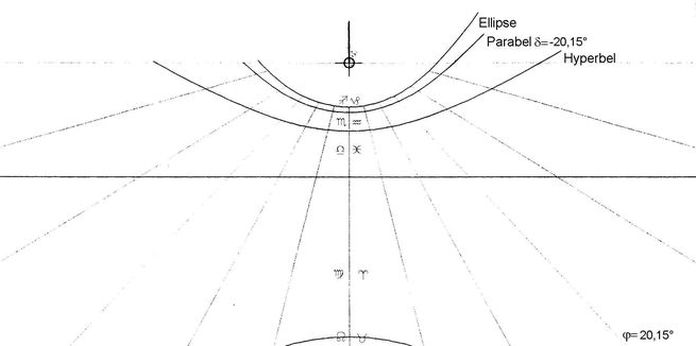 Abb.4 Deklinationslinien auf einer Süduhr bei φ=20.15°
Abb.4 Deklinationslinien auf einer Süduhr bei φ=20.15°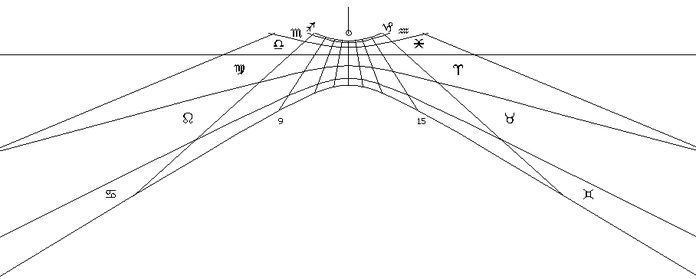 Abb.5 Deklinationslinien auf einer Süduhr bei φ=+50°
Abb.5 Deklinationslinien auf einer Süduhr bei φ=+50°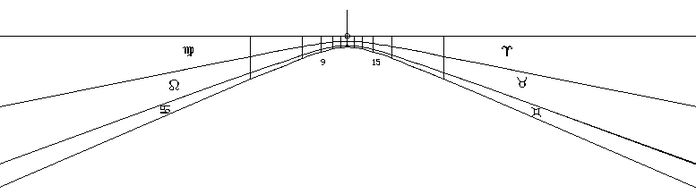 Abb.6 Deklinationslinien auf einer Wanduhr am Nordpol
Abb.6 Deklinationslinien auf einer Wanduhr am Nordpol <<
Abb.7 Vertikale Nordwand-Sonnenuhr in Cordoba /Arg., φ ≈ -32°
<<
Abb.7 Vertikale Nordwand-Sonnenuhr in Cordoba /Arg., φ ≈ -32°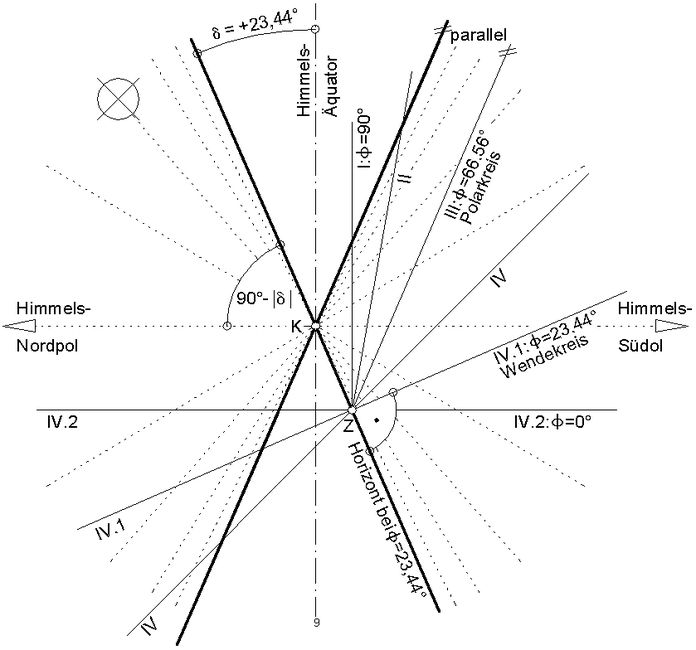 Abb.8 Kegelschnitte auf horizontalen Sonnenuhren,
nördliche geographische Breiten (φ = 0 bis 90°)
Abb.8 Kegelschnitte auf horizontalen Sonnenuhren,
nördliche geographische Breiten (φ = 0 bis 90°) 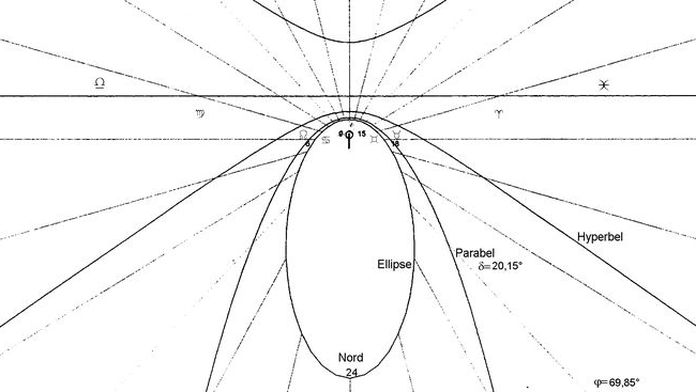 Abb.9 Deklinationslinien auf einer horizontalen Sonnenuhr bei φ=69,85°
Abb.9 Deklinationslinien auf einer horizontalen Sonnenuhr bei φ=69,85° <<
Abb.10 Tagesspur im Sand einer Südseeinsel
<<
Abb.10 Tagesspur im Sand einer Südseeinsel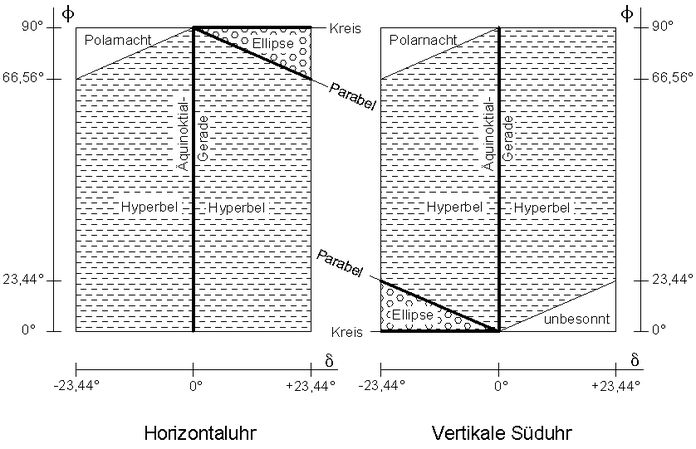 Abb.11 Art des Kegelschnittes, abhängig von Deklination δ und Breite φ
Abb.11 Art des Kegelschnittes, abhängig von Deklination δ und Breite φ