<< Home
<< andere Sonnenuhren-Beiträge
↓↓ Ende
Schatten von Gebäuden und hohen Sonnenuhren
Überarbeitung eines anlässlich der Jahrestagung des Arbeitskreises Sonnenuhren in der Deutschen Gesellschaft für Chronologie gehaltenen Vortrags (Heppenheim, 10. Mai 2013)

Zusammenfassung
Der von Gebäuden und Bäumen geworfene Schatten ist in einer Wohnsiedlung nicht beliebt, vor allem dann, wenn sich ein solcher Schattenwerfer auf dem Grundstück des Nachbars befindet. Ist ein neues Haus nebenan erst geplant, so möchte man dessen Schatten und seine tägliche und jährliche Änderung im Voraus kennen, um allenfalls gegen den Neubau Einspruch zu erheben. Der Architekt des Neubaus besitzt in der Regel ein PC-Programm, mit dem er die entsprechende Simultion konfortabel vornehmen kann. Die von den Sonnenuhrenfreunden benutzten PC-Programme erfüllen grundsätzlich dieselbe Aufgabe, die nur umgekehrt zu formulieren ist: Wohin fällt der Schatten eines Schattenwerfers zu einem bestimmten Zeitpunkt? (anstatt: Welche Zeit ist es, wenn der Schatten an eine bestimmte Stelle fällt?) Ich zeige, dass mit einem solchen Rechenprogramm der Schatten eines Hauses auf eine ebene Fläche (eine Gartenfläche) zwar nicht als Animation dargestellt, aber eine oft ausreichende, schrittweise vorgenommene Vorhersage gemacht werden kann. Abb.1 Le Corbusier : Hochhaus und Sonne >>>Der kleine Bund, Bern, 8. April 2013
Vom Architekten Le Corbusier stammen einige bemerkenswerte Hochhäuser. In einer von ihm angefertigten Zeichnung (Abb.1) scheint er den von diesen Häusern geworfenen Schatten irgendwie aus der Welt schaffen zu wollen, indem er die Sonne unrealistischerweise in den Vordergrund stellt.
Ein Gebäude-Schatten kann lästig sein unabhängig davon, dass sein Rand von oberen Gebäudeteilen nicht scharf begrenzt ist. Anlässlich seiner Ermittlung mit einem Sonnenuhren-Rechenprogramm möchte ich daran erinnern, dass Sonnenuhren in ähnlicher Größe wegen der Schattenrandunschärfe nicht ablesbar sind. Jüngste Missachtung dieser Erfahrung ereignete sich in Kalifornien, wo man den etwa 60 Meter hohen und nach Norden geneigten Pfeiler einer Brücke zusätzlich zu einen Sonnenuhren-Schattenwerfer machte und die sogenannte Sundial Bridge zur (äüßerst schlecht funktionierenden) größten Sonnenuhr der Welt erklärte.
Ein mit einem Sonnenuhren-Entwurfsprogramm ermittelter Hauschatten
Ich verwendete das von unserem Sonnenuhrenfreund Helmut Sonderegger angefertigte Programm Sonne. In Bezug auf die von einer Hamburger Hausbesitzerin gestellten Frage nach dem von einem auf dem Nachbargrundstück geplanten Haus zu erwartenden Schatten in ihrem Garten entwarf ich damit ein horizontales Sonnenuhren-Zifferblatt für die geographische Breite von 53,5° in Hamburg (Abb.2). Der Maßstab ergibt sich aus der Höhe von 6,5 Meter des geplanten Hauses mit Flachdach. In dieser Höhe befindet sich der punktförmige Schattenwerfer (Spitze eines auf dem kleinen Kreis auf der Mittagslinie 12|12 stehenden Gnomons). Auf die radialen Strahlen fällt der Schatten zu bestimmeten Stunden des Tages, auf die quer dazu verlaufenden Hyperbeln an bestimmten Tagen im Jahr. Die Stundenlinien markieren die sogenannte wahre Ortszeit (WOZ). Zur Umrechnung in Mitteleuropäische Zeit sind in Hamburg (geographische Länge = 10° Ost) 20 Minuten zu addieren (im Sommer 1 Stunde und 20 Minuten). Die übers Jahr schwankende Sonnenzeit gegenüber der gleichmäßig vergehenden amtlichen Zeit von bis zu etwa ± 15 Minuten im Winterhalbjahr (Stichwort: Zeitgleichung) wäre noch zusätzlich zu beachten.
Der direkte Gebrauch des Programms Sonne endete mit dem erstellten Zifferblatt, das ich in den weiteren Schritten mit einem CAD-Programm (AutoCAD) behandelte.
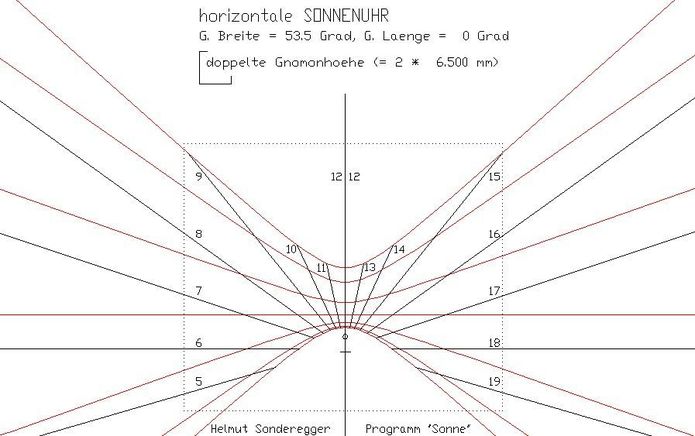 Abb.2 Zifferblatt einer Horizontalen Sonnenuhr für geographische Breite 53,5°, Anzeige: 5 bis 19 Uhr wahre Ortszeit
Abb.2 Zifferblatt einer Horizontalen Sonnenuhr für geographische Breite 53,5°, Anzeige: 5 bis 19 Uhr wahre Ortszeit
(Die früheren und späteren Sommer-Sonnenstunden sind weggelassen.)
In Abb.3 ist nur der mit einem Rahmen in Abb.2 gekennzeichnete innere Zifferblattteil übernommen worden. Schattenwerfer sind die oberen Ecken der Nordwand des 14 Meter breiten und 6,5 Meter hohen Flachdach-Hauses. Die beiden Hälften des symmetrischen Zifferblattes sind 14 Meter auseinander gezogen, jede Hälfte ist für die Ermittlung je eines Ecke-Schattens für je eine Tageshälfte benutzt worden. Das Schattenende ist eine zur Hauswand parallele Gerade, deren Verbindungsgeraden zu den Fußpunkten der Hausecken die Schattenfläche der Norwand vervollständigen. Die Schattenflächen der Hausseitenwände sind analoge Parallelogramme.
Die Schatten der Nordwand sind beispielsweise für einen Tag auf der Datumslinie für den Beginn der Sternzeichen Fische (etwa 20. Februar) und Scorpion (etwa 24. Oktober) zu jeder vollen Stunde gezeichnet. Beginn ist 8 Uhr, Ende ist 16 Uhr WOZ (die Sonne scheint an diesen Tagen in Hamburg unwesentlich länger). Schattenpunkt des oberen Endes einer Hausecke ist der Schnittpunkt der Stundenlinie mit der Datumsslinie.
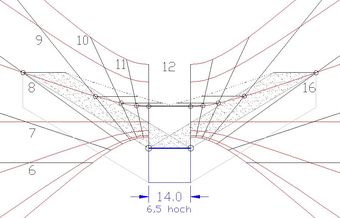
 ↑ ↑ Abb.3 Tageslauf des Schattens eines Hauses mit Flachdach, Haus südlich ausgerichtet
↑ ↑ Abb.3 Tageslauf des Schattens eines Hauses mit Flachdach, Haus südlich ausgerichtet
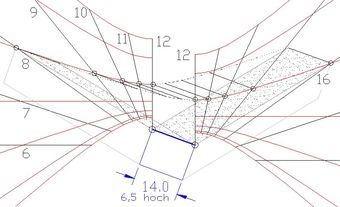
Abb.4 Tageslauf des Schattens eines Hauses mit Flachdach, Haus 30° verdreht (westabweichende Südwand) ↑ ↑
Wie vorzugehen ist, wenn das geplante Haus keine genaue Südwand haben sollte, zeigt Abb.4. Die Wand zur Sonnenseite ist beispielsweise 30° nach West verdreht. Die Hälften des Zifferblattes sind gemeinsm mit den Hausecken wie diese gegenseitig verschoben. Die Schattenflächen sind etwas andere Parallelogramme als bei Südausrichtung des Hauses. Die Situation ist nicht mehr symmetrisch zwischen Vor- und Nachmittag. Am Vormittag ist der Schatten der Nordwand schmaler als am Nachmittag. Dafür ist der Schatten der linken Wand am Vormittag etwas breiter als der der rechten Wand am Nachmittag.
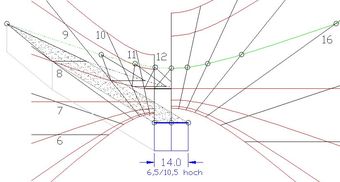 Abb.5 Tageslauf des Schattens eines Hauses mit Satteldach, Süd-Nord-Fist
Abb.5 Tageslauf des Schattens eines Hauses mit Satteldach, Süd-Nord-Fist
Eine Vorschau des Schattens für den Fall, dass das Haus mit einem Satteldach mit Süd-Nord-Fist nach oben erweitert werden sollte, ist mit Hilfe der Abb. 5 zu gewinnen. Für die Spitze des Schatten-verlängernden Dreiecks wird ein zweites Sonnenuhren-Zifferblatt mit Gnomonhöhe von beispielsweise 10,5 Metern benötigt. Von diesem Zifferblatt ist zur Wahrung der Übersicht diesmal nur die rechte Hälfte gezeichnet. Nur die stündlichen Schattenpunkte an den betrachteten zwei Tagen im Jahr sind links eingezeichnet (wegen Symmetrie durch Spiegeln um die Mittagslinie 12|12 gewonnen). Mit der aus Abb.3 übernommenen Basis des Dreieck-Schattens ließ sich dieses komplettieren. Der nachmittägliche Schattenverlauf ergibt sich durch Spiegelung des vormittäglichen um die Mittagslinie 12|12.
Die Schatten der in den Beispielen behandelnden Hausformen lassen sich lediglich mit den Schatten von zwei Punkten an der Hülle des Hauses ermitteln. Weniger einfache Hausformen lassen sich gleich einfach behandeln, nur der Aufwand infolge des Arbeitens mit mehreren Punkten ist größer.
Der unscharfe Schatten auf einer Sonnenuhr mit zu hohem Schattenwerfer
Die erschwerte Ablesegenauigkeit infolge eines unscharfen Schattens besteht nur bei Sonnenuhren mit punktförmigem Schattenwerfer (Nodus). Der Schatten ist umso weniger scharf, je weiter weg er von seinem Erzeuger bei einer solchen Sonnenuhr in den frühen und späten Tagesstunden und im Winterhalbjahr fällt. Sonnenuhren mit Polstab sind diesbezüglich von Vorteil. Der Schatten dieses Stabes reicht in den genannten Zeiten zwar ebenfalls sehr weit. Man kann aber jeden Teil seines Schattens zur Anzeige gebrauchen, also in den problematischen Zeiten denjenigen wenig weit entfernten Teil ablesen, der vom nahe beim Fußpunkt befindlichen Stabteil erzeugt ist. Unabhängig von der wegen Unschärfe des Schattens begrenzten Anwendungsmöglichkeit einer Nodus-Sonnenuhr ist das Zifferblatt einer Polstab-Sonnenuhr immer wesentlich kleiner als bei ersterer (siehe auch Sonnenuhr und Mathematik, vorletzter Absatz). Es wird in der Regel wesentlich kleiner ausgeführt als der aus anderen Gründen in Abb.2 angegebene innerere Ausschnitt. Das entsprechende Zifferblatt enthält nur die beim oder nahe beim Fußpunkt des Polstabs (Querstrich auf der Mittagslinie 12|12 unter dem kleinen Kreis für den Gnomonfußpunkt) beginnenden radialen Stundenlinien. Die Polstab-Sonnenuhr ist zeitlich sehr nahe bei Sonnenauf- und Untergang ablesbar, während ein (kaum erkennbarer) Punktschatten noch beziehungsweis schon jenseits eines praktisch ausgeführten Zifferblattes liegt.
Ein Schatten-werfender Punkt ist in der materiellen Praxis in einfachster Weise eine Kugel. Der im Sonnenlicht hinter ihr enstehende Schatten wird mit wachsender Entfernung der Auffangfläche unscharf und verschwindet bei größerer Entfernung. Die Sonne ist keine kleine punktförmige Lichtquelle, sondern wird in einem Winkel von etwa 2σ = 0,53° zwischen ihren gegenüber liegenden Kreisrändern gesehen. Der Kernschatten hinter einer Kugel mit Radius R hat seine Spitze in einer Entfernung von e = R / sinσ (Abb.6), er reicht also nicht beliebig weit. Die Reichweite ist in Wirklichkeit noch kleiner, weil das Sonnenlicht am Kugelrand nicht in idealerweise Weise abgeschnitten wird, sondern weil zusätzlich Licht in den Kernschatten hinein gebeugt und von Teilchen in der Luft hinein gestreut wird. Der nach dem Verschwinden des Kernschattens verbleibende Halbschatten ist als Sonnenuhren-Zeiger zu schwach und verschwindet zudem stetig nach außen.
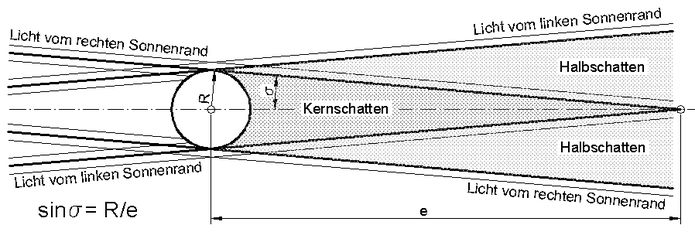 Abb.6 Reichweite des Kernschatten-Kegels hinter einer Kugel
Abb.6 Reichweite des Kernschatten-Kegels hinter einer Kugel
Dass eine Nodus-Sonnenuhr nicht beliebig groß sein kann, wurde anlässlich der in den 1970er Jahren rekonstruierten angeblichen Sonnenuhr des Augustus (Abb.7) in den Vordergrund gerückt [1]. Es wurde gezeigt, dass der Schatten einer in 30 m Höhe befindlichen 74 cm großen Kugel nicht einmal auf der Linie der vierten Stunde (damals temporäre Stunden) vor und nach Mittag vorhanden ist. Diese Überlegung führte zur Rückdeutung der Sonnenuhr des Augustus auf den Meridian des Augustus (Schattenwurf nur auf und Ablesung nur von der Mittagslinie).
 Abb.7 angebliche Sonnenuhr des Römischen Kaisers Augustus, Schatten der Kugel wesentlich zu groß gezeichnet,
Abb.7 angebliche Sonnenuhr des Römischen Kaisers Augustus, Schatten der Kugel wesentlich zu groß gezeichnet,
da zu dieser Zeit kurz vor dem Verschwinden, Bildnachweis in Sonnenuhr und Mathematik

 ↑ ↑ Abb.8 Der Gnomon des Meridian des Augustus, heute vor dem italienischen Parlamentsgebäude,
↑ ↑ Abb.8 Der Gnomon des Meridian des Augustus, heute vor dem italienischen Parlamentsgebäude,
Abb.9 Sonnenuhr mit Kugel-Nodus auf der Halde Hoheward bei Recklinghausen ↑ ↑
Wikimedia Commons: File:Obelisk of montecitorio arp.jpg und File:Haldenpanorama 009.jpg
In jüngster Zeit wurde erneut eine größte Sonnenuhr der Welt kreiert. Anlass war der annähernd im gleichen Winkel wie ein Polstab nach Norden geneigte Pfeiler einer modernen vom Spanier Architekt Santiago Calatrava entworfenen Schrägseil-Brücke für Fußgänger in Kalifornien (Abb.10). Sie wurde zur Ankurbelung des Tourismus Sundial Bridge getauft und ihr Pfeiler zusätzlich zum Schattenwerfer einer Sonnenuhr gemacht. Um ins Guinnessbuch der Rekorde zu passen, wird der Brückenpfeiler (oder eine seiner Kanten) folgerichtig nicht als Polstab (oder als Polkante) sondern dessen Spitze als Nodus benutzt. Die Einschränkung auf eine Sonnenuhr, die nur kurze Zeit im Jahr benutzbar ist, steht im Kleingedruckten auf den Stundenmarken am Boden (Abb.11). Man hat nämlich nur ein paar dieser Marken auf eine Tageslinie (kurzer weißer Bogen in Abb.10) der Sommersonnenwende gesetzt, auf die wegen der Steilheit der Sonne an diesem Tag ein einigermaßen scharfer Schatten der etwa 60m hohen Pfeilerspitze fällt.
Nebenbemerkung: Die Neigung des Pfeilers ist gegenüber der richtigen Neigung eines Polstabs etwa 8° zu klein (Abb.12), so dass die bescheidenere Nutzung des vorwiegend unteren Teils des Pfeilers für eine Polstab-Sonnenuhr ausscheidet.

 ↑ ↑ Abb.10 Schrägseilbrücke (Sundial bridge) in Redding/Kalifornien mit geneigtem Pfeiler, Blick gegen Westen
↑ ↑ Abb.10 Schrägseilbrücke (Sundial bridge) in Redding/Kalifornien mit geneigtem Pfeiler, Blick gegen Westen
Abb.11 eine Stundenmarke der Sonnenuhr an der Sundial bridge ↑ ↑
http://en.wikipedia.org/wiki/File:Sundial_Bridge_time_marker_noon.jpg
 Abb.12 Sundial bridge: Pfeilerwinkel gegen Boden 49° anstatt für einen Postab erforderliche 40,6°
Abb.12 Sundial bridge: Pfeilerwinkel gegen Boden 49° anstatt für einen Postab erforderliche 40,6°
(= geographische Breite von Redding/Kalifornien),
steile Mittagssonne zur Sommersonnenwende (17,1° weniger als aus dem Zenit),
Blick gegen Osten.
http://www.usatipps.com/Webalbum/NordwestenUSASommer2012/018_Sundial_Bridge/slides/04.html