<< Home
<< andere Sonnenuhren-Beiträge
↓↓ Ende
Zum Nachdenken 2: Gleichzeitiger Sonnenaufgang in Hamburg und Wien
Rundschreiben Nr.54 der Arbeitsgruppe Sonnenuhren im Österreichischen Astronomischen Verein, Dezember 2017Inhalt
1. Einleitung2. Aufgabe
3. Vorüberlegungen
3.1 Scheinbarer Sonnenaufgang
3.2 Eine zum Rechnen verwendbare Grundgleichung
4. Lösung
5. Weitere Überlegungen
5.1 Genaueres zu Abschnitt 4. Lösung
5.2 Warum ist die Sonnendeklination bei Sonnenaufgang an den gefundenen zwei Tagen nicht gleich?
5.3 Bedeutung der gegraphischen Längen von Hamburg und Wien
5.4 Berechnung von δgenau
5.5 An welchen Orten ist der Sonnenaufgang genau gleichzeitig?
5.6 Wie groß ist der kleine Unterschied zwischen den Sonnenaufgangszeiten in Hamburg und Wien?
5.7 Welche wären die genauen Sonnenaufgangszeiten in Hamburg bzw. in Wien?
6. Erkenntnis
7. Verweise
8. Zusatzaufgabe
1. Einleitung ↑ Anfang
Obwohl Hamburg westlicher als Wien liegt, kann in beiden Städten die Sonne im Sommer an zwei Kalendertagen etwa zur gleichen Zeit aufgehen. Ursache ist der umso längere lichte Sommertag, je größer die geographische Breite (φ) ist. In dieser Hinsicht ist das nördlicher als Wien gelegene Hamburg im Vorteil. In der Zeit um die Sommersonnenwende herum geht die Sonne in Hamburg sogar früher als in Wien auf. Wenige Wochen vorher und nachher beobachtet man in beiden Städten etwa gleichzeitigen Sonnenaufgang.
2. Aufgabe ↑ Anfang
Um welche/s Datum/en und zu welcher/n Uhrzeit/en ist das im Jahr 2017 der Fall? (auf Minuten gerundete Uhrzeit/en … ausreichend.)
3. Vorüberlegungen ↑ Anfang
3.1 Scheinbarer Sonnenaufgang ↑ Anfang
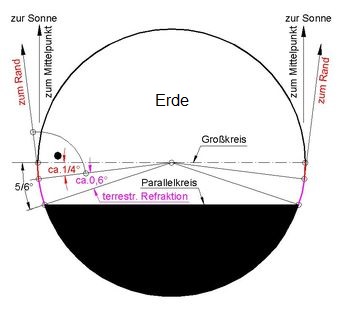
Bei mathematischem Sonnenaufgang ist der Höhenwinkel der Sonne h=0°. Der Mittelpunkt der Sonne liegt dann auf dem (mathematischen) Horizont. Üblicherweise wird bereits das Erscheinen des oberen Sonnenrandes als Moment des Sonnenaufgangs bezeichnet. Der Höhenwinkel des Sonnenmittelpunktes ist in diesem Moment h ≈ -¼° (Sonnendurchmesser
h ≈ ½°). Wegen der besonders in Bodennähe wirksamen Lichtkrümmung in der Atmosphäre (Folge der sogenannten terrestrischen Refraktion [2]), kann man etwa 0,6° über den "Tellerrand" hinaus nach unten schauen. Der i.d.R. verwendete Höhenwinkel im Moment, in dem der Sonnenrand am Horizont erscheint, ist die Summe aus beiden Werten:
h = - 0,833° (¼ ° + 0,6° ≈ - 5/6°).
Es handelt sich um den sogenannten scheinbaren Sonnenaufgang. Dieser ist im Folgenden immer gemeint, auch wenn das Adjektiv scheinbar weggelassen ist.
Nebenstehende Abbildung zeigt nicht- maßstäblich (zu groß gezeichnete Winkel), dass der Sonnenrand von der Erde aus schon von einem Punkt auf dem Parallelkreis (Terminator) aus sichtbar wird.
3.2 Eine zum Rechnen verwendbare Grundgleichung ↑ Anfang
Die in der Antwort zu nennenden Größen Deklinations- (δ, für das Datum) und Stundenwinkel (Τ, für die Uhrzeit) der Sonne sind beide in Abhängigkeit vom Höhenwinkel h und der geographischen Breite φ des Beobachtungsortes in folgender bekannten Gleichung für die Berechnung des Höhenwinkels eines Himmelskörpers aus seinen äquatorialen Koordinaten Deklinations- und Stundenwinkel enthalten [3]:
(1) sinh = sinφ sinδ - cosφ cosδ cosΤ (Zentrum beider Koordinatensysteme ist der Ort der Beobachtung).
Im Folgenden wird die Umstellung (2) angewendet:
(2) cosΤ = - (sinh - sinφ sinδ) / (cosφ cos δ) .
Zum Rechnen mit Gleichung (2) muss die Sonnendeklination δ als bekannte Größe vorliegen. Man kann für ein für die Lösung vermutet richtiges Datum den in veröffentlichten Tabellen [4] enthaltnen Deklinationswert für 12h benutzen. Da sich die grundsätzlich variable Deklination der Sonne über den nur einen Tag langen Berechnungszeitraum nur sehr wenig ändert (insbesondere nahe des Datums der Sonnenwende), ist eine gute Näherungsberechnung des Stundenwinkels τ damit möglich.
4. Lösung ↑ Anfang
Am Tag der Sommersonnenwende hat die Sonnendeklination ihren maximalen Wert
δmax= 23,44°. Ebenso ist die Stundenwinkel-Differenz ΔΤHW = ΤHamb - ΤWien maximal, nämlich ΔΤHW ≈ - 7,0°
(zwei Rechnungen mit Gleichung (2) und φHamb = 53,6°, φWien = 48,2°).
Die Deklination ist als Funktion der Zeit annähernd eine Sinus-Linie, was in grober Näherung auch für die Stundenwinkel-Differenz angenommen werden kann.
An den fraglichen Tagen gleichen scheinbaren Sonnenaufgangs in Hamburg und Wien vor bzw. nach der Sommersonnenwende ist die Stundenwinkel-Differenz ΔΤHW gleich der negativen Längengrad-Differenz ΔλHW .
ΔΤHW= - ΔλHW = - 6,3° ,
(ΔλHW = λHamb - λWien = 6,3°;
mit λHamb = -10,0° und λWien = -16,3°) .
Die Sonnendeklination bei ΔΤHW = - 6,3° ist in erster Näherung δ1.N = 21,1° (= 23,44°· 6,3 / 7,0).
Die entsprechenden annähernd passenden Kalendertage sind der 26. Mai und der 17. Juli 2017
(tabellierte Deklinationswerte 12h MEZ in [4]; 26. Mai: δ12h = 21,20°; 17. Juli: δ12h = 21,11°).
Die Rechnung wird mit diesen δ12h-Tabellenwerten und Gleichung (2) zweimal, bzw. für Hamburg und Wien getrennt durchgeführt. Anschließend wird die Differenz der ΔΤHW-Ergebnisse gebildet und mit dem Sollwert ΔΤHW = - 6,3° verglichen.
δ12h= 21,20° am 26. Mai 2017
ΤHamb = -123,53° WOZHamb = 03,76h WOZGörlitz = 04,10 h = 04:06
ΤWien = -117,21° WOZWien = 04,19h WOZGmünd = 04,10 h = 04:06 ΔΤHW= - 6,32° (anstatt -6,30° >>
Sonne geht in Hamburg etwa 5 Sekunden früher als in Wien auf : 0,02°·4min/° = 0,08 min = 4,8 sec)*).
MEZ = 04:03 (beachtete Zeitgleichung ZG ≈ +3 min; 12h- ZG-Wert [4])
δ12h = 21,11° am 17.Juli 2017
ΤHamb = -123,36° WOZHamb = 03,78h WOZGörlitz = 04,11 h = 04:07
ΤWien = -117,08° WOZWien = 04,19h WOZGmünd = 04,11 h = 04:07 ΔΤHW= - 6,28° (anstatt -6,30° >>
Sonne geht in Hamburg etwa 5 Sekunden später als in Wien auf : 0,02°·4min/° = 0,08 min = 4,8 sec)*).
MEZ = 04:13 (beachtete Zeitgleichung ZG ≈ -6 min; 12h- ZG-Wert [4]).
Diese bereits in grober Näherung gefundenen beiden**) Kalendertage sind die gesuchten.
Die Aufgabe ist somit schon gelöst.
*) Die Differenzen sind nur aufgeführt, um die zu erwartende Größenordnung zu zeigen, die sich hinter den in nur Minuten angegebenen Ergebnissen verbergen. Sie haben keine absolute Bedeutung, da sie aus Näherungsrechnungen mit Verwendung von δ12h-Werten (anstatt von tatsächlichen Werten bei Sonnenaufgang) stammen.
**) In den für die jeweils beiden benachbarten Kalendertage vorgenommennen Rechnungen weichen die Werte für ΔΤHW stärker vom Sollwert 6,3° als an den gefundenen Tagen ab. Dass der scheinbare Sonnenaufgang auch an diesen Kalendertagen noch auf die großzügig auf die jeweils nur in Minuten angegebene Uhrzeit fällt, ist sehr wahrscheinlich, wurde aber nicht untersucht.
5. Weitere Überlegungen ↑ Anfang
Weitere Überlegungen werden durch prinzipielle Ungereimtheiten, die wegen der relativ geringen Genauigkeitsansprüche vorerst in den Hintergrund gedrängt wurden, angeregt. Die Zusammenhänge werden erst deutlicher, wenn Zeitpunkte mit Sekundengenauigkeit angegeben werden, und wenn die geringe Änderung der Sonnendeklination über den Tag beachtet wird. Ihre Werte müssen dafür mit mehr als zwei Nachkommastellen berücksichtigt werden. Deshalb verwende ich wenigstens für die aus der Tabelle [4] (zwei Nachkommastellen) interpolierten Werte auch die dritte Nachkommstelle.
Anmerkungen:
Für qualitative Antworten (Vergleiche anstellen) mag diese "Überstrapazierung" der Tabellenwerte hinnehmbar sein. Bis zu einer eventuellen späteren Überarbeitung werde ich mir aber geauere Werte beschafft oder solche selbst ermittelt haben.
Die Aufgabenstellung präziziere ich dermassen, dass ich ab jetzt bei eventueller Ergebnisangabe in Minuten vorher übliches Runden vornehme, nicht - was die Aufgabenstellung auch hergibt - Minuten-Dezimalstellen oder Sekunden lediglich weglasse.
5.1 Genaueres zu Abschnitt 4. Lösung ↑ Anfang
Die Verwendung der Sonnendeklinations-Werte für 12h MEZ führt überhaupt nicht genau zu Sonnenaufgangszeiten in Hamburg und in Wien. Wenn nämlich am 15. Längengrad Ost bereits Mittag ist, dann geht die Sonne erst sehr viel weiter als in Hamburg und Wien im Westen auf.
Der Stundenwinkel der Sonne ist am 15. Längengrad etwa 0° (Meridiandurchgang), die Rechnungen mit Gleichung (2) ergeben Stundenwinkel von etwa τ = -120°. Daraus folgen Orte, an denen die Sonne gerade aufgeht, mit etwa +105° Längengrad (105° = -15° - (-120°)).
Eine genaue Betrachtung für Hamburger Breitengrad am 26. Mai: τ = -123,53°; Wahrer Mittag (τ = 0°) auf -14,25° Länge (Zeitgleichung = +3 min)
Gesuchter Längengrad = -14,25° - (-123,53°) = +109,28° .
Dieser genau bestimmte Ort befindet sich im Südwesten Kanadas (West-Saskatchewan).
Diese Betrachtung ändert nichts daran, dass hier die Sonne etwa 5 Sekunden früher aufgeht als am 6,3° östlicheren Ort in Kanada auf Wiener Breitengrad. Zum gleichzeitigen Sonnenaufgang an 6,3° in der Länge unterschiedlichen und die beiden vorgebebenen Breiten besitzenden Orten gehört offensichtlich ein anderer, ganz bestimmter Wert der Sonnendeklination. Er bestimmt aber nicht die absoluten Werte der geographischen Längen dieser beiden Orte (s. weiter unten.)
Die Überlegungen in den beiden folgenden Abschnitten werden zeigen, dass es präziser heißen muss: .... offensichtlich ein anderer, ganz bestimmter Wert der Sonnendeklination, der an den beiden Kalendertagen (26. Mai und 17. Juli) derselbe ist.
5.2 Warum ist die Sonnendeklination bei Sonnenaufgang
an den gefundenen zwei Tagen nicht gleich?
↑ Anfang
Nachdem im Abschnitt 4. Lösung Sonnenaufgangsuhrzeiten von etwa 04 h bestimmt wurden, werden die zu dieser Zeit bestehenden Deklinationswerte - nicht die zur obigen groben Näherungsrechnung benutzen Werte zu jeweils
12 h MEZ - betrachtet.
Lineare Interpolation der Tabellenwerte [4] für MEZ = 04 h ergibt:
δ = 21,143° am 26. Mai 2017 (21,165° zu 07 h MEZ) und
δ = 21,167° am 17. Juli 2017 (21,145° zu 07 h MEZ)
Dass beide Werte gleich sind, ist aus folgendem Grund prinzipiell nicht zwingend. Sie wären nur zufällig und näherungsweise gleich, wenn die Sommersonnenwende (δ ist maximal) am entsprechenden Junitag ebenfalls am Morgen zu etwa 4 h MEZ stattfände, denn die ungefähr sinusförmige δ(t)-Kurve verläuft annähernd symmetrisch beidseits dieses Maximum-Zeitpunktes. Im Jahr 2017 ist die Sommersonnenwende 5:24 MEZ, also nicht etwa 4 h MEZ, sondern deutlich später. Die Klammerwerte für 07 MEZ (etwa doppelt so viel später als die spätere Sonnenwende) bestätigen diese Symmetrie: im Überkreuz-Vergleich etwa gleiche Werte.
Es ist aber zwingend, dass die Sonnendeklination für genau gleichzeitigen Sonnenaufgang in Hamburg und Wien an beiden Tagen genau gleich sein müsste, egal ob sie langsam größer (im Mai) oder kleiner (im Juli) wird.
Weil das nicht zutrifft, ist der Sonnenaufgang in Hamburg und Wien nicht an beiden Tagen genau gleichzeitig. Er kann nur an einem dieser Tage genau oder annähernd gleichzeitig sein. Warum das so ist und an welchem der beiden Kalendertage bessere Gleichzeitigkeit besteht, folgt aus den nächsten Überlegungen.
5.3 Bedeutung der gegraphischen Längen von Hamburg und Wien ↑ Anfang
Gleichung (2) enthält die geographische Länge λ nicht, gilt also an jedem Ort gleichen Breitengrades φ.
Die geographischen Längen von Hamburg und Wien wurden in obigen Rechnungen lediglich als Längengrad-Differenz
λHamburg - λWien = 6,3° ausgewertet. Diese Rechenergebnisse gelten somit nicht prinzipell für den Moment des Sonnenaufgangs in Hamburg und in Wien, sondern prinzipiell nur für zwei Orte mit λ1 und λ2, die zwar auf den Breitengraden von Hamburg bzw. Wien liegen, sonst aber lediglich die gleiche Längengrad-Differenz (λ1 - λ2 = 6,3°
= ΔΤ-Bedingung) wie diese beiden Städte haben. An diesen zwei noch nicht bekannten Orten findet der scheinbare Sonnenaufgang genau zur gleichen Uhrzeit statt. Dabei hat die Sonnendeklination den mit der ΔΤ-Bedingung der Augabenstellung indirekt vorgegebenen Wert δgenau.
Umgekehrt gesagt: Mit der ΔΤ-Bedingung ist der Wert von δgenau indirekt vorgegeben und kann berechnet werden. Damit ist aber lediglich eine allgemeine Aussage gemacht: Wenn die Sonnendeklination den Wert δgenau hat, verläuft der Terminator (h= - 0,833°) durch zwei Orte auf den Breitengraden von Hamburg und Wien und mit gleicher Längengraddifferenz wie diese. In welcher Lage sich die Erde bei ihrer Drehung um die eigene Achse im Moment δgenau befindet, bedarf weiterer Klärungen.
Insgesamt handelt es sich um vier noch unbekante Orte: ein Paar für den 26. Mai und ein Paar für den 17. Juli. Denn, dass an einem Ortepaar nicht prinzipiell an beiden Kalendertagen genau gleicher Sonnenaufgang sein kann, wurde oben (Abschnitt 5.2) besprochen. Das Städtepaar Hamburg und Wien hat nur zufällig und in jährlich verschieden großer Näherung gleichzeitigen Sonnenaufgang. Weil sich die Sonnendeklination sehr langsam über den Tag ändert, ist der Zeitunterschied aber immer viel kleiner als eine Minute. Die Welt-Städte Hamburg und Wien wurden vermutlich anstatt anonymer Orte 1 und 2 gewählt, um etwas Anschaulichkeit in die Problematik zu bringen (Übrigens: In der Nähe von Hamburg bzw. Wien lebt je einer der beiden Aufgabensteller. [1]).
5.4 Berechnung von δgenau ↑ Anfang
Der Index ..genau ist für das folgende Ergebnis nicht ganz korrekt, da die Rechnung numerisch-iterativ erfolgen und willkürlich bei genügend erscheinender Näherung an den genauen Wert abgebrochen wird.
Der Wert von δgenau wird sich zwischen 21,14° und 21,17° (siehe oben in Abschnitt 5.2) befinden.
Ich beginne die Iteration mit δ = 21,14° und führe sie in Schritten Δδ = +0,01° durch.
Mit Gleichung (2) werden mit den geographischen Breiten von Hamburg bzw. Wien zwei Stundenwinkel berechnet und ihre Differenz ΔΤ = Τ1 - Τ2 schrittweise an ΔΤHW = - 6,3° genähert.
δ = 21,14°: ΔΤ = - 6,29754° ,
δ = 21,15°: ΔΤ = - 6,30179° .
Bis auf 2 Nachkommastellen ist bereits δ = 21,15° der gesuchte Wert für δgenau .
Für die Angabe mit 3 Nachkommastellen wäre mit δ-Vorgabewerten zwischen 21,14 und 21,15 weiter zu iterieren. Ich erspare mir den Aufwand und begnüge mich mit einer linearen Interpolation zwischen diesen Werten. >>>>
δgenau = 21,146° .
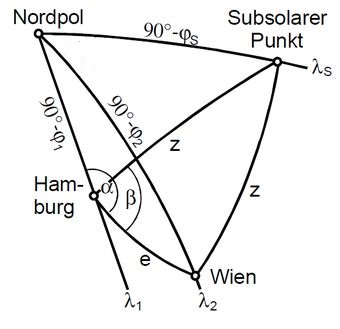
Rolf Wieland gibt in seiner Lösung (in [1, Juni 2018] leider nicht berücksichtigt) eine geschlossen und anschaulich durchführbare Berechnung von δgenau mittels sphärischer Trigonomie an (der Index ..genau ist nun korekt).
Er nutzt die Tatsache, dass die geographische Breite des Subsolaren Punktes [5] auf der Erdoberfläche im Moment des scheinbaren Sonnenaufganges gleich ist der Zenitdistanz der Sonne an den Orten 1 und 2: z = 90°- h. Die geographische Breite φs dieses Punktes ist zudem gleich dem Deklinationswinkel δgenau der Sonne bzw. deren "Breite" an der Himmelskugel.
Ich habe nachträglich auch auf diese Weise gerechnet und δgenau = 21,1455° ermittelt (mein vierstelliger obiger Wert vor dem Runden: 21,1456°).
Die links gezeigte Abbildung Wieland's (Großkreise auf Erdoberfläche) macht die obige Aussage, dass nicht die absoluten Längengradwerte von Hamburg und Wien eine Rolle spielen, sondern nur ihre Differenz (und die absoluten Breitengrad-Werte der beiden Städte), anschaulich. Ins Endergebnis geht nur die Größe e ein, die lediglich eine Funktion von (λ1 - λ2) ist.
Rolf Wieland hat nachträglich auch meine Rechnung geschlossen (anstatt numerisch/iterativ) durchgeführt und
δgenau = 21,1458° erhalten.
5.5 An welchen Orten ist der Sonnenaufgang genau gleichzeitig? ↑ Anfang
Diese Frage ist vergleichbar mit der nach dem Längengrad (das Längenproblem, [6]), die sich insbesonders für die Navigation von Schiffen auf den Ozeanen stellt. Das Problem konnte erst vor etwa 150 Jahren gelöst werden, als eine an Bord genau genug gehende Uhr konstruiert worden war, die die auf einem Bezugslängengrad eingestellte Zeit (die dortige Ortszeit bzw. die Sonnenzeit dieses Ortes) während einer längeren Reise einhalten konnte. Die Differenz mit der Sonnenzeit am momentanen Ort des Schiffes (z.B. 12 h Mittag bei Sonne im Zenit) ergibt den Längengrad diese Ortes (eine Stunde Zeitdifferenz entspricht 15° Längengraddifferenz; westlicher, wenn die Uhr später als 12 h zeigt und umgekehrt).
Die vorliegende Frage bezieht sich auch auf den jeweiligen Längengrad unbekannter Orte. Und diese kann ebenso mit Hilfe einer genau bekannten Uhrzeit ermittelt werden, nämlich mit der Wahren Sonnenzeit auf einem Bezugslängengrad im Moment der Sonnendeklination mit dem Wert δgenau .
Die relativ genaue Uhrzeit für δgenau = 21,146° wird für den 26. Mai aus der Tabelle [4] zu 04,376h MEZ interpoliert. Nach erfolgter Zeitgleichungs-Korrektur (+0,05h nach Tabelle [4]) ist für den Bezugslängengrad λ = -15° (Görlitz) die Wahre Sonnenzeit 04,426h .
Am unbekannten Ort auf Hamburger Breitengrad (φ = 53,6°) ist mit δgenau nach Gleichung (2)
Τ53,6 = - 123,4293° bzw. Wahre Sonnenzeit = 03,7714h .
Die Zeitdifferenz von 0,6546h (04,426h - 03,7714h) bedeutet, dass der unbekannte Ort auf dem Hamburger Breitengrad 9,8193° (0,6546h · 15°/h) westlicher als der Bezugslängengrad liegt. Relativ zu Hamburg liegt er 4,82° westlicher (9,8193° + 10° - 15°).
Der bisher unbekannte Ort auf dem Wiener Breitengrad liegt selbstverständlich ebenfalls 4,82° westlicher als Wien, denn δgenau = 21,146° gilt ja dafür, dass an Orten mit Δλ = 6,3° (wie zwischen Hamburg und Wien) und mit den beiden Breitengraden von Hamburg und Wien der Sonnenaufgang genau gleichzeitig ist.
Am 17. Juli liegen die beiden gesuchten Orte wesentlich westlicher als Hamburg bzw. Wien, nämlich 40,66°.
Einzige Änderung in der Rechnung ist der an diesem Kalendertag andere für δgenau = 21,146° interpolierte Wert für die
Wahre Sonnenzeit am Bezugsmeridian λ = -15°. Der Wert ist 06,815h (Anteil der Zeitgl.-Korrektur: -0,103h).
5.6 Wie groß ist der kleine Unterschied zwischen den Sonnenaufgangszeiten
in Hamburg und Wien?
↑ Anfang
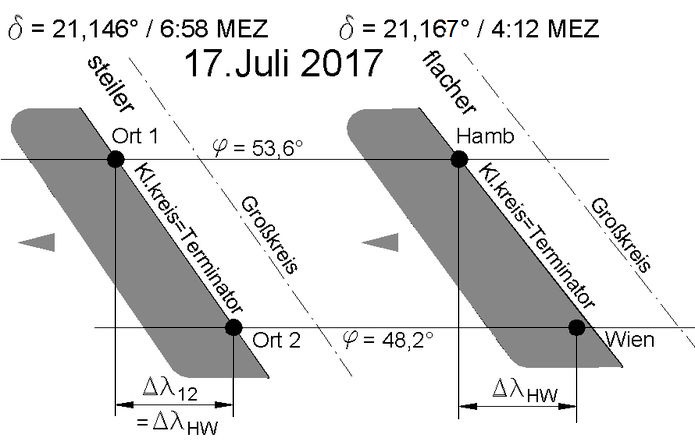
Am 17. Juli 2017 geht die Sonne in Wien etwa zwei Sekunden später auf als in Hamburg
(δ = 21,167°,
ΔΤHW = - 6,3088° (anstatt - 6,30°),
-0,0088° · 4min/° = -0,0352min ≈ -2,1sec;
oben unter 4. Lösung ein größerer Wert mit umgekehrten Vorzeichen, weil Näherung mit δ = 21,11° anstatt 21,167°).
Die Situation ist im nebenstehenden Bild schematisch dargestellt. Wien ist zur Zeit des scheinbaren Sonnenaufgangs ín Hamburg noch kurzzeitig im Schatten. Erst fast drei Stunden später hat sich der Terminator so weit "aufgerichtet", dass die beiden gleich weit wie Hamburg und Wien voneinander entfernten etwa 41° westlicheren Orte 1 und 2 genau gleichzeitigen Sonnenaufgang haben.
Der am 26. Mai errechenbare Unterschied ist kleiner als eine Sekunde und somit praktisch bedeutungslos.
5.7 Welche wären die genauen Sonnenaufgangszeiten in Hamburg bzw. in Wien? ↑ Anfang
Die Sonnenaufgangszeiten in Hamburg und in Wien sind bisher noch nicht genau bekannt. Sie unterscheiden sich um wenige Sekunden, wie die Näherungsrechnungen im Abschnitt 5.6 Wie groß ist der kleine Unterschied zwischen den Sonnenaufgangszeiten in Hamburg und Wien am 17. Juli 2017? zeigen. Um u.a. diesen kleinen Unterschied genau zu erhalten, müssten sie auf Bruchteile von Sekunden bestimmt werden. Ich gebe im Folgenden eine Vorgehensweise an, verzichte aber darauf, Rechnungen vorzunehmen.
Die beiden Zeitpunkte sind bisher noch nicht bekannt, weil sie nicht mit Hilfe der genauen zugehörenden Deklinationswerte der Sonne berechnet wurden. Man muss iterativ vorgehen, d.h. mit einem Deklinationswert beginnen, dessen Zeitpunkt dem vermuteten des Sonnenaufgangs nahe ist (z.B. mit δ04h wie im Abschnitt 5.6). Die nächste Rechnung (mit Gleichung (2) usf.) wird mit dem δ-Wert vorgenommen, der dem errechneten Zeitpunkt entspricht (Iteration in Tabelle [4]). Dieser Schritt erfolgt sooft bis die Änderung der errechneten Sonnenaufgangszeit als genügend klein erachtet wird.
Eine solche Rechenreihe ist sowohl für Hamburg als auch für Wien vorzunehmen, da ihre Sonnenaufgangszeiten nicht genau gleich sind.
6. Erkenntnis ↑ Anfang
Meine weiteren Überlegungen waren wohl qualitativ erhellend, aber quantitativ nur viel Lärm um fast Nichts.
Die Erkenntnis ist, dass sehr kleine Änderungen (der Sonnen-Deklination) über die Zeit und Zufälle
(die Sonnendeklination hat im Moment des Sonnenaufgangs an zwei Orten (Hamburg und Wien) und an einem bestimmten Kalendertag (26. Mai) den fast genau passenden Wert (21,143°))
das Verständnis eines Zusammenhangs sehr erschweren können.
7. Verweise ↑ Anfang
[1]: Gerold Porsche und Kurt Descovich: "Zum Nachdenken", sonne+zeit (Rundschreiben der Arbeitsgruppe
Sonnenuhren im österreichischen Astronomischen Verein), Nr. 54, Dezember 2017,
eine der eingesendeten Lösungen in Nr. 55, Juni 2018
[2]: Wikipedia: "Terrestrische Refraktion"
[3]: Wikipedia: "Astronomische Koordinatensysteme, 4.3 Umrechnungen: Ruhende äquatoriale (Τ, δ) → ...
→ horizontale Koordinaten (a, h)"
[4]: Helmut Sonderegger: "Tabelle der Sonnendeklination für das Jahr 2017" und "Zeitgleichung … für das Jahr 2017",
Beilage in sonne+zeit (Rundschreiben der Arbeitsgruppe Sonnenuhren im österreichischen Astronomischen Verein),
Nr. 52, Dezember 2016
[5]: Wikipedia: "Subsolarer Punkt"
[6]: Wikipedia: "Längenproblem"

8. Zusatzaufgabe ↑ Anfang
Bei der Zusatzaufgabe
Darstellung der Nacht-Tag-Grenze in einem
λ/φ -Diagramm
dachte ich an deren anschauliche Darstelung in "Geochron", einem sogenannten "Global Time Indicator" (Bilder links).
Anstatt auch diese Aufgabe zu lösen, verweise ich darauf.
Auf der Erdkugel ist die idealisierte Grenze (h=0) ein Großkreis (bei h < 0 ein ihm naher Parallelkreis), dessen Aussehen in einer Kartenprojektion von der Projektionsmethode abhängt (Geochron: Mercator-P., h=0). Im Laufe eines Jahres ändern sich in erster Linie die Winkelabweichung von der Nord-Süd-Linie (Hin-und Herkippen um einen Äquatorpunkt mit Rektaszension der Sonne +90° bzw. -90°, siehe Anmerkung).
In der Mercator-Projektion wechselt die Nacht-Tag-Grenze zwischen S- und ?-Form (s. Bilder links).
Dass es sich um einen solchen Punkt handelt, ergibt sich aus folgenden Überlegungen:
* Am Äquator ist der Tag das ganze Jahr über idealisiert gleich, nämlich 12 Stunden lang. Die Nacht-Tag- und die Tag-Nacht- Grenze teilen den Äquator in zwei gleich Teilstücke (zwei 180° Bögen, in der Mitte eines dieser Bögen befindet sich der Meridian mit der Sonne).
* Alle (sich mit der Deklination ändernden) Grenzlinien passieren diese beiden Teilpunkte (das ist leicht erkennbar, weil der subsolare Punkt im Meridian bleibt). Im Einzelnen pendeln sie jeweils in einem dieser Punkte hin und her.
![]() Siegfried Wetzel, CH 3400 Burgdorf, August 2018 (Okt.18, Apr.22)
Siegfried Wetzel, CH 3400 Burgdorf, August 2018 (Okt.18, Apr.22)
↑↑ Anfang
<< Home
<< andere Sonnenuhren-Beiträge