<< Home
<< andere Ostern-Beiträge

 ↓↓ Ende

Oster-Datum: Sonnen- und Mondgleichung

Veranlassung

Mehr Mühe hatte ich mit der Beschreibung der mit Hilfe dieser beiden Gleichungen verfolgten sachlichen Absicht. Insbesondere überlegte ich seit langem, wie die Rolle der Sonnengleichung bei der Findung des Frühlingsvollmond-Datums darzustellen ist, ohne Irritation zu erzeugen, beziehungsweise um bereits vorhandene Irritation zu beseitigen. Die folgenden Zeilen sind ein Versuch, die Zusammenhänge treffender als in der Literatur üblich darzustellen.

Darstellung

Der Julianische Kalender mit 6.939,75 Tagen für 19 Kalenderjahre (365,25 Tage für ein Kalenderjahr) und für 235 Mond-Monate (29,53085 Tage für einen Kalender-Monat) wird in seiner Version als Gregorianischer Kalender immer wenigstens 100 Jahre angewendet, bevor eine Korrektur erfolgt. Die Menge der zugrunde liegenden Tage ist sowohl für das im Kalender möglichst genau zu verwirklichende tatsächliche Sonnenjahr als auch für den tatsächlichen Mond-Monat (Lunation) geringfügig zu groß, was die seltenen Korrekturen mit Hilfe der Sonnen- und der Mondgleichung erfordert.Die Korrekturen führen zu den Durchschnittswerten 365,2425 Tagen für das Kalenderjahr (astronomisch: 365,24219 Tage) und 29,530587 Tagen für den Mondmonat im Kalender (astronomisch: 29,530589 Tage).

Der Julianisch/Gregorianische Kalender (unser Kalender) ist primär, das heißt für seinen bürgerlichen Gebrauch, ein Sonnenkalender. Er hat mit den vom Jahreslauf der Sonne vorgegebenen Jahreszeiten konform zu gehen. Im Detail heisst das, dass sein Kalenderjahr die Länge des tatsächlichen Sonnenjahres gut nachbildet und dass sich ein tatsächlicher (astronomischer) Referenzpunkt im Kalender auch langfristig nicht verschiebt. Zum Beispiel soll sich der astronomische Frühlingsanfang (die Sonne im Widderpunkt) immer mit dem 21.März decken. Auf den Mond wird in einem Sonnenkalender keinerlei Bezug genommen. In einem reinen Mondkalender (z.B. im Islamischen Kalender) ist ausschließlich der tatsächliche Mond (einer seiner Phasenzeitpunkte) im Kalender richtig anzugeben. In einem gebundenen Mondkalender wird auch primär auf den Mond Bezug genommen, die Bindung an die Sonne ist aber die sekundäre Aufgabe. Im Jüdischen Kalender wird das deutlich, in dem der Frühlingsvollmond den 14.Nisan als fixes Kalenderdatum hat (der Frühlingsanfang hat immer ein variables Datum).

In unserem Kalender werden alle Daten auf den Sonnenlauf bezogen angegeben. Das ist der entscheidende Punkt. Wird eine Korrektur bezüglich der Sonne vorgenommen, so müssen die Daten für den Mond "gerettet" werden. Die Anwendung der Sonnengleichung ist für den Mond mit umgekehrten Vorzeichen vorzunehmen. Anders ausgedrückt: Es ist dafür zu sorgen, dass eine solche Kalenderkorrektur die astronomischen Zeitpunkte von Mondphasen nicht verfälscht. Die in einem längereren Zeitraum (länger als der für die erforderliche Anwendung der Sonnengleichung) beim Mond entstandene Verschiebung der zyklischen (in einem Kalender angegebenen) Folge gleicher Mondphasen gegenüber der astronomisch bestehenden Folge wird ausschliesslich mit der Mondgleichung erfasst und korrigiert. Es besteht keinerlei Zusammenhang zur Sonnengleichung. Andererseits hat die Anwendung der Mondgleichung auch keinerlei Einfluss auf den Sonnenkalender.

Zusammenfassung in Bezug auf die Gregorianische Osterrechnung

Acht mal in 2.500 Jahren wird die Mondgleichung angewendet. Die Zeitpunkte für die Mondphasen (z.B. der Zeitpunkt des Frühlingsvollmondes) bekommen je einen früheren Tag im Kalender (Schema unten: x. März/April →
(x-1). März/April, z.B. 24.3 → 23.3. im Jahr +312).
In manchen Säkularjahren sind sowohl die Sonnen- als auch die Mondgleichung anzuwenden. Beide heben sich gegenseitig auf. Es erfolgt keine Änderung der im Kalender angegebenen Zeitpunkte für die Mondphasen. Mondalter und Epakte ändern sich in solchen Jahren nicht.

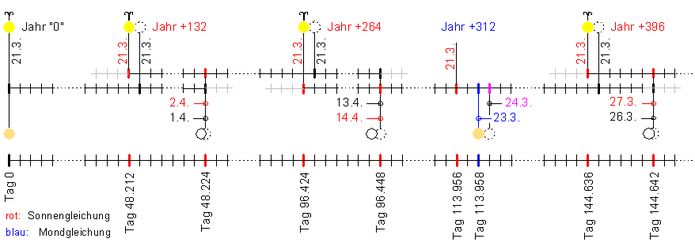
Im abgebildeten Schema habe ich die Anwendung der Sonnengleichung nach jeweils 132 Jahren und der Mondgleichung nach 312 Jahren dargestellt. Das sind annähernd die angewendeten Durchschnittswerte, und es erlaubt, das prinzipielle Vorgehen deutlicher darzustellen, als bei Befolgung der amtlichen Säkularjahrpraxis. 132 ist nahe bei 133 1/3, dem Mittelwert der amtlichen Praxis. Es ist ein Jahr, in dem der sonst fällige Schalttag ausfallen kann. Zudem bestehen 132 Jahre (Sonnengleichung) und 312 Jahre (Mondgleichung) und ihre ganzzahligen Viellfachen aus einer ganzen Zahl von Kalendertagen. Auf der mitlaufenden Zeitskala, die in Tagen unterteilt ist, lassen sich die Ereignisse ganzzahlig benennen.

Die Anwendung der Sonnengleichung heisst wie bei der Sekularjahrregelung auch, im entsprechenden Jahr den sonst fälligen Schalttag wegfallen zu lassen. In der Kalender-Skala wird bei jeder Anwendung ein Tag ausgeschnitten, denn der Frühlingsanfang (Widderpunkt) findet nicht z.B. am Tag 48.213, sondern einen Tag früher statt. Die nicht betroffenen Vollmondtage müssen aber auf der zurück geschobenen neuen Skala um einen Tag in die Zukunft verschonen werden
(x → (x+1)).

Nach 312 Jahren (dass es sich um ein Schaltjahr handelt, ist ohne Belang) scheinen die tatsächlichen Vollmonde inzwischen einen Tag früher als auf der Kalender-Skala vorausgesagt. Ihr Eintrag erfolgt auf diesen einen Tag früher
(x → (x-1)).

Anhang zum Schema

<<< Home
<< andere Ostern-Beiträge