<< Home
<< andere Getriebetechnik-Beiträge

 ↓↓ Ende

Kardangelenk und Sonnenuhr

Einleitungung

Die Gleichung für die Stundenlinien einer horizontalen Sonnenuhr mit Polstab und die Gleichung für den Drehwinkel einer über ein Kardangelenk angetriebenen Welle sind prinzipiell identisch.

Die Bewegungsgleichung des Kardangelenks ist auch in der Gleichung wiederzufinden, die bei der Behandlung der Zeitgleichung zum Übertragen der in der Ekliptik stattfindenden scheinbaren Bewegung der Sonne auf die Bewegung einer Ersatzsonne auf dem Himmelsäquator benutzt wird. Ist es auf Grund dieser Übereinstimmungen möglich, in einem einfacheren Modell als in einem Tellurium die Bewegung der Erde mit Hilfe eines Kardangelenks zu erzeugen, so dass auf deren Oberfläche die Jahresspur des Subsolaren Punktes als Analemma-Figur (Anmerkung 1) sichtbar wird?

Inhalt

1. Ein Äquationsuhren-Entwurf  ↑ Anfang

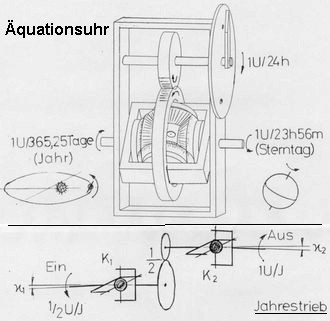
<< Abb.1 Entwurf einer Äquationsuhr

In einer früheren Arbeit ([1] (Abb.1)) zeigte ich den Entwurf einer mechanischen Uhr, die dem Lauf der wahren Sonne am Himmel folgt. Es handelte sich um eine sogenannte Äquationsuhr, die um die Differenz der wahren Sonne gegen den gleichmäßigen Lauf der Zeit beziehungsweise der sogenannten mittleren Sonne "ungenau gehend" gemacht wurde. Die Zeitgleichung ist in ihr in umgekehrter Weise wie in einer korrigierten Sonnenuhr berücksichtigt. Im Nachhinein erwies sich, dass die damals gemäß einer anderen Arbeit ([2]) angestrebte Näherung mit zwei sinusförmigen Funktionen der Zeit mit Hilfe von zwei Kardangelenken übertroffen wurde. Die Übertragungs-funktion eines Kardangelenks ist nämlich nicht sinusförmig, sondern exakt für die Simulation der Wirkung der zweiten Zeitgleichungs-Ursache (Bewegung der Sonne auf der Ekliptik, nicht auf dem Himmelsäquator) geeignet.

Ich war überrascht, als ich in der von mir damals ([1], Erstversion Dez.07) hergeleiteten Gleichung
(7)   α(t) = arctan ( tan Λ(t) · cos ε )
die für das Kardangelenk bekannte Wellenwinkelgleichung
(7a)  φ₂ = arctan ( tan φ₁ · cos κ )
erkannte ([1], Version Okt.13: Anhang 4).

2. Hilfsgerät zum Zeichnen von Sonnenuhren-Zifferblättern   ↑ Anfang

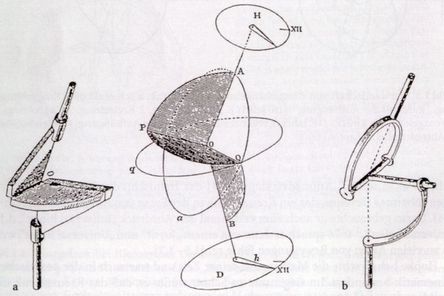
Abb.2 Hilfsgerät zum Zeichnen von Sonnenuhren-Zifferblättern;
          links: [3 (Seite 4)]
          rechts: [4 (18. Das Hookesche Instrument)]

Nachdem ich mich genauer mit der zum Himmelsgeschehen passenden Kinematik des Kardangelenkes befasst hatte, erinnerte ich mich auch wieder daran, dass Robert Hooke (englischer Universalgelehrter des 17. Jahrhunderts, bekannt durch das Elastizitätsgesetz: Linearität zwischen Materialdehnung und Spannung im Material) ein Hilfsgerät mit Kardangelenk zum Zeichnen der Stundenlinien auf dem Zifferblatt einer horizontalen Sonnenuhr mit Polstab hergestellt und verwendet hatte.

Abb.2 bezieht sich im linken Bild auf das Hookeschen Gerät: links ein aus Scharnieren bestehendes, rechts ein fast vollständig ausgebildetes Kardangelenk üblicher Konstruktion (vollständige Gabel anstatt Halbgabel unten, vollständiges Kreuz anstatt T-Stück in der Mitte). In Bildmitte ist die Funktion des Zeichengerätes schematisch dargestellt: Der obere Kreis ist äquatorparallel. Sein Zeiger ist gegen die Sonnne gerichtet. Gegen die Mittagsrichtung XII der Sonne bildet er den Stundenwinkel τ. Der untere Kreis liegt in horizontaler Ebene. Sein Zeiger deckt sich mit der zu τ gehörenden Stundenlinie. Mit der Stundenlinie XII bildet er den Winkel α. Der Winkel zwischen den beiden Wellen ist der Beugewinkel κ bzw. der zu 90° komplementäre Winkel der geographischen Breite φ. Im rechten Bild von Abb.2 ist ein moderner Nachbau dieses Gerätes gezeigt: Vorne befindet sich die äquatorparallel zu haltende und auf die Sonne zu drehende Scheibe, mit der über das Kardangelenk ein Zeiger auf dem Sonnenuhrenzifferblatt eingestellt wird. Entlang des Zeigers wird die Stundenlinie gezeichnet.

Die Funktion diese Gerätes ist zwingend, denn die geläufige Zifferblattgleichung (horizontales Zifferblatt)
α = arctan ( tan τ · cos (90°-φ) )    [5]
unterscheidet sich tatsächlich nicht von der Wellenwinkelgleichung des Kardangelenks (7a).

3. Subsolararer Punkt als Analemma in zwei Modellen   ↑ Anfang

Die Anregung für meine intensivere Beschäftigung mit dem Kardangelenk gab ein Modell, in dem die Wirkung der ekliptikalen Ursache (eine von zwei Ursachen) der Zeitgleichung als Analemma-Figur unter Verwendung eines Kardangelenkes auf einen Erdglobus gezeigt wurde [7]. Im genannten Modell wird das Analemma als Jahresspur des Subsolaren Punktes auf der Erdoberfläche, die gleich aussieht wie die Jahresspur des täglich zum gleichen Zeitpunkt beobachteten Sonnenstands an Himmel, dargestellt.

Das Modell mit Kardangelenk war als Ersatz für ein größeres und weniger leicht zu transportierendes Tellurium, mit dem einige Zeit vorher das gleiche Experiment vorgenommen worden war [6], gedacht. Das ältere Experiment wird im Folgenden zuerst besprochen.

4. Tellurium und Analemma    ↑ Anfang

Abb.3 Tellurium mit Sonne und Erde

<< Abb.4 Tellurium mit Sonne und Erde
               Analemma-Figur (Subsolarer Punkt) auf dem                    Erdglobus

Ein am Ort der Sonnenkugel montierter, gegen den Globus gerichteter Laserpointer, zeichnete die Analemma-Figur auf dem Globus des Telluriums nach. Die Tagesdrehung der Erde war "angehalten" worden. Genauer: Der Globus drehte sich nicht ca. 365 mal während er ein mal um die zentrale Sonnenkugel geführt wurde, sondern drehte sich dabei nur ein mal, so dass er sich von der Sonnenkugel aus gesehen nicht um die eigene Achse drehte. Es war nicht nötig, jeden Tag einen bestimmten Zeitpunkt zum Zeichnen des Subsolaren Punktes abzupassen. Das Zeichnen der analemmaförmigen Spur des Subsolaren Punktes auf dem Globus wurde zu einem stetigen Vorgang.

Abb.3 zeigt die Wiederholung des Versuchs [7] mit einem eigenen Minimal-Tellurium. Den Subsolaren Punkt zeichnete ich auf dem Globus mit Hilfe eines auf dem Telluriumarm montierten Zeigers mit Loch für eine Schreiberspitze nach: Abb.4, Getriebeaufbau in Anmerkung 2.

5. Kardangelenk und Analemma   ↑ Anfang

Das lediglich aus einem auf einem Kardangelenk gestützten Globus bestehende Modell [7] wurde auf der letzten Jahrestagung der Arbeitsgruppe Sonnenuhren im Österreichischen Astronomischen Verein vorgestellt und damit ein dem Subsolaren Punkt folgendes Analemma auf dem Globus gezeichnet. Ich hielt den Einsatz eines Kardangelenkes für diesen Zweck als eine logische Folge der von mir erst kürzlich erkannten formalen Verwandtschaft zwischen ihm und der Behandlung der zweiten Zeitgleichungsursache ([1], Anmerkung 4).

5.1 Versuchs-Wiederholung   ↑ Anfang

Abb.6 zeigt einen Nachbau dieses Modells. Der Arm des Telluriums (Abb.3) und die Antriebe von ihm aus sind weggefallen. Festes Element und Teil des Referenzsystems ist die Welle 1 unter dem Kardangelenk. Ursprung des Referenz-x-y-z-Koordinatensystems ist der Mittelpunkt der Sonne, die Ekliptik (in der sich auch der Erde/Globus umgebende blaue Ring befindet) ist die x-y-Ebene, die x-Achse führt durch den Erd-/Globusmittelpunkt.

Der Globus ist im Nachbau auf einem durch seine Drehachse gehenden Großkreis genutet. In die Nut greifen zwei einander gegenüber liegende Stifte, die darin gleiten, aber sich auch um ihre gemeinsame Mittellinie drehen können. Die Stifte sind an den Enden eines die Kugel tragenden, zur Welle 1 gehörenden Bügels befestigt. Sie bilden gemeinsam ein Drehgelenk. Ein übliches Kardangelenk hat zwei weitere Stifte, die ein zweites Drehgelenk bilden. Die vier Stifte sind in einem kreuzförmigen Zwischenteil im Kardangelenk vereinigt, das deswegen auch Keuzgelenk heißt. Das zweite Drehgelenk entsteht durch das Gleiten der beiden Stifte in der Nut. In beweglichen Bauteilketten (Getrieben) entfällt grundsätzlich immer ein Bauteil dann, wenn eins der Gelenke zwei Beweglichkeiten (im vorliegenden Fall zusätzliches Gleiten zum Drehen) bekommt. Das hier verwendete Kardangelenk hat deshalb kein zwischengesetztes Drehgelenk-Kreuz.

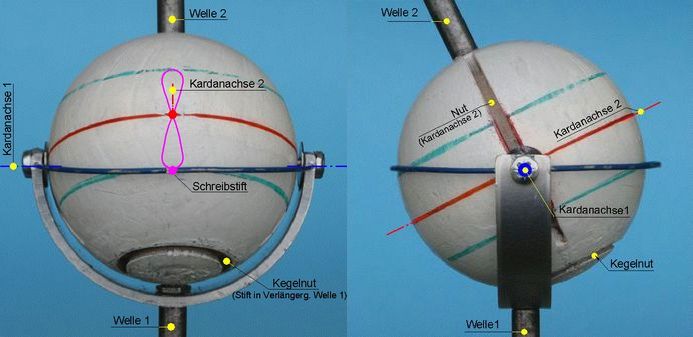Abb.6 Bewegungs-Modell der Erde mit Kardangelenk

Das Modell wird so aufgestellt, dass die x-Achse senkrecht auf die untere Kardankreuz-Achse trifft. Der Globus (Erde) wird periodisch bewegt, indem sein Stiel (Welle 2 über dem Kardangelenk) von Hand auf einem Kegelmantel (Spitze in der Kugelmitte, halber Kegelwinkel ε = 23,5°) herum geführt wird. Die Führung wird durch einen Stift-Fortsatz an der Welle 1 gewährleistet, der in eine Nut ("Kegelnut" auf dem südlichen Polarkreis des Globus) eingreift. Ein in x-Richtung blickender Beobachter erkennt, dass sich ein auf einer blauen Ringhälfte mittig liegender Punkt auf einer symmetrisch über dem roten Kreis (Äquator der Erde) liegenden Analemma-Figur bewegt, die als Spur des Subsolaren Punktes gedeutet wurde.

5.2 Kritik zur Deutung der beobachteten Analemma-Figur   ↑ Anfang

Die mit dem Modell [7] und mit seinem Nachbau (Abb.6) bei bestimmter Orientierung des Kardangelenkes erzeugte Spur hat prinzipiell die Form eines symmetrischen Annalemmas. Dass sie nicht die zu erwartende, sondern etwa die doppelte Breite hat, wurde sowohl vom Autor zu [7] als auch von mir vorerst übersehen, und der Frage, warum Form und Größe des Analemmas nicht an allen Stellen des Äquators gleich sind, wurde nicht nachgegangen. Beide Phänomene wurde erst untersucht, als der Autor zu [4] auf die doppelte Breite hingewiesen hatte.

Erste Bestätigung des Modell-Fehlers liefert eine Rechnung:
Unter Verwendung von Gleichung (7) wird mit Λ = ±45° (etwa zwei von 4 Maximum-Stellen im Jahr, Anmerkung 3) und ε = 23,5° für die Differenz α - Λ = ∓ 2,48°   ermittelt.
Die beobachtete Figur hat etwa ± 5° Breite. Sie verkleinert sich von ± 5° an den Durchstoßpunkten der oberen Kardankreuz-Achse zu 0° - einem Strich - an den Durchstoßpunkten der unteren Kardankreuz-Achse.

5.3 Gleichlaufgelenk und Analemma   ↑ Anfang

Dass ein Kardangelenk anstatt eines Gleichlaufgelenks im Modell eingebaut war, wurde bald als Quelle des Misserfolges vermutet. Diese Vermutung wurde zuerst experimentell bestätigt, und die entsprechenden theoretischen Überlegungen wurden später angestellt.

Im Nachbau-Modell (Abb.7) wurde das Kardangelenk durch ein simples Gleichlaufgelenk aus einem Zahnrad und einem "Zahnkranz" aus Nägelköpfen ersetzt. Die damit erzeugte Analemma-Figur hat die richtige Breite, und sie ist an allen Stellen des Äquators gleich.

Abb.7 Bewegungs-Modell der Erde mit Gleichlaufgelenk (Winkel zw. Zahnrad und Nagelkopf-"Zahnkranz" = 23,5°),
          Vorrichtungen zum Bewegen des Globusstiels (Welle 2 des Gleichlaufgelenks) auf einem Kegelmantel und
                               zum Positionieren eines Schreibstiftes demontiert.

5.4 Erklärung der beobachteten Analemma-Figuren   ↑ Anfang

Mit dem reduzierten Modell [7] sollte der gleiche Versuch wie mit dem Tellurium vorgenommen werden. Es sollte damit wie mit Letzterem die analemmaförmige Spur des Subsolaren Punktes (ohne den durch die elliptische Erdbahn verursachten Anteil) gezeichnet werden. Der Umbau hatte die im Tellurium richtig simulierte Bewegung der Erde relativ zur Sonne zu übernehmen. Es handelt sich um zwei kombinierte Bewegungen:

1. Die auf der Ekliptikebene geneigt stehende Erdachse dreht sich gleichmäßig einmal pro Jahr um eine zur Ekliptikebene senkrecht stehende Achse. Erd- und Drehachse schneiden sich im Erdmittelpunkt. Die Erdachse dreht sich, und sie taumelt. Im Tellurium dreht sie sich mit ihrem gleichmäßig drehenden geknickten Halter. Auf diesem ist sie schräg montiert, was das Taumeln bewirkt.
   Bei Berücksichtigung der elliptischen Erdbahn wäre die Drehung nicht gleichmäßig.


2. Die Erde dreht sich einmal pro Jahr um ihre eigene Achse mit gegenüber ihrer Achsdrehung (s. 1.) umgekehrten Richtung. Im Tellurium wird diese gleichmäßige Drehung vom drehenden Halter mittels drei gleich großer Zahräder erzeugt. Deren gleiche Größe bedeutet Übersetzung 1:1, das dritte (Zwischen-)Rad verursacht die Umkehr der Drehrichtung.
   Das gleichmäßige Drehen der Erde um ihre eigene Achse ist keine vereinfachende Annahme sondern entspricht der Wirklichkeit. Vereinfachende, weil für den Versuch praktische Annahme ist nur die Reduktion der Zahl der Tage im Jahr auf 1 Tag, die "angehaltene" Erde.

Die Kombination der beiden Bewegungen führt dazu, dass die Erde der Sonne das immer gleiche Gesicht zeigt. Sie scheint nur zu taumeln, sich aber nicht um sich selbst zu drehen. Das Taumeln bewirkt die analemmaförmige Spur des Subsolaren Punktes auf der Erdoberfläche.

<< Abb.8 Bewegungs-Modell der Erde mit Kardangelenk
               und Globusachse
               (vgl. Abb.6: bisherige Ausführung)

     links:
     halbe (oberer Teil) Globusachse ,
     drehbar in Welle 1 gelagert (dadurch Führung mit
     "Kegelnut" nicht mehr erforderlich)

     rechts:
     zusammen gesteckt (kegliger Hohlraum im Globus als
     Freiraum für den Lagerstift an der Globusachse)

Die Erdachse war im Modell [7] und in meinen Nachbauten nicht vorhanden. Sie ist für die angestrebte Bewegung des Globus materiell nicht erforderlich, aber die unter 1. besprochene Bewegung bleibt unerkannt. In Abb.8 ist diese nachträglich ins Modell mit Kardangelenk eingebaute Globusachse zu sehen. Bei der Versuchsdurchführung wird jetzt die unter 2. genannte Drehung des Globus um seine eigene Achse sichtbar und auch spürbar, wenn man beim Bewegen des Modells sie und nicht den sie umschließenden Stiel des Globus anfasst. Und es wird jetzt auch einsichtig, dass das Festhalten des Globus mit einem Kardangelenk an der Welle 1 nicht bewirken kann, dass er sich gleichmässig um seine sich selbst drehende und taumelnde Achse dreht. Seinem Drehen ist der sogenannte Kardanfehler überlagert.

Wie im Tellurium (Abschnitt 4, Abb.3 und Anmerkung 2, Abb.5 (rechts)) wird in meinem verbesserten Modell (Abschnitt 5.3, Abb.7) auch mit Zahrädern gearbeitet. Zahnräder übertragen Drehungen gleichmäßig. Ein sogenanntes Gleichlaufgelenk ist ein kompaktes Bauelement zur gleichmäßigen Drehübertragung zwischen abgewinkelten Wellen. Es beruht in allen Bauformen mit nicht-elastischen Teilen prinzipiell auf einer Zahnradpaarung. Mein in meinem Modell ausreichend funktionierendes Gleichlaufgelenk (Anmerkung 4) ist deutlich als eine solche Paarung erkennbar.

5.5 Konstruktion von Analemma-Figuren mit überlagertem Kardanfehler   ↑ Anfang

Das als Spur des Subsolaren Punkts auf dem Globus erkennbare Analemma hat seinen Kreuzungspunkt in den Momenten der Tag/Nacht-Gleichen (Globusachse nach rechts oder links geneigt). In den Momenten der Sonnenwenden liegt der Subsolare Punkt im obersten bzw. untersten Punkt des Analemmas (Globusachse nach vorn bzw. nach hinten geneigt).

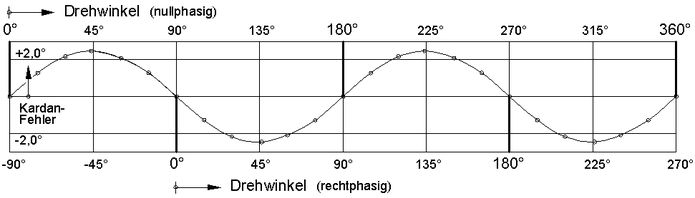Abb.9 Kardangelenk: Kardanfehler als Funktion des Drehwinkels (Knickwinkel = 23,5°)

Die Darstellung des Kardanfehlers (Vor- bzw. Nachlauf der getriebenen gegenüber der treibenden Welle, Welle 2 gegenüber Welle 1) als Funktion des Drehwinkels (Abb.9) ist abhängig davon, wie der Nullpunkt für die Angabe des Drehwinkels gewählt wird. Bezugsebene ist die Ebene, in der beide Wellen liegen. Bei der sogenannten nullphasigen Anfangslage ist der Drehwinkel 0°, wenn die Kardanachse 1 (s. Abb.6) in der Bezugsebene liegt. Bei der sogenannten rechtphasigen Anfangslage liegt sie senkrecht zu dieser Ebene, wenn der Drehwinkel 0° ist [3 (Seite 7)]. Ab 180° wiederholt sich die Abhängigkeit des Kardanfehlers vom Drehwinkel.

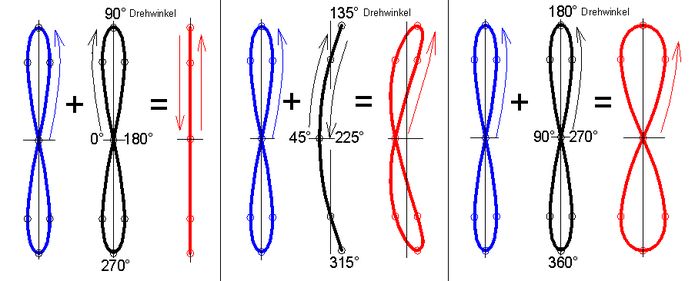Abb.10 Modell mit Kardangelenk: durch Überlagerung zweier Einzel-Figuren entstehende analemmaförmige Figuren

In Abb.10 ist in der Mitte jedes der 3 einzelnen Bilder der Kardanfehler als analemmaförmige Figur dargestellt: Kardanfehler auf der x-Achse (positiv nach rechts), Deklinationswinkel des Globus auf der y-Achse (positiv nach oben, Drehwinkel zusätzlich vermerkt). Diese Figur (schwarz) wird dem links stehenden Analemma (blau) des Subsolaren Punktes überlagert. Das Ergebnis ist jeweils genau diejenige Figur (rot), die beim Bewegen des Globus im Modell [7] und meinem Nachbau (Abb.6) sichtbar wird:

1. Rechtes Teilbild: Über einem Durchstoßpunkt der Kardanachse 2 auf dem Globus liegend (links in Abb.6 mit im Versuch ermittelter Figur). Drehwinkel rechtphasig gezählt.
2. Linkes Teilbild: Über einem Punkt auf dem Äquator des Globus liegend, der gegenüber oben (1.) genanntem Duchstoßpunkt der Kardanachse 2 um 90° verschoben ist. Drehwinkel nullphasig gezählt.
   Der resultierende gerade Strich liegt zwischen den Wendekreisen über der Nut im Globus.
3. Mittleres Teilbild: Über einem Punkt auf dem Äquator des Globus liegend, der gegenüber oben (1.) genanntem Duchstoßpunkt der Kardanachse 2 um 45° nach links° verschoben ist.
   Diese resultierende Figur hat die Breite der Spur des Subsolaren Punktes, ist aber in vertikaler Richtung gekrümmt. Die entsprechende Figur bei Verschiebung um 45° nach rechts ist umgekehrt gekrümmt.

6. Resumé   ↑ Anfang

Das geringfügig ungleichmäßig zwischen zwei nicht fluchtenden Wellen übertragende Kardangelenk ist geeignet, die wahre Sonnenzeit (ihre Abweichung von der gleichmäßigen Zeit wird mit Hilfe der Zeitgleichung beschrieben) in einer Äquationsuhr darzustellen.

Auf Grund dieser Anwendung anzunehmen, dass das Kardangelenk auch in einem Modell zur Darstellung der Spur des Subsolaren Punktes auf einem Globus geeignet sei, war ein Fehlschluss. Es ist dort unnötig, denn die Spur des Subsolaren Punktes ergibt sich daraus, dass sich der Globus gleichmäßig um seine sich drehende geneigte - eine taumelnde - Achse dreht. Das ungleichmäßig dreh-übertragende Kardangelenk ist lediglich als Erklärungshilfe für die scheinbare Ungleichmäßigkeit geeignet, die sich in der analemma-förmigen Spur des Subsolaren Punkts zeigt.

Die Eignung des Kardangelenkes zum Zeichnen der Stundenlinien auf dem Zifferblatt eine Postab-Sonnenuhr wurde bereits vor etwa 350 Jahren erkannt und in einer praktischen Vorrichtung benutzt.

7. Literatur   ↑ Anfang

[1] S.Wetzel: "Die Zeitgleichung für Nicht-Astronomen", DGC-Mitteilungen Nr.111, Herbst 2007
[2] S.Wetzel: "Eine elementare Behandlung der Zeitgleichung", DGC-Mitteilungen Nr.109, Frühjahr 2007;
     Chronométrophilia No 62, 2007
[3] Seherr-Thoss, Schmelz, Aucktor: "Gelenke und Gelenkwellen", Springer, 2002
[4] Rolf Wieland: "Selbst gebaute Sonnenuhren, Teil 3", Blog HELIOS-Sonnenuhren, Juni 2013
[5] S.Wetzel: "Sonnenuhr und Mathematik: 2. Die Polstab-Sonnenuhr und ihre Grundgleichung ",
     DGC-Jahresschrift 1999
[6] Harald Grenzhäuser: "Ein weiteres Modell zum Verständnis der Zeitgleichung",
     DGC-Mitteilungen Nr.135, Herbst 2013, S. 30 ("Aus dem Fachkreis Sonnenuhren. Tagung  9. - 11. Mai 2013")
[7] Harald Grenzhäuser: GSA-Rundschreiben Nr. 46, Dezember 2013 ("Tagung 20. - 21. September 2013")
[8] W. Reuthe: "Die Bewegungsverhältnisse bei Kreuzgelenkantrieben", Konstruktion, 2.(1950), Heft 10, S. 305

8. Anmerkungen   ↑ Anfang

Anmerkung 1:    ↑ zurück

Der Begriff Analemma wird in der vorliegenden Arbeit einschränkend gebraucht. Die allgemein bekannte Analemma-Figur (der über ein Jahr täglich zu einem gleichen Zeitpunkt aufgenommene Sonnenstand) berücksichtigt beide Ursachen dafür, dass die Sonne nach Ost bzw. West von einer mittleren Lage abweicht (Zeitgleichung). Hier bleibt aber der aus der elliptischen Erdbahn folgende Anteil für diese Ost/West-ausschläge unberücksichtigt. Das derart eingeschränkte Analemma ist eine sowohl in seiner Häöhe als auch in seiner Breite symmetrische Figur (auch eingeschränkt auf der Erdoberfläche, wo es den wechselnden Sonnenstand als wechselnden Subsolaren Punkt markiert).

Anmerkung 2:    ↑ zurück

Abb.5 Zahnradgetriebe des Telluriums
           links:  "vereinfachte Normalversion" mit 14 Tagen pro Jahr (2 Wochen anstatt 365¼ Tage pro Jahr)
           rechts: für in Abb.3 gezeigtem Versuch (1 Tag pro Jahr)

Links im Bild ist eine zweistufige Zahnradübersetzung ins Schnelle eingebaut. Sie beträgt 1:16, ausgehend vom unter dem Kettenrad liegenden und zusammen mit ihm drehenden Zahnrad (z=40). Durch die Hohlachse des Kettenrades hindurch wird die schnelle Drehung über das 1:1-Getriebe auf die Globuswelle übertragen. Der Globus dreht sich 14 mal, wenn sich der Telluriumarm einmal dreht. Von den 16 Drehungen der in der Hohlachse liegenden Welle gegenüber dem Fuß des Telluriums gehen zwei bei der Übertagung auf den Globus verloren: eine durch das Abwälzen des Zahnrades unter dem Globus auf seinem Gegenrad und eine, weil das Tagesdrehen des Globus (der Erde) relativ zum Arm (zur Sonne, nicht zum Halter des Globus bzw. nicht zu den Sternen) gezählt wird. In dieser "vereinfachten Normalversion" hat das Jahr 14 Tage.

Für 1 Tag pro Jahr habe ich anstatt die Übersetzung von 1:16 auf 1:2 wie in [6] zu ändern, das 1:1-Getriebe unter dem Globus mit einem Zwischenrad versehen (rechts im Bild). Das Übersetzungsgetriebe ins Schnelle ist unwirksam und größtenteils abmontiert. Die in der Hohlachse liegende Welle ist mit einer Blechzeiger am Telluriumarm gefesselt.

Anmerkung 3:     ↑ zurück

Die Stelle des Höchstwertes der Differenz liegt nicht genau bei Λ = ± 45°. Sie wird nach folgender Gleichung berechnet:
cot Λ = (cos ε)^½ [8].
Für  ε = 23,5°  ist  Λ = ± 46,2°.

Anmerkung 4:     ↑ zurück

Das von mir verwendete Gleichlaufgelenk ist eine Vereinfachung der im Maschinenbau oft benutzten Bogenzahnkupplung. In einer solchen Kupplung ist ein in einer innenverzahnten langen Hülse steckendes Zahnrad wegen des zu übertragenden relativ hohen Drehhmoments viel dicker als das von mir verwendete. Damit die relativ langen Zähne in einer Bogenzahnkupplung bei der Abwinklung zwischen Hülsen- undr Rad-Achse nicht klemmen, sind die Zähne des Rades in Achsrichtung nicht gerade, sondern bogenförmig gestaltet.

9. Nachtrag   ↑ Anfang

In Abb.11 ist ein Kardangelenk gezeigt, das einfacher konstruiert ist als das in den Abb.n 6 und 8 gezeigte. Es handelt sich um ein Kugelgelenk, dem eine seiner drei Dreh-Freiheiten genommen ist: Schlitz in der Kugelschale, in der ein in der Kugel befestigter Mitnehmerstift gleitet. Auf die Kugel (Globus) sind mit Filzschreiber die in Abb.10 rot dargestellten Figuren gezeichnet.

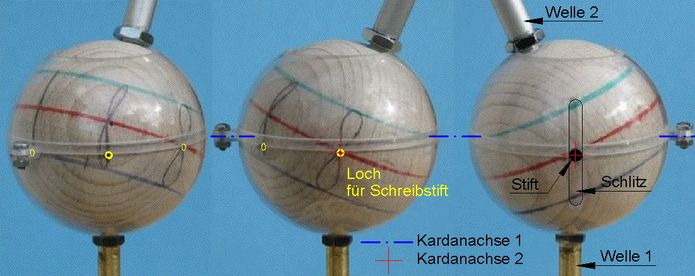Abb.11 Bewegungs-Modell der Erde mit vereinfachtem Kardangelenk

Siegfried Wetzel, CH 3400 Burgdorf, November 2013 (Dez.14, Jan.20)

 ↑↑ Anfang

<< andere Getriebetechnik-Beiträge
<< Home