<< Home
<< anderes Geometrisches
  ↓↓ Ende

Windräder

Zusammenfassung

Die Grundform ist der Würfel. Die Drehachse ist senkrecht wie beim bekannten mit Kugel-Halb-Schalen ausgerüsteten Messgerät für die Windgeschwindigkeit (Schalenkreuzanemometer). Solche Windräder müssen nicht wie die viel häufigeren Propeller-Windräder mit einer Wetterfahne in den Wind gestellt werden. Das zuerst gebaute Windrad ist ein einzelner auf der Spitze stehender Würfel. Später fügte ich drei Würfel zu einer Würfelecke zusammen. Bei den davon abgeleiteten Varianten habe ich Teile der Würfel entfernt. Zuletzt entstand eine Kombination aus vier Würfeln.

Inhalt

1. Ein-Würfel-Windrad   ↑ Anfang

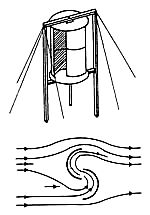
Die Idee dazu entstand, als ich im Garten eines Ferienhauses am Comer See, ein auf der Spitze stehendes fest montiertes Würfel-Gerippe sah, in desem Inneren sich ein leicht S-förmig gebogenes, vom Wind bewegtes Blech (wie als Blickfang vor Tankstellen häufig zu sehen) drehte. Ich frug mich, welche Kontur es haben müsste, wenn es den verfügbaren Raum im Würfel ganz ausfüllen würde. Als ich einen an einem Faden aufgehängten Würfel rotieren ließ, sah ich schnell, was mir ein praktischer Mathematiker vermutlich sofort gesagt hätte: unten und oben dreieckig (auch von mir leicht vorhergesagt), im mittleren Drittel von zwei Hyperbeln begrenzt (Rotations-Hyperboloid als Rotationsfigur). Aber: warum sollte mein Wind-Rad nicht der drehende Würfel selbst sein?

<< Abb.1 Eine Plastik-Flasche als Windrad
<< Abb.2 Savonius-Rotor, [www.energyprofi.com, Der Savonius-Rotor]

Zuerst meinte ich, dem Würfel Flügel aufsetzen zu müssen oder solche mit herausgebogenen Wand-Teilen zu formen, wie ich das vorher mit einer Plastik-Flasche (Abb.1) ausprobiert hatte. Ein Versuch zeigte, dass der Würfel auch mit nach innen gebogenen Wand-Teilen im Wind drehte. Bei der Suche nach der Erklärung stieß ich auf den Savonius-Rotor (Abb.2). Mein Wind-Würfel ist zwar ein viel stärker geschlossener Hohlraum und hat keine deutlich geformrte Schaufeln, ich stelle mir aber vor, dass beide nach dem gleichen Prinzip (und mit gleich schlechtem energetischen Wirkungsgrad) funktionieren.

Die Aufnahmen für die Kugellager sind diagonal gebohrte Würfelstücke. Zum Bohren auf der Drehbank wurden sie in einem Dreibacken-Drehbank-Futter auf drei der sechs Kanten gespannt, die beim Rotiernen als sogenannte Regelfläche ein Rotations-Hyperboloid bilden.

2. Drei-Würfel-Windrad   ↑ Anfang

Einen Körper aus Teilen herzustellen, die sich nur linien-haft berühren, war einerseits eine Herausforderung an die materielle Machbarkeit, führte bei der Drei-Würfel-Ecke aber auch zu einem interessanten Gebilde. Ich verwende sie in einem Würfel-Turm (s.dort 3.1), wobei die jeweils höhere Ecke die halbe Kantenlänge der unteren hat, und mit systematisch gefärbten Flächen als räumlichen "Farb-Kreis" und als Farb-Kreisel.

Schliesslich bemerkte ich, dass ich sie auf einer Spitze pendelnd rotieren lassen kann. Der Eckpunkt der nach unten offene Ecke iegt höher als der Schwerpunkt der Dreier-Kombination. Ich machte die drei Einzel-Würfel hohl. Drei Flächen jedes Würfels bestehen aus gelochtem, die anderen drei aus vollem Blech, so dass aerodynamisch ein ähnliches Gebilde wie das Schalenkreuzanemometer vorliegt (die gelochten Wände lassen sich wegdenken, da sie kaum als Luftwiderstand wirken).

Die Würfel-Kombination ist in der Innen-Ecke gelagert. Die drei Dreh-Freiheiten (Freiheitsgrad f=3) sind belassen, das zusätzliche Pendeln ist erwünscht. Das Windrad hat eine Pfanne, mit der es auf einer Spitze aufliegt (nur eine starke Windhose kann es abheben). Die Pfanne befindet sich im Innenring eines Kugellagers, denn ein Kugellager hat geringeren Dreh-Widerstand als ein Spitzenlager.

3. Drei-Würfel-Taschen-Windrad   ↑ Anfang

Dieses Windrad ist eine deutlichere Näherung an das Schalenkreuzanemometer (Abb.4). Die drei gelochten Wände jedes Einzelwürfels sind weggelassen, bei zwei von den drei vollen Wänden ist in der Diagonale die Hälfte abgeschnitten. Die Restfläche der Wände ist ein Drittel der ganzen Würfel. Das Windrad hat keine Teile mehr oberhalb der Lagerstelle, ist somit vorteilhaft an seiner höchsten Stelle gelagert. Der Wind muß sehr stark sein, bevor es bis zum Anschlagen an den Stab mit Lagerspitze auspendelt. Ich hielt aber diese Variante für zu wenig elegant und ließ es bei einem Papp-Modell bewenden.

↑ ↑ Abb.4 Schalenkreuzanemometer, im Gegenuhrzeigersinn drehend, [http://www.wind-energie.de/de/technik/skala/anemometer]

4. Drei-Dächer-Windrad   ↑ Anfang

Ich habe diese Variante aus dem oben genannten Papp-Modell entwickelt, indem ich die Taschen abdeckte und deren zwei unteren Rest-Wände entfernte (Abb.5). Auf diese Weise sind drei schiefe Dächer entstanden, deren horizontalen Firste sich in der Mitte über der Lagerstelle treffen. Pro Würfel ist eine von sechs Wänden übrig geblieben (zwei halbe dreieckige Wandstücke). Dazugekommenen ist ein gleichseitiges Dreieck, das die Tasche (= Wüefelecke) abdeckt (58% einer ganzen Wand).

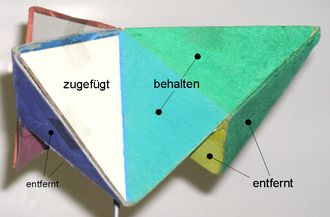<< Abb.5 Vom Drei-Würfel-Taschen-Windrad zum Drei-Dächer-Windrad

Die eben gemachte nicht leicht verständliche Beschreibung geht konform damit, dass in dieser Variante die drei Würfel, von denen ausgegangen wurde, kaum noch erkennbar sind. Stärker ist der Eindruck, dass drei schiefe Dächer aneinander gehängt sind. Vom Treffpunkt ihrer Firste verlaufen drei Rinnen nach unten. Die Flächen beidseits einer Rinne sind nicht gleich groß und nicht gleich steil. Diese Unsymmetrie ist Ursache dafür, dass der anströmende Wind links der Achse den größeren Widerstand findet und das Windrad im Uhrzeigersinn (von oben gesehen) dreht.

<< Abb.6 Drei-Dächer-Windrad, Untersicht

Ein anderer Eindruck ist, dass ein sechsfach im Zick-Zack geknicktes Band im Kreis herum geführt ist. Gegenstücke der drei Rinnen sind drei auf der Unterseite vorstehende Kanten (Abb.6). An deren unteren Enden ist ein Ring angesetzt, der dafür sorgt, dass das Windrad bei äußerster Schräglage einen gleichmäßigen Anschlag findet. Falls sich bei starkem Sturm die Spitzenlagerung löst, umschließt dieser Ring weiter den Spitzenstab, so dass das Windrad nicht herunterfallen kann.

5. Vier-Würfel-Windrad   ↑ Anfang

Vier Würfel über je zwei Kanten miteinander verbunden, deren umschließender Würfel doppelte Kantenlänge und doppeltes Volumen (Ergänzung mit vier weiteren Würfeln in den leeren Ecken) hat, verwendete ich vor langer Zeit für ein Würfel-Arangement (s.dort 4.1), dessen vier leere Ecken je mit der nächst kleineren Vierer-Kombination gefüllt war. Das dadavon angeregte Windrad funktioniert wie zwei übereinander liegende Savonius-Rotoren. Zwei der vier vertikalen Wände der hohlen Würfel bestehen aus Lochblech. Die Deckflächen sind geschlossen, damit wenig Regenwasser eindringt, die Bodenflächen sind gelocht (im Prototyp wegen Lochblechmangel nur die der oberen Würfel), damit eingedrungenes Regenwasser abfließen kann. Vielleicht wäre die Wirkung des Windes besser, wenn auch die Deckflächen gelocht wären (Umlenkung der Luft anstatt Stau). Es ist aber auch so dasjenige meiner Windräder, dass bei aufkommenden Wind zuerst anfängt, sich zu drehen.

Siegfried Wetzel, CH 3400 Burgdorf, November 2010

 ↑↑ Anfang
<< Home
<< anderes Geometrisches