<< Home
<< andere Geomtrie-Beiträge
↓↓ Ende
Sonnen-Sektor, eine vielseitige Gartenplastik
(DGC-Jahresschrift 2006)Zusammenfassung
Vorgestellt wird eine kugelförmige Plastik, in der das geozentrische Weltbild enthalten ist. Sie zeigt den sich täglich und jährlich ändernden Sonnenstand auf der durch den Horizont begrenzten Himmelssphäre an. Somit kann sie dem Sonnenuhrenfreund als anschaulicher Merkzettel, der die Bewegung der Sonne zum Inhalt hat, dienen. Bei entsprechender Skalierung funktioniert sie auch wie eine übliche Kugelsonnenuhr. Fasst man sie als Erdkugel auf, so ist deren sich ändernde Besonnung - insbesondere am Pol - zu erkennen. Sie ist generell eine gute Vorstellungshilfe bei gnomonischen Betrachtungen und Berechnungen, z.B. mit Hilfe der sphärischen Trigonometrie. Einige Beispiele werden erwähnt. Der vorliegende Artikel enthält auch Bemerkungen zur Konstruktion und Herstellung dieses kugelförmigen Gebildes. Aus der dazu verwendeten Kugelschale wurde anschliessend eine Skaphen-Sonnenuhr angefertigt.
Inhalt
1. Einleitung2. Die Vielseitigkeit der Plastik
3. Anfertigung aus Metall
4. Metallrest-Verarbeitung zu einer Skaphe
5. Anfertigung aus Marmor-Beton
6. Ein Himmel für die Skaphe
7. Literatur
1. Einleitung ↑ Anfang
Bereits am Beginn meines Interesses an Sonnenuhren entwarf ich diese Plastik (Abb.1) und habe sie damals in den "Schriften der Freunde Alter Uhren" vorgestellt [1] und in der folgenden "Jahresschrift" nochmals abgebildet und wieder als Erklärungshilfe benutzt [2].

Abb.1 Sonnen-Sektor als Modell
mit Sonne, Äquatorebene und Mittags-Stundenebene >>
Damals handelte es sich noch um ein kleines Modell aus Polystyrol. Inzwischen habe ich die Plastik für den Garten zweimal angefertigt und mit den Metallresten der einen Ausführung eine Sonnenuhren-Skaphe gebaut. Nach einer zusammenfassenden Darstellung der Vielseitigkeit der Plastik zeige ich Bilder dieser grösseren Objekte und erwähne einiges vom Drumherum.
2. Kurze Zusammenfassung der vielseitigen Verwendungsmöglichkeit der Plastik ↑ Anfang
Die Plastik erwies sich mit der Zeit als vielseitiger - vor allem, nachdem sie vergrössert im Garten stand - als ich am Anfang dachte und wollte. Auch deshalb komme ich nochmals auf sie zurück, wobei ich jetzt zwischen mit ihr möglichen qualitativen und quantitativen Aussagen unterscheide, je nachdem, ob etwas nur prinzipiell erkennbar wird, oder ob mit ihr Messungen möglich sind.
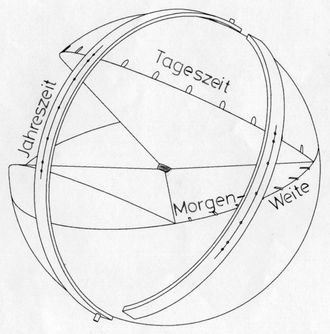
Abb.2 Sonnensektor mit drehbarem
Lineal und Skalen für Stunden und Morgenweite >>
Qualitative Aussagen:
- Der Himmel kann als eine sich über dem Horizont wölbende Sphäre gedacht werden. Unter dem Horizont befindet sich ihr Gegenstück, von dem wir nichts wissen, in das wir nicht hineinschauen können.
- Das Himmelsstück (Sektor), in dem sich die Sonne befinden kann, ist begrenzt.
- Ihre tägliche Bewegung findet auf einem Klein-Kreis statt. Der Sonnenstrahl zum Beobachter ist Mantellinie eines Kegels.
- Wenn die Sonne ihren täglichen höchsten Punkt passiert, ist sie momentan im Süden.
- Im Sommer "steht" die Sonne höher als im Winter, geht früher/später und nördlicher (positive anstatt negative Morgen-/Abendweite) auf/unter.
- Trotz Unterschieden übers Jahr befindet sich die Sonne zur gleichen Stunde (WOZ) immer in derselben Ebene (Stundenebene).
- Der Kegel degeneriert an den Äquinoktialtagen zu einer Ebene in der Mitte (Ebene des Himmels-Äquators), die mit dem Horizont den Winkel (90°-φ) (φ = geographische Breite des Aufstellortes) bildet.
Die Sonnenbahn beginnt genau im Osten, endet genau im Westen und ist genau ein Halbkreis (deshalb genau 12 Stunden lang), unabhängig vom Winkel φ. - Die gemeinsame Achse aller täglichen Kreisbahnen zeigt zum Himmels-Nordpol (wenn φ > 0) und schneidet den Horizont unter φ.

Abb.3 Erd-Modell
Tag-Nacht-Grenze an einem Äquinoktial-Tag >>
Quantitative Aussagen
- In die Plastik sind einige Konstanten fix eingebaut:
geographische Breite φ= 47° für Bern,
Grenzwert der Sonnen-Deklination δgrenz = ± 23,5°. - Davon sind abhängig und ebenso fix:
die Tageslänge an den Sonnenwendtagen: 15,7h (SSW) und 8,3h (WSW),
die Mittagshöhe: 66,5°(SSW) und 19,5°(WSW),
die Morgen-/Abendweite: ±35,8° . - Die Plastik lässt sich auch skalieren:
mit der Tageszeit z.B. beim oberen Klein-Kreis,
mit der Morgen- und/oder Abendweite z.B. an einem Horizont-Rand.
Dazu käme ein um die Himmels-Achse drehbares, kreisförmig gebogenes durchsichtiges Lineal. Seine Skala enthält die Jahreszeit. In Abbildung 2 ist diese mögliche Erweiterung zu sehen. - Die Tageszeit wird abgelesen, wenn die skalierte Linie des Lineals als mittiger Schatten auf der zentralen Kugel liegt. Als Datum gilt derjenige Skalenstrich, der diese Kugel auch mittig beschattet.
- Der Zeitpunkt des Sonnenauf- bzw. -untergangs lässt sich ermitteln, wenn man das Lineal bis zum entsprechenden Horizont-Rand dreht. Zur gültigen Zeit kreuzt das Lineal mit dem vorher bestimmten Datumsstrich diesen Rand. Am Rand selbst wird die Morgen-/Abendweite abgelesen.
- Die Kugelform der Plastik lässt diese auch als Modell der Erde, deren Achse richtig im All ausgerichtet ist, ansehen:
Die Koordinaten des Subsolaren Punkts entsprechen den abgelesenen Werten der Tageszeit (geographische Länge) und des Datums (geographische Breite). - Die über die Kugeloberfläche wandernde Grenze zwischen Licht und Schatten ist die Grenze zwischen Tag und Nacht auf der Erde. Schön ist zu sehen, wie die Gegend nördlich des Polarkreises im Sommer 24 Stunden Tag, im Winter hingegen dauernd Nacht haben kann.
Abbildung 3 ist an einem Äquinoktialtag aufgenommen. Man könnte den Polarkreis und noch einige nördlichere Breitenkreise auftragen und so mittels der einen solchen Kreis tangierenden Licht/Schatten-Grenze auch auf diese Weise das Datum im Sommerhalbjahr ablesen (s. Fotomontage in Abb.3).

Abb.4 Sonnen-Sektor aus Metall
und Kunststoff auf einem winterlichen Friedhof >>
3. Anfertigung aus Metall ↑ Anfang
Wie jede Metallplastik war auch mein Sonnen-Sektor aus Gewichtsgründen hohl. Ich konnte zufällig zwei Halbkugeln aus Blech ( Durchmesser 660 mm, Blechdicke 3 mm) preiswert erwerben, die ein Kunstschmied nicht mehr benötigte. Damit war das Wichtigste beschafft. Ein ebenes Blech für den Horizont war auch keine Preisfrage, wohl aber der relativ grosse "Lampenschirm" mit Spitzenwinkel "133° (180°-2δgrenz) für die Kegel. Ich scheute die Kosten einer Einzelanfertigung und wich auf PVC-Folie (Dicke 1 mm) aus. Damit hatte ich mir aber das Verbindungsproblem der Folie mit dem Metall (Eisen) geschaffen, besonders entlang der (Klein-)Kreise. Schweissen zwischen Eisen und Eisen wäre einfacher gewesen. Ich schraubte die Teile mit Hilfe etlicher sich im Inneren befindender Winkel zusammen, was natürlich keine wasserdichte Verbindung war. Das Zentrum war eine kleine Messing-Kugel mit (Kleinstkreis-)Schlitzen zum Halten der Folien-Kegelspitzen.
Diese Plastik gab ich ein Winterhalbjahr lang in eine Ausstellung für Grabmalkunst (Abb.4), wobei ich auf den Begleitzettel schrieb, dass anstatt des sektorförmigen Ausschnitts auch ein Kegelschlitz, durch den (nur) an einem bestimmten Tage die Sonne die Kugelmitte erreicht, möglich sei. Derart könnte auf einen wichtigen Tag im Leben des Betroffenen hingewiesen werden, wie das sinngemäss auch Zenkert [3] durch Verwendung einer Datumslinie auf einer Sonnenuhr vorschlägt.
Als ich die Plastik später aus Marmor-Beton fertigte, nahm ich die Metall/Kunststoff-Version wieder auseinander.

Abb.5 Sonnenuhren-Skaphe
identisch mit im Sonnen-Sektor fehlendem Stück >>
4. Metallrest-Verarbeitung zu einer Skaphe ↑ Anfang
Vorerst hatte ich aber nur den Metallrest von der oberen Halbkugel, der bei deren Zersägen entlang der zwei den Sektor begrenzenden Kleinkreise anfiel. Der Sektor ist entgegen dem Namen der Plastik der Abfall. Gebraucht sind die beiden Seitenteile.
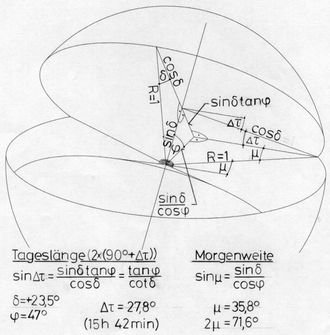
Abb.6 Berechnung
der Tageslänge und der Morgen-/Abend-Weite >>
Dieser Rest ist aber eine Skaphe minimaler Ausdehnung, die ich zu einer solchen Sonnenuhr verarbeitete (Abb.5). Auf der Kugelinnenfläche brachte ich die Skala für Wahre Ortszeit (WOZ) und die Datumslinie der Äquinoktialtage an. Weitere Datumslinien sind als Parallelen zu letzterer denkbar. Als Schattenwerfer gebrauchte ich eine kleine Messing-Kugel, die ich mit Drähten zwischen die diagonalen Ecken der Skaphe spannte.
Während dieser Arbeit beschäftigte mich die Frage, welchen Winkel die beiden Drähte untereinander einnehmen, was mit der Bogenlänge der beiden Grosskreisränder, die auch die maximale Morgen-/Abendweite angeben, beantwortet wird. Dazu kam die Frage, wie lang eigentlich die beiden Kleinkreisränder der Skaphe, die ein Mass der Tageslänge an den Sonnenwend-Tagen sind, seien.

Abb.7 Sonnen-Sektor aus Marmor-Beton >>
Zu den zur Rechnung nötigen Bildern ist mit der Plastik als Anschauungshilfe leicht zu finden (Abb.6, inkl. Rechnungen).
Ein weiterer Gedanke war:
Der Grenzfall für die Vergrösserung beider Winkel in höheren Breiten ist in den Rechenergebnissen "mit besprochen". Er tritt ein, wenn deren Sinus zu 1 wird. Die Winkel sind 90° geworden, mehr geht nicht. Die Auflösung der Gleichungen nach φ ergibt das Komplement von δ zu 90°, also φ=90°-δ . Bei grösseren Werten sind die Gleichungen ungültig ("error"). In der physikalischen Welt bedeutet diese Aussage, dass bei φ=90°-δ die maximale Tageslänge von 24 Stunden erreicht ist, und die Sonne den Horizont im Norden zu Mitternacht nur berührt. Bei δ=+23.5° (SSW) ist das am nördlichen Polarkreis der Fall.
5. Anfertigung aus Marmor-Beton ↑ Anfang
Grabmale aus Blech sind unerwünscht, Stein ist der bevorzugte Werkstoff. Aber auch für meinen Garten suchte ich nach einem dauerhafteren Werkstoff und nach wetterfesterer Art der Ausführung. Die Arbeit als Steinbildhauer behagte mir nicht. Ich wollte Steinguss herstellen, wie es die Natur selbst tut. Das hiess Betonieren unter Verwendung einer Schalung, die die gewünschte Form gewährleistet. Ein heller und natürlich aussehender Beton lässt sich mit handelsüblichem weissen Zement und hellem Füllstoffen, wie Marmorsand und -kies gewinnen. Abbildung 7 zeigt das Ergebnis.
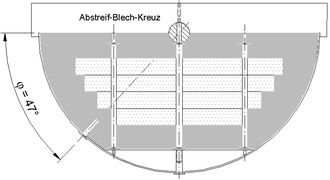
Abb.8 Herstellung der unteren Beton-Halbkugel >>
Die nun verfügbare untere Metall-Halbkugel wurde mit dieser Mischung ganz gefüllt, was die untere Hälfte der Plastik erbrachte. Zur Gewichtsminderung wurde aber im Inneren Polystyrol eingelegt. Ein kleiner unterster Kalotten-Teil wurde weggelassen, um eine Aufstell-Fläche zu gewinnen (Abb.8).
In derselben Halbkugel wurden auch die beiden oberen Teile gegossen. Dafür ist folgende vorgängige Feststellung wichtig:
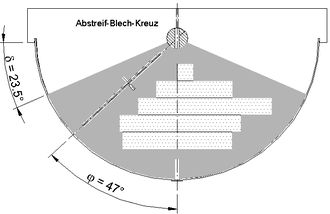
Abb.9 Herstellung der beiden oberen Beton-Teile >>
Beide Teile bilden zusammengesetzt einen einzigen Rotationskörper. Das ist eine Kugelkalotte (hku = R(1-sinδgrenz)) mit aufgesetztem Kegel (hke = R sinδgrenz) oder als Ganzes ein Kugelausschnitt (Kugelradius R = hku + hke). Die Kegelfläche formte ich mit Hilfe einer um die Kugelausschnitt-Achse rotierenden, durch den Mittelpunkt führenden und um den Winkel δgrenz geneigten Blechkante (Abb.9). Die Trennfläche zwischen beiden Teilen hat mit der Achse den Winkel φ (, d.h. bei einer Plastik für einen Ort nördlich des Polarkreises wäre das Oberteil einteilig und stünde auf seiner Spitze).

Abb.10 Skaphe mit Himmel, von Osten >>
Mit einem trennenden Einlegeblech erhielt ich die beiden Teile sofort einzeln. Polystyrolstücke wurden ebenfalls eingelegt. Eine Mittenkugel (blaue Murmel) war wie schon beim Giessen des Unterteils auch dabei, um den für sie später benötigten Hohlraum zu schaffen.
Nach dem Transport zum Aufstellplatz wurden alle Teile mit Klebstoff dauerhaft zusammengefügt.
6. Ein Himmel für die Skaphe ↑ Anfang
Nach Demontage der Metall-Plastik (s. Abschnitte 3 und 5) wurden auch die beiden Oberteile für eine allfällige andere Verwendung wieder frei. Die PVC-Kegelmäntel warf ich weg und montierte die beiden Metall-Teile (jederzeit abnehmbar) auf die Skaphe (s. Abschnitt 4) und erhielt eine etwas skurril anmutende Sonnenuhr (Abb.10). Mit ihr kann ich aber einige in der Plastik allgemein enthaltene Zusammenhänge konkreter zeigen:
Die Skaphe funktioniert immer (am Tage bei Sonnenschein) trotz teilweiser Abschirmung des Himmels. Der Grenzfall ist in Abb.11 zu erkennen, wo der Schatten des grösseren Himmels-Teiles die kleine Kugel in ihrer Mitte trifft und den unteren Rand der Skaphe tangiert. Es ist der Tag der Sommersonnenwende.

Abb.11 Skaphe mit Himmel, von Süden >>
Beim Betrachten dieser Montierung stellte sich mir wieder eine Frage, nämlich unter welchem Winkel eigentlich die Sonne auf- bzw. untergeht, insbesondere an den Sonnenwendtagen. Der in Abbildung 10 gesehene Winkel zwischen Horizont und dem rechten Himmels-Teil ist ca. 90°-φ. Der gesuchte Winkel ist kleiner, man sähe ihn auf einem Foto, das von weiter rechts aufgenommen wäre. Die Uhrenmitte befände sich im Scheitel des fraglichen Winkels.
Aber wir wollen es sowieso genauer wissen und stellen eine Rechnung an, für die die anschauliche Hilfe vor uns steht und für die wir zusätzlich Abbildung 12 (inklusive Rechnung) verwenden:
Die vorher (Abschnitt 4) gestellten Fragen waren mit ebener Trigonometrie zu beantworten. Jetzt benutzte ich ein sphärisches Dreieck, dessen eine Ecke am Ort des Sonnenaufgangs liegt. Die Sonnenbahn ist ein Kleinkreis und gehört deshalb nicht zum Dreieck, sie wird aber vom Grosskreis ihres Stundenwinkels rechtwinklig geschnitten, so dass der fragliche Winkel dennoch zu gewinnen ist.
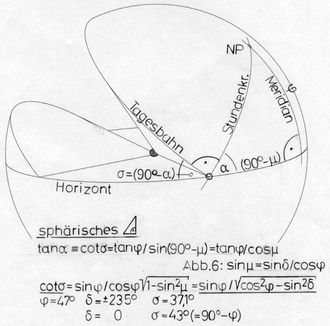
Abb.12 Berechnung
des Bahnwinkels bei Sonnenauf- und -untergang >>
7. Literatur: ↑ Anfang
[1] S.Wetzel: "Die Physik der Sonnenuhr", Schriften der "Freunde alter Uhren", 1998
[2] S.Wetzel: "Mathematik und Sonnenuhr", DGC-Jahresschrift 1999
[3] A.Zenkert: "Faszination Sonnenuhr", Frankfurt, 2002
![]() Siegfried Wetzel, CH 3400 Burgdorf, Januar 2008 (Jan.20)
Siegfried Wetzel, CH 3400 Burgdorf, Januar 2008 (Jan.20)
<< andere Geomtrie-Beiträge
Druck-Version (2-spaltig, 6 Seiten, *.pdf, 2.45 mB) >>
<< Home