<< Home
<< andere Geometrie-Beiträge
 ↓↓ Ende

Kegel-Sonnenuhr

Inhalt

1. Einleitung
2. Modell der Himmelssphäre
3. Schattenwerfer in der Sonnenaufgangs - bzw. in der Sonnenuntergangs-Ebene
4. Die Tagesbahn des Schattenwerfers, Kegel als Schattenwerfer
5. Berechnung der Stundenlinien auf dem Zifferblatt
6. Literatur und Bildnachweis

1. Einleitung  ↑ Anfang

Im Sonnenuhrenpark von Genk in Belgien liegt ein mit seiner Spitze nach Süden zeigender Metall-Trichter am Boden (Abb.1), dessen Schatten auf seiner östlichen Seite Babylonische (Abb.3), auf seiner westlichen Seite Italienische Stunden (Abb.4) anzeigt. Als Sonnenuhren-"Zeiger" dienen die beiden Schatten-Kanten des Kegel-Mantels.

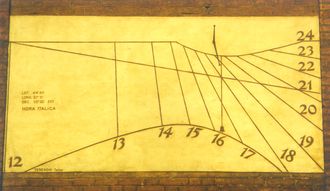
Abb.1   (links): Kegel-Sonnenuhr in Genk /Belgien, Blick von Norden, Randdurchmesser 3,7 m
Abb.2 (rechts): Italienische Stunden auf einer Wand-Sonnenuhr mit Nodus (Punkt-förmiger Schattenwerfer), knapp 19 Stunden nach gestrigem Sonnenuntergang (kurz vor Wahrem Mittag, im Oktober in Asti/Italien)

Abb.3   (links): Babylonische Zeit: 9:15 (östl. Skala) [1], 9 ¼ Stunden seit Sonnenaufgang
Abb.4 (rechts): Italienische Zeit:14:15 (westl. Skala) [1], 14 ¼ Stunden seit gestrigem Sonnenuntergang

<< Abb.5 Modell der Himmelssphäre aus mehreren gegeneinander drehbaren Teilen

Babylonische und Italienische Stunden haben einen von der Jahreszeit abhängigen Beginn ihrer Zählung, den Sonnenaufgang bzw. den Sonnenuntergang. Bisher war keine Möglichkeit bekannt, sie mit einem linienförmigen Schatten oder einer linienförmigen Schattenkante anzuzeigen. Alle Sonnenuhren, deren Anzeige von der Jahreszeit abgängig ist, verwenden einen Schatten-werfenden Punkt, so auch die bisher bekannten Sonnenuhren für zum Beispiel Italienische Stunden (Abb.2).

Die überraschende Lösung dieser vom Spanier Javier Moreno Bores erfundenen [2] und in Genk aufgestellten Kegel-Sonnenuhr wird mit Hilfe eines Modells (Abb.5), das die Bewegung der Sonne an der Himmelssphäre nachbildet, erklärt.

2. Modell der Himmelssphäre (siehe Abb.5)  ↑ Anfang

von innen nach außen:

(1) Horizont-Ebene (waagerecht gestellt)
(2) transparenter Ring als Sonnenaufgangs-Ebene, links (rechts für Sonnenuntergang); Null-Lage: waagerecht;
     getragen von einem massiven Ring (Fahrradfelge 26'')
(3) Stunden-Ebenen-Bügel
(4) massiver Ring (Fahrradfelge 28'') als Meridian und Gestell; Teile (1) bis (3) um Himmels-Achse drehbar

3. Schattenwerfer in der Sonnenaufgangs - bzw. in der Sonnenuntergangs-Ebene  ↑ Anfang

Die Anzeige der Tageszeit (bezogen auf den Wahren Mittag) einer Polstab-Sonnenuhr ist von der Jahreszeit unabhängig, weil sich der Polstab immer in der Stundenebene der Sonne befindet, sowohl zu jeder Jahreszeit als auch zu jeder Tageszeit.

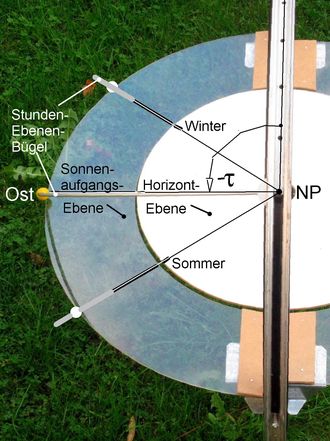
<< Abb.6 Horizont- und Sonnenaufgangs-Ebene, Schräg-Blick vom Himmels-Nordpoll NP aus

Die Sonnenaufgangs-Ebene ist bei Sonnenaufgang identisch mit der Horizont-Ebene (alle folgenden Aussagen lassen sich leicht für den Sonnenuntergang und Italienische Stunden abwandeln). Im Modell ist es die östliche Hälfte eines transparenten Rings, der die Horizont-Scheibe umschließt (links in Abb.5). Sie wird (mangels eines gängigen Begriffs) auch nach Sonnenaufgang als Sonnenaufgangs-Ebene bezeichnet. In Abb.6 ist gezeigt, dass der Stundenwinkel τ bei Sonnen-Aufgang übers Jahr verschieden ist. Der die Stunden-Ebene repräsentierende Halbkreis-Bügel nimmt verschiedene Winkel-Positionen ein.

Die horizontale Lage der Sonnenaufgangs-Ebene kennzeichnet den Beginn (Nullpunkt) der Babylonischen Stunden-Zählung (in äquinoktialen Stunden). Die Ebene dreht sich (mit der Sonne) während des Tages 15° pro Babylonische Stunde durch den Himmel um dessen Achse. Der ab Sonnenaufgang gezählte Stundenwinkel wird zur Unterscheidung vom üblichen Stundenwinkel τ mit Δτ bezeichnet.

Analog zum sonst üblichen Polstab wird ein linienförmiger Schattenwerfer, der sich sowohl zu jeder Jahreszeit als auch zu jeder Tageszeit in der Sonnenaufgangs-Ebene befindet, gesucht. Da er nicht unter den Horizont tauchen darf, kommt nur eine Richtung in Frage: Er zeigt in der Null-Lage der Ebene zum Nord-Punkt des Horizonts. Im Modell wird er von einem zwischen Zentrum und Ring-Innenkante gespannten Faden dargestellt (s. Abb.5).

4. Die Tagesbahn des Schattenwerfers, Kegel als Schattenwerfer  ↑ Anfang

Der zum Himmelspol NP zeigende Schattenwerfer in der Stunden-Ebene dreht sich über Tag nur um seine eigene Achse. Anwendbar ist hier ein einziger Stab, der Polstab.

Hingegen bildet der linienförmige Schattenwerfer in der Sonnenaufgangs-Ebene über Tag den Mantel eines Kegels. Eine Mantel-Linie dieses Kegels ist folglich zu einer bestimmten Babylonischen Stunde als linienförmiger Schattenwerfer einer Sonnenuhr für Babylonische Stunden zu gebrauchen. In der praktischen Ausführung zeigt der Schatten-Rand eines körperlichen Kegels diese Stunden an (Abb.7). Die Sonne streift den Kegel zu jeder Babylonischen Stunde bei einer anderen Mantellinie. Schattenwerfer ist ein Halb-Stab (ein in der technischen Optik gebräuchlicher Begriff, dessen Pendant der Halb-Spalt ist).

Abb.7 Kegel-Mantel als Tagesbahn eines linienförmigen Schattenwerfers in der Sonnenaufgangs-Ebene; Kegel-Körper als Schattenwerfer (Halb-Stab) für Babylonische (rechts) und Italienische Stunden (links)

5. Berechnung der Stundenlinien auf dem Zifferblatt  ↑ Anfang

Die Berechnung erfolgt mit Hilfe von sphärischen Dreiecken, die am Modell sichtbar gemacht werden können.

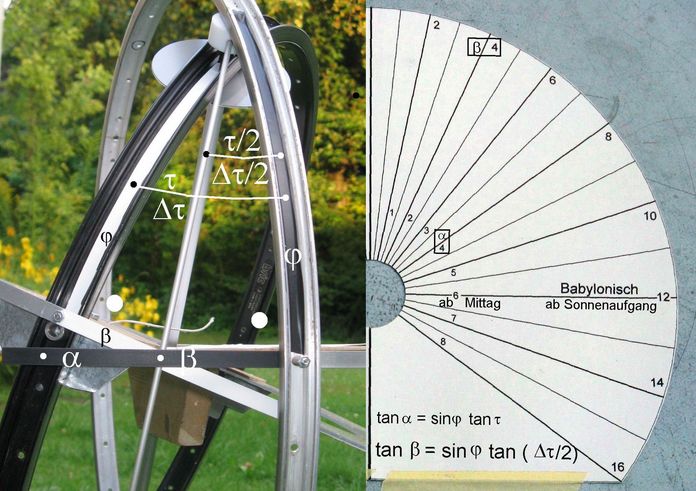Abb.8 Sphärische Dreiecke (links) zur Herleitung der Gleichung für die Stundenlinien einer Kegelsonnenuhr für Babylonische Stunden (rechts)

tan ß = sin φ · tan (Δτ/2)   (1).

Es bleibt noch zu zeigen, warum in diese Gleichung für den Winkel der Stundenlinien nicht der Stundenwinkel Δτ der Sonnenaufgangs-Ebene, sondern genau seine Hälfte Δτ/2 eingeht: Die Sonnenaufgangs-Ebene hat sich seit Sonnenaufgang um den Winkel Δτ verdreht, der durch zwei spiegelbildlich gleiche Dreiecke mit der gesuchten kurzen Kathete ß halbiert wird. Beide rechtwinkligen Dreiecke haben nämlich je eine gleich lange große Kathete (Bogen φ).

Die Gleichung für die Stundenlinien α einer horizontalen Polstab-Sonnenuhr unterscheidet sich vom Ergebnis nur dadurch, dass sie den unhalbierten Stundenwinkel τ enthält. Sie lautet:

tan α = sin φ · tan τ   (2).

Auch sie ist am Modell erkennbar: Als Polstab dient die Himmels-Achse. Sein Schatten fällt dort auf den Horizont, wo er von der Stunden-Ebene, die den Polstab enthält, geschnitten wird. Vom entsprechenden rechtwinkligen sphärischen Dreieck mit α sind der spitze Winkel τ = Δτ (τ aber ab Mittag gemessen) und die Seite φ bekannt. Gleichung (2) ist die Standardgleichung für das jetzt größere (ß → α) rechtwinklige Dreieck.

Folgerichtig gilt:
Die Stundenlinie für den doppelten Wert der Babylonischen Stunde (ab Sonnenaufgang gezählt) ist identisch mit der Stundenlinie der "gewöhnlichen" Stunde (ab Mittag gezählt). Auf dem Zifferblatt in Abb.8, rechts ist beispielsweise der Schritt von der 4. Babylonischen Stunde {ß4} zur 4. "gewöhnlichen" Stunde am Nachmittag {α4} gezeigt.

6. Literatur und Bildnachweis  ↑ Anfang

[1] http://www.fransmaes.nl/genk/welcome-e.htm: UNofficial Website of the Sundial Park in Genk (Belgium), 9. Cone

[2] Javier Moreno Bores (Madrid): A new Famliy of Sundials with conical Gnomon (The Compendium, Vol. 5, Number 2, Juni 98)

Siegfried Wetzel, CH 3400 Burgdorf, Oktober 2009

 ↑↑ Anfang
<< andere Geometrie-Beiträge             Druck-Version (2-spaltig, 4 Seiten, *.pdf, 3 MB)  >>
<< Home