<< Home
<< andere Farbe-Beiträge

Durchs Prisma fotografiert
Goethes Blick durchs Prisma, fotografiert

mein Wikipedia-Eintrag: Kantenspektrum (von mir erstellter Artikel in meiner Version)

Zusammenfassung

Inhalt

1. Einleitung  ↑ Anfang

Bei einem Blick durch ein Prisma gegen ein Fenster seines Arbeitszimmers sah Goethe farbige Ränder an den Fenstersprossen. Für ihn war das das Schlüsselerlebnis dafür, dass Farben nicht durch Zerlegung des Lichtes, wie Newton postulierte, sondern durch Zusammenwirken von Licht und Finsternis entstünden [1]. Mit dieser Auffassung konnte er sich aber nicht durchsetzen.

<< Abb.1 Spektrum des Sonnenlichts,
das durch ein kleines Loch im Fensterladen und ein Prisma auf die gegenüberliegende Zimmer-Wand fällt

Dennoch wurde der den Physikern "erlaubte" Schritt im Zusammenhang mt Kantenspektren bis zum Bild im Auge bis heute nicht vorgenommenen. Selbst im Goethe-Nationalmuseum, dem ehemaligen Wohnhaus und "Farb-Labor" Goethes am Frauenplan in Weimar hat man in relativer Dunkelheit, nämlich unter der Treppe im Foyer den Projektionsschirm eines Spektralapparates aufgestellt, so dass "eine brillante Farberscheinung wahrgenommen werden kann, die jedoch kein Kanten-Spektrum ist, wie es Goethe vielleicht besser gefallen hätte" [3].

Absicht der vorliegenden Arbeit ist, ausgehend von einer Fotoserie eine umfassende, aber einfache physikalische Behandlung des Phänomens zu versuchen.

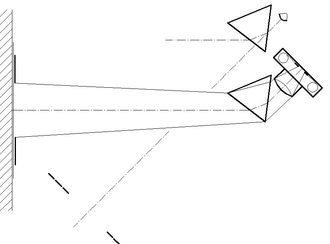
<< Abb.2 Blick und Fotografieren durch ein Prisma
(Spalt zwischen zwei schwarzen Streifen - Prisma - Auge/Fotoapparat)

2. Fotografieren durch ein Prisma
↑ Anfang

Die Rolle des Auges mit Linse und Netzhaut übernimmt ein Fotoapparat mit seinem Objektiv und dem Film. Auf diese Weise lassen sich die gesehenen Kanten-Spektren dokumentieren und kommunizieren.

Neben dem Blick auf einen Balken vor weißem Hintergrund (bei Goethe auf Fenstersprossen vor hellem Himmel) wird auch der Blick auf einen Spalt (weißer Streifen vor schwarzem Hintergrund) dokumentiert.

Balken und Spalt werden mit auf einer Hauswand übereinander befestigten geradkantigen schwarzen und weißen Papieren dargestellt. Der Fotoapparat ist davor aufgestellt. Ein waagerecht (parallel zu Balken bzw. Streifen) vor dessem Objektiv gehaltenes Prisma führt zu Bildern mit farbigen Streifen.

Daten:
Steifenlänge 21cm (DIN A4-Breite)
60°-Prisma (3 mal 53mm), Kronglas (n≈1,5), 63mm lang
Fotoobjektiv 1:4,5 f=70mm
24x36-Dia-Film ASA 100
Serien-Parameter ist die Streifenbreite.
Aufnahmen gegen besonnte Hauswand

3. Erhaltene Fotos (Foto-Serie)  ↑ Anfang

Die in analoger Form (1997!) gemachten Aufnahmen wurden digitalisiert (gescannt). Nebeneinander sind ohne und mit Prisma gemachte Fotos angeordnet. Die Bilder wurden rundum beschnitten (Reduktion der Breite auf ca.1/3). Die Farben blieben unverändert ausser der Reduktion der Farbtiefe auf 8 Bit/Pixel.

Von oben nach unten folgen sich Fotos, in denen sich die Breite des Spaltes (linke Hälfte) bzw. die Dicke des Balkens (rechte Hälfte) verkleinert (oben, breit: weiss bzw. schwarz zwischen den farbigen Kanten; Mitte, mittel: die farbigen Kanten berühren sich; unten, schmal: je eine neue Farbe ist entstanden).

Abb.3 Foto-Serie von Kanten-Spektren eines Spaltes (links) und eines Balkens (rechts)
daneben zum Vergleich die je ohne Prisma aufgenommenen schwarz-weissen Bilder

4. Diskussion der Fotos  ↑ Anfang

Bei der Diskussion der Kanten-Spektren werden die optischen Gesetze der Abbildung durch eine Sammellinse, der Dispersion des Lichts mittels Prisma und der additiven Farbmischung benutzt. Primäres Ziel ist, qualitative Aussagen zu gewinnen.

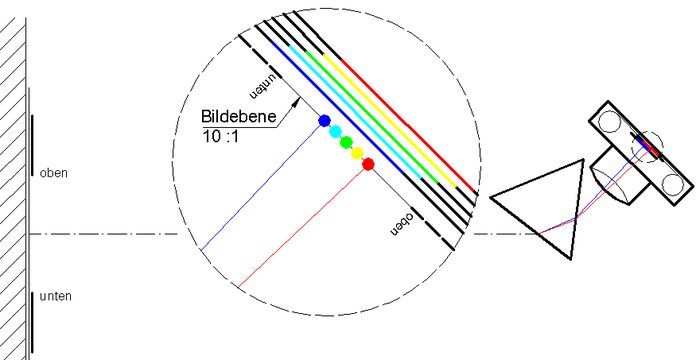
Abb.4 a) Zwischen Objekt und Bild sind oben und unten gegeneinander vertauscht.
          b) Ein weisser Punkt wird als Reihe farbiger Punkte abgebildet.
          c) Eine weisse Fläche (Spalt) wird als Stapel farbiger Flächen abgebildet.

Im Fotoapparat und auf der Netzhaut des Auges steht die Welt auf dem Kopf (Abbildung durch eine Sammellinse: Abb.4a). Die Bilder der fotografierten und der folgenden schematischen Kantenspektren sind im Kopfstand dargestellt, um das Verständnis für die Farbunterschiede an oberer und unterer Bild-Kante in Abhängigkeit von der Ablenkrichtung des Prismas nicht zu erschweren. Beim Blick durch das Prisma ist aber zu beachten, dass wir durch eine Leistung unseres Gehirns die Welt aufrecht sehen und dabei die vom Prisma bestimmte Anordnung der Farben vertauschen.

Betrachtet wird ein Schnitt durch die Spalte und Balken und durch ihre Bilder (alle benachbarten Schnitte sehen gleich aus). Von allen Punkten der weissen Unterlage gehen Lichtstrahlen aller Wellenlängen (Farben) des sichtbaren Lichts aus (Anmerkung 1). Im Prisma werden die Strahlen verschiedener Wellenlängen verschieden stark abgelenkt, die kurzwelligen Strahlen (Violett) stärker als die der langwelligen Strahlen (Rot) (Dispersion des Lichts mittels Prisma: Abb. 4b). Von den weissen Flächen entsteht eine Vielzahl vertikal gegeneinander versetzter verschieden farbiger Bilder (Abb.4c, Anmerkung 2). Da sie sich überlappen, addieren sie sich (additive Farbmischung) in einem großen Teil des Bildes zu Weiss. Nur an den Rändern (Kanten) bleiben farbige Reste übrig.

Die Schnitte durch Wand- und Bildebene sind in den folgenden Abbildungen mit einer endlichen Dicke dargestellt. Als Abbidungsmaßstab wird vereinfachend 1:1 angenommen. Spalt bzw. Balken befinden sich unten, darüber ein Stapel aus 5 farbigen Bildern, die zum Bild mit farbigen Kanten addiert sind, so wie sie vom Foto-Film bzw. von unserem Farbsinn wahrgenommen werden. Die 5 Farben sind die beiden Ränder des sichtbaren Spektrums (Rot und Violett) und die 3 Grund-Farben dazwischen. Das Spektrum enthält unendlich viele verschiedene Farben. Die prinzipielle Behandlung des Phänomens der farbigen Kanten erfordert die Reduktion auf eine begrenzte Zahl und ist mit 5 Farben möglich. Spalt bzw. Balken und Bild sind parallel übereinander gezeichnet. In Wirklichkeit werden die Lichtstrahlen zwischen beiden nach links abgelenkt, was mit einem Symbol angedeutet ist.

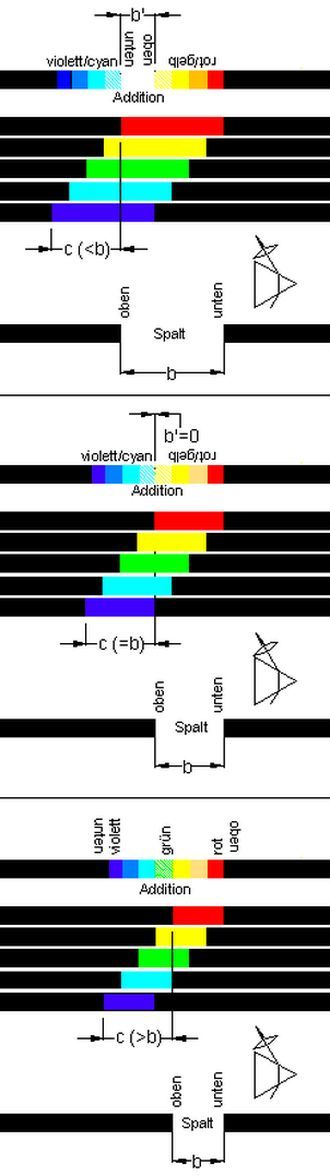
<< Abb.5 Kanten-Spektren eines Spaltes

4.1 Kantenspektren eines Spaltes   ↑ Anfang

Die Breite des Spaltes wird in den Teilbildern von oben nach unten kleiner. Vom Spalt geht weisses Licht aus, das im Prisma dispergiert. Die folgende Linse bildet ihn in zueinander versetzten Bildern in den ausgewählten 5 Farben (Abb.5) ab. In der Mitte, wo sich alle Einzelbilder überlappen ergibt die additive Farbmischung wieder Weiss. Nach aussen nimmt die Überlappung gestuft ab. Ganz aussen bleibt je 1 Farbe übrig, der untere Bild-Rand ist dort rot, der obere violett gefärbt. Zwischen der weissen Bild-Mitte und aussen addieren sich nur 4 bis 2 Farben. Die Summen sind helles Gelb, Gelb und Orange auf der roten Seite und helles Cyan, Cyan und Blau auf der violetten Seite, so wie es gemäss additiver Farbmischung zu erwarten ist. Die weisse Summen-Mitte ist schmaler als ein einzelnes Spalt-Bild
(b'< b).

In den mittleren Teilbildern ist der Spalt gerade so breit, dass die weisse Mitte in der Addition verschwindet. Die beiden farbigen Ränder sind noch gleich wie im ersten Teilbild.

Bei schmalerem Spalt (untere Teilbilder) überlappen sich auch in der Mitte nur noch 3 Farben, nämlich Gelb, Grün und Cyan (Abb.5). Die Addition aus Gelb und Cyan ist Weiss, ergibt aber zusammen mit Grün ein helles Grün als Gesamtergebnis. Dass Grün relativ hell ist, wird im Foto (Abb.3, links unten) nicht deutlich, weil das Bild wegen der Enge des Spaltes gesamthaft dunkler geworden ist. Man vergleiche in den Fotos die Abdunklung der Farben Rot und Violett zwischen breitem und engem Spalt. Kantenspektren wie in Abb.3, links unten werden als Newton-Spektren (Gegensatz: Goethe-Spektren, Abb.3, rechts unten, s.a. 4.2) bezeichnet [2].

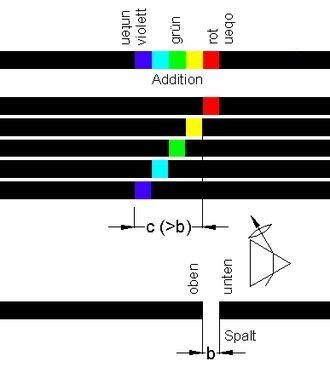
                                                                  Abb.6 >>
Kantenspektrum eines sehr engen Spaltes als Näherung an ein übliches, mit einem Spektrometer gewonnenes Spektrum

Abb.6 ist die Fortsetzung von Abb.5 zu sehr engem Spalt. Sie ist auf Abb.1 bzw. auf ein mit einem Spektrometer gewonnenes Spektrum anzuwenden. Zu erkennen ist die Tendenz, dass ein übliches Newton-Spektrum aus vielen Spaltbildern besteht, deren Farbe als monochromatisch bezeichnet werden kann. Dabei werden die Grenzen der Schematisierung in Abb. 5 und 6 sichtbar. Die Spektralbereiche für Gelb und Cyan sind in Wirklichkeit enger als die für Rot und Grün, und die aus dem Regenbogen bekannten Farben Orange und Blau treten hinzu. Die Farbe Violett dominiert (zusammen mit Blau) das Spektrum (ähnlich wie in Abb.1, Anmerkung 3).

Unser Auge besitzt zur Wahrnehmung von Licht unterschiedlicher Wellenlängen nur drei unterschiedliche Arten von Sensoren, die drei verschiedenen Zäpfchen-Typen, die für Violett, Grün und Rot maximal empfindlich sind. Bei breitem Spalt wird die Bild-Mitte von Licht aller wahrnehmbaren Wellenlängen getroffen. Die drei Zäpfchen-Typen sind gleich maximal gereizt, was wir als weiß interpretieren.

Es gibt eine mittlere Spalt-Breite, bei der in der Bildmitte das kurzwellige und das langwellige Licht im Gegensatz zum Licht mittlerer Wellenlängen schwächer zu werden beginnen, so dass nur noch die Grün-empfindlichen Zäpfchen maximal gereizt werden. Die Bildmitte wird farbig, nämlich grün. Zuerst ist der Weiss-Anteil noch hoch, bei sehr schmalem Spalt (Spektrometer in Dunkelkammer) tritt schliesslich reines Grün hervor. Die Stelle wird jetzt von Licht eines schmalen Wellenlängen-Bandes getroffen, das ausschliesslich die Grün-Zäpfchen reizt. Die anfängliche additive Farbmischung wird Schritt für Schritt zurück genommen, es wird entmischt.

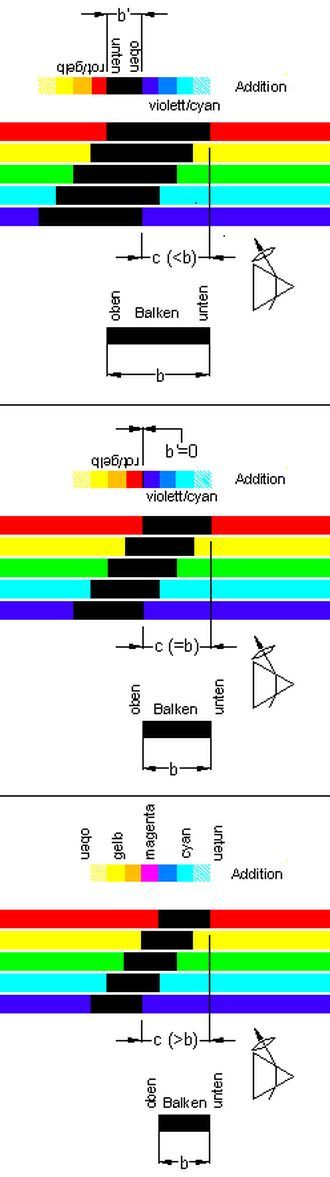
<< Abb.7 Kanten-Spektren eines Balkens

4.2 Kantenspektren eines Balkens  ↑ Anfang

Die Dicke des Balkens wird in den Teilbildern von oben nach unten kleiner. Von der Umgebung des Balkens geht weisses Licht aus, das im Prisma dispergiert. Die Linse erzeugt zueinander versetzte farbige Bilder (Abb.7). Weit aussen, wo sich alle Einzelbilder überlappen, entsteht wieder Weiss. Nach innen nimmt die Überlappung gestuft ab (4-fach bis 2-fach), bis ganz innen nur je 1 Farbe übrig bleibt: Rot oberhalb der schwarzen Bild-Lücke, Violett darunter. Die Zwischen-Summen sind helles Gelb, Gelb und Orange auf der roten Seite und helles Cyan, Cyan und Blau auf der violetten Seite. In der Summe ist die schwarze Lücke schmaler als beim Einzel-Bild (b' < b).

In den mittleren Teilbildern ist der Balken gerade so dick, dass die schwarze Lücke in der Addition verschwindet. Die beiden farbigen Außen-Bereiche sind noch gleich wie im ersten Teilbild.

Bei dünnerem Balken (untere Teilbilder) überlappen sich die inneren Ränder der farbigen Aussen-Bereiche. Violett und Rot addieren sich zu Magenta, das Goethe Pfirsischblüt nannte. Im Foto ist etwas Violett übrig geblieben, denn sein Anteil in den Säumen war grösser als der von Rot.

Kantenspektren wie in Abb.3, rechts unten werden als Goethe-Spektren bezeichnet [2]. Sie reichen nur von einem ungesättigtem Cyan über Violett und Magenta zu einem ungesättigtem Gelb, sie sind keine physikalische Kennzeichnung des sichtbaren Lichtes. Die Namensgebung ist lediglich eine Ehrerweisung der Goethe'aner an Goethe.

Die Addition von Violett und Rot zu Magenta erfolgt erst im Gehirn des Menschen. Voraus geht ihr die gleichzeitige Reizung der violett/blau- und der rot/orange-empfindlichen Netzhaut-Zäpfchen. Magenta ist heute wegen der Verwendung in Druckern eine "Standard-Farbe" geworden. Sie ist aber keine "physikalische Farbe", sie fehlt im "echten" Spektrum (Abb.1), also auch im Regenbogen. Ihr ist keine Wellenlänge zugeordnet, sie existiert nicht in unserer Aussenwelt.

Es existiert also eine Balken-Dicke, bei der die Bildmitte beginnt, von kurz- und langwelligem Licht getroffen zu werden. Gereizt werden zunächst nur die Violett/Blau- und die Rot/Orange-Zäpfchen, was als Magenta empfunden wird. Es findet eine additive Mischung statt. Bei sehr dünnem Balken haben sich schliesslich die beiden Kantenspektren so überlagert, dass sie sich gegenseitig zu Weiss ergänzen. Eine Situation, eine Bildstelle, wo ein schmales Wellenband die Grün-Zäpfchen allein reizt, tritt nicht auf. Wenn ihre Reizung beginnt, wird die Empfindung von Magenta zu Gunsten von Weiss lediglich schwächer. So wie ein sehr schmaler Balken bei direkter Betrachtung (oder durch ein Prisma bei monochromatischer Beleuchtung) nicht mehr erkennbar ist, erscheint er auch vor weissem Hintergrund nicht mehr in irgend einer Weise farbig.

Auch folgende Umkehr-Formulierung ist evident: So wie ein sehr schmaler Spalt vor einem Prisma ein sehr licht-schwaches Total-Spektrum der Lichtquelle erzeugt, führt ein sehr dünner Balken (oder ein weggelassener) wieder zur totalen Mischung des vom Prisma abgelenkten und aufgespaltenen Lichtes. Die von der Lichtquelle stammende grosse Helligkeit wird wieder erreicht. Der Grenzübergang beim Spalt lautet: Bei geschlossenem Spalt wird alles von der Lichtquelle stammende Licht ausgeblendet.

4.3. Spalt- und Balkenbreiten-Grenze, bei der die Bildmitte farbig zu werden beginnt
↑ Anfang

In der Technischen Optik sind quantitative Beziehungen formuliert, mit denen sich die im Versuch festgestellten Breiten-Grenzen kontrollieren lassen.

Der wellenlängenabhängige Brechungsindex wird mit empirisch gewonnenen Gleichungen aus Materialkonstanten, die der Hersteller ermittelt und publiziert, berechnet. Damit lässt sich die wellenlängenabhängige Ablenkung des Lichts mit einem Prisma (minimal bei symmetrischer Anordnung; weiterer Parameter: Winkel der brechenden Kante) bestimmen. Die unterschiedliche Ablenkung von Licht zweier verschiedener Wellenlängen sei die als Winkel bemessene Ablenkungsdifferenz.

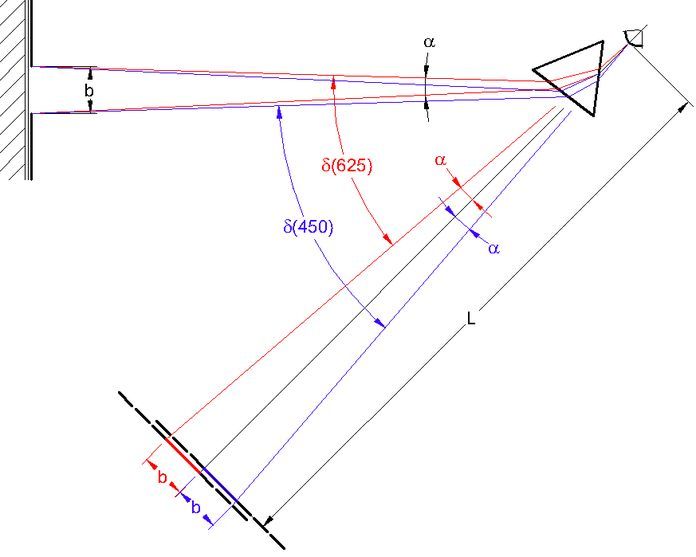Abb.8 Spaltbreiten-Grenze: Weiss verschwindet in der Bildmitte

Diese Ablenkungsdifferenz ist der Sehwinkel α, unter dem zwei farbige Bilder des Spaltes beim Blick durch ein Prisma versetzt erscheinen. Damit sie vereinzelt erscheinen (sich nicht überlagern), darf der Spalt eine gewisse Breite nicht überschreiten. Bei der zu ermittelnden Grenz-Breite handelt sich um das violett/blaue und das rot/orange Teilbild, die in der Bildmitte nur noch zusammen stossen, sich nicht mehr überlappen. Die zugehörigen Wellenlängen sind 450 nm (Violett/Blau) und 625 nm (Rot/Orange), die Empfindlichkeits-Maxima der zugehörenden Zäpfchen [4].

Das verwendete Prisma (Kantenwinkel γ=60°) besteht aus der Glassorte ZK7 (in einem Spektrometer-Versuch mit Quecksilber-Dampf-Lampe kontrolliert). Mit den vom Hersteller angegebenen Konstanten (inkl. Dispersions-Gleichung = Sedelmeier-Gleichung) [5] werden die Brechzahlen für die Wellenlängen 450 und 625 nm bestimmt:
n₄₅₀ = 1,5173 und n₆₂₅ = 1,5097.

Bei symmetrischem Licht-Durchgang gilt die Prismen-Formel
n_λ = sin (δ_λ+γ)/2) / sin (γ/2).
Sie erbringt aufgelöst nach δ_λ die beiden Ablenkwinkel δ₄₅₀ = 38,69° und δ₆₂₅ = 37,79°, bzw. die Ablenkungsdifferenz α = 0,90° (Sehwinkel).
Zwischen dem Winkel α, der Spalt-Breite b und dem Beobachtungsabstand L besteht die Beziehung α ≈ 180°/π · d/L.

Im Spalt-Versuch (Weiss verschwindet in der Bildmitte) ergab sich α ≈ 0,90° (b=26mm, L=1650mm).

5. Literatur  ↑ Anfang

[1] J.W. von Goethe: "Zur Farbenlehre", Tübingen, 1810 (oder ein Nachdruck)
[2] Maurice Martin: "Die Kontroverse um die Farbenlehre", Novalis, 1979
[3] Lutz Wenke u.a.: "Sonne und Wahrheit frei nach Goethe", Innovation 7, Carl Zeiss, 1999
[4] Harald Küppers: "Das Grundgesetz der Farbenlehre", Dumont, 1993, S.117, Abb.55
[5] Schott-Datenblatt für N-ZK7: http://refractiveindex.info/index.php?group=SCHOTT&material=N-ZK7

6. Anmerkungen  ↑ Anfang

<< andere Farbe-Beiträge             Druck-Version (2-spaltig, 8 Seiten, *.pdf, 210 KB)  >>
<< Home