<< Home
<< andere Fahrzeugtechnik-Beiträge

 ↓↓ Ende

Die Pendelachse am Auto

Inhalt

1. Einleitung  ↑ Anfang

Die Pendelachse war eine der ersten und einfachsten Einzelradaufhängungen an angetriebenen Automobil-Achsen. Sie wurde am häufigsten und sehr lange (bis zuletzt, d.h. bis 2002) als Hinterachse im Volkswagen-Käfer angewendet. Trotz bestmöglicher Milderung ihrer prinzipiellen technischen Nachteile in den 1950er-Jahren durch Mercedes-Benz beim Einbau in den W 120 verschwand ihre Anwendung fast ganz. Heute (2018/19) gibt es sie noch in den Lastwagen Tatra 815 und im 3-Rad-Kleintransporter Piaggio Ape.
Die Nachteile und ihre Milderung werden im folgenden beschrieben. Diese resultieren aus dem hoch liegenden Rollzentrum bzw. aus den hoch liegenden Gelenken, in denen die Halbachsen pendeln.

2. Eingelenk- und Zweigelenk-Pendelachse  ↑ Anfang

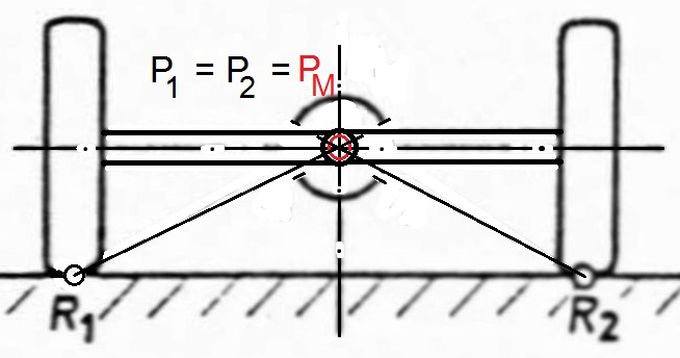
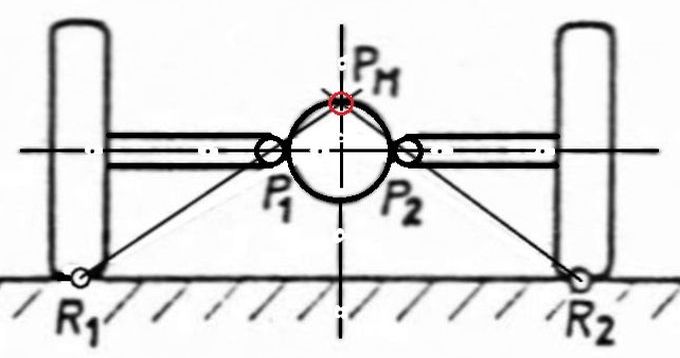Abb.1 Eingelenk-Pendelachse              R = Radaufstandspunkte, P = Halbachsen-Anlenkpunkte am Fahrzeugkörper,
Abb.2 Zweigelenk-Pendelachse; [1]    P_M = Wankzentrum (ein im Allgemeinen momentaner Punkt)

Die Eingelenk-Pendelachse (Abb.1) ist die historisch ältere. 1903 erwarb Edmund Rumpler auf sie ein Patent (Abb.3), und 1921 hat er sie erstmals in seinem Tropfenwagen angewendet.

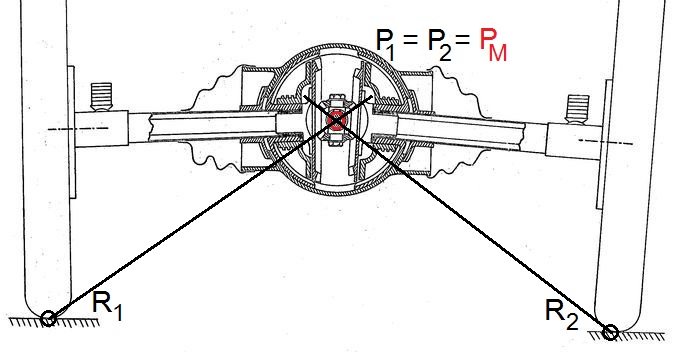Abb.3 Eingelenk-Pendelachse nach Rumpler.
          1. Abb. aus dem US-Patent #1514862
          Die beiden Halbachsen drehen sich um eine
          horizontale, durch den Mittelpunkt des
          Differential-Getriebes führende Achse.

Rumplers Lösung, in der die Winkelbeweglichkeit der Abtriebswellen im Differential-Gehäuse integriert ist (Schwenken in den beiden zusätzlichen Kegelrad-Paarungen an den Getriebeausgängen) und im gemeinsamen Punkt P_M erfolgt, wurde aber wegen der aufwändigen Herstellung und der ungenügenden Öl-Dichtheit des Differential-Gehäuses von der Zweigelenk-Pendelachse verdrängt (Abb.2). Letztere besitzt außerhalb des Differentialgetriebes zwei winkelbewegliche Kupplungen (meistens Kardangelenke). Die damit verbundene Pendel-Verkürzung verleiht der Achse den Nachteil des höher liegenden Wankzentrums P_M (Bedeutung: siehe unten).

3. Sturz und Spurweite  ↑ Anfang

Durch die Quasi-Trennung einer Starrachse in zwei in etwa mittig am Fahrzeugkörper pendelnd angelenkten Hälften wurden zwei voneinander unabhängige (Einzel-) Radaufhängungen gewonnen. Verloren ging aber der die Starrachse auszeichnende Vorteil des beim Einfedern nicht ändernden Radsturzes und der konstant bleibenden Spurweite. Beim Überfahren eines Buckels mit nur einem Rad ändert sich der Radsturz nur nicht an der anderen Seite. Das dortige Rad radiert aber in Querrichtung, denn der kinematisch erzwungenen Spuränderung widersetzen sich beide Räder mit je einer Reibkraft gegen den Boden. Das Radieren (gleitende Reibung) der Räder wirkt sich besonders bei Kurvenfahrt negativ aus. Auch wenn die Verhältnisse während der Kurvenfahrt stationär (konstanter Antrieb, kein Bremsen, kein Ein-/Aus-Federn) sind, ist die Seitenführungskraft nicht optimal, wenn sich der Straßenkontakt infolge Sturzänderung von anfänglich auf ganzer Reifenbreite zur Kante hin verschiebt (Anmerkung 1).

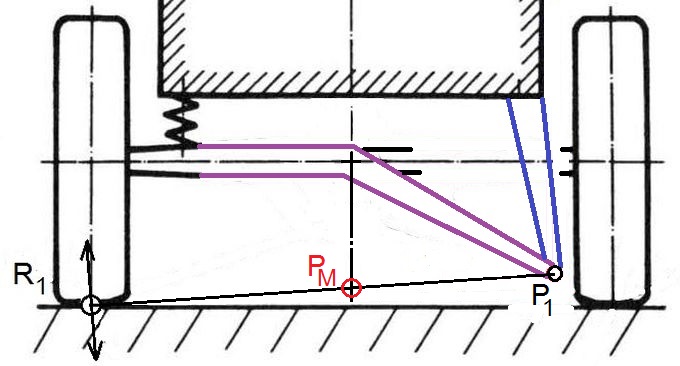Abb.4 idealisierte Pendelachse,
          schematisch; siehe Abb.5: [2]
          gezeichnet sind nur eine der beiden Halbachsen,
          nur eine Tragfeder und kein Antrieb

Damit sich Sturzwinkel und Spurweite der Räder beim Pendeln der Halbachsen möglichst wenig ändern, sollten die Pendellängen möglichst groß und die Pendel-Gelenke möglichst tief am Boden sein. Die Radaufstandspunkte bewegen sich dann auf relativ großen Kreisbögen und in Federungs-Mittellage annähernd (exakt bei Gelenken ganz am Boden) vertikal.

Als Pendellänge steht zwar die ganze Breite zwischen den Rädern zur Verfügung. Dafür müssten aber zwei außermittige Radantriebe benutzt werden, ein Aufwand, der meines Wissens nie betrieben wurde. Man blieb bei der Eingelenkachse, die in diesem Punkt der Zweigelenkachse überlegen ist.

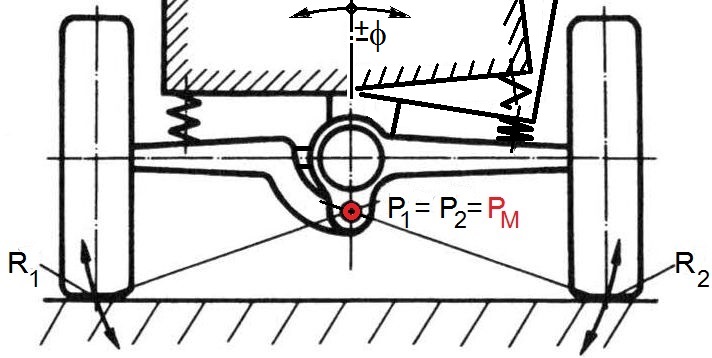Abb.5 Eingelenk-Pendelachse (schematisch; [2])
          am Mercedes Benz W 120 mit nach unten
          verschobeben Drehachsen (Rollzentrum P_M);
          angedeutet ist auch das Wanken ±Φ um P_M.

Mercedes-Benz benutzte seit Ende der 1950-er Jahre eine mässig verbesserte Eingelenk-Pendelachse mit Pendelgelenken am unteren Differentialgehäuserand (Abb.5), Pendelgelenke übertrieben tief gezeichnet). Wegen der inzwischen besser gewordenen Straßen konnte eine Verkleinerung der Bodenfreiheit gewagt werden.

4. Wanken um das Rollzentrum  ↑ Anfang

Die Tragfedern nahe jedes der vier Räder ermöglichen dem Fahzeugkörper außer seiner Ab- und Aufbewegung zum Mindern der von einer unebenen Fahrbahn verursachten Stöße auch Drehbewegungen um eine Quer- (Nicken) und um eine Längsachse (Rollen oder Wanken). Die letztere ist bedeutsam bei Kurvenfahrt, wenn sich der Fahrzeugkörper infolge der Fliehkräfte nach außen neigt (Abb.5): +Φ bei Fliekraft nach rechts). Für die Fahrzeuginsassen bedeutet das, dass sie sich gegen die Fliekraft stemmen müssen, und ihr Sitz sich dabei noch auf die falsche Seite neigt. Zur Komfort-Verbesserung wird deshalb der Wankwinkel mit Hilfe von Stabilisator-Federn verkleinert. Diese federn antiparrallel, so dass das im Normalbetrieb parallel erfolgende Ein-und Ausfedern der Basis-Federn von ihnen nicht beeinflusst wird.

Das Zufügen von Stabilisator-Federn und ähnliche Maßnahmen, beeinflussen aber auch die Fahreigenschaften während der Kurvenfahrt. Dabei ist das Besondere, dass sich nicht nur der Fahrbahn-Kontakt der beiden Räder der behandelten Achse, sondern auch der der beiden anderen Räder ändert. Allenfalls müssen an beiden Achsen Maßnahmen ergriffen werden, damit ein vorher "neutral" abgestimmte Fahrzeug nicht zu einem "übersteuernden" oder "untersteuernden" Fahrzeug wird. Zu dieser Thematik: siehe auch meinem Aufsatz
Stabilisator- und Ausgleichsfeder am Auto .

Im Folgenden beschreibe ich die Wirkung des bei Pendelachsen im Vergleich mit allen anderen Einzelradaufhängungen relativ hoch liegenden Rollzentrums.

5. Das bei Pendelachsen relativ hoch liegende Rollzentrum  ↑ Anfang

Das Rollzentrum ist im Allgemeinen und im Besonderen bei der Zweigelenk-Pendelachse (Abb.2) ein nur momentan fiktiver Punkt P_M, der bei Wankbeginn in der Mittelsenkrechten der Fahrzeugachse liegt. Nur bei der Eingelenk-Pendelachse ist er real und unveränderlich, nämlich der Mittelpunkt der Halbachsen-Pendellager (Abb.n 1, 3, 5).

Bei der Pendelachse (meistens hinten) gibt es wegen des deutlich höherem Rollzentrums (insbesondere bei der Zweigelenk-Achse) als an der anderen Achse (meistens vorn) eine schlechtere Ausgangslage für die Auslegung auf ausgewogene Kurvenstabilität mit Hilfe der Federn. Das Rollzentrum ist näher beim Schwerpunkt des Fahrzeugaufbaus, wodurch der Hebelarm für das über die Federn zum Boden "laufende" Wankmoment klein, der Hebelarm für das die Federn nicht "berührende" Kipp-Restmoment (Anmerkung 2) aber groß ist. Die Radlastdifferenz ist hinten relativ groß und wird überwiegend vom Kipp-Restmoment bestimmt. Sie ist i.d.R. zu groß (erhebliche Übersteuerungstendenz) und durch Variation der Federn wenig beeinflussbar. Neben der mangelnden Spur- und Sturzkonstanz ist hiermit ein weiterer prinzipieller Nachteil der Pendelachse genannt. Mit Hilfe der formelmässigen Darstellung und der Gegenüberstellung einiger berechneter Werte sei dieser Sachverhalt näher beleuchtet. Vorher werden die für die Rechnungen verwendeten Formeln in Abb.6 mit Hilfe der Abb.7 erklärt.

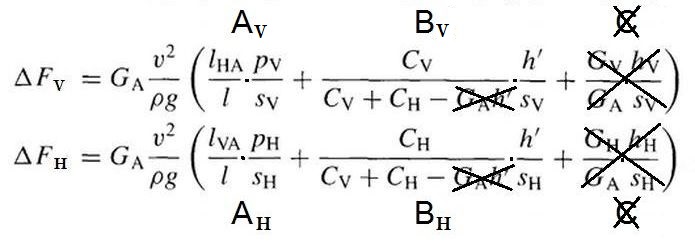Abb.6 Raflastdifferenz ΔF; [4]
          Indices: _V - vorne; _H - hinten
          G_A· v² / (ρ·g) = Fliehkraft FK
          l : Achsabstand
          l_A : Abst. Schwerp. - Achse
          s : Spurweite
          p : Höhe des Rollzentrums
          C : Federrate (Drehfeder um P_M)
          h' = h - p

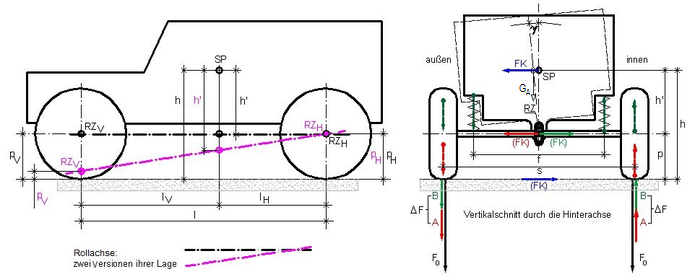Abb.7 Skizze: weitere Formelzeichen für Gleichungen in Abb.6:
          SP = Schwerpunkt des Fahrzeugkörpers (Höhe = h)     p_V---p_H = Rollachse     FK = Fliekraft     ΔF = Radlastdiff.

In Abb.7, rechts ist ein Kraft- und Momentengleichgewicht in der vertikalen Ebene durch die Hinterachse dargestellt. Es beruht auf der vorläufigen Annahme, dass sich der Schwerpunkt SF des Fahrzeugaufbaus in dieser Ebene befindet und die Fliehkraft FK folglich nur zu einer Radlastdifferenz ΔF_hinten führt. Als vorläufiges Modell kann man sich auch einen Einachsanhänger mit Schwerpunkt über der Achse vostellen.

Die horizontale Reaktion auf die Fliehkraft FK ist die Seitenführungskraft (FK) (am Boden mittig gezeichnet, in Realität zu etwa gleichen Teilen an beiden Rädern entstehend).
Das Gesamt-Kippmoment FK · h wird in zwei Teile zerlegt, die auf unterschiedliche Weise an der Entstehung der Radlastdifferenz vorn und hinten beteiligt sind.
Zu diesem Zweck werden zwei sich gegenseitig aufhebende, weil zueinander entgegengesetzt gerichtete Kräfte (FK) und (FK) am Rollzentrum RZ angebracht.
Die beiden Teilmomente, d.h. die Kräftepaar-Drehmomente aus (FK) / (FK) (Parallel-Abstand = p) bzw. aus (FK) / FK (Parallel-Abstand = h') ersetzen das Gesamt-Kippmoment.
Die Reaktionsmomente auf diese beiden Kräftepaar-Drehmomente (Teilmomente) sind die Kräftepaar-Drehmomente aus A bzw. aus B (Parallel-Abstand je = s). Die Summe A+B an jedem Radaufstandspunkt ist die Änderung der Radlast (an der Kurvenaußenseite vergrößernd, an der -innnenseite verkleinernd). Die zwei Kräfte A+B werden Radlastdifferenz genannt. Sie machen aus den beiden gleichen stationären Radlasten F₀ (aus dem Fahrzeuggewicht stammend) zwei ungleiche Radlasten.

Mit Hilfe von Abb.7, links soll die Abhängigkeit der Radlastdifferenz-Verteilung vorn/hinten von der Neigung der Rollachse erklärt werden. Das obige Modell Einachsfahrzeug ist jetzt aufgegeben. Die Fliehkraft FK wirkt anteilig auf beide Achsen, an dren Rädern je eine Radlastdifferenz entsteht.
Zwischen der vorderen und der hinteren Radlastdifferenz besteht kein einfacher proportionaler Zusammenhang gemäß unterschiedlichem Abstand der Achsen vom Schwerpunkt SP. Das gilt nur für den Radlastdifferenzteil A. Der Radlastdifferenzteil B wird aber der jeweiligen Wank-Federsteifigkeit der Achse entsprechend zugeteilt (Anmerkung 3)
Wird die horizontale Rollachse parallel verschoben, so bleiben die Radlastdifferenzen unverändert (Anteile A kleiner, Anteile B entsprechend größer). Das ist anders, wenn die Rollachse geneigt wird. Die magenta gezeichnete Rollachse ist vorne tief (Normalfall, wenn keine Starrachse: sehr nahe am Boden, auch beim VW-Käfer). Der Anteil A geht vorne gegen Null, während er hinten hoch bleibt. Die Anteile B werden zwar kleiner (in gleichem Maße vorn und hinten), aber unterm Strich ist die Radlastdifferenz hinten wesentlich größer (was den VW-Käfer so besonders übersteuernd machte). Die Ergebnisse der folgenden Rechnungen unterstützen das Gesagte in Zahlen (quantitativ).

Vorgaben für folgende Rechnungen:
 (l_VA/l=)  l_V/l = 0,55;   (l_HA/l=)  l_H/l = 0,45;   C_V = C_H;   s_V = s_H = 120cm;   h = 60cm;   Anmerkung 4

In der verwendeten Formel für die Radlastdifferenz ΔF (Abb.6) ist gegenüber der Originalformel [4] im Klammerteil B ein kleiner vernachlässigbarer Anteil gestrichen. Gestrichen ist auch der Anteil C, der die um eine Größenordnung kleinere Wirkung der Fliehkraft auf die Achsmassen (Radaufhängungen und Räder) berücksichtigt.

Der dimmensionslose Ausdruck A ist dem Einfluss des Rest-Kippmoments, B dem des Wankmoments proportional (Anmerkung 5).

1.   p_v/p_h = 35cm/35cm;     A_v/B_v = 0,131/0,104;   A_v+B_v = 0,235;     A_h/B_h = 0,160/0,104;   A_h+B_h = 0,265
2.   p_v/p_h =   5cm/35cm;     A_v/B_v = 0,019/0,160;   A_v+B_v = 0,179;     A_h/B_h = 0,160/0,160;   A_h+B_h = 0,321
3.   p_v/p_h =   0cm/40cm;     A_v/B_v = 0,000/0,158;   A_v+B_v = 0,158;     A_h/B_h = 0,183/0,158;   A_h+B_h = 0,342
3a. p_v/p_h =   0cm/40cm;     A_v/B_v = 0,000/0,238;   A_v+B_v = 0,238;     A_h/B_h = 0,183/0,079;   A_h+B_h = 0,263
4.   p_v/p_h =   5cm/10cm;     A_v/B_v = 0,019/0,218;   A_v+B_v = 0,236;     A_h/B_h = 0,046/0,218;   A_h+B_h = 0,264
4a. p_v/p_h =   0cm/10cm;     A_v/B_v = 0,000/0,227;   A_v+B_v = 0,227;     A_h/B_h = 0,046/0,227;   A_h+B_h = 0,273
(Anmerkung 6)

Fall 1: für die in Abb.7 schwarz gezeichnete Rollachse.
Die beiden Rollzentren sind gleich und relativ besonders hoch (Starrachse vorn und hinten).
Die Wankneigung ist klein (ΣA > ΣB).
Die Radlastdifferenz (A+B) ist hinten nur wenig größer als vorn. Mit einem mässig starken Satabilisator vorn wird das Fahrverhalten in Kurven ausgeglichen.

Fall 2: für die in Abb.7 magenta gezeichnete Rollachse.
Das vordere Rollzentrum liegt relativ tief (moderne Einzelradaufhängung), die Rollachse steigt erheblich nach hinten an (Anmerkung) 6)
Die Wankneigung ist größer (ΣB > ΣA).
Die Radlastdifferenz (A+B) ist hinten mehr fast doppelt so groß wie vorn. Das Fahrzeug neigt stark zum Übersteuern.

Fall 3: für Pendelachse hinten.
Das vordere Rollzentrum liegt in Bodenhöhe (z.B. VW-Käfer mit Kurbellenker-Radaufhängung), das hintere besonders hoch (Zweigelenk-Pendelachse z.B. beim VW-Käfer). Die Rollachse ist besonders steil nach hinten ansteigend.
Die Wankneigung ist ähnlich wie im Fall 2.
Die Radlastdifferenz (A+B) ist hinten mehr als doppelt so groß wie vorn. Das Fahrzeug neigt besonders stark zum Übersteuern.

Fall 3a: für Pendelachse hinten mit Ausgleichsfeder (s. unten und Anmerkung 7).
Im Vergleich zum Fall 3 ist die Wank-Federrate hinten auf ein Drittel, d.h. ziemlich drastisch verkleinert.
Dadurch werden die Radlastdifferenzen (A+B) hinten und vorn annähernd gleich groß. Das Fahrzeug neigt nur noch wenig zum Übersteuern. Die Wankneigung bleibt gleich.

Fall 4: für moderne Fahrzeuge (weder Starr- noch Pendelachse !! ).
Die Rollachse liegt tief und steigt nur geringfügig nach hinten an. Die Radlastdifferenzen (A+B) sind ohne besondere Maßnahmen etwa gleich groß: hinten etwas größer als vorne, was durch den als Maßnahme gegen das Wanken vorne meistens vorhandenen Stabilisator ausgeglichen wird. Die Wankneigung ist sehr groß (ΣB > 6 · ΣA); sie wird verringert, indem nicht nur vorne, sondern auch hinten ein Stabilisator eingebaut wird (vorne einer mit größerer Federrate als hinten). Da ΣB > 6 ΣA, ist der Spielraum für den Ausgleich der Radlastdifferenz vorn/hinten mittels Stabilisatoren konfortabel groß.

Fall 4a: für moderne Fahrzeuge, Variante.
Dieser Fall dient nur für den folgenden Vergleich mit Fall 3. Das vordere Rollzentrum liegt wie im Fall 3 am Boden.

Das bei Pendelachsen relativ hoch liegende Rollzentrum

Bezogen wird auf tief liegendes Rollzentrum, der Fall 3 wird auf den Fall 4a bezogen.
Das relativ hoch liegende Rollzentrum bewirkt, dass das Rest-Kippmoment hinten größer (A_H: 0,046 → 0,183; Differenz 0,137), das hinten abzustützende Wankmoment aber nur z.T. kleiner ist. Das Gesamt-Wankmoment ist kleiner, weil die Rollachse dem Schwerpunkt SP näher ist, bleibt aber unabhängig von der Lage der Rollachse auf die beiden Achsen nach dem Verhältnis der Wank-Federraten (das sich bei vorliegender Betrachtung nicht ändert) verteilt (B_H: 0,227 → 0,158; Differenz 0,069). Die hintere Radlastdifferenz ist im Fall 3 (Pendelachse) um den Wert 0,68 höher als im Fall 4a (vorne um den gleichen Wert niedriger). Zusammenfassung: Das bei Pendelachsen relativ hoch liegende Rollzentrum führt zu einer wesentlich höheren Radlastdifferenz als an der anderen Achse (mit niedrigen Rollzentrum). Besonders nachteilig ist, dass diese Differenz vorwiegend aus einem hohen Rest-Kippmoment stammt und schlecht über das kleine Wankmoment (bzw. über die mit den Tragfedern erzeugten Wanksteifigkeit) beeinflussbar ist.

Beispiele für die Anwendung von Ausgleichsfedern
Das Rezept zur Reduktion der Übersteuerungstendenz einer (hinteren) Pendelachse ist der Umbau der Federung: Die Tragfedern (Basisfedern) werden weicher gemacht, und eine Ausgleichsfeder wird hinzugefügt. Siehe auch meinen Aufsatz Stabilisator- und Ausgleichsfeder. Die dort in Abb.4 gezeigte Konstruktion mit Schrauben-Ausgleichsfeder-wurde von Mercedes-Benz im W120 und in Folgemodellen angewendet (Abb.8: W108). Beim VW-Käfer kam eine sogenannte Z-Feder zum Einsatz (Abb.9).

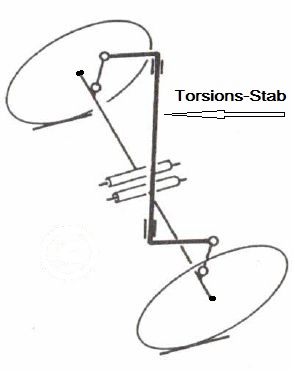Abb.8  Pendelachse Mercedes-Benz W108 mit Schrauben-Ausgleichsfeder; [3]
Abb.9  Z-Stab-Ausgleichsfeder (Torsions-Stab, [5]); z.B. am VW-Käfer (dort unter der Achse eingebaut)

6. Anmerkungen  ↑ Anfang

Anmerkung 1: Die Schmalreifen in Abb. 3 wurde längst wegen besserer Bodenhaftung infolge größerer Aufstandsfläche von Breitreifen abgelöst.

Anmerkung 2: Das Gesamt-Kippmoment ist quasi ein "potentielles" Kippmoment, denn üblicherweise wird derjenige Drehmoment-Wert als Kippmoment bezeichnet, bei dem das Kippen des Fahrzeugs tatsächlich eintritt.

Anmerkung 3:
Die Buchstaben A und B entsprechen in den Abbn. 6 u. 7 einander, obwohl sie verschiedene Dimensionen haben (Abb.6: dimensionslose Summanden in den Gleichungen; Abb.7: Dimension Kraft).

Anmerkung 4: Die Vorgaben sind etwas idealisiert, um die Berechnung der prinzipiellen Zusammenhänge zu erleichtren. In Wirklichkeit, insbesondere bei hinteren Pendelachsen, liegt der Schwerpunkt oft noch weiter hinter der Mitte, und die hintere Wank-Federrate ist i.d.R. größer als die vordere.

Anmerkung 5: Die dimensionslosen Ausdrücke A und B korrespondieren in Abb. 7 mit den Kräftepaaren B und B, die multpliziert mit ihrem jeweiligen gegenseitigen Abstand p bzw. h' die Reaktion auf das Rest-Kippmoment bzw. das Wankmoment sind.

Anmerkung 6: Die Absolutwerte der Wank-Federraten und des Wankausschlags spielen bei der Rechnung keine Rolle.

Anmerkung 7: Durch Verwenden einer Ausgleichs-Feder (siehe auch meinen Aufsatz Stabilisator- und Ausgleichsfeder) wird der Wankausschlag durch die Verkleinerung der Wank-Federrate vergrößert. Mit Hilfe einer Stabilisator-Feder wird er verkleinert. Das Wanken aus Komfortgründen zu mildern lässt sich also nur mittels einer Stabilisator-Feder erreichen (wobei immer darauf zu achten ist, dass dadurch auch die Fahreigenschaften in der Kurve beeinflusst werden ! ).
Bei der Verkleinerung der Federrate durch Benutzen einer Ausgleichsfeder kann es ratsam sein, die Rechnung unter Einbezug der oben (Abb.6) vernachlässigten "Gewichts-Rate" G_A·h' vorzunehmen.

7. Literatur  ↑ Anfang

[1] Erich Henker: Fahrwerktechnik, Vieweg, 1993, Seite 109, Tafeln 2.1, d).
[2] Reimpel/Betzler: Fahrwerktechnik: Grundlagen, Vogel Fachbuch, 2005, Seite 182, Bild 3.35.
[3] www.blankenhagen-service.de
[4] Mitschke/Wallentowitz: Dynamik der Kraftfahrzeuge, Springer, 2014, Seite 824.
[5] Wolfgang Matschinsky: Radführungen der Straßenfahrzeuge, Springer, 2007, Seite 88, Bild 5.16, c.

 ↑↑ Anfang

<< andere Fahrzeugtechnik-Beiträge
<< Home