<< Home
<< andere Fahrzeugtechnik-Beiträge
↓↓ Ende
Mausefallenauto
Seit ein paar Jahren werden im Schulunterricht kleine mit der Feder einer Mausefalle angetriebene Fahrzeuge gebaut und damit Wettbewerbe (meistens Weitfahr-, seltener Schnellfahrwettbewerbe) veranstaltet. Das hat außer die Eltern zur Mithilfe auch andere Erwachsene angeregt, selbst so eine Konstruktion zu erstellen. Ich wurde damit bekannt und als Ingenieur darauf neugierig, als uns ein Bub in der Verwandtschaft Bilder von seinem einschlägigen Eigenbau schickte. Wegen der Coronakrise ist es bisher zu keinem Kräftevergleich gekommen. Vorläufig kann ich nur von meinen in Klausur stattgefundenen Trockenübungen berichten.
Im Web berichtet über solche Fahzeuge umfangreich ein Modellbauer, der sich des Problems durch Anregung seines Sohns annahm und diesen unterstützte, Wettbewerbssieger in dessen Schule zu werden:
Dirk Raschke -Mausefallenautos. Ich werde mich im Folgenden mehrmals auf seine Berichte beziehen.
Inhalt
1. Der Energievorrat in einer gespannten Mausefalle
2. Mein Mausefallenauto # 1
3. kleine Änderungen am Auto # 1
3.1 kleinerer Wickeldurchmesser des Fadens
3.2 Einbau von Kugellagern in die Räder
4. Pläne für ein Auto # 2
4.1 größere Räder
4.2 Mausefalle mit besserer Drehfeder
4.3 Fadenumlenkung über einen erhöhten Punkt
5. Voruntersuchungen für den Bau eines Autos # 2
5.1 Federkräfte
5.2 Federsteifigkeit
5.3 Die Streckgrenze beim Biegen des Federstahldrahtes
5.4 Die Übersetzungsverhältnisse im Hebel-Faden-Mechanismus
6. Mein Mausefallenauto # 2
6.1 Planung
6.2 Aufrüstung
6.3 Fahrversuche und -ergebnisse
7 Schlussbemerkungen
8. Anmerkungen
9. Nachtrag
1. Der Energievorrat in einer gespannten Mausefalle
Welche Einschränkungen bezüglich der zu verwendeten Mausefalle gelten, weiß ich nicht genau, da ich noch keine Wettbewerbsausschreibung gesehen habe (Anmerkung 1).Es scheint aber so zu sein, dass die klassische, auf einem Holzbrettchen von 10cm mal 5cm angebrachte Schlagfalle (die Maus wird beim Fang erschlagen) zu wählen ist. Manche Schulen bemühen sich um gleiche Wettbewerbschancen, indem sie die Fallen en gros einkaufen und jedem Schüler eine davon abgeben.
Mehrere von mir erworbene Fallen haben übereinstimmend folgende technische Daten (Anmerkung 2):
• Bügel aus Draht mit Ø = 1,8 mm, Breite ≈ 41 mm, Höhe = 42 mm,
• Drehfeder (Schenkelfeder) aus Draht mit Ø =1,3 mm, 24 Windungen mit mittlerem Ø ≈ 5,2 mm,
• Drehmoment der vorgespannten Feder Mvor ≈ 0,042 Nm (1N·42mm, Speckseiten-Endlage, "Vorspannung"),
• Drehmoment der max. gespannten Feder Mmax ≈ 0,252 Nm (6N·42mm, über 180°-Winkel voll aufgezogen),
• Federsteifigkeit c = 0,21Nm / 180° (linear angenommen, berechnet aus den beiden gemessenen Drehmomenten).
Im Folgenden wird die Falle mit diesen Eigenschaften als "Standardmausefalle (6|1)" bezeichnet
 Abb.1 Europäische Standard-Mausefalle
Abb.1 Europäische Standard-Mausefalle
 << Abb.2 US-amerikanische Fallen
<< Abb.2 US-amerikanische Fallen
oben: Rattenfalle
unten: Mausefalle
Als beim Auslösen der Falle herunter schwenkende Speckunterlage (oder Käse-, s. Abb.1) dient in Mitteleuropa ein etwa 20mm breites, aus dem Brettchen frei gesägtes Stück. In anderen Ländern (USA u.a.) wird dafür ein an dieser Stelle aufgesetzer blecherner Hebel (Abb.2) benutzt. Da ein solches Schwenkstück und der von ihm frei gegebene Drahtstab, der den Schlagbügel gespannt hält, am Mausefallenauto nicht gebraucht werden, dürfen sie wohl entfernt werden. Der Schlagbügel darf direkt oder indirekt (an ihm angebrachten Faden) von Hand gehalten und beim Start losgelassen werden.
Rattenfallen sind deutlich größer. Zudem varriieren ihre Energie-speichernden Federn deutlich. Die Falle in Abb.2 enthält in etwa zwei gleiche Federn wie eine Mausefalle. Es gibt aber auch Rattenfallen mit nur einer und relativ kurzen Feder, also weniger speicherbarer Energie.
2. Mein Mausefallenauto # 1
Mein erstes Weitfahr-Mausefallenauto baute ich mit einer der o.g. Fallen. Es diente mir als Prototyp, bei dem ich einige Grundsätze wie Leichtigkeit und Reibungsarmut beachtete, es aber noch nicht quantitativ ausgefeilt konstruierte.
Es bekam drei CD-Scheiben als Räder, von denen die beiden hinteren angetrieben sind. Verbunden sind sie mit einer gekürzten Fahrradspeiche (Ø = 2 mm) als Achse, die lediglich in zwei Ringkopfschrauben (Ring-Ø = 3 mm, innen) drehbar gelagert ist. Das Vorderrad dreht mit seinen beiden Achsstummeln (Ø = 2 mm) in zwei kurzen Messinghülsen (Ø = 3 mm, innen). Die beiden Längsholme des Fahrgestells bestehen aus Balsa-Holz, die übrigen kürzeren Teile aus dem dreimal schwereren Fichtenholz. Den Fallenhebel verlängerte ich auf 44 cm (ein mehr oder weniger zufälliger Wert) mit einem Stab aus Fichtenholz (Hochkant-Profil 11mm x 3,5mm).
Für das Aufwickeln des Fadens wurde eine Garnrolle (Ø = 3 mm, außen) auf die Achse gepresst. Der rückdrehende Hebel kann
0,88 m Faden von der Spule abziehen, womit sich theoretisch 33 m weit fahren lässt:
Fadenlänge x Disc-Ø/(Spulen-Ø+Faden-Ø) = 0,88 x 120 / (3+0,2).
Diese Distanz hat mein Auto #1 auf dem Parkett-Boden unseres Wohnzimmers sicher erreicht (mehrmaliges Wenden nach jeweils knapp 5 Metern) Teilstrecke).
 Abb.3 Mausefallenauto # 1 Draufsicht startet nach Wegnahme der Wäscheklammer
Abb.3 Mausefallenauto # 1 Draufsicht startet nach Wegnahme der Wäscheklammer
 Abb.4 Mausefallenauto # 1
Abb.4 Mausefallenauto # 1
links: Vorderrad
rechts: Nabe des linken Hinterrades und Hinterachse mit Fadenspule, gelagert in Ringkopfschrauben
 << Abb.5 Mausefallenauto # 1;
<< Abb.5 Mausefallenauto # 1;
Mausefalle mit an Bügel montiertem Stab
oben: seitliche Ansicht
unten: Draufsicht
3. kleine Änderungen am Auto # 1
3.1 kleinerer Wickeldurchmesser
des Fadens
Diese Änderung ließ sich leicht verwirklichen. Ich entfernte die Garnspule und wickelte den Faden direkt auf die 2 mm dicke Achse auf. Das Auto fuhr jetzt weiter, erreichte die dadurch auf 48 m vergrößerte (Vergrößerungsfaktor = 3,2/2,2) Distanz aber nicht sicher immer.
3.2 Einbau von Kugellagern in die Räder
Die inzwischen beschafften Kugellager haben die Durchmesser 3 mm/innen und 10 mm/außen. Hinten wurden ihre Außenringe in eine zylindrische Vertiefung (etwa 1/3 eines ganzen Zylinders) in der Stirnseite der Gestellholme eingelegt. Gehalten werden sie von je einem flachprofiligen Gummiring, so dass die Hinterachse leicht demontierbar ist. Die 48 m lange gezogene Fahrt gelang sicher. Mit ein paar Metern Nachrollen des Autos wurde die 50m-Marke überboten.4. Pläne für ein Auto # 2
4.1 größere Räder
Reibung besteht nicht nur in den Lagerstellen sondern auch beim Rollen der Räder auf der Fahrbahn. Bei größeren Rädern ist die Rollreibung kleiner. Beim Wechsel auf größere Räder ist zwar mehr Masse zu bewegen, was die Reibungsverluste wieder steigert. Ich erwarte aber, dass die Reibungsverluste unter dem Strich kleiner sein werden. Nebenvorteil ist die größere Wegübersetzung vom Fadenwickel auf der Achse zum Radaufstandspunkt. Die bereits dünne Achse muss nicht weiter geschwächt werden, wenn der Fahrweg vergrößert werden soll.Möglicherweise sind kleinere Kugellager reibungsärmer, da der Wälzkreis der Kugeln kleiner ist (Hebelarm des vom Wälzen der Kugeln verursachten Bremsmomentes ist kleiner).
4.2 Mausefalle mit besserer Drehfeder
Die auf dem Markt befindliche Falle mit stärkster Feder ist zu finden.4.3 Fadenumlenkung über einen erhöhten Punkt
Die Mausefallenautos mit Hebel und Faden werden ab etwa 135° bis 150° des Hebel-Rückdrehens nicht mehr angetrieben. Der Hebel schlägt plötzlich auf seinen Anschlag bei 180°herunter (siehe z.B. hier). Ein noch vorhandener Teil der in der Feder gespeicherten Energie verpufft auf diese Weise in einem Stoß zwischen Hebel und Anschlag (Anmerkung 3). Für den Vortrieb des Autos geht er verloren. Ursache ist die gegen Null klein werdende Übersetzung auf den Fadenweg. Die dazu inverse Kraftübersetzung wird hingegen unendlich groß. Der Faden dehnt sich und die Antriebsachse verbiegt sich, so dass der Hebel durchschlägt.Um diesen störenden Effekt zu vermeiden, müsste die Übertragung zwischen Fallenhebel und Faden geändert werden. Anstatt einer entsprechenden aufwändigen Maßnahme (z.B eine Kurvenscheibe) lässt sich die Störung bereits durch einmaliges Umleiten des Fadenlaufs im letzten Teil des Hebelrückdrehens über einen erhöhten Punkt mindern. Auf diese Weise nähert sich am Schluß der Winkel zwischen Faden und Hebel nicht Null, und eine kleine Restmenge der in der Feder gespeicherte Energie wird genutzt. Die Lage dieses Punktes relativ zum Hebel-Faden-Radachsen-Mechanismus hängt auch von der Kennlinie der Mausefallen-Feder (Federrate und Vorspannung) ab.
Eine Kurvenscheibe stellt einen Hebel mit stetig kleiner werdender Länge dar. Als Alternative dazu würde sich anbieten, den Wickeldurchmesser des Fadens an der Antriebsachse dort zu vergrößern, wo die Fadenkraft verkleinert ist. Dieses Prinzip wird in einem Federhaus mit Schnecke in mechanischen Uhren angewendet.
5. Voruntersuchungen für den Bau eines Autos # 2
5.1 Federkräfte
Zur Teilnahme an einem Wettbewerb wird die zu verwendende Mausefalle vorgeschrieben. Oft wird sogar ein Exemplar davon an den Teilnehmer abgegeben. Die Kenngrößen der Mausefallenfeder stehen somit nicht zur Disposition. Der Teilnehmer hat sein Fahrzeug damit auszurüsten und deren real existierenden Kenngrößen in seine Konstruktion aufzunehmen. Äußerlich scheinen alle, oft sogar von verschieden Herstellern stammende Fallen gleich zu sein. Dennoch sind die am Mausefallenhebel gemessenen Spannkräfte nicht immer gleich groß. In diesem Falle darf sich der Konstrukteur eines Mausefallenautos fragen, warum er es mit einer Mausefalle mit etwas anderen Eigenschaften zu tun hat als sein Kollege. Das nützt ihm zwar in seiner momentanen Situation gar nichts, bringt ihn aber etwas Grundsätzlichem in der Technischen Mechanik näher. Über das Grundsätzliche beim Biegen eines Drahtes, wie er in aufgewickelter Form als Schenkelfeder in einer Mausefalle eingebaut ist, sei im Folgenden berichtet.
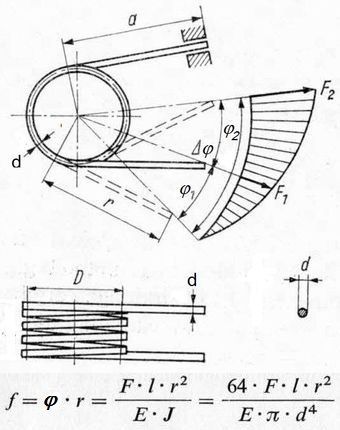 << Abb.6 Drehfeder (oder Schenkelfeder) Ausführung und
<< Abb.6 Drehfeder (oder Schenkelfeder) Ausführung und
Kennlinie (Graphik und Formel)
[Siegfried Hildebrand: Feinmech. Bauelemente,
Hanser, 1968, Seiten 308 und 310]
Einleitend erinnere ich an den dem Leser i.d.R. bekannten Biegegestab, einem geraden Stab mit der Länge l, der an einem Ende fest eingespannt ist und am anderen quer von einer Kraft F belastet wird. Sein freies Ende weicht über den Weg f in Richtung der wirkenden Kraft F aus:
f = F·l3 / (3·E·J) . (1)
Er tut das umso mehr, je größer die Kraft F ist. Seine Länge l geht überproportional mit der dritten Potenz ein.
Er weicht aber umso weniger aus, je größer der Widerstand E (Elastizitätsmodul) des Materials gegenüber elastischer Verformung ist. f ist ebenfalls um so kleiner, je dicker der Stab ist. Das wird mit dem sogenannten Flächenträgheitsmoment J, das die geometrische Eigenschaft Stabquerschnitt bzw. Querschnittsfläche berücksichtigt:
J = π·d4 / 64 (2)
Die Dicke ist im vorliegenden Fall der Durchmesser d des Federdrahts, der sogar in vierter Potenz in f eingeht. .
Eine Drehfeder ist ein in Schraubenlinie auf einen Zylinder gewickelter Biegestab. Im Unterschied zum geraden Stab ist das in ihm wirkende Biegemoment über fast seine gesamte Länge konstant. Nur in den zur gewickelten Länge relativ kurzen Schenkeln variiert es (von den Enden her linear bis zum konstanten Wert im Wickel ansteigend). Die in den Schenkeln aufgenommene und gespeicherte Verformungsarbeit kann gegenüber der im Wickel vernachlässigt werden. Die in Abb.6 unten stehende quantitative (Formel-) Darstellung des elastischen Verhaltens einer Feder ist prinzipiell vergleichbar mit der oben stehenden Formel (1) für den geraden Biegestab.
Aus Abb.6 wird der mittlere Formelteil als Formel (3) entnommen und der Formel (1) gegenübergestellt:
f = F·l·r2 / (E·J) , (3)
f = F·l3 / (3·E·J) . (1)
In Formel (1) geht l sowohl als Hebelarm des biegenden Momentes M = F·l als auch als Länge des gebogenen Stabes ein.
In Formel (3) sind der Hebelarm r und die Länge l des gewickelten Stabes, der gebogen wird, getrennt aufgenommen.
Mit dem Faktor 1/3 in Formel (1) wird berücksichtigt, dass das den Stab belastende Biegemoment nicht über dessen Länge konstant ist, sondern mit dem Wert Null am freien Ende beginnt und linear bis zum Endwert F·l ansteigt.
Beim geraden Biegestab interessiert für die Angabe der Verbiegung der Durchbiegung genannte Weg f. Bei der Schenkelfeder (Drehfeder) steht der Verdrehwinkel φ im Vordergrund. Mit φ = f / r entnimmt man Formel (3a) aus (3):
φ = F·l·r / (E·J) , (3a)
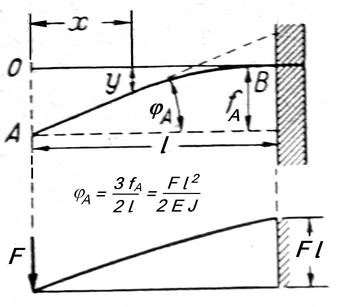 << Abb.7 gerader Biegestab ("Freiträger")
<< Abb.7 gerader Biegestab ("Freiträger")
Einzellast F am freien Ende A
[Hütte - des Ingenieurs Taschenbuch,
Ernst & Sohn, 1955, Seite 872]
Die von Bernoulli (1655 bis 1705) begründete Balkentheorie hat Navier (1785 bis 1836) in der folgenden kurzen Formel umfassend formuliert.:
Krümmung = Biegemoment / Biegesteifigkeit >>>>
χ = M / (E·J) (Anmerkung 4).
Aus der Krümmung χ folgt durch Integration über die Balkenlänge l die Verdrehung φ zwischen voneinander entfernten Balkenquerschnitten.
Aus der mit M = F·l geschriebenen Bernoulli-Navier-Formel folgt nach der Integration die Formel (3a), wie leicht nachvollzogen werden kann.
Die Formel (1a) für die Verdrehung φA am freien Ende des geraden Biegestabes wird in analoger Weise gefunden, nur ist das nicht so leicht nachvollziebar (Faktor 1/3 in (1), aber Faktor 1/2 in (1a); man beachte auch, dass der sich im Gebrauch einstellende Verdrehwinkel φ des Biegestabes eine Größenordnung kleiner als der der Drehfeder ist):
φA = F·l2 / (2·E·J), (1a), siehe Abb.7
(3a) und (1a) unterscheiden sich voneinander lediglich infolge der beim Integrieren befolgten, bereits o.g. unterschiedlichen Randbedingungen: über die Länge konstantes Biegemoment beim gewickelten Biegestab bzw. über die Länge nicht konstantes, also bezüglich seiner Wirkung weniger leicht überschaubares Biegemoment beim geraden Biegestab.
Es erweist sich somit, dass die Balkentheorie im Anwendungsbeispiel Drehfeder leichter zu verstehen ist als im Beispiel gerader Biegestab ("Freiträger", Anmerkung 5). Wer hätte gedacht, dass ausgerechnet die Beschäftigung mit einer Mausefalle zu dieser Erkenntnis führen kann !
5.2 Federsteifigkeit
Als Federsteifigkeit wird i.d.R. das Verhältnis c zwischen Federkraft und Federweg bezeichnet. Bei der Schenkelfeder wird das Verhältnis zwischen dem angebrachten Drehmoment und dem Verdrehwinkel φ angegeben, so dass die sowohl Kraft- als auch Weg-bestimmende Hebellänge (Schenkellänge) nicht in Escheinung tritt.
Dieses Verhältnis folgt aus dem linken Teil der Formel in Abb.6-unten (umgestellt und F·r zu M zusammen gefasst):
c = M / φ = E·J / l, (5).
Die Federn von sechs gekauften Mausefallen wurden mit ziemlich genau dem gleichen Drehmoment M = 5N ·42mm um π (= 180°) in die gespannte Lage verdreht: Die gemessene Federsteifigkeit ist c = 66,8 Nmm . Die Kennlinie solcher einfachen Federn ist meistens eine Gerade (c = konstant), was im vorliegenden Fall ohne zu zweifeln übernommen wurde.
Der theoretische Wert ist c = 75 Nmm .
Dafür wurden in die Formel (5) eingesetzt:
E = 2,1·105 N/mm2 (Elastizitätsmodul für Stahl),
J = 0,14 mm4 (errechnet mit d= 1,3mm in Formel (2)),
l = 24·5,2·π = 392 mm (24 Windungen mit mittlerem Wickeldurchmesser 5,2mm).
Die Abweichung vom tatsächlichen, dem gemessenen Wert kann der vernachlässigten Verdrehung (Biegung) der Schenkel geschuldet sein. Der verwendete Wert für den Elastizitätsmodul ist weniger in Frage zu stellen. I.d.R. unterschreiten gering legierte Federstähle den Stahl-Standard-Wert E = 2,1·105 N/mm2 nicht merklich. Nicht auszuschließen ist aber die Verkleinerung wegen eines geringes Untermaßes beim Drahtdurchmesser, der immerhin in vierter Potenz ins Ergebnis eingeht.
5.3 Die Streckgrenze beim Biegen des Federstahldrahtes
Eine Feder kann nur bis zu einem Grenzdrehmoment Mmax belastet werden. Bei dessen Überschreiten verdreht sie sich plastisch, d.h. bleibend. Die im Handel befindlichen Mausefallen sind leider schwach ausgelegt. Der verwendete Federdraht ist minderwertig, seine aushaltbare Biegespannung σB liegt am unteren Rand des üblichen Wertebereiches und wird bei etwa 7·42 Nmm belastendem Drehmoment überschritten (siehe folgenden Versuch mit den Fallen 5 und 6): Die dabei wirkende Biegespannung ist
σB = MB/ W = 7·42 Nmm / 0,251 mm3 >>> σBmax = 1'370 N/mm2 . (Biege-Widerstandsmoment W = J / (d/2))
Der im Geräte- und Maschinenbau üblich verwendete Federstahldraht ist bis mindestens σB = 2'000 N/mm2 elastisch.
Meine bisher 6 Mausefallen-Federn lassen sich nach wenigen Benutzungen mit nur M = 6·42 Nmm aufziehen. Umgekehrt: Mit nur diesem Drehmoment können sie das Mausefallenauto zu Beginn antreiben. Bei den beiden zuletzt angeschafften war ich euphorisch. Die im Laden trotz Verpackung messbare Vorspannung betrug M = 4·42 Nmm, was M = 9·42 Nmm nach dem 180°-Aufziehen versprach. Aber voll aufgezogen gaben beide sofort auf die bekannte mindere Güte nach. Die Mausefallen werden offensichtlich nach der Montage nicht probeweise aufgezogen. Beim Benutzen wird quasi die beim Wickeln des Drahtes stattgefundende plastische Verformung fortgesetzt: der mit dem Hebel verbundene Schenkel wird gegen den fixierten Schenkel um einige Dutzend Winkelgrade plastisch weiter vorwärts verdreht.
5.4 Die Übersetzungsverhältnisse im Hebel-Faden-Mechanismus
Die Fadenkraft wird in eine kleinere Kraft am Umfang der angetriebenen Räder übersetzt. Das Übersetzungsverhältnis zwischen diesen beiden Teilen ist konstant, wenn der Faden direkt auf der Antriebsachse und in nur einer Schicht aufgewickelt ist. Wenn nötig, lässt sich ein veränderliches Übersetzungsverhältnis realisieren, wenn der Faden auf einer nicht-zylindrischen Fadenrolle (Stichwort:Federhaus mit Schnecke; s.o.) aufgewickelt wird (oder bei Wechseln zwischen verschiedenen Wickelschichten).Anzustreben ist, dass die Faden- bzw. die Radumfangs-Kraft während der gesamten Fahrt des Autos konstant ist. Außer der selbstverständlichen Anfangsbeschleunigung beim Starten sollte danach kein Teil der Antriebsenergie für Geschwindigkeitsänderungen bzw. Beschleunigungen verbraucht werden. Solche Energie ist für die Fahrweite verloren.
Weil das von der aufgezogenen Mausefallenfeder abgegebene Drehmoment zwischen Anfang und Ende der Hebelrückdrehung linear abfällt, sollte sich die am Faden wirksame Hebellänge linear verkleinern. Länge und Drehstellung des wirksamen Hebels sind diejenigen, bei denen dieser fiktive Hebel und der Faden an seiner Spitze einen rechten Winkel) bilden. Auf diese Weise kann bei kleiner werdendem Drehmoment die Kraft am Faden konstant gehalten werden. Drehmoment ist Hebelarm mal Kraft, somit ist die Kraft konstant, wenn sich Drehmoment und wirksamer Hebelarm gleichermaßen verändern (im vorliegenden Falle verkleinern).
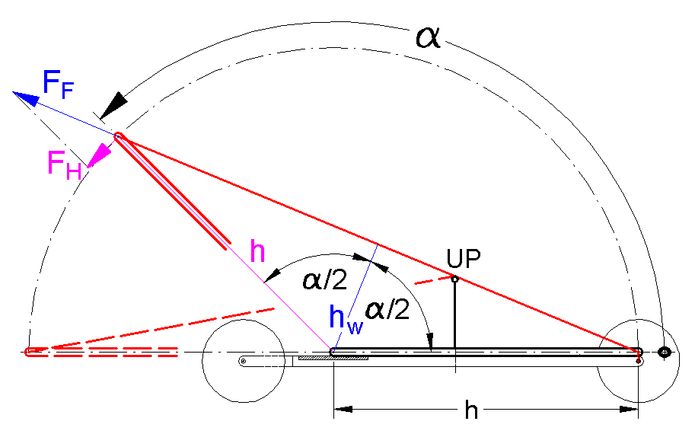 << Abb.8 Hebel-Faden-Mechanismus: Abhängigkeit
<< Abb.8 Hebel-Faden-Mechanismus: Abhängigkeit
der Faden- FF von der Hebelkraft FH
und dem Rücklaufwinkel α,
Fahrtrichtung nach links
Beim einfachen Hebel-Faden-Mechanismus ändert sich die wirksame Hebellänge hw (reale = h) in der tendenziell richtigen Weise. Sie wird kleiner, aber leider nicht linear mit der Hebeldrehung α:
hw / h = cos (α/2) (6) α = 0° >>> 180°
(Hebel aufgezogen >>> Hebel abgelaufen, s. Abb.8).
Die Kraft im Faden FF und die senkrecht am Hebelarmende wirkende Kraft FH stehen in umgekehrtem Verhältnis:
FF / FH = 1 / cos (α/2) (6a) ; umgestellt: FF = FH/ cos (α/2)
FF ergibt sich durch Division von FH durch cos(α/2) .
Abb.9 zeigt deutlich, dass die mit dem einfachen Hebel-Faden-Mechanismus erzeugte Fadenkraft (gezeichnet als grüne Linie) an Anfang kleiner und am Ende unendlich groß wird, also eine unvollkommene Näherung an einen konstanten Wert ist. Besonders ungenügend ist der bereits oben angesprochene Kraftverlauf gegen unendlich groß am Ende.
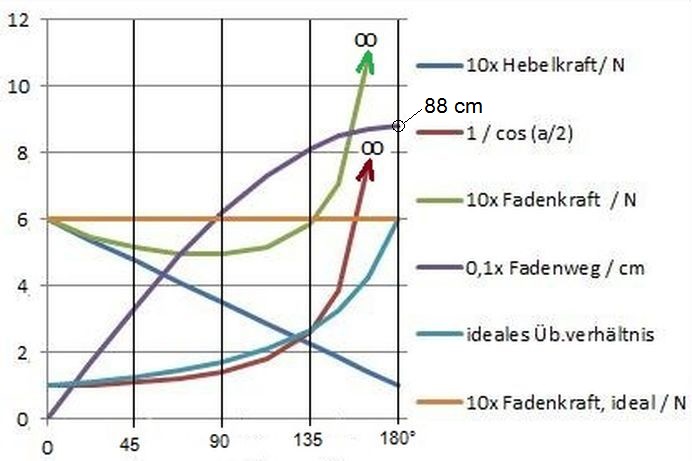 Abb.9 Kraft- und Übersetzungsverhältnisse im Hebel-Faden-Mechanismus
Abb.9 Kraft- und Übersetzungsverhältnisse im Hebel-Faden-Mechanismus
Drehmoment am Hebel: 6·42 Nmm (0°) | 1·42 Nmm (180°); Hebellänge: 440 mm
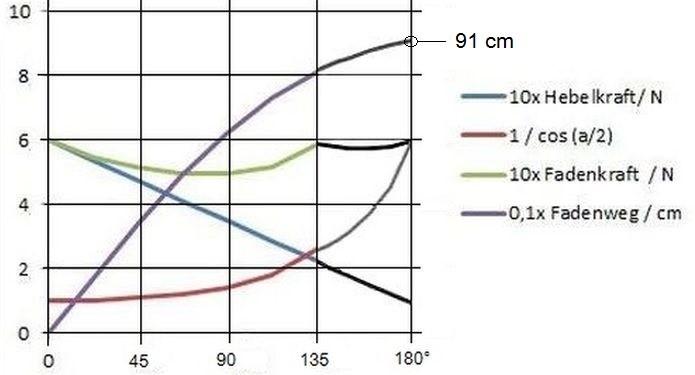 Abb.10 Kraft- und Weg-Übersetzung im Hebel-Faden-Mechanismus von Abb.9
Abb.10 Kraft- und Weg-Übersetzung im Hebel-Faden-Mechanismus von Abb.9
Unterschied: Fadenumlenkung ab 135° des Hebelrückdrehens
(in Abb.8 bereits eingezeichnet: UP)
Aus Abb.9 ist auch ersichtlich, dass die Fadenkraft in meinem Mausfallenaut #1 nach etwa α=135° des Hebel-Rücklaufs den Anfangs- (und Ideal-) Wert übersteigt. Da sie ab diesem Punkt nicht mehr ansteigen und in etwa konstant bleiben soll, muss der Fadenumlenkung (siehe Abschnitt 4.3) bei dieser Hebelstellung beginnen. Der Faden hat jetzt den Umlenkpunkt ereicht und gleitet bis zum Schluß der Hebelrückdrehung durch diesen. Probierentes Optimieren (s.Abb.10, letztes Diagrammviertel) mit dem Excel-Programm ergab als Punktkoordinate in Fahrrichtung eine Stelle kurz nach der Mitte zwischen Antriebsachse und Mausefalle (in Zahlen: 58% dieser Strecke ab Antriebsachse). Die Fahrstrecke erhöht sich theoretisch um knapp zwei Meter, was sich in einem Fahrversuch prinzipiell bestätigte (Umlenkung über einen Drahtbügel, der vorerst bei einem der mehrfachen Wendemanöver montiert wurde, nachdem dieser den Umlenkpunkt passiert hatte). Das hässliche Durchschlagen des Hebels ist beseitigt, die Streckenvergrößerung aber mit 91/88 eher mäßig ausgefallen.
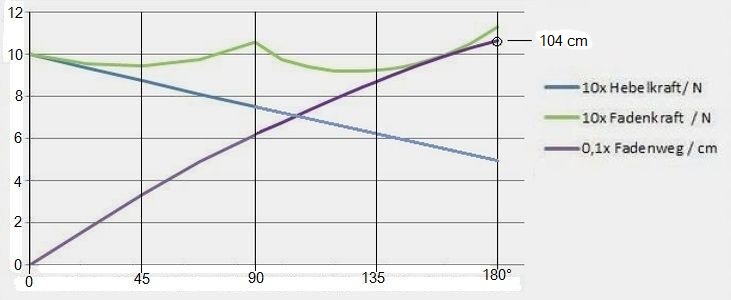
Abb.11 Kraft- und Weg-Übersetzung im Hebel-Faden-Mechanismus mit stärkerer Feder (5|10):
Drehmoment am Hebel: 10·42 Nmm (0°) | 5·42 Nmm (180°); Hebellänge: 440 mm
Fadenumlenkung bei 90° des Hebelrückdrehens
Die andere Quelle für ungleichmäigen Antrieb ist das Kraftminimum in der ersten Hälfte des Hebelrücklaufs. Bei Verwendung einer stärkeren Feder wird das streckenweise Durchhängen der Fadenkraftlinie wegen der relativ größeren Vorspannung zwar kleiner, kann durch eine Fadenumlenkung aber prinzipiell nicht vermieden werden. In Abb.11 ist zu sehen, dass die Fadenkraft bei stärkerer Feder (stärker vorgespannt, Anmerkung 6) zwar schon bei 90° Rückdrehen den Anfangswert überschritten hat, aber dass das anschließende Verkleinern und Glätten durch Fadenumlenken weniger gut gelingt. Es bietet sich an, den Faden in einem weiteren Punkt nochmals umzulenken (s. Abb.12).
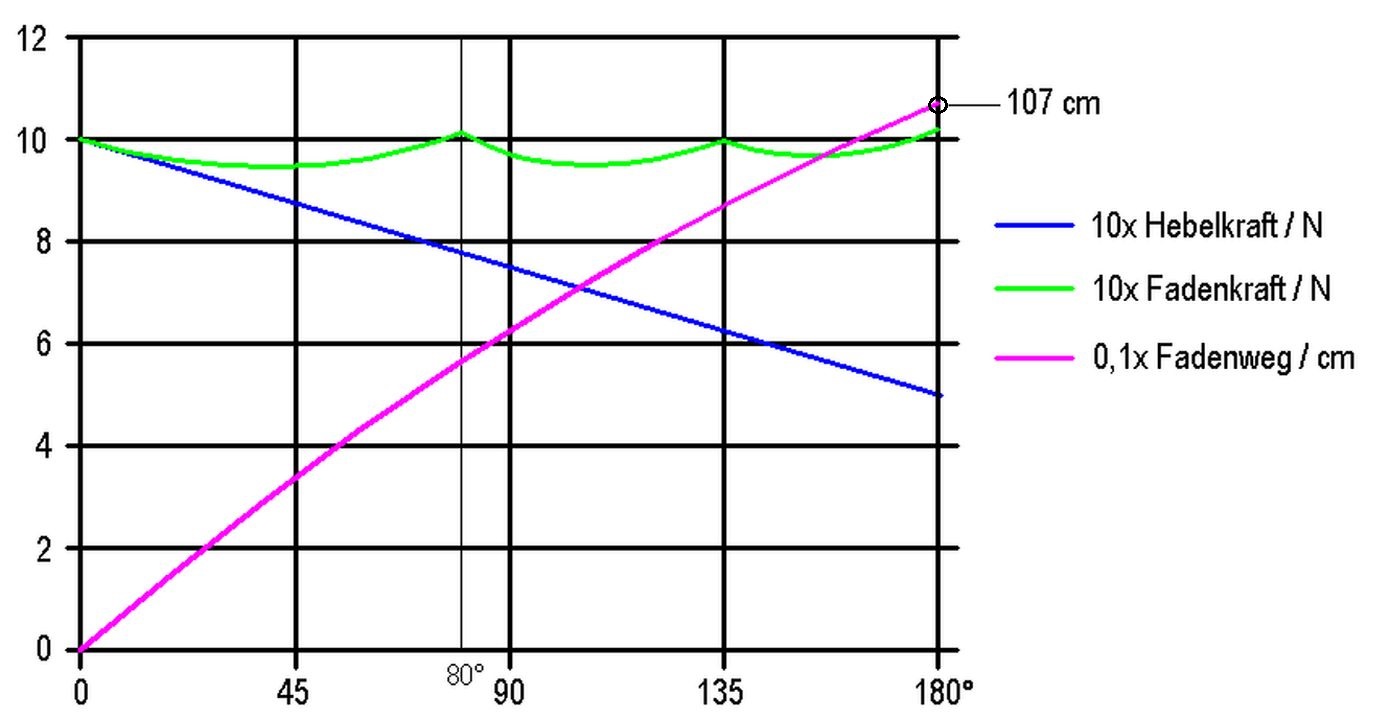
Abb.12 Kraft- und Weg-Übersetzung im Hebel-Faden-Mechanismus mit stärkerer Feder (5|10):
zwei Fadenumlenkungen: bei 80°und bei 135° des Hebelrückdrehens
Das Minimum der Fadenkraft ("Durchhängen") ist bei der Standardfeder (1|6) stärker ausgeprägt (83% des Anfangswertes) als bei der stärkeren Feder (5|10; 95%).
6. Mein Mausefallenauto # 2
Da meine durch Experimente gestützten Untersuchungen prinzipieller Natur sind, verzichte ich auf den Bau eines zweiten Autos. Sollte sich die Gelegenheit ergeben, an einem Wettbewerb teilzunehmen, genügt ohnehin ein Exemplar. Mein Mausefallenauto # 2 ist das getunte Mausefallenauto # 1.
6.1 Planung
Die geplanten größeren Räder beschaffte ich nicht. Ich begnüge mich mit den bereits mit Kugellagern ausgerüsten CD-Scheiben. Der o.g. Vermutung, dass größere Räder einen kleineren Rollwiderstand haben, der besonders auf nicht glatten Laufbahnen die Auslegung für eine etwas größere Reichweite ermöglicht, ging ich nicht nach.
Im Wesentlichen geht es mir darum, den Vorteil einer stärkeren Mausefallenfeder, die prinzipiell herstellbar ist, zu demmonstrieren. Für deren optimale Anwendung sehe ich wie o.g. (Ende des letzten Abschnitts) zwei Umlenkpunkte für den Fadenlauf vor. Die auch bereits angesprochene Variation des Wickeldurchmessers des Fadens auf der Antriebsachse werde ich nur insofern nutzen, dass zwei/drei zuerst ablaufende Wickel sich über darunterliegenden befinden. Der Hebelarm des abziehenden Fadens ist etwas größer, was die Beschleunigung aus dem anfänglichen Ruhezustand sicherer macht.
Genau genommen: Der Faden wird nicht mehr von der Achse der hinteren Räder abgezogen sondern von der angetriebenen Achse (Durchmesser ebenfalls 2 mm) eines vorgesehenen Zahrad-"Vorgelege"-Getriebes (Übersetzung ins Schnelle). Die bereits beschafften kleineren Kugellager (Innnendurchmesser 2 mm anstatt 3 mm) mit erwartetem kleineren Wälzwiderstand werden nur der Lagerung der Vorgelegeachse dienen.
Wie weit ein Mausefallenauto fahren kann, ist keine Zufallsgröße, sondern wird bei der Konstruktion festgelegt. In Realität wird diese "eingebaute" Entfernung erreicht oder das Auto bleibt an einer kleinen Unebenheit der Fahrbahn stehen. Der Konstrukteur hat lediglich eine kleinste von den Bahnverhältnissen (Unebenheiten) abhängigen erforderliche Antriebskraft an den Rädern anzunehmen (oder ermittelt sie durch Tests auf der vorgesehenen Bahn). Wenn es ihm gelingt, dass die vom an der Mausefalle angebrachten Hebel (Verlängerung deren Klapphebels) am Faden erzeugte Kraft beim Hebelrücklauf konstant ist, wird auch eine konstante Umfangskraft (Übersetzung ins Kleine) an den angetriebenen Rädern wirken, denn die weiter bestimmenden Abhängigkeiten (Fadenwickeldurchmesser, Übersetzung in einem allfälligen Rädergetriebe und der Raddurchmesser) sind konstante Größen. Die konstante Fadenkraft ergibt sich aus der Kennlinie der Mausefallenfeder und dem konstruierten Korrekturmmechanismus zwischen Hebel- und Fadenbewegung.
Die Fahrweite ist das Resultat aus der abgezogenen Fadenlänge und dem Weg-Übersetzungsverhältnis (ins Große) zwischen Fadenweg und Rollweg der angetriebenen Räder. Ohne Korrekturmaßnahmen ist der Fadenweg doppelt so groß wie die Hebellänge, mit Korrekturmaßnahmen erhöht sich dieser Wert.
Meine Vorgaben für das Auto #2 schloss ich aus den Fahrversuchen mit Auto #1 (das ich ohne Erfahrungen mehr oder weniger ins Blaue hinein gebaut und anschließend noch gering verbessert hatte). Es fuhr gerade sicher genug mit der Hebellänge 44 cm, dem Wickeldurchmesser des Fadens von 2,2 mm und dem Außendurchmesser der CD-Räder von 120 mm. Daraus ergab sich ein Fahrweg von 48 m (2·0,44 ·(120/2,2)). Auf den Bahndurchmesser von 88 cm des Schlaghebels einer durchscnittlichen Mausefalle normiert ist das eine Wegübersetzung ins Große von 1 : 54,5 (48m/88cm). Die Verwendung einer stärkeren Feder und das Vorhaben, noch sorgfältiger als bisher zu montieren (weitreichendes Vermeiden von Reibungen zwischen den bewegten Teilen) bestärkte mich darin, das etwa Dreifache (3-fach mit Vorgelegegetriebe, 42/44-fach mit kürzerem Hebel: 48m ·3·42/44 = 137,5 m) für die "einzubauende" Entfernung vorzugeben. Das genormte Wegeverhältnis ist mit 1 : 156 ebenfalls das knapp Dreifache desjenigen von Auto #1.
Die Radumfangskraft (verteilt auf zwei Räder) ist unter der Bedingung einer Korrektur im Hebel-Faden-Mechanismus 11·10-3 N (Auto #1: = 0,6N / 54,5) bzw. 6,4·10-3 N (Auto #2: =1N / 156).
6.2 Aufrüstung
Ich wollte nicht mehr länger darauf warten, bis ich doch einmal eine Mausfalle mit stärkerer Feder finden würde. Nachdem ich einen Lieferanten für Federstahldraht ausfindig gemacht und bei ihm gewöhnlichen Federstahldraht mit Durchmesser 1,3 mm kaufen konnte, wickelte ich damit selbst solch eine Schenkelfeder und tauschte die Orginalfeder der im Auto fest eingebauten Mausefalle gegen diese aus. Alle ihre Abmessungen sind gleich wie die der originalen Standardfeder. Ihre besseren Daten sind in der Legende zu Abb.11 und in der Anmerkung 6 genannt.
Die zwei Umlenkungen für den Faden sind fixe Erichtungen (Kanten). Damit sie dem Hebel nicht im Wege stehen, ist dieser zweiarmig ausgeführt. Seine beiden Arme können die Umlenkungen außen passieren. Der Faden ist mittig auf dem Quersteg der Arme befestigt und wird auf die mittig auf dem Fahrgestell montierten Umlenkkanten abgelegt (Gleiten des Fadens auf je einem Stück Fahrradspeiche, Anmerkung 7).
 Abb.13 Mausefallenauto #2: Seiten- und Draufsicht; Doppelhebel, nicht gespannt; Fadenlauf über 2 Umlenkkanten
Abb.13 Mausefallenauto #2: Seiten- und Draufsicht; Doppelhebel, nicht gespannt; Fadenlauf über 2 Umlenkkanten
 Abb.14 Mausefallenauto #2:
links: Mausefalle mit stärkerer Schenkelfeder und Schlitz für Anschluss der Fadenumlenkung rechts: Vorgelegegetriebe vor der Hinterachse, blockiert mit Holzplättchen; Doppelhebel, gespannt
Abb.14 Mausefallenauto #2:
links: Mausefalle mit stärkerer Schenkelfeder und Schlitz für Anschluss der Fadenumlenkung rechts: Vorgelegegetriebe vor der Hinterachse, blockiert mit Holzplättchen; Doppelhebel, gespannt
 Abb.15 Mausefallenauto #2: Details an der Hinterachse;
links: CD als linkes Hinterrad, von oben: Doppelhebel (gespannt), Vorgelegewelle mit kleinem Kugellager und Fadenwickel, Radwelle mit größerem Kugellager (befestigt mit Gummiband) rechts: CD als rechtes Hinterrad, von links: Doppelhebel (gespannt), Zahnräder (blockiert mit Holzplättchen), Lagerstellen (mit Gummiband umschlossen)
Abb.15 Mausefallenauto #2: Details an der Hinterachse;
links: CD als linkes Hinterrad, von oben: Doppelhebel (gespannt), Vorgelegewelle mit kleinem Kugellager und Fadenwickel, Radwelle mit größerem Kugellager (befestigt mit Gummiband) rechts: CD als rechtes Hinterrad, von links: Doppelhebel (gespannt), Zahnräder (blockiert mit Holzplättchen), Lagerstellen (mit Gummiband umschlossen)
Für das Anbringen des größeren Zahnrads des zugefügten Vorgeleges mussten zwei "Lagerböcke" für die Vorgelegewelle auf die Holme des Fahrgestells geklebt werden, weil diese dort an der Unterseite mit einer Traverse bei Baubeginn (Auto #1) verbunden worden waren. Für die Zahnräder gab es keine Zeitverzögerung infolge Beschaffung. Ich hatte Räder mit Modul m=1 für die Übersetzungen 2:1, 3:1 und 5:1 vorrätig.
Der Faktor 3 der gewählten Übersetzung 3:1 ins Schnelle ist zwar größer als das Verhältnis der Energieinhalte der aufgezogenen besseren und der aufgezogenen Standard-Feder, wurde aber vorgesehen, weil die Energieausnutzung durch die zweite Fadenumlenkung besser sein wird. Das Energie-Verhältnis entspricht den Flächen unter der Hebelkraft-Kurve und ist 7,5/3,5 = 2,14 (siehe Abb.n 10 und 11). Eine geringe Erhöhung der Antriebskraft ergibt sich daraus, dass der Hebel bisher 44cm, jetzt aber nur 42 cm lang ist (Differenz entspricht in etwa dem Abstand zwischen Vorgelege- und Radachse).
6.3 Fahrversuche und -ergebnisse
Mit dem Vorgelege-Getriebe (Hebel an der Mausefalle aber leicht kürzer) war die angetriebene Fahrstrecke von 48 Metern auf 137 Meter vergrößert worden. Diese Distanz erreichte ich ziemlich genau im Vorversuch ohne Fadenumlenkung (trotz vieler Wendemanöver, s.u.). Das Schnellerwerden durch die am Ende größere Fadenkraft und insbesondere der kurzzeitige Stoß nach Hebelstillstand waren deutlich erkennbar. Das Entspannen des gedehnten Fadens und der gebogenen Vorgelegewelle bewirkten, dass das Auto antriebslos noch über etwa 7 Meter weiterrollte.
Beim Fahren mit der aufgesetzten Fadenumlenkeinheit (2 Umlenkstellen) blieb das Auto nach dem Ende des Hebeldrehens i.d.R. sofort stehen (kein Nachlaufen). Es fuhr infolge des durch die Umlenkungen auf 102 cm verlängerten auf-/ und abgewickelten Fadens dennoch wesentlich weiter. Die konstruierte angetriebene Fahrstrecke betrug etwa 167 Meter (137m·102/82). Erreicht wurden 164 Meter (mögliche Quellen für den Unterschied sind Ungenauigkeiten beim Neuaufstellen des Autos bei 34 Wendemanövern auf der viel zu kurzen Teststrecke, der nicht genau bekannte Wickeldurchmesser des Fadens auf der Vorgelegewelle u.a.).
Unser Wohnzimmer war auch wegen seines nicht ganz ebenen Parketts keine ideale Teststrecke. Das Auto musste in der Mitte über einen kleinen Berg fahren, hat es aber immer mit Ach und Krach geschafft.
7. Schlußbemerkungen
Das Mausefallenauto hat durch den Eingriff technisch versierter Eltern und anderer Techniker die Unterrichts- und Werkstuben der Schulen verlassen. Diese Techniker haben ihm eine Behandlung angedeihen lassen, wie sie Präzisionsinstrumenten wie z.B. mechanischen Uhren zukommt. Dabei können sie die Lehrer als Initianten der Mausefallen-Wettbewerbe und hoffentlich auch die Schüler darauf aufmerksam machen, dass sie ein gut entwickeltes Gebiet angewendeter Naturwissenschaft betreten haben, dessen Erkenntnisse streng anzuwenden sind, um Erfolg im Wettbewerb zu haben. Für mich überwiegt allerdings der Eindruck, dass die Schüler zwar immer Spaß und Freude an ihren Entwürfen, aber oft nur zufällig Erfolg hatten und ihnen die sachlichen Gründe dafür unklar blieben. Die Rekorde stellten Erwachsene auf.
Die Technik der Schnellfahr-Mausefallenautos hat eine Parallele in der konventionellen Waffentechnik (keine Feuerwaffen): Die bereit gestellte mechanische Energie ist in kürzester Zeit in kinetische Energie umzuwandeln. Sowohl das Geschoss als auch das Auto sind schnellstens auf hohe Geschwindigkeit zu beschleunigen.
Das Weitfahr-Mausefallenauto ist mit einer mechanischen Uhr vergleichbar: Die bereit gestellte mechanische Energie hat die Uhrzeiger über eine möglichst lange Zeit in Bewegung zu halten. Das Auto hat möglichst lange Zeit und möglichst weit zu fahren. Es muss nur minimal beschleinigt werden.
Die anzuwendete Präzision dient dazu, Energieverluste durch Minimieren der Reibungen zu verkleinern. Die Uhren sind meistens relativ klein, sodass ihre Herstellung zusätzlich Präzision erfordert. Beim vergleichsweise weniger kleinen Auto steht der Leichtbau im Vordergrund (im Extrem < 100 Gramm). Ein leichteres Auto erfährt geringeren Reibungsverlust beim Rollen auf der Fahrbahn. Durch den Leichtbau wird das Auto zerbrechlich, ist somit kein leicht zu handhabender Gegenstand. Bei der Uhr spielt das weniger eine Rolle: Sie muss sich nicht fortbewegen. Es sind nur die Zeiger zu drehen. Damit sie sich sicher drehenn können, werden sie von einem Uhrenglas abgedeckt.
Bei einer Uhr haben auch Umgebungsbedingungen wenig Einfluss (bei einer sogenannten Jahresuhr wird zusätzlicher Luftwiderstand des Drehpendels infolge Luftzug vermieden, indem die Uhr unter eine Glasglocke gestellt wird). Beim Mausefallenauto haben Ebenheit und Festigkeit der Fahrbahn entscheidenden Einfluss. Für Weitfahrrekordversuche wird immer noch eine Fahrbahn gesucht, die genau horizontal und glatt ist und auch keinen geringsten "Hügel" aufweist. Schul-Tunhallen erfüllen diese Bedingungen nicht. "Ich sollte mit dem Auto anfangen, Böden zu vermessen. Genauer kann das sonst wahrscheinlich keine Messmethode." [Raschke: Auto 3, 7.4.2019].
Das weniger oft gebaute Mausefallen-Einachsauto hat wegen der Reduktion der Räder von wenigstens drei beim Zweiachsauto auf nur zwei Räder geringeren Rollwiderstand. Die bisher größte Fahrweite wurde mit solch einem Auto erreicht: über 400 Meter [Raschke: Auto 6].
8. Anmerkungen:
Anmerkung 1: Der Texaner Alden J. Balmer hat für Weitfahrwettbewerbe diese Regulations aufgeschrieben.
Anmerkung 2: Die Drehmomentwerte Mvor und Mmax der käuflichen Mausefallen-Federn scheinen zu schwanken. Raschke berichtet von einer stärkeren Falle als es meine sind: mehr als doppelt so stark vorgespannt und mit einem Viertel höherem Maximalwert: 7,5N/2,5N. Die von mir gefundenen schwächeren Ausführungen sind ihm aber auch begegnet. Fallen mit etwa den von mir bestimmten Daten wurden von der Schule seines Sohnes den Schülern für den dort geplanten Wettbewerb abgegeben: 5,7N/0,6N .
Anmerkung 3: Die elastische Verformungen des Fadens und der Antriebswelle gehen nicht verloren, denn sie werden am Schluss wieder in einen kleinen Antriebs-Stoß umgewandelt. Verloren ist aber die Energie, die den (elastischen) Stoß des Hebels auf seinen Anschlag bewirkt.
Anmerkung 4: Es handelt sich um die sogenannte Theorie erster Ordnung bzw. erster Näherung. Die Gleichgewichte zwischen Kräften und Momenten werden am unverformten Balken bilanziert, und es gilt die Annahme, dass die gegenseitig verdrehten Querschnitte jeder für sich eben geblieben sind.
Anmerkung 5: Das Beispiel des "Freiträgers", der am freien Ende A anstatt mit einer Kraft F mit einem Drehmoment M0 (wirkt konstant über ganze Länge) beansprucht wird, ist auch sehr anschaulich. Die Formel (4) für seinen Verdrehwinkel am freien Ende ist identisch mit der Formel (3b) für die Verdrehung der Schenkelfeder:
φA = M0·l / (E·J), (4) ,
φA = M0·l / (E·J), (3b) .
(3b) entstand durch Ersetzen von F·r in (3a) durch M0. Aus Gleichheitsgründen kann φ bedenkenlos der Index A angehängt werden, denn der Schenkel wird als relativ starr betrachtet, und dieser φ-Wert gilt für seine ganze Länge, also auch für sein äußeres Ende.
Letztlich ist aber doch die Schenkelfeder ein anschaulicheres Objekt. Die Schenkel als starr zu betrachten, was einfacher ist als sich vorzustellen, wie man einen Träger mit einem konstanten Biegemoment belastet. Aus gutem Grund wird in Verbindung mit letzterem Fall mit "reine" oder "querkraftfreie Biegung" ein Sonderbegriff benutzt.
Anmerkung 6: Die Darstellung bezieht sich auf eine Feder gleicher Abmessungen, für die lediglich Federstahldraht üblicher Festigkeit verwendet wird. Diese lässt sich auf einen fünf mal höheren Wert vorspannen und sicher bis 10N·42mm weiter spannen.
Anmerkung 7: Zum Beibehalten nur eines Hebelarms wäre ein seitlicher Ausleger für die Befestigung des Fadens an ihm anzubringen. Wegen des durch die Fadenkraft verursachten Torsionsmomentes müsste der Hebelarm verstärkt um nicht tortiert zu werden, was etwa gleich viel zusätzliche Masse bedeutet wie ein zweiter Hebelarm. Aus Symmetriegründen bevorzuge ich den Symmetriegewinn durch die Hebelverdopplung.
9. Nachtrag
"Kurvenscheibe" (Ecken-Hebel) anstatt geraden Hebel (Standard-Hebel)
(August 2020)Eine "Kurvenscheibe" anstatt eines geraden Hebels wurde u.a. schon von Raschke angewendet: Abb.16. Ich beschäftige mich theoretisch (geometrische Zusammenhänge und Konstruktion, keine Anfertigung) mit dieser Lösung und hänge meine Gedanken und Vergleiche zur Lösung mit geradem Hebel als Nachtrag an.
 Abb.16 Mausefallenwagen mit "Kurvenscheibe" [Raschke: Kurvenscheibe] von links nach rechts: Wirksame Hebellänge (rot) wird beim Rückdrehen der Mausfalle fortlaufend kleiner.
Abb.16 Mausefallenwagen mit "Kurvenscheibe" [Raschke: Kurvenscheibe] von links nach rechts: Wirksame Hebellänge (rot) wird beim Rückdrehen der Mausfalle fortlaufend kleiner.
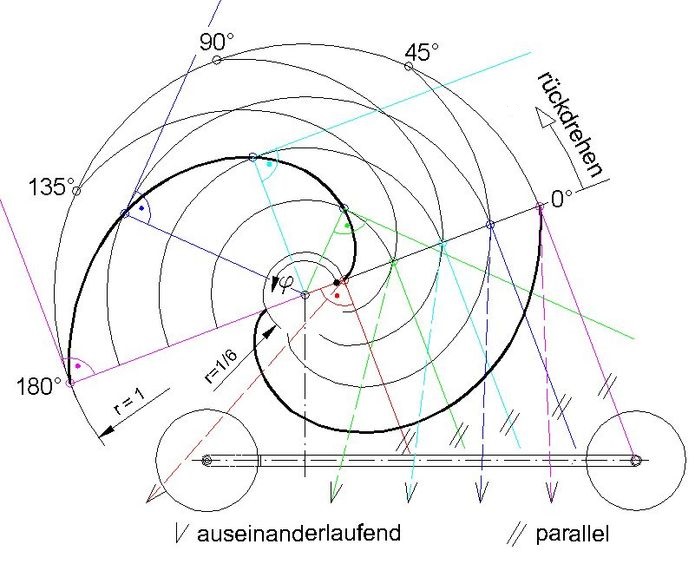 Abb.17 Kurvenscheibe ähnlich einer Archimedischen Spirale
Abb.17 Kurvenscheibe ähnlich einer Archimedischen Spirale
Die Forderung nach einer Folge von (wirksamen) Hebeln mit sich proportional zum Drehwinkel ändernder Länge führt zu eine Kurve, die ähnlich einer
Archimedischen Spirale ist. Der Radius r eines Punktes auf ihr wächst bei einer Drehbewegung proportional zum Drehwinkel φ. Im Unterschied zur originalen Archimedischen Spirale ist dem Radius der geforderten Spirale ein konstanter Wert hinzuaddiert (sie beginnt bei φ = 0 nicht mit r = 0 sondern mit r = 1/6, wobei sich der Wert 1/6 aus der Kennlinie der Feder 6|1 ergibt).
Diese Spirale ist aber für den vorliegenden Zweck nicht unmittelbar brauchbar:
1. Könnten die von den Radiuspfeilen senkrecht wegführenden Geraden den Zugfaden repräsentieren, müssten sie in allen Drehstellungen der Spirale aufeinander liegen, um zu einem gemeinsamen Punkt (auf der Radwelle oder eine vorgeschalteten Welle, von der der aufgewickelte Faden abgezogen wird) zu führen. Sie sind aber lediglich untereinander parallel (siehe Abb.17, rechts unten).
2. Als Zugfaden kommt nur ein auf die Spirale aufgewickelter Faden infrage (die Überlegungen in 1. sind hinfällig). Am Abhebepunkt von der Spirale ist dessen Richtung die der Tangente an diesem Punkt. Da die Steigung der Spirale nicht konstant ist, sind die Tangenten bei verschiedenen Drehstellungen nicht einmal parallel, sondern sie laufen auseinander (siehe Abb.17, unten). Somit ist auch das Verhältnis zwischen Radiuspfeil und wirsamer Hebellänge auf der Spirale nicht konstant.
In Abb. 18 ist die im Detail wiederholte Konstruktion der in Abb.16 gezeigten "Kurvenscheibe", die ich im Folgenden als Eckenhebel bezeichne, dargestellt. Ihre Ausformung als Scheibe mit sich stetig verändernder Kontur ist (wie später noch gezeigt wird) prinzipiell nicht möglich. Das war in der mit Abb.16 hingewiesenen Ausführung auch nicht angestrebt. Es handelt sich dort und im Folgenden um eine punktweise Näherung mit geraden Verbindungen zwischen Eck-Punkten.
In Abb.18 ist eine der abgewandelten Archimedischen Spirale aus Abb.17 ähnliche Kurve (blau) vergleichsweise enthalten, obwohl die konstruierte Polylinie (Eckhebelkontur, rot) von ihr eher mehr als weniger abweicht. Die Radiuspfeile der blauen Kurve (wirksame Hebel) werden rechtwinklig von Geraden (Faden, magenta) getroffen, die alle aus einem gemeinsamen Punkt (auf der Antriebswelle) kommen. Zu den Pfeilen (außer zum längsten, α =0°) gehört je ein größerer Winkel φ.
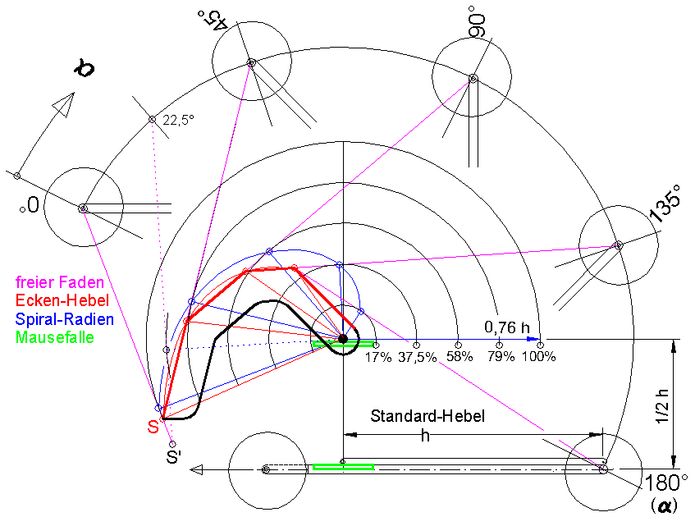 Abb.18 Konstruktion eines Ecken-Hebels (rot) für Mausefallenfeder (6|1): Seine End- und Eckpunkte stellen die Enden diskret verteilter realer Hebel dar. Der Zugfaden ist jeweils während eines Teils der Mausefallenrückdrehung quasi an einem dieser Stellen (Hebel) befestigt. Die blau gezeichneten Hebel sind fiktiv. Ihre Enden bilden eine Spirale, die der abgewandelten Archimedischen Spirale von Abb.17 ähnelt.
Abb.18 Konstruktion eines Ecken-Hebels (rot) für Mausefallenfeder (6|1): Seine End- und Eckpunkte stellen die Enden diskret verteilter realer Hebel dar. Der Zugfaden ist jeweils während eines Teils der Mausefallenrückdrehung quasi an einem dieser Stellen (Hebel) befestigt. Die blau gezeichneten Hebel sind fiktiv. Ihre Enden bilden eine Spirale, die der abgewandelten Archimedischen Spirale von Abb.17 ähnelt.Die Konstruktion des Ecken-Hebels kann nicht direkt vom geraden Standard-Hebel (Länge = h), dessen Spitze am Anfang (α =0°) direkt auf der Antriebswelle liegt, ausgehen. Wäre der längste Teilhebel des Eckenhebels mit diesem identisch, läge im Anfangsbereich des Winkels α diejenige unbefriedigende Situation (siehe Abschnitt 5.4) vor, die es zu vermeiden gilt. Der Ecken-Hebel ist kürzer als der Standard-Hebel (z.B. ≈ 3/4 h in Abb.18), und zwischen ihm und der Antriebswelle befindet sich auch am Anfang ein Stück frei liegender Faden. Letzterers ist als "Manövriermasse" erforderlich, um dem ablaufenden Faden stets die Richtung zur Antriebswelle hin erteilen zu können. Zu erfüllen sind lediglich diese beiden Maßnahmen (Hebel kürzer und freies Fadenstück). Eine quantitative Optimierung habe ich nicht vorgenommen, weil diese auch von der Federkennlinie und von der gewünschten Zahl der Hebel-Ecken abhängig ist. Sonst richtet sich die relative Lage des Eckenhebels (mit dem Mausefallenbügel drehend) auf dem Mausefallenauto nach den Platzverhältnissen (Kollision mit dem Auto-Chassis und mit der Fahrbahn vermeiden).
Konstruktions-Schritte (Abb.18):
1. Wahl der maximalen wirksamen Hebellänge (= 0,76 h).
2. Wahl der Verschiebung der Mausefalle mit Eck-Hebel nach oben (= 0,5 h, daraus folgt die Distanz zwischen dem Eck-Hebel-Drehzentrum und der Antriebswelle ≈ 1,12 h).
3. Wahl der Eckenzahl des Hebels (bzw. der Werte des Ablaufwinkels α = 0°, 45°, 90°, 135° und 180°; α =180° - φ).
4. Zeichnen der Kreise mit Radius = wirksame Hebellänge je Wert des Ablaufwinkels (für Mausefallenfeder 6|1 = 1,00- bis 0,17-faches von 0,76 h: die Distanz zwischen Eck-Hebel-Drehzentrum und Antriebswelle ist ungefähr das 1,47-fache der größten wirksamen Hebellänge: 1,12/0,76).
5. Tangenten zeichnen an die Kreise (4.) von der jeweiligen α-Winkelstellung der Antriebswelle aus. In der Konstruktionszeichnung ist das Drehen des zu erstellenden Winkelhebels eingefroren. Dafür ist die Antriebswelle rund um das Hebelzentrum verteilt dargestellt.
6. Die Schnittpunkte zwischen den jeweils benachbarten Tangenten (5.) sind die gesuchten Ecken des Ecken-Hebels.
Die Ecken-Punkte (6.) sind auf den Tangenten (magenta) über die Spiralen-Punkte (blau) hinaus verschoben, wobei die Verschiebung bei kurzen wirksamen Hebeln (blau) relativ größer ist. Am längsten Teilhebel ist die Verschiebung bis S am kleinsten. Diese wird aber größer (Verschiebung bis S'), wenn z.B. eine zusätzliche Ecke für α= 22,5° hinzukommt. Fügt man immer weiter zusätzliche Ecken ein, so nähert man sich einer stetig gekrümmten Kontur. Der Punkt S' rückt dabei ins Unendliche, was zeigt, dass ein stetig gekrümmter Hebel nicht möglich ist, weil er unendlich groß werden müsste.
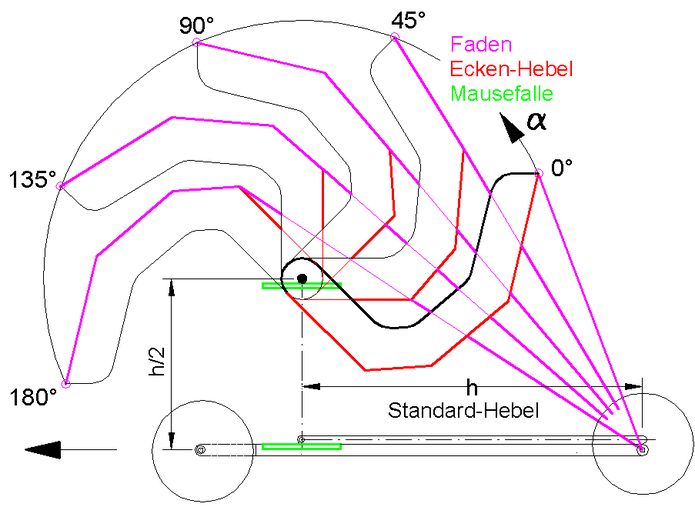 Abb.19 Ecken-Hebel in 5 Winkelstellungen α
Abb.19 Ecken-Hebel in 5 Winkelstellungen α
Wirkungsweise des Ecken-Hebels:
An den Ecken wird der Zugfaden fortschreitend von einem längeren auf einen kürzeren Einzelhebel übergeben (Abb.19). An den Ecken hat die Fadenkraft den gewünschten konstanten Wert. Im Bereich dazwischen wird sie gleich wie bei Verwendung des einzigen Standardhebels kleiner. Die Abweichung ist umso kleiner je mehr Ecken konstruiert wurden. Funktional besteht eine Parallele zur Fadenumlenkung über erhöhte Punkte (siehe 4.3; anstatt auf einem Eck-Hebel findet in Abb.13, oben eine Fadenübergabe an zwei festen Eckpunkten statt).
Der konstruierte Eckhebel hat zusammen mit seiner Spitze 4 wirksame Ecken, bei der Fadenumlenkung wirken einschließlich der Spitze des Standard-Hebels 3 Ecken. Dieser kleine zahlenmäßige Unterschied wiederholt sich beim Genauigkeitsvergleich:
Die Abweichung von der konstanten Fadenkraft beträgt beispielsweise beim Ecken-Hebel zwischen α = 0° und 45° maximal etwa -3,5% bzw.
zwischen α = 135° und 180° maximal etwa -5,3% (wirksamer Hebel zu lang, Fadenkraft zu klein; Zahlen gelten für Distanz zwischen Eck-Hebel-Drehzentrum und Antriebswelle als Wurzel-2-faches der größten wirksamen Hebellänge), was durchaus nicht wesentlich kleiner als die Abweichungen bei Fadenumlenkung (siehe Abb.n 10 bis 12) ist. Selbstverständlich kann die Eckenzahl ohne Weiteres verdoppelt oder vervierfacht und die Genauigkeit so auf einfache Weise noch weiter erhöht werden.
![]() Siegfried Wetzel, CH 3400 Burgdorf, Juni 2020 (Juli 20, Aug. 20)
Siegfried Wetzel, CH 3400 Burgdorf, Juni 2020 (Juli 20, Aug. 20)
↑ Anfang
<< andere Fahrzegtechnik-Beiträge
<< Home