<< Home
<< andere Fahrzeugtechnik-Beiträge

 ↓↓ Ende

Elastische Schienenbefestigung

Dieser Beitrag enthält einige mit Legenden versehene Fotos einer elastischen Schienenbefestigung mit der sogenannten Epsilonspannklemme. Dem ist eine überschlägige Federungsrechnung angehängt.

Zwei komplette Teile-Garnituren (eine für Holz-, die andere für Betonschwellen) fand ich in der Alteisenmulde der hiesigen Niederlassung der Gleisbaufirma Sersa.

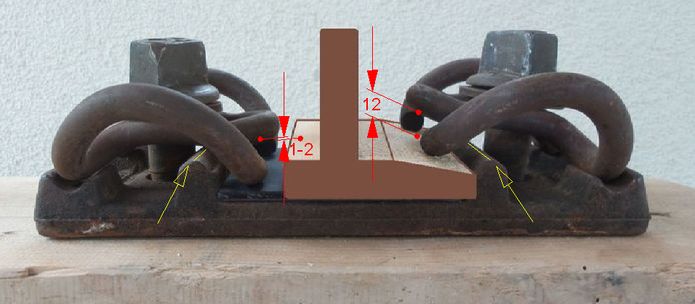Abb.1   Schienenbefestigung mit elastischen "Spannklemmen" auf einer Schwelle aus Holz
            Prinzip-Modell (hellbraun: Holzmodell einer Eisenbahnschiene, links und oben beschnitten)
            links: mittlere Öse der Klemme auf Anschlag (gelbe Linie); gegenüber Schienenfuß bestehen 1 bis 2mm Luft
            rechts: Klemme vor dem Eindrehen der Schienenschraube, mit der die Öse dann etwa 12 mm bis zum An-
                       schlag (gelbe Linie) herunter gedrückt wird (bis zum Schienenfuß werden 1 bis 2 mm Luft verbleiben)

Abb.2   Bauteile für die Schienenbefestigung mit elastischer "Spannklemme" auf einer Schwelle aus Beton
            links: Bausatz für eine Schienenseite inklusive Schraubendübel für Beton
                     (Ansicht der Schienen-zugewendeten Seite;
                     unten im Dübel vorstehender Holzpfropfen gegen aufsteigende Nässe, eigesteckt ins Aufstellbrett)
            rechts: diverse Ansichten der Metallteile (von links, von außen und von oben)

Bei den Betonschwellen ist der Bausatz für die Befestigung einer Schiene auf einer Schwelle zweiteilig. Es fehlt die bei Holzschwellen übliche metallene Auflageplatte. Die Schienen liegen mit ihrer dünnen elastischen Unterlage direkt auf der Schwelle. Die gegenseitige Positionierung der beiden Baugruppen erfolgt über die Schwelle, in deren Nuten die jeweilige Nase der einzelnen metallenen Platte eingreift.

Abb.3   Hälfte einer elastische Spannklemme:
            mit eingetragenen Anmessungen;
            für überschlägige Verformungsrechnung in
                                 gerade Abschnitte aufgeteilt

Diese Spannklemme wird seit nun mehr als 50 Jahren erfolgreich und in immensen Stückzahlen benutzt. Ihre Eigenschaften stehen im Detail längst nicht mehr zur Debatte. Wem sie dennoch interessieren, kann sie einschlägigen Produktinformationen entnehmen. Das tue ich auch und finde, dass die Klemme mit 9 kN Kraft 12 mm zusammen gedrückt wird. (System W 14 von Vossloh)
Mit dem folgenden Versuch, durch Anwenden der Verformungslehre des geraden schlanken Stabes die Federungsrate der Klemme überschlägig zu ermitteln, versetze ich mich in den in den 1960er Jahren tätigen Entwerfer dieses Bauteils. Ob dieser allerdings versuchte, die Eigenschaften dieses Teils, das fast nirgends aus geraden schlanken Stäben wenigstens zusammengesetzt ist, vorher zu sehen, bleibe dahingestellt. Denn sicher ist, dass es damals noch keine Rechenwerkzeuge (Finite-Elemente-Methode o.ä.) gab, mit denen man sich dem wahren Verhalten solcher "krummen Dinger" einigermaßen ausreichend gut nähern konnte. Näher liegt, dass man damals gleich einen oder mehrere leicht unterschiedliche Prototypen anfertigte und deren Federsteifigkeit durch Belastungsversuche ermittelte. Ich bin wunderlich und begehe den klassischen Rechenweg einmal.

Wegen ihres symmetrischen Aufbaus genügt es, dass die Berechnung für eine Hälfte der Klemme vorgenommen wird. In Abb.3 sind die sich verformenden Teile einer Klammerhälfte mit drei geraden, rot skizzierten Stücken (A, B und C) näherungsweise erfasst (mit Teil C bleibt zusätzlich eine Krümmung senkrecht zu Bildebene unbeachtet). Nahe am freien Ende von A wirkt von unten eine Kraft von 4,5 kN (9kN/2). C liegt etwa in seiner Mitte auf der Bodenplatte auf. Seine geringe Biegeverformung wird vernachlässigt, nur seine Torsion wird berücksichtigt. Unberücksicht bleiben auch die geringen Verformungen im mittleren, dem Ösenteil (Übergangsbereich schwarz skizziert) der Klemme. Der Teil B wird tortiert und gebogen, während Teil A nur gebogen wird.

Siegfried Wetzel, CH 3400 Burgdorf, Mai 2020, Juni 20

  ↑ Anfang

<< andere Fahrzegtechnik-Beiträge
<< Home