<< Home
<< andere Fahrzeugtechnik-Beiträge
↓↓ Ende
Elektrolokomotive:
Buchli-Antrieb (+ SLM-Universalantrieb)
und Antrieb mit "tanzendem Ring"
Inhalt
1. Einleitung2. Die Funktion des Buchli-Mechanismus
3. Anwendung des Buchli-Mechanismus (+ SLM-Universalantrieb)
4. Die Funktion eines Elektrolok-Antriebes mit "tanzendem Ring"
5. Anwendung des Elektrolok-Antriebes mit "tanzendem Ring"
1. Einleitung
Als Buchli-Antrieb wird eine besondere, von Jacob Buchli konstruierte Verbindung eines Elektromotors mit einem Triebrad einer elektrisch angetriebenen Lokomotive bezeichnet. Die Verbindung (Kupplung) geschieht nicht auf direktem Wege, sondern über einen Mechanismus, der das Auf- und Abfedern der Triebachse erlaubt, obwohl der relativ schwere Elektromotor auf dem Fahrgestell (Lokomotivkasten) fest montiert ist. Der Motor ist auf diese Weise nicht wie die Triebachse den vom Gleis ausgehenden Stößen und Schlägen ausgesetzt. Er ist den sogenannten gefederten Massen zugeschlagen, während die Triebachse eine sogenannte ungefederte Masse bleibt.
Von Straßenfahrzeugen kennt man dieses Prinzip und die zugehörenden Begriffe besser, da diese i.d.R. immer gefedert sind.
Der Buchli-Antrieb ist nur eine - wenn auch eine der bekanntesten - von mehreren Konstruktionen mit zwischen Fahrgestell bzw. Elektromotor radial frei beweglicher Kupplung.
Er gehört zu den sogeannten Gelenkantrieben ("Verzweigerantrieben"), was ein eisenbahntechnischer Begriff für solche Stab-Gelenk-Mechanismen bzw. Koppelgetriebe ist.
Als ein weiteres Beispiel eines "Verzweigerantriebes" wird nach dem Buchli-Antrieb ein Antrieb mit "tanzendem Ring" besprochen.
2. Die Funktion des Buchli-Mechanismus
Abb.1 drei Buchli-Antriebe an einer Elektrolok (SNCF 2D2 5516), mittlerer Antrieb ohne Verkleidungen, [Wikipedia]
![[Wikipedia]](https://upload.wikimedia.org/wikipedia/commons/3/3a/CdT_-_2D2_%C3%A9corch%C3%A9e.jpg){kind=link}
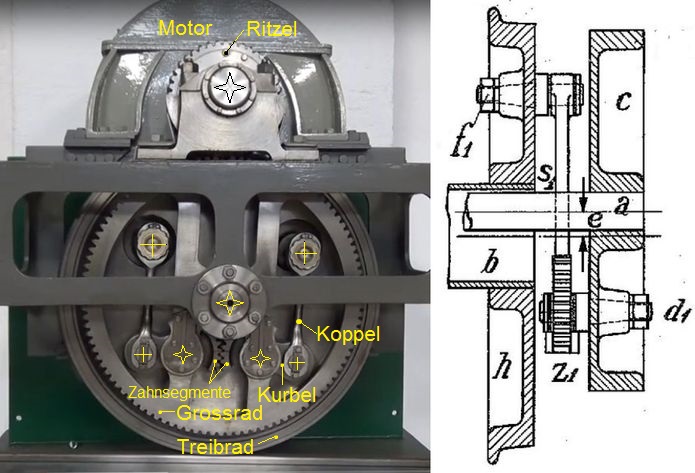Abb.2 1:5-Modell des BBC-Zahnsegmentantriebs (Buchli-Antrieb), Lok-Ausschnitt (SBB Ae 14/7), [Rudolf Hürlimann]
BBC = Brown, Boveri & Cie, Schweiz
Abb.3 Buchli-Antrieb: Zeichnung aus US-Patent (patentiert 1919), [US1298881]
c = Großrad (Zähne nicht gezeichnet); z = eine Kurbel mit Zahnsegment;
s = eine Koppel; h = Triebrad; a = Welle des Großrades; b = Hohlachse des Triebradsatzes;
e = halber möglicher Hub des Triebrades
Abb.4 Triebrad mit 2 Lagerbolzen für den Anschluß
der 2 Koppeln des außen liegenden
Buchli-Mechanismus und
Hohlachse mit Hublager-Innenteil ("Stein");
[R.Hürlimann]
↑ ↑ Abb.5 Triebrad, Außenseite
mit Lagerbolzen mit Kugelkopf; [R.Hürlimann]
Die beiden Räder (Trieb- und Großrad) liegen aufeinander, haben aber keine gemeinsame sondern je eine eigene Drehachse. Ihre parallelen Achsen bewegen sich radial gegeneinander, also in zwei Richtungen. Ihre zueinander relative Beweglichkeit hat den Beweglichkeits- oder Laufgrad F = 2. Die Großrad-Achse ist im Fahrgestell fix, während sich die Triebradachse auf- und abbewegt. Liegen die beiden Koppeln horizontal, so schwenken sie an den momentan unbewegten Kurbeln am Großrad auf und ab und ermöglichen so die vertikale Bewegung der Triebachse. In der anderen Sonderlage - die Koppeln liegen momentan vertikal - schwenken die Kurbeln am Großrad, und die Koppeln bewegen sich gemeinsam mit dem Triebrad auf und ab.
Beim Übertragen des Drehmomentes vom Großrad auf das Triebrad schiebt eine Koppel, und die andere zieht am Triebrad. Der Mechanismus hat aber ohne die gegenseitige Kopplung der Kurbeln eine zu große Bewegungsfreiheit. Er ist nicht zwangläufig, die Gestänge würden sich unkontrolliert bewegen. Die Verzahnung reduziert dieses zu viel an Beweglichkeit und führt zum Laufgrad F = 2. Der Laufgrad muss F = 2 sein, weil der Buchli-Mechanismus zwei Antriebe (an zwei verschiedenen Gliedern) hat: Das Großrad wird vom Motor angetrieben (gedreht), und das Triebrad wird von der Federung "angetrieben" (es wird auf- und abbewegt).
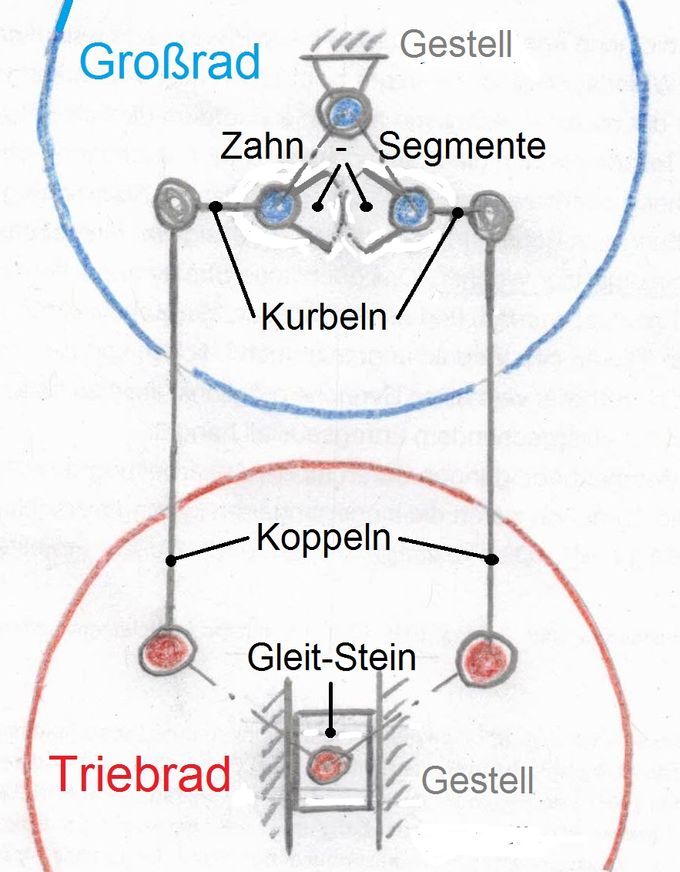Abb.6 Buchli-Mechanismus: Laufgrad-Bestimmung
formale Darstellung: Räder nebeneinander
Die Beweglichkeit in einem Mechanismus lässt sich mit einer Gleichung, nämlich der Grübler'schen Gleichung ausdrücken. Der gewünschte Laufgrad kann durch Anwenden dieser Gleichung kontrolliert werden.
Die Grübler'scheGleichung lautet für einen ebenen Mechanismus (ebenes Getriebe):
F = 3·(n -1 - g) + c + 2·d
n = Zahl der Glieder, g = Zahl der Gelenke,
c = Zahl der Gelenke mit Bewegungsfreiheit f = 1,
d = Zahl der Gelenke mit Bewegungsfreiheit f = 2.
Zahlen für den Buchli-Mechanismus:
n = 8 (Großrad, 2 Kurbeln, 2 Koppeln, Triebrad, Gleitstein, Fahrgestell),
g =10 (Fahrgestell/Großrad, Großrad/Kurbel (2x), Kurbel/Kurbel, Kurbel/Koppel (2x), Koppel/Triebrad (2x),
Triebrad/Gleitstein, Gleitstein/Fahrgestell),
c = 9 (alle Gelenke außer Kurbel/Kurbel),
d = 1 (Kurbel/Kurbel (f=2 = Gleiten+Schwenken zwischen den Zähnen)).
Kontrollrechnung:
F = 3·(8-1-10) + 9 + 2·1 = -9 +9 +2 = 2 ; F = 2 qed.
3. Anwendung des Buchli-Mechanismus (+ SLM-Universalantrieb)
Abb.7 SLM-Universalantrieb
Großrad innen zwischen den Triebrädern
in dessem Inneren eine sog. Kreuzkupplung
(Funktionspinzip: Oldham-Kuplung) [Wikipedia]
Der Buchli-Antrieb wurde in der ersten Hälfte des letzten Jahrhunderts gebaut und bis etwa zum Ende des Jahrhunderts benutzt. Mit seiner Hilfe wurden vorwiegend die von den Schienen herrührenden Stöße und Schläge von den Motoren schnellfahrender Loks - d.h. Reisezugloks - ferngehalten. Bei Fahrgeschwindigkeiten über 150 km/h wirkten sich aber die nicht gleichmäßig über den Umfang verteilt bleibenden Kurbeln und Koppeln im Mechanismus ungünstig aus. Diese ungleiche Massenverteilung führte wie eine fixe ungleiche Masseverteilung in rotierenden Körpern zu Unwuchten und war in der Folge davon eine Quelle unerwünschter Schwingungen. Eine diesbezügliche Verbesserung wurde mit dem sogenannten SLM-Universalantrieb" (Schweizerische Lokomotiv- und Maschinenfabrik; Abb.7), den ebenfalls Buchli entworfen hatte, erreicht.
In der Regel hatte jede Triebachse einen eigenen Antrieb (Einzelantrieb) mit Bucheli-Mechanismus. Dieser war meistens außerhalb des mit ihm gekoppelten Triebrads angebracht. Eine doppelte Abstützung der Großradachse durch die Triebachse hindurch wurde entgegen der Skizze in Abb.3 offensichtlich nicht vorgenommen (s. Abb.5: das Triebrad ist nicht durchbohrt). Das Großrad war fliegend gelagert.
Es gab aber auch innenliegende Buchli-Mechanismen, wobei das Großrad-Lager am Gestell sehr großen Durchmesser hatte, denn durch sein Zentrum führte berührungsfrei die vertikal schwingende Triebachse.
Es kam auch vor, dass von einem Motor aus beide Triebräder einer Achse mit Hilfe von zwei Mechanismen angetrieben wurden. Eine weitere Lösung waren zwei Motoren und zwei Mechanismen pro Triebachse. Wegen der Überbestimmtheit (zu kleiner Laufgrad) waren die Ritzel drehelastisch mit den Motoren verbunden.
Die Koppeln waren immer an beiden Enden mit Kugelgelenken angeschlossen, damit kein Verklemmen auftreten konnte, wenn die Triebachse sich gegenüber dem Gestell quer neigte. Der Mechanismus war somit immer ein räumliches Getriebe, nicht ein ebenes, wie in obiger vereinfachter Betrachtung. Die Grübler'sche Gleichung hat dafür die Form:
F = 6·(n -1 - g) + c + 2·d + 3·e
e = Zahl der Gelenke mit Bewegungsfreiheit f = 3 (mit 4 Kugelgelenken ist e = 4)
d = 2 (der Gleitstein gleitet und schwenkt senkrecht zur Gleitbahn)
c = 4 (5 weniger als vorher)
Kontollrechnung:
F = 6·(8-1-10) + 4 + 2·2 + 3·4= -18 +4 +4 + 12 = 2 ; F = 2 qed.
Eigentlich wären zwei im Mechanismus vorkommende sogenannte identische Bewegungsfreiheiten zu subtrahieren. Es sind überflüssige Freiheiten, die überflüssige Bewegungen einzelner Glieder gegeneinander ermöglichen. Die Beweglichkeit des Gesamtmechanismus wird davon nicht beeinflusst, weder erweitert noch eingeschränkt.
Diese identischen Bewegungsfreiheiten sind die möglichen Drehungen (natürlich nur innerhalb von Anschlägen innerhalb der Kugelgelenke) der Koppelstangen um ihre jeweilige Achse. Von den zusammen 12 Bewegungsfreiheiten der an den Koppeln angebrachten Kugelgelenke sind nur 10 erforderlich. Würde man sie nicht in der Kontrollrechnung nach Grübler beachten, wäre das Ergebnis F=0. Man hätte nichts gewonnen, denn erforderlich ist F=2. Eine Nachfrage beim übernächsten Nachfolger (inzwischen auch schon emeritiert) meines Lehrers Willibald Lichtenheld an der TU Dresden erbrachte die Bestätigung für meine Vermutung, dass sich die Grüblersche Gleichung auf räumliche Mechanismen nicht immer anwenden lässt. Sie ist scheinbar gültig, wenn die identischen Bewegungsfreiheiten nicht subtrahiert werden (siehe mein obiges qed.).
4. Die Funktion eines Elektrolok-Antriebes mit "tanzendem Ring"
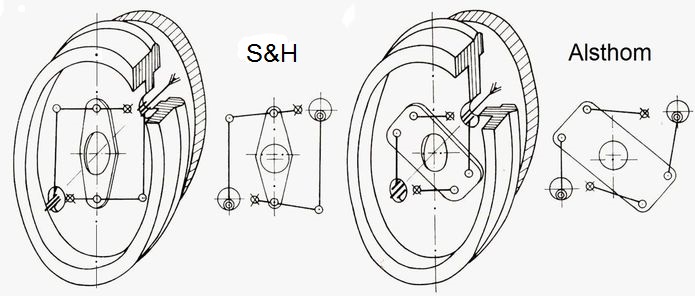Abb.8 zwei Entwürfe einer Kupplung mit "tanzendem Ring, [H. Bendel: Die elektische Lok,transpress,1994, S. 325]
links: die ursprünglich bei Siemens & Halske (S&H) entstandene Idee, 1890
rechts: die von Alsthom/F von S&H übernommene und weiterentwickelte, 1933
In den kleinen Bildteilen ist das Treibrad (vorne) eingefedert, es liegt höher als das Getriebe-Großrad (hinten).
Der Buchli-Antrieb wurde erstmals in den 1920er Jahren angewendet. Ein Antrieb mit "tanzendem Ring" wurde zwar schon in den 1890er Jahren entworfen, wurde aber erst in den 1930er Jahren gebaut und angewendet.
Bei der Verwendung des Buchli-Antriebs-Mechanismus waren die Achslager innerhalb der Räder auf der sie verbindenden Radsatzwelle angebracht. Der Raum außerhalb der Räder war frei, es standen auch keine Achsstummel vor. Der Mechanismus mit "tanzendem Ring" wurde immer bei üblicher, außerhalb der Räder erfolgten Lagerung der Achswelle verwendet, er musste die nach außen verlängerte Achswelle umgreifen. Aus diesem Grunde war aus dem durch die Mitte des Mechanismus führenden Stab eine Platte mit Loch oder ein Ring geworden. Er und seine tanzende Drehbewegung ergaben den Namen "tanzender Ring".
Der Mechanismus mit "tanzendem Ring" hätte sich auch auf der Innenseite der Räder befinden können. Die beiden Öffnungen in den Rädern wären entfallen. Um den Mechanismus aber leichter beobachten und reparieren zu können, wurde er außen angebracht. Beim Buchli-Antrieb war analog vorgegangen worden: Er befand sich ganz außen, und durch das außen befindliche Großrad ragten zwei Lagerbolzen. Beim Mechanismus mit "tanzendem Ring" befand sich das Großrad, innen und seine Radwelle war eine im Fahrgestell gelagerte, die federnde Achswelle umgreifende Hohlwelle.
Das treibende Getriebegroßrad und das getriebene, auf den Schienen laufende Rad sind durch Stab-Paare miteinandern verbunden. Ein Paar zieht, das andere schiebt das Laufrad; der verbindende "tanzende Ring" hält den Mechanismus zusammen, macht ihn zusammen mit Groß- und Laufrad zwangläufig. Hinzuzuzählen ist außer dem Fahrgestell noch die vertikale Geradführung eines Achslagergehäuses.
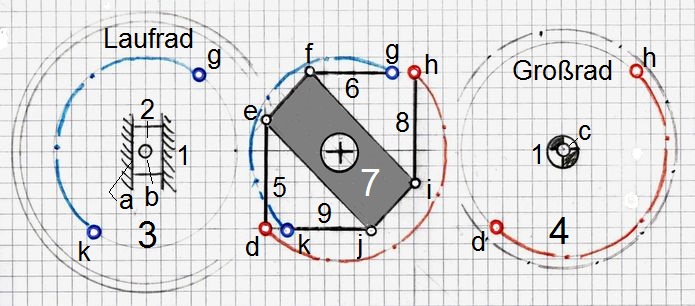Abb.9 Mechanismus mit "tanzendem Ring": Laufgrad-Bestimmung in formaler Darstellung (Räder nebeneinander)
n = Zahl der Glieder = 9 ("1" bis "9")
g = Zahl der Gelenke = 11 ("a" bis "k")
Laufgrad-Kontrolle mit Hilfe der Grüblerschen Gleichung:
F = 3·(n -1 - g) + c
n = Zahl der Glieder, g = Zahl der Gelenke,
c = Zahl der Gelenke mit Bewegungsfreiheit f = 1
Zahlen für den Mechanismus mit "tanzendem Ring":
n = 9 (Fahrgestell, Gleitstein, Laufrad, Großrad, 4 Stäbe, "tanz. Ring")
g = 11 (10 Drehgelenke, 1 Schubgelenk)
c = 11 (f = 1 in allen Gelenken),
Kontrollrechnung:
F = 3·(9-1-11) + 11 = -) + 11 = 2 ; F = 2 qed.
Für den Entwurf von S&H ist das Ergebnis der Rechnung gleich, denn die einzusetzenden Werte für n, g und c sind gleich. Die beiden Mechanismen unterscheiden sich nur dadurch, dass bei Alsthom der "tanzende Ring" 2 Gelenke mehr und die waagerechten Stäbe je 1 Gelenk weniger haben.
5. Anwendung des Elektrolok-Antriebes mit "tanzendem Ring"
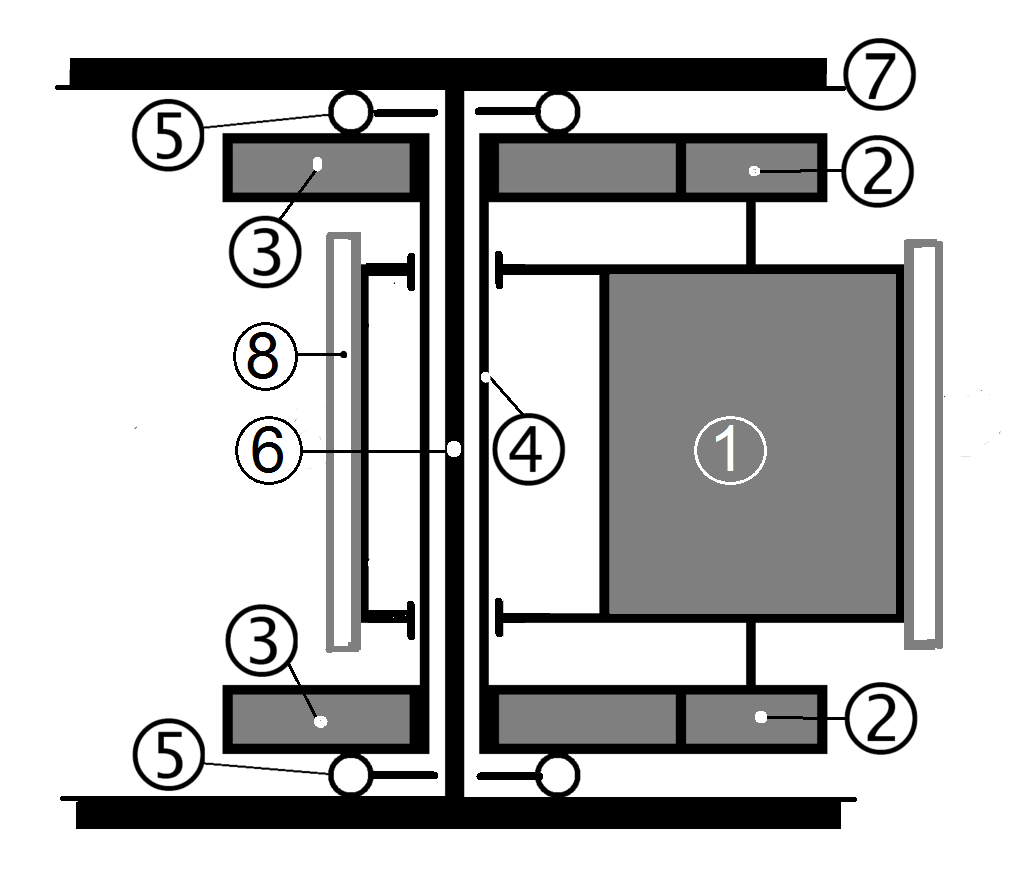Abb.10 Hohlwellen-Antrieb einer Elektrolok [Wikipedia]
(3) Großräder
(4) Hohlwelle
(5) radial bewegliche Kupplungen
(z.B. Mechanismen mit "tanzendem Ring")
Der Buchli-Antriebs-Mechanismus wurde fast ausschließlich immer nur an einer Seite der Achsen angebracht. Der Antriebs-Mechanismus mit "tanzendem Ring" wurde hingegen bei den französischen Staatsbahnen, die ihn fast ausschließlich anwendeten, wahrscheinlich immer doppelt benutzt. Die die federnde Achswelle umgreifende und mit dem Großrad verbundene Hohlwelle reichte von Rad zu Rad. Zur Aufnahme des zweiten Mechanismus mit "tanzendem Ring" wäre allerdings ein zweites Großrad oder ein entsprechendes Ersatzrad nötig gewesen. Das Schema in Abb.10 würde dem entsprechen.
Siegfried Wetzel, CH 3400 Burgdorf, November 2020 (Jan.21)
↑ Anfang
<< andere Fahrzegtechnik-Beiträge
<< Home