<< Home
<< andere Fahrrad-Beiträge
↓↓ Ende
Motor für Elektrofahrrad
Einleitung
Mit der Funktion des Motors eines Elektrofahrrads hat man sich selbst beim Nachrüsten im Eigenbau nicht auseinander zu setzen. Der Motor wird mit einer dem Bausatz beiliegenden elektronischen Steuerungseinheit bedient, und diese beeinflusst seinen Betrieb so, wie es für die Fahrbequemlichkeit und der Erfüllung gesetzlicher Bestimmungen erforderlich ist.
Mittlererweile gibt es Nachbausätze auch für das im Vergleich zum Einbau eines Nabenmotors grundsätzlich andere Antriebskonzept mit Mittelmotor und Drehmoment-Steuerung. Bisher kam der Mittelmotor inkl. Drehmomentsensor an der Pedalkurbel nur als eingebaute Einheit in kompletten Elektrofahrrädern auf den Markt. Ihr Fahrradrahmen weicht im Tretkurbelbereich wesentlich von der Standardform ab. Der Rahmen ist um die Antriebseinheit "herum gebaut" worden.
Zur Vorbereitung meines nächsten Nachrüst-Projekts beschäftigte ich mich zunächst mit den verschiedenen Steuerungskonzepten der verschiedenen Antriebsarten (3. Nachtrag (Okt.2015) in oben schon zitierter Arbeit). Diese besser zu verstehen führt unweigerlich dazu, sich auch mit der Funktion des Motors zu beschäftigen.
Die Funktion verstand ich mit Hilfe mehrerer Fachquellen, aus denen ich teilweise zitiere. Antworten auf ein paar darin nicht direkt besprochene Fragen füge ich für ein umfassenderes Verständnis (oder auch nur, weil ich zusätzliche Fragen hatte) bei.
1. Bürstenloser Gleichstrommotor
Die Leistung eines für Fahrräder gebrauchten Elektromotors ist relativ klein (< 1000 Watt), so dass das Erreger-Magnetfeld mit Permanentmagneten erzeugt werden kann. Damit lässt sich ein Gleichstromnebenschlussmotor (man ersetze die von IE durchflossenen Erregerspulen durch Permanentmagnete) zu einen konstant fremderregten bürstenlosen Motor machen (Abb.1). Seine elektrisch betriebenen Erregerpole werden von rotierenden Permanentmagneten ersetzt (Rotor). Die elektrisch betriebenen Hauptpole sind ruhend (Stator). Im Stator wird aus dem Gleichstrom eines Akkus ein umlaufendes magnetisches Hauptfeld durch elkronisches Kommutieren (Stromwenden: electronically commutated Motor, kurz EC-Motor) erzeugt.
Die Kennlinien variieren sehr stark mit der Drehzahl (Abb.2). Das bedeutet, dass der Motor in einem eingeschränkten Drehzahlbereich benutzt werden soll. Die Maxima von abgegebener mechanischer Leistung und elekto-mechanischem Wirkungsgrad haben eine verschiedene Drehzahl. Der günstige, beide Größen berücksichtigende Bereich liegt etwa zwischen 2/3 und 3/4 der Grenz-Drehzahl (Leerlaufdrehzahl).
Somit ist der Mittelmotor deutlich im Vorteil. Ein Nabenmotor dreht bei langsamer Fahrt viel zu langsam. Er verwertet die Akku-Energie schlechter; die Reichweite mit gleichem Energievorrat ist kleiner.
Die dem zum bürstenlosen Motor mutierten Nebenschlussmotor angelegte Akku-Spannung U fällt im Motor über der Stator(!)wicklung (R) ab und hebt die generierte Gegenspannung UG auf (Abb.3):
Ohne Generatorwirkung würde der Motor fortwährend elektrische Energie aufnehmen und wegen der geringen Reibung bis zu höchsten Drehzahlen beschleunigen und zerbersten.
Die Gegenspannung UGwächst wegen des konstanten Erregegerflusses Φ linear mit der Drehzahl n nach der Gleichung:
Mit Hilfe der Gleichungen (2) und (1) ergibt sich die Abhängigkeit der Drehzahl n vom Strom I:
In Abb.4 ist die Kennlinie nur in der Umgebung des vom Hersteller des Motors üblicherweise mit den Nennwerten IN und nN angegebenen Punkts gezeichnet.
Das vom Motor erzeugte Drehmoment M wächst wegen des konstanten Erregegerflusses Φ linear mit dem Strom I nach der Gleichung:
Der Strom ist diejenige physikalische Größe, mittels der der Motor gesteuert wird. Für die Anwendung des Motors als Antriebshilfe am Fahrrad interessieren aber unmittelbar das Drehmoment (insbesondere seine Abhängigkeit von der Drehzahl) und die mechanische Leistung (insbesondere ihr im Wirkungsgrad enthaltener Vergleich mit der elektrischen Leistung des Akkus). Die Abhängigkeit des Drehmoments von der Drehzahl ist in Abb.6 gezeigt. Die darin enthaltenen Formel wird mit Hilfe den Gleichungen (4) und (3) gefunden und lautet:
Die mechanische Leistung Nm eines rotierenden Körpers (Rotor) ist bekannterweise das Produkt aus Drehmoment M und Umfangsgeschwindigkeit ω = 2π·n (auf dem Einheitskreis, Rradius = 1).
Dass n2 = nL sein muss, ist auch ohne Nachrechnen offensichtlich: Bei n=nL ist M=0 (kein vom Motor abgegebenes Drehmoment bei Leerlauf, Abb.6) und damit Nm=0, denn Nm∼M·n .
Es interessieren noch die Drehzahl bei maximaler mechanischer Leistung und deren Wert bezogen auf die im Anfahrmoment aufgenommenen elektrischen Leistung.
Die erste Aufgabe
Zweite Aufgabe:
Die dem Motor entnommene mechanische Energie ist bei niedrigen Drehzahlen wesentlichtlich geringer als die zugeführte elektrische Energie. Der elektro-mechanische Wirkungsgrad η (Verhältnis zwischen abgegebener mechanischer und zugeführter elektrischer Energie oder zwischen mechanischer und elektrischer Leistung) ist nur wenig unterhalb der Leerlaufdrehzahl mit etwas mehr als 80% moderat. Beim Anfahren und Beschleunigen verhält sich der Motor wegen des dabei entstehenden großen Antriebs-Drehmoments günstig, was aber mit einem schlechten Wirkungsgrad einher geht. Der gleichzeitige hohe Strom erwärmt die Statorwicklungen übermässig. Elektrische Energie geht als Wärme verloren.
Die Gleichung für den Wirkungsgrad η lässt sich einfacher finden durch folgendes Umstellen der Gleichungen (5) bis (7):
(8) η(n) = n / nL .
Der Wirkungsgrad wächst linear mit der Drehzahl. Bei der Leerlaufdrehzahl nL nähert er sich theoretisch dem Wert 1 (100%). Abgesehen davon, dass in diesem Punkt kein Wirkungsgrad definiert werden kann (Division Null durch Null), ist die Proportionalität auch in der Nähe der Leerlaufdrehzahl nicht mehr gültig, weil die absoluten Werte der Leistung so klein geworden sind, dass die Reibungsverluste an der drehenden Welle nicht mehr wie in allen Betrachtungen bisher vernachlässigt werden können.
In der Literatur werden etwa 6/7 der Leerlaufdrehzahl für die Stelle des maximalen Wirkungsgrads angegeben. Die aus [2] übernommene, in Abb.2 gezeigte Kennlinie knickt in diesem Bereich aprupt ab. Für den damit beschriebenen Motor werden etwa 82% als ηmax angegeben.
[1a] elektronik-kurs.net: Betrieb von Gleichstrommotoren
Nachträglich fand ich in der LiteraturHinweise für die Einbeziehung der Reibungsverluste, was sich insbesondere auf die rechnerische Erfassung des Wirkungsgrads auswirkt [4],[5] . Damit eröffnete sich die Möglichkeit, Antworten für im Abschniit 2.7 in Bezug auf die Wirkungsgrad-Kennlinie in Abb.2 offen gebliebene Fragen zu finden.
Abb.6a Abhängigkeit des Drehmoments von der Drehzahl
Die Abbildungen 4a bis 6a sind die entsprechend korrigierten Diagramme aus den Abbildungen 4 bis 6.
Durch das Beachten des Reibungsmoments MR, ist zwischen elektomagnetisch erzeugtem Moment Melmag und an der Motorwelle nach außen abgegebenen MmechNutz zu unterscheiden.
Die an der Motorwelle nutzbare Leistung ist die Differenz aus elektromagnetisch erzeugter und Reibungsverlust-LeistungInhalt
2. Funktion eines Nebenschlussmotors (bürstenloser Gleichstrommotor)
2.1 Kennlinien: Leistung und Wirkungsgrad über Drehzahl
2.2 Ersatzschaltbild
2.3 Kennlinie: Drehzahl über Strom
2.4 Kennlinie: Drehmoment über Strom
2.5 Kennlinie: Drehmoment über Drehzahl
2.6 Kennlinie: mechanische Leistung über Drehzahl
2.7 Kennlinie: Wirkungsgrad über Drehzahl
3. Quellen
4. Nachtrag (Jan.2016)
4.1 Kennlinie der mechanischen Nutzleistung über der Drehzahl
4.2 Kennlinie des Wirkungsgrads über dem Strom
1. Bürstenloser Gleichstrommotor ↑
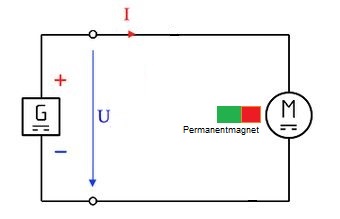 Abb.1 Schaltbild eines Nebenschlussmotors, [1b]
Abb.1 Schaltbild eines Nebenschlussmotors, [1b]
Erregerwicklung durch Permamentmagnet ersetzt
(M ∼ I2 anstatt nur M ∼ I; M=Drehmoment, I=Strom).
Für die Anwendung am Fahrrad kommt nur ein wartungsfreier Motor infrage. Ein Gleichstromreihenschlussmotor ist das aber nicht, denn er benötigt Kommutator-Bürsten, die gewartet werden müssen.
2. Funktion eines bürstenlosen Gleichstrommotors ↑
2.1 Kennlinien: Leistung und Wirkungsgrad über Drehzahl ↑
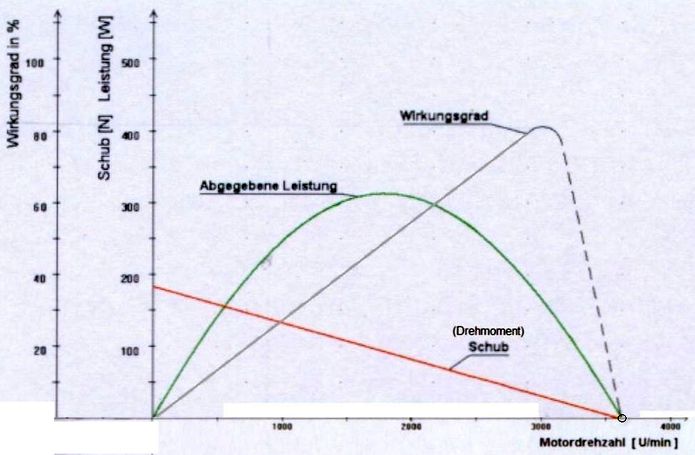 Abb.2 Kennlinien eines mit Permanentmagneten erregten Gleichstrommotors (bürstenloser Fahrrad-Motor), [2]
Abb.2 Kennlinien eines mit Permanentmagneten erregten Gleichstrommotors (bürstenloser Fahrrad-Motor), [2]
handelsüblicher Nabenmotor ohne Getriebe, 36 Volt, etwa 250 Watt Nennleistung
rote Kennlinie: zum Drehmoment (= Schub x Laufradhalbmesser) proportionale Schubkraft
2.2 Ersatzschaltbild ↑
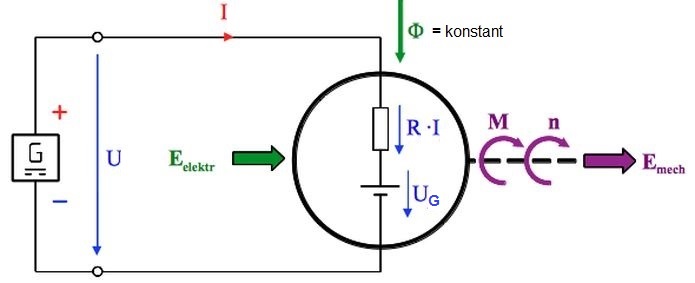 Abb.3 Ersatzschaltbild, [1a]
Abb.3 Ersatzschaltbild, [1a]
Erregung mit Permanentmagneten: Φ = konstant
(1) U = R·I + UG .
Sobald ein Elektromotor zu drehen begonnen hat, induziert er eine Gegenspannung, die schließlich bei der Grenz- oder Leerlauf-Drehzahl nL bis auf einen kleinen Rest den Wert der angelegten Spannung erreicht. Die Drehbeschleunigung des unbelasteten Motors ist jetzt beendet. Der noch fließende kleine Strom I dient zur Überwindung der kleinen Reibung im leer laufenden Motor.
Anmerkung: Die Gefahr zu hoher Drehzahlen besteht real bei der Steuerung von Gleichstromnebenschlussmotoren, wenn die Erregung zu stark verkleinert wird.
2.3 Kennlinie: Drehzahl über Strom ↑
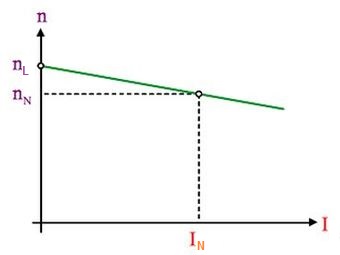 Abb.4 Abhängigkeit der Drehzahl vom Strom, [1a]
Abb.4 Abhängigkeit der Drehzahl vom Strom, [1a]
vernachlässigt ist,
dass bei nL noch ein kleiner Strom IL fließt.
(2) UG(n) = c·Φ·n = 2π·a·n .
Motor-Konstante c und Erregegerfluss Φ sind zur Konstanten a zusammen gefasst. Mit dem Faktor 2π wird der Gewohnheit Rechnung getragen, die Drehzahl n in U/min anstatt die Winkelgeschwindigkeit ω in rad/sec zu der die induzierte Gegenspannung proportional ist, zu verwenden.
Anmerkung: Die dimensionslose Maschinenkonstante c ist das Produkt aus den Zahlen der Stator(!)windungen und der Rotor(!)-Polpaare
(3) n(I) = (U - R·I) / (2π·a) .
(Akku-Spannung U ≈ konstant, Spulen-Widerstand R = konstant)
2.4 Kennlinie: Drehmoment über Strom ↑
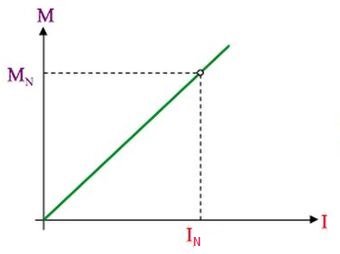 Abb.5 Abhängigkeit des Drehmoments vom Strom, [1a]
Abb.5 Abhängigkeit des Drehmoments vom Strom, [1a]
(4) M(I) = c·Φ·I = a·I .
Motor-Konstante c und Erregerfluss Φ sind zur Konstanten a zusammen gefasst (s.oben).
Der üblicherweise vom Hersteller des Motors mit den Nennwerten IN und MN angegebene Punkt befindet sich etwa in der Mitte des empfohlenen Arbeitsbereichs für die Drehzahl n.
2.5 Kennlinie: Drehmoment über Drehzahl ↑
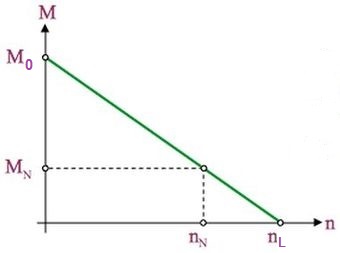 Abb.6 Abhängigkeit des Drehmoments von der Drehzahl,
Abb.6 Abhängigkeit des Drehmoments von der Drehzahl,
[1a]
(5) M(n) = (a / R)·(U - 2π·a·n) .
Dass das Anfahrts-Drehmoment M0 ein Vielfaches des Nenn-Drehmomentes MN ist, erweist sich als Vorteil beim Gebrauch des Motors an einem Fahrrad. Ein Nabenmotor dreht sich im Unterschied zu einem Mittelmotor bei langsamer Fahrt auch langsam. Das erhöhte Drehmoment sorgt dafür, dass die erforderliche mechanische Leistung vorliegt, allerdings ist der Wirkungsgrad während der gesamten Langsamfahrt-Phase schlecht. Beim Anfahren ist dieser auch schlecht, aber die Zeitdauer ist kurz, der Akku wird weniger überstrapaziert.
2.6 Kennlinie: mechanische Leistung über Drehzahl ↑
 Abb.2 Kennlinien eines mit Permanentmagneten erregten Gleichstrommotors (bürstenloser Fahrrad-Motor), [2]
Abb.2 Kennlinien eines mit Permanentmagneten erregten Gleichstrommotors (bürstenloser Fahrrad-Motor), [2]
handelsüblicher Nabenmotor ohne Getriebe, 36 Volt
rote Kennlinie: zum Drehmoment (= Schub x Laufradhalbmesser) proportionale SchubkraftKennlinie der mechanischen Leistung
Die Drehmoment-Gleichung (5) mit 2π·n multipliziert ergibt:
Nm = M · ω = (b / R) · (U - a·n) · 2π·n oder
(6) Nm(n) = (a·2π / R) · (U·n - 2π·a·n2) .
Das ist eine Gleichung zweiten Grades für Nm mit einer linearen und einer quadratischen Abhängigkeit von n.
Die Leistungskennlinie ist eine glockenformige Kurve, die bei n1 = 0 eine Nullstelle hat (beide Kurventeile - Gerade und Parabel - gehen durch den Koordinaten-Ursprung). Dass sie mit der Leistungskennlinie in Abb.2 (grüne Kurve) identisch ist, bedarf noch des Nachweises, dass ihre zweite Nullstelle bei n2 = nL liegt:
Nm = 0 = (a·2π / R) · (U·n2 - 2π·a·n22) → n2 = U / (2π·a)
Bei Leerlauf nL ist der Strom I (fast) Null. Mit I=0 in Gleichung (3) ist: n(0) = nL = U / (2π·a) .
→ n2 = nL, qed.Maxium der mechanischen Leistung
ist eine Extremwertaufgabe: Man differziere Gl. (6) nach der Drehzahl. Das Maximum befindet sich dort, wo der Differentialquotient eine Nullstelle hat.
d (Nm(n)) / dn = d ( (a·2π / R) · (U·n - 2π·a·n2) ) / dn = (a·2π / R) · (U - 2·2π·a·n) = 0
U - 2·2π·a·n = 0 >>> n1 = U / (4π·a)
Aus Gl. (3) folgt mit I=0 >>> nL = U / (2π·a) >>> n1 = nL / 2 .
Die maximale mechanische Leistung wird bei halber Leerlaufdrehzahl abgegeben.
Aus Gl. (6) folgt mit n = n1 = U / (4π·a) >>> Nmmax = (a / R) · ((U·nL/2) - (2π·a·nL2 / 4)) >>> Nmmax = U2 / 4·R
Die maximale elektrische Leistung wird im Anfahrmoment (n=0), wenn noch keine Gegenspannung UG generiert ist, aufgenommen und von der konstanten Motorspannung U und dem Widerstand R der Ankerwicklung bestimmt
(s. auch Gl.7):
Ne0 = U2 / R >>> Nmmax = Ne0 / 4 .
Die maximal abgegebene mechanische Leistung ist ein Viertel der im Anfahrmoment aufgenommenen elektrischen Leistung.
2.7 Kennlinie: Wirkungsgrad über Drehzahl ↑
Die elektrische Leistung Ne ist das Produkt aus Spannung U und Strom I:
Ne = U · I
Sie ist nur vom Strom abhängig, was durch Übernahme der nach dem Strom aufgelösten Gleichung (3)
(3.1) I = (1/R) · (U - a·n)
darstellbar ist:
(7) Ne(n) = U · I = (U/R) · (U - a·2π·n) .
Da die Akku-Spannung U annähernd konstant ist, und der Strom I wie das zu ihm proportionale Drehmoment M mit steigender Drehzahl linear fällt (Abb.6), ist die elektrische Leistung Ne(n) ebenfalls eine fallende Gerade.
a) Einführen der Werte bei Stillstand (Drehzahl n = 0): M0, Nm0 bzw. Ne0,
b) Bezug der Drehzahl auf die Leerlaufdrehzahl nL: n/ nL
(5.1) M(n) = M0·(1 - (n/nL))
← M(n) = (a / R) · (U - a·2π·n)
(6.1) Nm(n) = M0·(1 - (n/nL))·2π·n
← Nm(n) = (a·2π / R) · (U·n - a·2π·n2)
(7.1) Ne(n) = Ne0·(1 - (n/nL)) ← Ne(n) = (U/R) · (U - a·2π·n)
η-Quotient: Gl.(6.1) / Gl.(7.1)
η(n) = Nm(n) / Ne(n) = M0·(1 - (n/nL)·2π·n / (Ne0·(1 - (n/nL))
η(n) = M0·2π·n / Ne0
aus Gleichungen
Gl.(4): I = I0 → M0 = a·I0 .
Gl.(5): M = 0 → U / (a 2π) = nL .
Gl.(7): n = 0 → Ne0 = U·I0 .
η-Quotient:
η(n) = a·I0·2π· n / (U·I0) .
3. Quellen ↑
[1b] elektronik-kurs.net: Betriebsverhalten von Gleichstrommotoren
[2] Teja und Eberhard Müller: E-Bike-Technik, Books on Demand, 2011
[3] Uni Stuttgart, Institut für Leistungselektronik und Elektrische Antriebe:
Grundlagenpraktikum - Die Gleichstrommaschine
Nachtrag (Jan.2016):
[4] Germar Müller, Bernd Ponick: Theorie elektrischer Maschinen, WILEY-VCH, 2009
[5] Hans-Gerd Finke: Kenngrößen von Gleichstrommotoren
4. Nachtrag (Jan.2016) ↑
Von vorn herein werden in guter Näherung als konstant annehmbare Reibungsverluste berücksicht. In die Rechnung gehen sie als Reibungsmoment MR und als der dafür erforderliche Leerlaufstrom IL>0 ein, beides drehzahlunabhängig [4].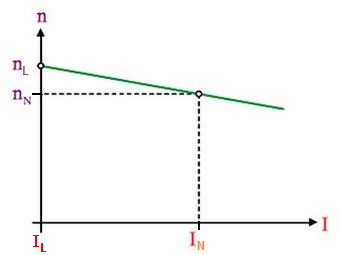
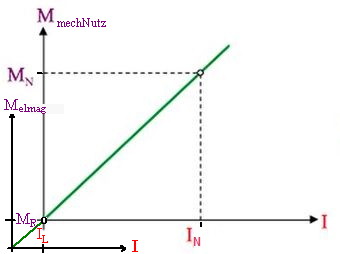 Abb.4a Abhängigkeit des Drehmoments von der Drehzahl Abb.5a Abhängigkeit der Drehzahl vom Strom
Abb.4a Abhängigkeit des Drehmoments von der Drehzahl Abb.5a Abhängigkeit der Drehzahl vom Strom
Mit dem Index elmag werden die Gleichungen (4) bis (6) zu den Gleichungen (4a) bis (6a).
Durch Beachten des Reibungsverlustes kommen mit dem Index R die Gleichungen (5b) und (6b) hinzu.
(4a) Melmag(I) = a·I ,
(5a) Melmag(n) = (a / R)·(U - a·2π·n) ,
(5b) MR = (a / R)·(U - a·2π·nL) .
(6a) Nelmag(n) = (a·2π / R) · (U·n - a·2π·n2) ,
(6b) NR = (a·2π / R) · n·(U - a·2π·nL)
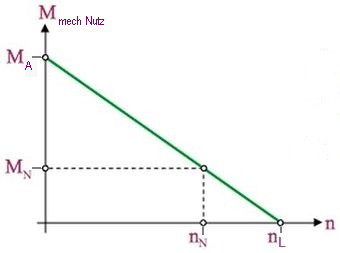
4.1 Kennlinie der mechanischen Nutzleistung über der Drehzahl ↑
Kennlinie der mechanischen Nutzleistung
NmechNutz(n) = Nelmag - NR ,
(6c) NmechNutz(n) = (a·2π / R) · ( (U·n - a·2π·n2) - n·(U - a·2π·nL) )
= ( (a·2π)2 / R) · ( nL·n - n2 ).
Maxium der mechanischen Nutzleistung
Es interessieren noch die Drehzahl nex bei maximaler mechanischer Nutz-Leistung und deren Wert bezogen auf die im Anfahrmoment aufgenommene elektrische Leistung.
Die erste Aufgabe
ist eine Extremwertaufgabe: Man differziere Gl. (6c) nach der Drehzahl. Das Maximum befindet sich dort, wo der Differentialquotient eine Nullstelle hat.
d (NmechNutz(n)) / dn = d ( ((a·2π)2 / R) · ( nL·n - n2 ) ) / dn = ((a·2π)2 / R) · (nL - 2·n) = 0 >>> nL - 2·n = 0
n1 = nL / 2
Die maximale mechanische Leistung wird bei halber Leerlaufdrehzahl abgegeben (kein prinzipieller Unterschied zum Fall ohne Berücksichtigung einer Reibleistung).
Zweite Aufgabe:
Aus Gl. (6c) folgt mit n = n1 = nL/2 :
NmNmax = ( (a·2π)2 / R) · ( nL·nL/2 - nL2/4 ) = ( (a·2π·nL)2 / R) · ( 1/2 - 1/4 ) = (a·2π·nL)2 / (4·R) .
Gemäß Gl. (3) gilt für den Leerlauf a·2π·nL = U - R·IL, somit wird
NmNmax = (U - R·IL)2 / (4·R) = (U2 / 4·R) · (1 - R·IL/ U)2 = (U2 / 4·R) · (1 - IL/ I)2 ,
Die im Anfahrmoment aufgenommene elektrischen Leistung ist Ne0 = U2 / R . Also gilt
NmNmax = (Ne0 / 4 ) · ((1 - IL/ I)2 .
Die maximal abgegebene mechanische Leistung ist etwas kleiner als ein Viertel der im Anfahrmoment aufgenommenen elektrischen Leistung.
4.2 Kennlinie des Wirkungsgrads über dem Strom ↑
Kennlinie des Wirkungsgrads
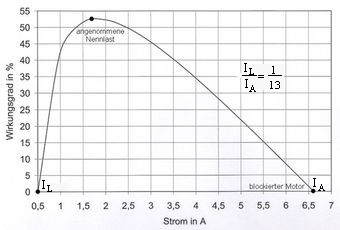
 Abb.7 Kennlinie: Wirkungsgrad über Strom Abb.2
Abb.7 Kennlinie: Wirkungsgrad über Strom Abb.2
eines in [5] beschriebenen Spielzeug-Motors
(Nennleistung etwa 10 Watt)
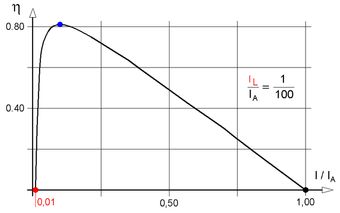
Abb.8 Kennlinie Wirkungsgrad über Strom, IL/IA = 1/100
Die über dem Strom aufgetragene Kennlinie (Abb.7) ist in etwa mit der an einer vertikalen Linie gespiegelten, über der Drehzahl aufgetragenen Kennlinie (Abb.2) identisch. Die Umrechnung zwischen beiden erfolgt mit Gl. (3):
fallende Gerade n(I), s. Abb. 4.
Für den direkten Vergleich mit Abb.7 wird im Folgenden die Gleichung des vom Strom abhängigen Wirkungsgrads hergeleitet (bereits in Abb.8 dargestellt).
Zuerst sind die im Wirkungsgrad aufeinader bezogenen Leistungsgleichungen als Funktionen des Stroms herzuleiten.
Die Herleitung des für die mechanische Nutzleistung nötigen Moments geht von Gl.(4) aus:
(4) M(I) = a·I Melmag(I) = a·I MR = a·IL.
Damit wird
MmechNutz = Melmag- MR zu MmechNutz = a·(I - IL).
Die mechanische Leistung ist:
NmechNutz = 2π·n·MmechNutz = 2π·n·a·(I - IL)
Aus den Gl.n (1) und (2) und mit U = IA·R >>>> 2π·n·a = R·(IA - I) . Und weiter:
N(I)mechNutz = R · (IA - I) · (I - IL) .
Die elektrische Leistung ist Nel = U · I , wobei U durch R·IA ersetzt werden kann.
N(I)el = R · IA· I .
Der Wirkungsgrad ist η = NmechNutz / Nel :
(8a) η(I) = ( (IA - I) · (I - IL) ) / (IA· I) .
Maximum des Wirkungsgrads
d(η(I) /dI = (IL / I2) - (1 / IA), >>>> gleich Null gesetzt: I = (IL· IA) ½
Der Wirkungsgrad η ist maximal beim Strom-Wert I1 = (IL· IA) ½ .
η(I1) = ... [Zwischenrechnung übersprungen] ... = ( 1 - (IL/ IA) ½ ) 2
Der maximale Wert des Wirkungsgrads ist ηmax = ( 1 - (IL/ IA) ½ ) 2 .
Lage und Wert des Wirkungsgrad-Maximums hängen vom Parameter IL/ IA (Verhätnis zwischen Leerlauf- und Anfahr-Strom) ab.
Abb.8 enthält die Kurve für IL/ IA = 1/100, die der in Ab.2 sehr ähnlich aussieht. Auch der errechnete Maximalwert (81%) ähnelt dem angegebenen Wert ([2]: 82%).
Die Kurve in Abb.7 gilt für IL/ IA ≈ 1/13 (0,5A / 6,6A). Sie hat ihr Maximum bei ≈ 53% und ist "runder" als die Kurven für Motoren mit besserem Wirkungsgrad, die von beiden Seiten her bis nahe ans Maximum in guter Näherung linear sind.
![]() Siegfried Wetzel, CH 3400 Burgdorf, November 2015 (Dez.2015, Jan.2016)
Siegfried Wetzel, CH 3400 Burgdorf, November 2015 (Dez.2015, Jan.2016)