<< Home
<< andere Astronomie-Beiträge
↓↓  Ende

Ein altes Tellurium

Zusammenfassung

Ein von der Firma Utz AG in Bern in der Zeit um 1940 angefertigtes Tellurium wird untersucht. Seine Darstellungen der Bewegungen von Erde und Erd-Mond werden angegeben. Die verwirklichten Umlaufverhältnisse werden mit den tatsächlichen verglichen und Vorschläge gemacht, wie diese besser einander angeglichen werden könnten. Die Apsidendrehung des Mondes ist in diesem Modell fälschlicherweise relativ zur Sonne anstatt relativ zu den Fixsternen definiert. Für einen eventuellen Nachbau wird vorgeschlagen, wie sich diese Drehung korrekt und die Drehung der Knotenlinie zusätzlich verwirklichen ließe.

Inhalt

<< Abb.1 Ein altes Tellurium, um 1940

1. Ein erster Augenschein  ↑ Anfang

Die ersten Abbildungen (Abb. 1 und 2) zeigen, wie Modelle vor etwa 70 Jahren aussahen. Kunststoffe waren noch überwiegend unbekannt. Große Teile waren Grauguss-Stücke, die kleineren waren vorwiegend spanend bearbeitete Messing-Teile. Den Fuß als relativ schweres Guss-Teil auszuführen, hatte den Vorteil, dass das Tellurium trotz auskragender Erde-Mond-Gruppe nicht umkippte. Alle nötigen Getriebe wurden aus Zahnrädern gebildet, so wie es bei einem rein mechanischen, Uhren-ähnlichem Instrument in dieser Zeit üblich war.

<< Abb.2 Ein altes Tellurium, um 1940, Draufsicht

2. Die Technik eines Telluriums
  ↑ Anfang

Die relative Bewegung zwischen Erde und Sonne kann ohne fehlerhaft zu sein, sowohl geo- als auch heliozentrisch dargestellt werden. Bei der geozentrischen Methode hätte das Modell nur eine (1) Drehachse (gemeinsam für Sonne und Mond). Tellurien werden aber in der Regel heliozentrisch aufgestellt, wobei die Drehachse des Mondumlaufs zusammen mit der rotierenden Erde gegen die Sonne umläuft. Erschwerend ist, diese zusätzlich umlaufenden Drehungen anzutreiben.

Erleichtert wird die Stromzufuhr zur Glühbirne als Sonne. Mit deren Licht lassen sich Tag+Nacht auf der Erde, die Mondphasen und die Finsternisse andeutungsweise darstellen.

<< Abb.3 Tierkreis-Scheibe und Sonne (Glühbirne)

3. Die Technik des untersuchten
Telluriums  ↑ Anfang

Mit dem Guss-Fuß ist eine Glühbirne (vermutlich ursprünglich von einem kugeligen Lampenschirm umgeben), die die Sonne darstellt, und eine Scheibe mit aufgedrucktem Tierkreis, der den fixen Himmel (Fixsterne) repräsentiert, fest verbunden (Abb.3)

Unter der Tierkreis-Scheibe dreht sich der auf einer Hohlwelle befestigte Kragarm, der an seinem Ende das Erde-Mond-System trägt. Seine Drehung entspricht der jährlichen Bahnfahrt der Erde um die Sonne, die auf der festen Tierkreisscheibe von einem mitdrehenden Messing-Stift angezeigt wird. Die Erdachse ist 23,5° (Schiefe der Ekliptik) gegen die Bahn der Erde geneigt. Um sie dreht sich die Erde (ein Globus) einmal (1x) täglich.

Der Mond (graue Kugel) dreht sich um eine Achse, die durch den Erdmittelpunkt geht, aber senkrecht auf der Erdbahn steht. Ihre real etwa 5° betragende Kippung aus der Erdbahn heraus ist nicht nachgebildet. Der hin- und herschwenkende Tragarm des Mondes bewirkt dessen Abstandsänderung von der Erde infolge seiner elliptisch geformten Bahn.

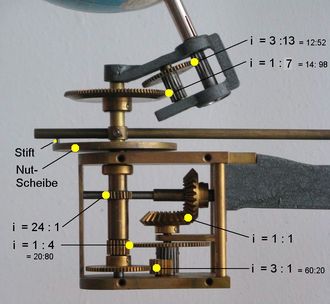<< Abb.4 Zahnrad-Getriebe am Ende des Kragarms

4. Die Antriebstechnik des untersuchten
Telluriums  ↑ Anfang

Mit der Handkurbel am Fuß wird über ein Schnecken-Getriebe der Kragarm feinfühlig gedreht (Jahres-Drehung). In seinem Inneren befindet sich eine lange Welle, die von einem Kegelrad-Getriebe unter der Tierkreis-Scheibe gedreht wird. Das mit ihr verbunden Kegelrad rollt auf einem am Fuß festen Kegelrad. Am ihrem anderen Ende (im Messing-Käfig, Abb.4) treibt diese Welle vier Drehbewegungen im Erde-Mond-System an.

4.a) Rück-Drehung der Erdachse:

Die Erdachse fährt um die Sonne, wobei sie parallel zu sich selbst bleibt. Eine solche Bewegung heißt Revolution (Abb.5). Dafür darf sie nicht starr auf dem Kragarm befestigt sein. Sie muss sich relativ zu ihm zusammen mit dem kleinen grauen Käfig, an dem sie befestigt ist, zurück drehen. Das wird durchs untere Stirnrad-Getriebe im Messing-Käfig erreicht. Es hat i₃ (=60:20=3:1), den Kehrwert der Kegelrad-Übersetzung i₁ (=16:48=1:3) für den Antrieb der langen Welle im Kragarm. Zur Umkehr der Drehrichtung enthält es ein kleines Zwischenrad. Das drüber befindliche Kegelrad-Getriebe hat die Übersetzung i₂=1:1.

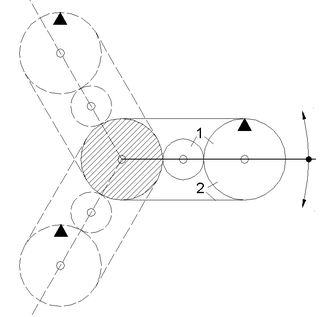<< Abb.5 Revolution des äußeren Rades ums fixierte zentrale Rad
schematisch, 1 - mit Wälzrädern, 2 - mit Band-Getriebe

4.b) Bahnfahrt des Mondes:

Die Umrundung der Erde durch den Mond dauert 29,53 Tage (Lunation). Diese Bahnfahrt ist gegenüber der Sonne gemessen, findet somit auch relativ zum Kragarm statt. Das zweite Stirnrad-Getriebe von unten im Messing-Käfig mit i₄ (=20:80=1:4) und eine erste (innere) Hohlwelle, die den Mond trägt, werden dazu gebraucht. Die Übersetzung bis hier beträgt i_M = i₁ × i₂ × i₄ = 1:3 × 1:1 × 1:4 = 1:12. Pro Jahr gibt es 12 Mond-Monate im Tellurium. Real sind es 12,37 Mond-Monate.

4.c) Apsiden-Drehung des Mondes

Die elliptische Mondbahn wird im Tellurium dadurch nachgebildet, dass der Mond während seiner Bahnfahrt hin- und hergeschwenkt wird. Die Schwenkung wird von einer exzentrischen Nut-Scheibe erzeugt. Ein in der Nut gleitender Stift bewegt sich horizontal. Seine Bewegung wird über eine im Tragrohr gleitende Stange auf den Schwenkarm übertragen. Die Nutscheibe wird mittels des Schnecken-Getriebes mit i₅ (=24:1) gedreht (Schneckenrad auf einer zweiten, äußeren Hohlwelle), was der Apsiden-Drehung der Mondbahn entsprechen soll. Leider hat das Tellurium hier einen prinzipiellen Fehler. Die Periode ist mit 8 Jahren für 1 Drehung (i_A = i₁ × i₅ = 1:3 × 24:1 = 8:1) zahlenmäßig annähernd richtig (Soll 8,85 Jahre). Die Drehung der Bahnellipse hat diesen Wert aber relativ zu den Fixsternen, nicht relativ zur Sonne bzw. relativ zum Kragarm. Die gleiche Relativität besteht übrigens bei der im Tellurium nicht nachgebildeten Drehung der Knotenlinie der Mondbahn.

4.d) Eigen-Drehung der Erde

Die Eigendrehung der Erde wird von der den Mond bewegenden zentralen Welle über zwei weitere Zahnrad-Getriebe erzeugt: i_E = i_M × i₆ × i₇ = 1:12 × 1:7 × 3:13 = 3:1092 = 1:364.
Im Tellurium gibt es 364 Tage. Real sind es 365,24 Tage.
i_L= i₆ × i₇ = 1:7 × 3:13 = 1:30,33
i_L zeigt die Dauer einer (1) Lunation mit 30,33 Tagen an, real sind es 29,53 Tage. Sowohl der Mond-Monat als auch der Tag sind eine (1) Runde bzw. eine (1) Drehung gegen die Sonne gemessen. Somit ist richtig, dass diese Bewegungen im Tellurium auf den Kragarm bezogen sind.

5. Genauere Übersetzungsverhältnisse  ↑ Anfang

Hiermit wird ein erster Vorschlag dafür unterbreitet, wie bei einem allfälligen Nachbau eine bessere zahlenmäßige Übereinstimmung zwischen den im Tellurium erzeugten und den tatsächlichen Bewegungen im Sonne-Erde-Mond-System möglich wäre. Die vorgeschlagenen Zähnezahlen sind allerdings nicht immer mit einem gebräuchlichen Teilapparat zu verwirklichen, eine modernere Mess-/Teil-Methode ist dafür erforderlich.

 i     bisher    Vorschlag     Soll
 ------------------------------------
 i1    16:48      16:49		
 i2    25:25      25:25
 i3    60:20      49:16
 i4    20:80      20:81
 iM    1:12       1:12,40     1:12,37
 i6    14:98      12:72
 i7    12:52      12:59	
 iE    1:364      1:365,89    1:365,24
 iL    1:30,33    1:29,50     1:29,53

6. Konstruktionsvorschlag für einen erweiterten Nachbau  ↑ Anfang

Bei einem bloßen Nachbau wäre der Verzicht auf die Apsiden-Drehung des Mondes ihrer prinzipiell falschen Lösung vorzuziehen. Diese Bewegung korrekt einzubauen, ist ein größerer Aufwand. Falls er geleistet wird, wäre die gleichzeitige Verwirklichung der Knoten-Drehung ins Auge zu fassen. Der folgende Konstruktionsvorschlag geht auf diese doppelte Erweiterung ein. Die komplette Lösung wird im Prinzip dargestellt. Die Prinzip-Zeichnung (Abb.6) enthält zwei Hauptbereiche:

a) die vier (4) ineinander steckenden Wellen und die von ihnen bewegten Teile
b) die drei (3) Antriebe für die Wellen

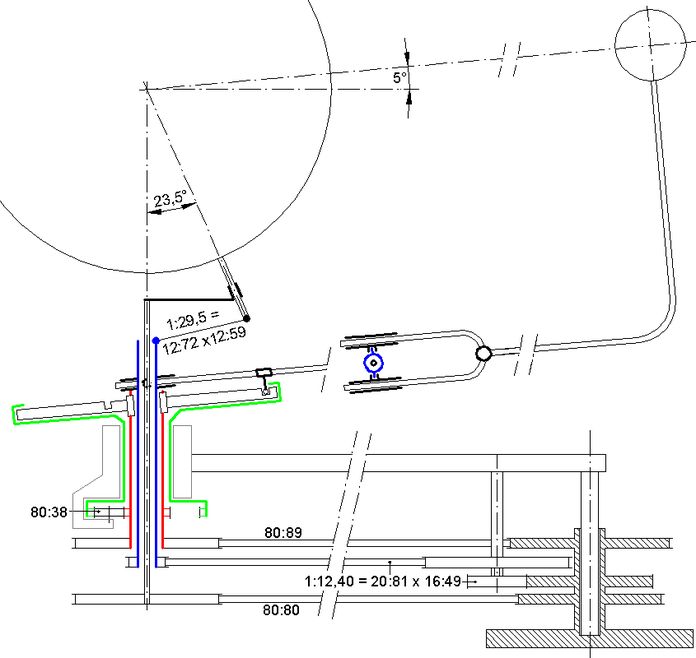Abb.6 Tellurium, Nachbau (links: 4 ineinander steckende Wellen; rechts: 3 Antriebe für die Wellen

6.a) Die vier ineinander steckenden Wellen

Die zentrale Welle mit der schräg aufgesetzten Erdachse ist jetzt von drei (anstatt bisher zwei) Hohlwellen umgeben, die alle Mondbewegungen antreiben, von innen nach außen:

1. seinen Umlauf (Lunation)
2. seine Apsidenlinie
3. seine Knotenlinie

An der 1. Hohlwelle fährt der Mond-Arm radial aus und ein, um die Abstandsänderung des Mondes von der Erde zu ermöglichen. Die Änderung wird durch das Spuren des Arm-Stiftes in der exzentrischen Nut der 5° geneigten Scheibe erzeugt. Die gegabelte Verbindung des Armes mit der Welle pendelt zudem um eine horizontale Achse, damit der Mond über die Knoten auf- und absteigen kann.

Die 2. Hohlwelle treibt wie bisher die Nut-Scheibe an (Apsiden-Drehung). Sie wird aber jetzt bezogen auf einen unendlich fernen Punkt einmal (1x) gedreht, während der Kragarm sich 8,89 mal (Soll 8,85 Jahre) dreht. Da sie um eine 5° von der Welle abweichende Achse dreht, ist sie mit ihr mittels eines Kugel-Gelenkes (Dreh-Kopplungsgrad k=1, Dreh-Freiheitsgrad f=2) verbunden.

Die 3. Hohlwelle dreht die geneigte Auflage der Nut-Scheibe. Deren Achse erhält dadurch eine Präzessions-Bewegung. Die Knoten-Linie der Mondbahn dreht sich bezogen auf einen unendlich fernen Punkt einmal (1x), während der Kragarm sich 18,72 mal (Soll 18,61 Jahre) dreht. Die Welle trägt unten ein Innen-Zahnrad als Bestandteil eines Getriebes zwischen 2. und 3. Hohlwelle. Zwischen den realen Dreh-Geschwindigkeiten der Knoten-Linie und der Apsiden-Linie ist das Verhältnis 18,61:8,85 = 2,103. Das vorgeschlagene Verhältnis ist 80:38 = 2,105.

Die Erd-Drehung wird wie bisher zusätzlich von der 1. Hohlwelle über die beiden Zahnrad-Triebe i₆ und i₇ (nicht gezeichnet, genauere Übersetzungsverhältnisse 12:72 und 12:59) erzeugt.

Der den Mond tragende Arm ist nochmals in Aufsicht im Bereich seines gegabelten Endes gezeichnet.

6 b) Die drei Antriebe für die Wellen

Es handelt sich um die Antriebe der zentralen Welle und der beiden ersten Hohlwellen. Der Kragarm könnte im Querschnitt ein U-Profil haben, in dessem Freiraum die drei (3) vorgeschlagenen Band-Triebe (Zahnriemen) Platz haben, die die bisherigen Zahnrad-Triebe i₁ bis i₅ ersetzen.

Der untere 1:1- Band-Trieb führt zur zentralen Welle, womit deren Revolution ermöglicht wird (s.Abb.5, 2). Dem mittleren Band-Trieb ist ein Zahnrad-Trieb vorgeschaltet, der außer einem Anteil am Übersetzungsverhältnis auch die Drehrichtungs-Umkehr übernimmt. Beide Übersetzungsverhältnisse haben die für i₁ und i₄ vorgeschlagenen verbesserten Werte (s.5.) zum Antrieb des Mondes.

Der obere Band-Trieb dreht die Apsiden-Linie. Von 89:80 (Kehrwert des Übersetzungsverhältnisses) ist 1 abzuziehen, weil sie sich relativ zu einem unendlich fernen Punkt (nicht zum Kragarm) dreht: 89:80 - 1 = 1,1125 - 1 = 0,1125 = 1:8,89 (Soll-Wert 1:8,85).

↑↑  Anfang
<< Druck-Version (4 Seiten, *.pdf, 320 KB)
<< Home
<< andere Astronomie-Beiträge

    Siegfried Wetzel, CH 3400 Burgdorf, November 2010 (Apr.2011)