<< Home
<< andere Astronomie-Beiträge
↓↓  Ende

Das Perihel der Erde

Zusammenfassung

Zuerst wird der Einfluss des wechselnden Kalenderdatums des Perihels der Erde auf die Zeitgleichung angesprochen. Insbesondere wird untersucht, wie die Zeitgleichung zu korrigieren ist, wenn man beachtet, dass sich das zweite Kepplersche Gesetz nicht auf die Bahnfahrt der Erde, sondern auf die ihres mit dem Erd-Mond gemeinsamen Baryzentrums bezieht.

Im folgenden größeren Teil der Arbeit werden die geometrischen Zusammenhänge bei der Entstehung der wechselnden Perihel-Zeitpunkte und der wechselnden kleinsten Abstände der Erde von der Sonne behandelt.

Inhalt

1. Einleitung  ↑ Anfang

Das Datum des Perihels wird bei der Berechnung der Zeitgleichung benötigt, sowohl bei deren angenäherter als bei deren strengerer Berechnung. In beiden Fällen wird nicht das Datum des kleinsten Abstandes der Erde von der Sonne sondern das Datum des Durchgangs ihres mit dem Erdmond gemeinsamen Schwerpunktes - des Baryzentrums - durch die Apsidenlinie verwendet. Dass bei diesem Vorgehen der gemachte Fehler vernachlässigbar klein ist, wird im Folgenden nachgewiesen.

Andererseits werden die massstäblich nicht darstellbaren geometrischen Relationen zwischen Sonne, Erde und Mond beim bis mehr als einem Tag ausmachendem Vor- bzw. Nachlauf des Datums für den kleinsten Sonnenabstand der Erde (das Perihel der Erde) prinzipiell erfasst und erklärt. Dabei werden auch quantitativ annähernd richtige Antworten gegeben. Als ordnender Paramater für die verschieden Fälle erweist sich die Phase des Mondes im Moment des Apsidendurchgangs des Baryzentrums oder im Moment des Perihels der Erde.

2. Perihel und Zeitgleichung  ↑ Anfang

Dass die Erde im Perihel den kleinsten Abstand zur Sonne hat, spielt bei der Zeitgleichung keine direkte Rolle. Bei deren Behandlung wird lediglich der Zeitpunkt des Periheldurchgangs der Erde (genauer: seines des Erde-Mond-Baryzentrums) als Bezugspunkt auf der Zeitachse gewählt. Denn in der Astronomie ist es allgemein üblich, den Zeitpunkt, zu dem die Position eines Planeten zu bestimmen ist, mit der Differenz zum Zeipunkt seines Periheldurchgangs anzugeben. Interessieren kann aber der mit den Mondphasen periodisch variierende, auf der Erdbahn gemessene Abstand zwischen Erdschwerpunkt und Barryzentrum, denn die Lage Letzteren wird in in der Zeitgleichung mit der Kepler-Gleichung verrechnet. Diese Schwankung tritt andauernd auf, nicht nur, wenn das Perihel passiert wird. Die zu klärende Frage stellte sich mir also nur zufällig im Zusammenhang mit meiner Perihel-Beschäftigung. Sie lag aber längst in der Luft: Bei meinen bisherigen Arbeiten über die Zeitgleichung habe ich sie mit gleicher Intensität verdrängt, mit der sie in der einschlägigen Literatur nicht auftaucht.

Im Kalender hat auch der Zeitpunkt für den Durchgang des Baryzentrums durch die Apsidenlinie kein festes Datum. Das ergibt sich daraus, dass der jährliche Erdumlauf nicht mit ganzen Kalendertagen angegeben werden kann. In meiner angenäherten Behandlung der Zeitgleichung ist die Festlegung auf den 3. Januar, 12 Uhr UTC nur eine weitere unter den sonst enthaltenen Näherungen. In meiner strengeren Behandlung wird die Schwankung über etwa 3 Januar-Tage mit der sogenannten Jahreskonstanten M₀, die sich im Wesentlichen im Rhythmus der Schaltjahre ändert, berücksichtigt.

Der etwa 4700 km Abstand zwischen Erdschwerpunkt und Barryzentrum wird bei zu- und bei abnehmendem Mond in ganzer Größe auf der Erdbahn abgebildet (s. Abb.3, rechts). Die auf ihrer Bahn etwa 30 km/sec schnelle Erde läuft dem Baryzentrum etwa 2 ¾ min voraus bzw. nach. Falls sich diese fast ± 3 min direkt auf die Zeitgleichung auswirken würden, wären alle berechneten und gebrauchten Zeitgleichungs-Werte erheblich falsch. Sie wirken sich tatsächlich nur mir knapp ± 0,5 sec aus, was folgende Überlegung zeigt:

3. Das Perihel der Erde - ihr kleinster Abstand von der Sonne  ↑ Anfang

3.1 Vorgehensweise  ↑ Anfang

Vom Jet Propulsion Labrotory (JPL) des California Institute of Technology gibt es einen on-line Rechen-Dienst (HORIZONS Web-Interface) für die Ermittlung von Ephemeriden im Sonnensystem. Damit ist es unter vielem anderen möglich, die auf die Sonne (Sun) bezogenen Ephemeriden sowohl für die Erde (Geocenter) und für den Mond (Luna), als auch für deren gemeinsames Baryzentrum (EMB) für auf die Minute vorgebbare Zeitpunkte zu berechnen.

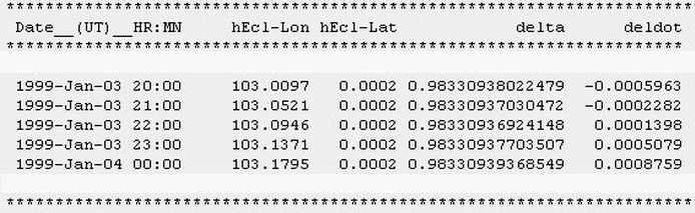Abb.1 oben: Startseite des HORIZONS Web-Interface (Ausschnitt)
          mit für die Epheremiden-Rechnung für das Erde-Mond-Baryzentrums (EMB) nötigen Einstellungen,
          gültige Werte beim deldot-Wechsel von - auf +
          nach 1. Annäherung Zeitbereich (Time Span) einschränken und Schrittgröße (Step) auf Minute (1 m) verkleinern
          unten: Ergebnis-Ausdruck (Ausschnitt)

Es werden alle Perihel-Situationen zwischen den Jahren 1989 und 2020 (32 Fälle) untersucht. In den Diagrammen in Abb.2 sind für jedes Jahr

1. der Abstand zwischen den Zeitpunkten der Baryzentrum-Lage auf der Apsidenlinie der Erdbahn-Ellipse und
    des Perihels der Erde und
2. das verschiedene Mass der Annäherung der Erde an die Sonne eingetragen.

Auf den Abszissen ist die Mondphase als Winkel eingetragen (Vollmonde: 0°, Neumonde: ±180°). Einzelheiten zur Untersuchung im Anhang 1.

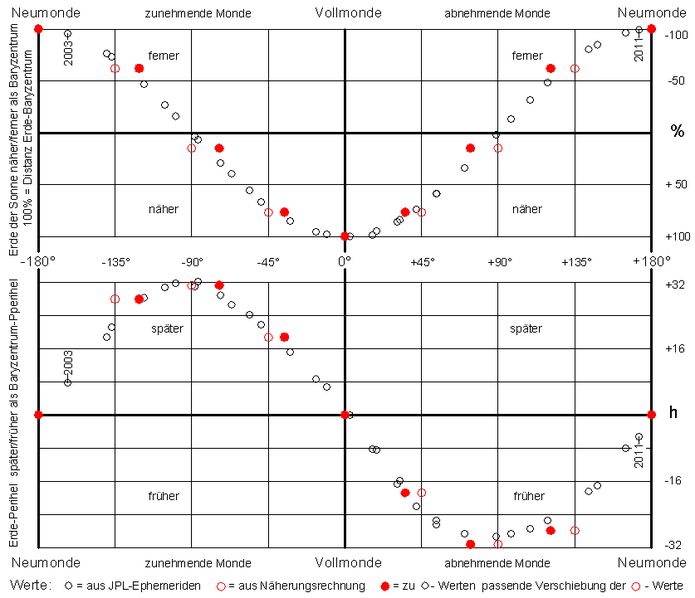Abb.2 Unterschiedliche Sonnennähe (oben) und
          unterschiedlicher zeitlicher Abstand des Erde-Perihels vom Baryzentrum-Perihel (unten)
          in Abhängigkeit von der Mondphase (Winkel -180° bis +180°) zur Zeit des Perihels

Die Verläufe der von den Digramm-Punkten o gebildeten Kurven werden in den folgenden Abschnitten (3.2 bis 3.5) mit Hilfe prinzipieller geometrischer Überlegungen und Rechnungen näherungsweise gedeutet. Die Rechengenauigkeit ist eingeschränkt, weil die verwendeten Konstanten nur Durchschnittswerte sind. Der Monumlauf wird gleichmässig auf kreisförmiger Bahn angenommen. Für jeden der behandelten Fälle gilt aber z.B. eine andere Mondperiode (siderischer Monat) und eine andere Entfernung des Mondes von der Erde (Mondbahnellipse mit relativ großer Exzentrizität, wodurch die Distanz zwischen Geozentrum und Baryzentrum variiert). Dass die Mondbahnebene nicht mit der Erdbahnebene zusammenfällt (gegenseitige Inklination etwa 5°), wird nicht beachtet. Die Näherung der Erdbahn im Ellipsen-Hauptscheitel mit dem Scheitelkreis (SchK) ist vergleichsweise genauer, ebenfalls das Rechnen mit der durchschnittlichen Umlauf- Geschwindigkeit der Erde.

3.2 Das Perihel der Erde bei Halbmond  ↑ Anfang

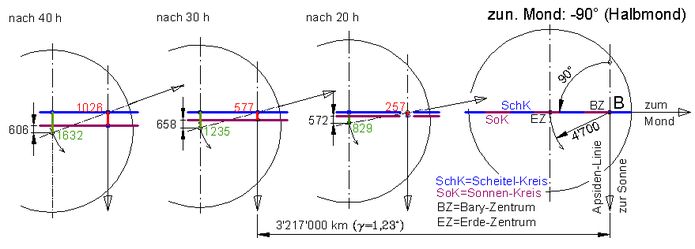Abb.3 Erde und zunehmender, genau halber Mond passieren von rechts nach links den Scheitel B der Bahnellipse.
          Distanzen zw. Drehlagen des Erde-Mond-Paares zu verschieden Zeitpunkten etwa 200 mal verkleinert (geringe
          kleine Drehung um γ - s. Abb.6 - gegenüber der Apsidenlinie nicht gezeichnet).
          Maßzahlen (aus Abb.5) ohne Einheiten: km

Bei genau halbem Mond liegen die drei Punkte (Baryzentrum und Schwerpunkte von Erde und Mond) ziemlich genau auf der elliptischen Bahn, weil diese über die nur etwa 380'000 km Entfernung zwischen Erde und Mond fast als Gerade angesehen werden kann. In Abb.3, rechts befinden sich Erdeschwerpunkt (≈ Erdezentrum) und Barryzentrum bei zunehmendem Halbmond auf dem als Gerade erscheinenden Bahnstück; der nicht gezeichnete Mond liegt nur unwesentlich außerhalb der Bahnellipse.

Im Folgenden wird gezeigt, dass die Erde bei genau halbem Mond (symmetrische Verhätnisse bei zu- und abnehmenden Mond) nicht zum Zeitpunkt ihres Scheiteldurchgangs (genauer: des Scheiteldurchgangs des Baryzentrums) der Sonne am nächsten ist. Sie ist es bei zu- bzw. abnehmendem Mond mehr als 30 Stunden später bzw. früher.

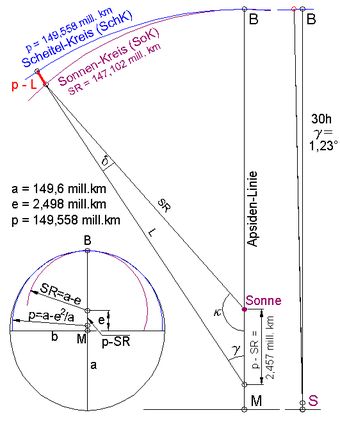<< Abb.4 Sonne und elliptische Erdbahn
               rechts: masstäbl.(γ=1,23°); links: schematisch
               links unten: ganze Bahn, verkleinert

In Abb.4 sind die Verhältnisse etwa 10'000 mal kleiner als in Abb.3 dargestellt, um die Sonne mit ins Bild zu nehmen. Die Darstellung am rechten Bildrand ist massstäblich. Erde mit Mond und Sonne lassen sich nur als Punkte angeben, und der interessierende keilförmige Spalt zwischen dem Scheitelkreis (ausreichende Näherung an die Ellipse im Scheitel B) und dem sogenannten Sonnenkreis ist nicht erkennbar. Deshalb wird die schematische Darstellung links daneben mit etwa 15 fach vergrößerter Exzentrizität (ε = 0,25 anstatt ε = 0,0167) benutzt. Das in der massstäblichen Darstellung nicht erkennbare, zur Berechnung erforderliche Dreieck (γ - β - κ) wird auf diese Weise "aufgeklappt".

Sofort nach Verlassen des Punktes B (momentaner Ort des Baryzentrums) wird das Erdezentrum zur Sonne hin gedreht, und die Erde kommt näher an die Sonne heran (Mond bewegt sich nach außen). Die Näherung setzt sich solange fort, bis der Gewinn durch die Revolution genannte Drehung von der Abstandvergrößerung zum sogenannten Sonnenkreis übertroffen wird. Der Gewinn durch Revolution verkleinert sich progressiv und ist beim Erreichen des Neumondes (nach etwa 177 Stunden) Null. Der Verlust durch das ebenfalls progressive Aufgehen der Schere zwischen Erdbahn (Scheitelkreis) und Sonnenkreis (Vergrößerung der "Längen-Differenz") bewirkt, dass die maximale Näherung an die Sonne aber schon nach etwa 30 Stunden (1¼ Tag) erreicht ist (s.Abb.3: 663 km ≈1241-577 näher als Scheitelpunkt B).

Die folgende Tabelle (Abb.5) enthält die Rechenergebnisse für in engeren Abständen als zwischen in Abb.3 einander folgenden Zeitpunkten. Demnach erreicht die Erde ihre größte Sonnennähe 31¼ Stunden später als nach zunehmenden genauem Halbmond, der stattfindet, wenn das Baryzentrum die Apsidenlinie passiert. Sie ist der Sonne 659 km (14,9% der Distanz Erde-Baryzentrum) näher als das Baryzentrum. Einzelheiten zur Berechnung im Anhang 2.

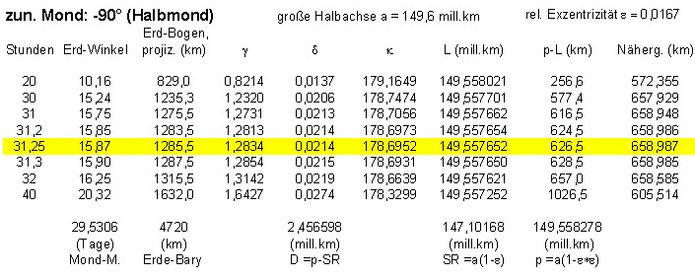Abb.5 Ergebnisse für die Berechnung der besten Sonnennähe bei Halbmond (zunehmend):
          maximale "Näherung" 31¼ Stunden später als genauer Halbmond;
          vorgegebene Größen oben und teilweise zusammen mit daraus abgeleiteten Größen unter den
          Zwischenergebnis-Spalten (Ergebnisse in den Spalten mit den darunter stehenden Größen ermittelt)
          Winkel-Werte in ° (Alt-Grad)

3.3 Das Perihel der Erde bei Viertel- bzw. Dreiviertelmond  ↑ Anfang

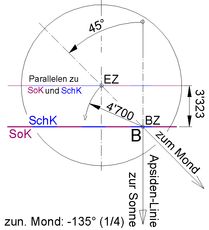
<<<< Abb.6 Viertelmond (zunehmend) bzw.
    << Abb.7 Dreiviertelmond (zunehmend)
         Zeitpkt.: Baryzentrum auf Apsidenlinie

Das Erde-Zentrum befindet sich im Anfangs-Moment nicht auf der Bahnellipse, sondern auf einer Parallele dazu. Die Überlegungen und Rechnungen unterscheiden sich gegenüber Abschnitt 3.2 (Halbmond) lediglich darin, dass von je einem Parallelkreis p' zum Scheitel- bzw. von je einem Parallelkreis SR' zum Sonnenkreis auszugehen ist: Parallelkreise größer/kleiner bei Viertel-/Dreiviertelmond (Größen von p' und SR': s. Abb.n 8 und 9). Bei der Berechnung des "Erd-Bogens, projiz." ist die andere anfängliche Winkellage der Geraden Erde-Baryzentrum-Mond zu beachten.

Abb.8 Ergebnisse für die Berechnung der besten Sonnennähe bei Viertelmond:
          maximale "Näherung" etwa 28 Stunden nach genauem Viertel-Mond:
          2908 km (3323-415) weniger nahe als das Baryzentrum (61,9% der Distanz Erde-Baryzentrum)

Abb.9 Ergebnisse für die Berechnung der besten Sonnennähe bei Dreiviertelmond:
          maximale "Näherung" etwa 18¾ Stunden nach genauem Dreiviertel-Mond
          3602 km (3323+279) näher als das Baryzentrum (76,6% der Distanz Erde-Baryzentrum)

3.4 Das Perihel der Erde bei Neumond  ↑ Anfang

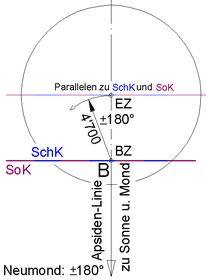<< Abb.10 Erde und genauer Neumond passieren von rechts nach links
                 den Scheitel B der Bahnellipse.

Bei genauem Neumond zum Zeitpunkt des Scheiteldurchgangs hat die Erde generell die schlechteste "Perihel-Nähe" zur Sonne. Fraglich ist, ob sie zu einem späteren (oder früheren) Zeitpunkt der Sonne näher ist. Da sich die Erde sowohl um das Baryzentrum als auch um die Sonne mit Null-Gradient aus der B-Lage heraus bewegt, kann die Antwort ohne Rechnung nicht gegeben werden. Beim Rechnen treten zudem Subtraktionen zwischen Zahlen auf, die sich voneinander erst nach etwa 8 Stellen unterscheiden.

Die Überlegungen und Rechnungen unterscheiden sich gegenüber Abschnitt 3.2 (Halbmond) lediglich darin, dass von einem Parallelkreis p' zum Scheitel- bzw. von einem Parallelkreis SR' zum Sonnenkreis auszugehen ist: Parallelkreise um Erde-Bary-Distanz größer (Größen: s. Abb.11). Bei der Berechnung des "Erd-Bogens, projiz." ist die andere anfängliche Winkellage der Geraden Erde-Baryzentrum-Mond zu beachten.

Die folgende Tabelle (Abb.11) enthält die Ergebnisse. Der Erdmittelpunkt entfernt sich später (und früher) weiter von der Sonne (negative Werte in der Spalte "Näherung") als im Zeitpunkt des genauen Neumondes (0 Stunden).

Abb.11 Ergebnisse für die Berechnung der besten Sonnennähe bei Neumond:
            keine weitere "Näherung" gegenüber genauem Neumond.

3.5 Das Perihel der Erde bei Vollmond  ↑ Anfang

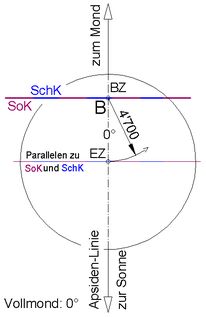<< Abb.12 Erde und genauer Vollmond passieren von rechts nach links
                den Scheitel B der Bahnellipse.

Bei genauem Vollmond zum Zeitpunkt des Scheiteldurchgangs befindet sich die Erde generell am nächsten bei der Sonne. Sie dreht sich sowohl um das Baryzentrum als auch um die Sonne mit Null-Gradient aus der B-Lage heraus (oder hinein). Weil aber beide Drehpunkte auf verschiedenen Seiten des Erdeschwerpunktes liegen, wird diese beste Sonnennähe später (oder früher) als zum Zeitpunkt, wenn das Baryzentrum bei genauem Vollmond die Apsidenlinie passiert, nicht überboten.

3.6 Diskussion der Ergebnisse  ↑ Anfang

Die in den Abschnitten 3.2 bis 3.5 näherungsweise errechneten Werte sind in die Diagramme der Abb.2 als rote Punkte eingetragen. Die Rechnungen selbst hatten das Bary-Perihel als zeitlichen Nullpunkt und führten zu den mit kleinen roten Kreisen gekennzeichneten Werten. Da die JPL-Ephemeriden für die Zeitpunkte (und die Mondwinkel, Skalen von -180° bis +180°) des Erde-Perihels ermittelt waren, wurden die roten Kreise den errechneten Unterschieden gegen das Bary-Perihel entsprechend verschoben (z.B Halbmonde: ±31¼ Stunden » ±15,9°).

Anfänglich wurden die JPL-Werte "Näherung" (Abb.2, oben) in Prozenten der mit 4'700 km konstant angenommen Distanz zwischen dem Geo- und dem Baryzentrum ermittelt. Weil sich dabei fragliche Werte ( u.a. >100%) ergaben, musste die Rechnung verfeinert werden. Nach verschiedenen Versuchen wurde diese Distanz schließlich zum Zeitpunkt des Erde-Perihels jeden einzelnen Falls ermittelt. Dazu wurden die von JPL auch angegebenen ekliptikalen Längenwinkel von Erdzentrum und Mond und das Masseverhältnis Erde zu Mond mit 81,3 benutzt. In den untersuchten Fällen schwankt diese Distanz zwischen 4'353 und 4'922 km, also um mehr als ±6% um den Mittelwert 4'638 km. Der Arbeitsaufwand hatte sich wesentlich über das anfänglich vorgestellte Mass hinaus erhöht.

Die Überlegungen und Näherungsrechnungen bestätigen grundsätzlich und mit sogar relativ hoher Genauigkeit die Abhängigkeiten der

1. Differenz zwischen den Zeitpunkten des Baryzentrum-Perihels und des Erde-Perihels und
2. des Masses der Näherung der Erde an die Sonne

von der Mondphase in der Zeit des Perihels des Erde-Mondsystems.

Die geringen Abweichungen der roten Punkte von den von den schwarzen Kreisen gebildeten Kurven in Abb.2 scheinen neben zufälligen auch systematische Gründe zu haben, die mit nochmals erhöhtem Aufwand vermutlich erkannt werden können.

4. Anhänge   ↑ Anfang

Die folgende Excel-Tabelle (Abb.13) enthält die JPL-Ephemeriden und die daraus errechneten Größen, die in den Diagrammen der Abb 3 dargestellt sind.

Spalte 1: Jahr (32 Fälle 1989 bis 2020)

Spalten 2 und 3: Datum und Uhrzeit (UT) für Baryzentrums- und Erdzentrums-Perihel. Schrittweise Annäherung zuerst mit Stunden-Intervall vom 1. bis 5. Januar, dann mit Minuten-Intervall in der vorher gefundenen Stunde.

Spalte 4: Zeitdifferenz zwischen Baryzentrums- und Erdzentrums-Perihel. Zeilen dem entsprechend geordnet: zwischen früherem (-Differenz) und späterem (+Differenz) Erde-Perihel. Die Zeitdifferenzen sind in Abb.3, unten eingetragen.

Spalten 5 und 6: Entfernungen (delta) des Erd- und des Bary-Zentrums von der Sonne (Zeitpunkt: Erde-Perihel)

Spalte 7: Differenz der Werte in den Spalten 5 und 6. Sie zeigt, wieviel das Erdzentrum der Sonne näher (+Differenz) oder ferner (-Differenz) als das Baryzentrum ist. Für Rechnung in Spalte 12.

Spalte 8: Entfernung (delta) des Mond-Zentrums von der Sonne. Für Rechnung in Spalte 11.

Spalten 9 und 10: Sonnenzentrische ekliptikale Längenwinkel (hEcl-Lon) des Erd- und des Bary-Zentrums. Für Rechnung in Spalte 11.

Spalte 11: Distanz zwischen Erd- und Baryzentrum. Die Rechnung erfolgte nicht direkt im Dreieck Erdzentrum-Sonne-Baryzentrum sondern im weniger spitzen Dreieck Erdzentrum-Sonne-Mond, weil die ekliptikalen Winkel nur mit 4 Nachkommastellen zur Verfügung standen. Die errechnete Distanz Erdzentrum-Mond wurde durch 82,3 dividiert (Massenverhältnis Erde/Mond = 81,3). Der ursprünglich mit 4'700 km konstant angenommene Wert wurde durch diesen in jedem Fall leicht anderen Wert (Zeitpunkt: Erde-Perihel) ersetzt. Für Rechnung in Spalte 12.

Spalte 12: Wert aus den Spalte 7 auf Wert aus Spalte 11 bezogen (%). Die prozentualen Werte sind in Abb.3, oben eingetragen.

Spalte 13: Richtung der Verbindungsline Erdzentrum-Baryzentrum, errechnet im bei Spalte 11 beschriebenen Dreieck. Bezugsgerade ist die Gegenrichtung zur Sonne (0° für Vollmonde, <0° für zunehmende Monde, >0° für abnehmende Monde) Die in Abb.3 enthaltenen Größen (Ordinatenwerte) sind als Funktion dieses Winkels (Abszissenwerte) dargestellt.

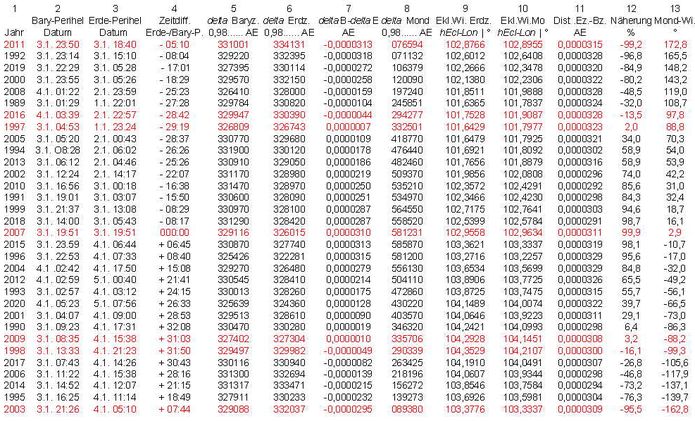Abb.13  zu Abschnitt 3.1: Excel-Tabelle mit Ephemeriden und deren Untersuchung (32 Fälle)    ↑ zurück

Die geringen Schwankungen der großen Halbachse und der Exzentrizität der Erdbahn müssen bei genauen Perihel-Berechnungen berücksichtigt werden. Bei den vorliegenden Berechnungen werden langfristige Mittelwerte verwendet (s. Kopfzeile in den Tabellen).

Die Distanz zwischen Erde-Schwerpunkt und Baryzentrum "Erde-Bary" ändert sich von Mond- zu Mond-Periode. Bei den vorliegenden prinzipielen Überlegungen und Rechnungen wird "Erde-Bary" = 4'700km gesetzt.

Für die Berechnung der kleinen Winkel "Erde-Winkel" und γ werden die Bahn-Umläufe des Mondes und der Erde mit Kreisen genähert angenommen. Die Umlaufzeiten sind 29,5306 (siderischer Mond, da auf die Sonne bezogen) bzw. 365,25 Tage.

Gleichungen für Abschnitt 3.2 (für andere Mondphasen sind einige Gleichungen zu variieren):

"Erde-Winkel" = "Stunden"h · 360° / (29,5306·24h)
"Erd-Bogen, projiz." = "Erde-Bary" · sin("Erde-Winkel")
 γ = "Stunden"h · 360° / (365,25·24h
 δ = arcsinγ · (p-SR) / SR
 κ = 180° - γ - δ
L= SR · sinκ / sinγ
"Näherg." = "Erd-Bogen, projiz." - (p-L)    ↑ zurück

Siegfried Wetzel, CH 3400 Burgdorf, Juli 2014

↑↑  Anfang << Home
<< andere Astronomie-Beiträge