|
<< Home GezeitenkräfteInhalt1. Einleitung2. Erklärungen und Berechnungen 2.1 Zwei Himmelskörper umrunden sich gegenseitig 2.2 Die Gezeitenkraft des Mondes 2.3 Die Gezeitenbeschleunigung des Mondes 2.4 Werte der vom Mond verursachten Gezeitenbeschleunigung auf der Erde 2.5 Erklärung der Gezeitenkräfte für einen auf der Erde ruhenden Beobachter 2.6 Werte der von der Sonne verursachten Gezeitenbeschleunigung auf der Erde 3. Anmerkungen 1. Einleitung ↑ Anfang
Die als Ebbe und Flut bekannten Gezeiten sind eine Folge von vorwiegend zwischen Mond und Erde wirkenden Anziehungskräften (Gravitationskräften). Solche Kräfte wirken grundsätzlich zwischen allen Himmelskörpern, wobei sie umso stärker sind, je enger die Nachbarschaft zwischen den Körpern ist. In Anlehnung an das irdische Gezeitenphänomen nennt man sie Gezeitenkräfte. Dass sie zu Ebbe und Flut führen, gilt aber nur auf der Erde, die als einziger Himmelskörper Wasser - insbesondere in Massen in ihren Ozeanen - besitzt. Die anderen Himmelskörper werden nur - wie der feste Erdkörper zusätzlich zu den Gezeiten auch - durch Gezeitenkräfte elastisch und z.T. bleibend verformt. 2. Erklärungen und Berechnungen ↑ Anfang2.1 Zwei Himmelskörper umrunden sich gegenseitig ↑ AnfangDie Anziehungskraft zwischen den Himmelskörpern bewirkt, dass sich diese einander umrunden. Da sie frei beweglich sind, werden sie nach dem Grundgesetz der Mechanik (erstes NEWTONsches Axiom) durch diese Kraft beschleunigt. Als beschleunigte Bewegung ist je eine stabile elliptische Umlaufbewegung entstanden, denn bei geradlinig beschleunigter Bewegung hätten sie sich vereinigt und würden individuell nicht mehr existieren.
In Abb.1 ist eine solche gegenseitige Umrundung schematisch dargestellt. Die Bahnzentren der beiden Körper sind ihr gemeinsamer Schwerpunkt (Barryzentrum). Gezeigt sind Kreisbahnen, wie sie bei den meisten Himmelskörpern näherungsweise anstatt ausgeprägter Ellipsen vorkommen. Das Barryzentrum befindet sich auf der Verbindungsgeraden der beiden Körperschwerpunkte, wobei es auch innerhalb eines der beiden Körper liegen kann. Letzteres ist bei der Paarung Erde|Mond der Fall, denn die Erdmasse ist etwa achtzig mal größer als die des Mondes.
Die Anziehungskraft FG zwischen den Körpern der Masse m1 und m2 wird mit dem prinzipiell schon von NEWTON in den 1680er Jahren gefundenen Gravitationsgesetz bestimmt. Es lautet heute: 2.2 Die Gezeitenkraft des Mondes ↑ Anfang
Die Gravitationskraft (Anziehungskraft) ist nicht an allen Stellen der beteiligten Körper gleich. Die örtliche Ungleichheit ist die Ursache der Gezeiten und ist umso ausgeprägter je kleiner der Abstand zwischen den Körpern wie z.B. bei zentralen Himmelskörpern mit Planeten oder Monden ist. Hier haben die Gezeiten nicht vernachlässigbare Auswirkungen sowohl auf den Zentralkörper als auch auf seine Satelliten. 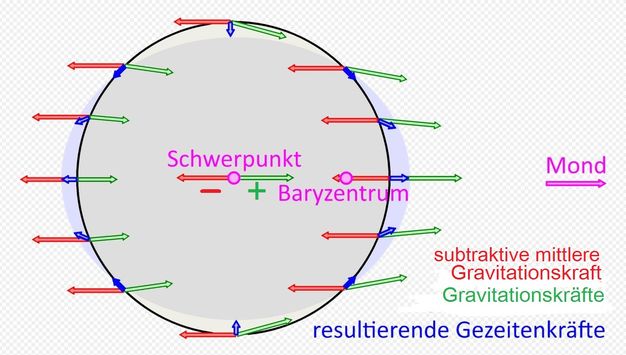 ←
Abb.2 Anziehungskräfte (Gravitationskräfte) des
←
Abb.2 Anziehungskräfte (Gravitationskräfte) des Mondes an der Oberfläche und im Inneren der Erde (im Schwerpunkt als Mittelwert) und resultierende Gezeitenkräfte In Abb.2 sind an mehreren Stellen der Erde die unterschiedlich großen Anziehungskräfte, die vom rechts befindlichen Mond ausgehen, als grüne Pfeile dargestellt. Die blauen Pfeile zeigen die Differenz zwischen der je an der Oberfläche und der mittleren im Erdinneren wirkenden Anziehungskraft (als mittlere gilt die im Erdmittelpunkt wirkendende). Die Kraftdifferenzen (nicht die gegenseitig verrechneten Kräfte), werden als Gezeitenkräfte bezeichnet (Anmerkung 1). Die Drehung der Erde um sich selbst bleibt unbeachtet, denn welche Orte mit bestimmten geographischen Koordinaten auf der Erde zu welchen Zeitpunkten betroffen sind, ist für die Vorarbeit, erst einmal die Gezeitenkräfte zu ermitteln, nicht relevant. An der dem Mond zugewendeten Seite ist die Anziehungskraft etwas größer als im Erdmittelpunkt. Die einigermaßen starre Erdkruste gibt diesem Kräfteunterschied kaum nach (Anmerkung 2). Sie verhält sich faktisch so, als wirke in ihr die gleiche Anziehungskraft wie im Erdmittelpunkt. Das frei bewegliche Wasser der Ozeane folgt der stärkeren Mondanziehung aber. Es bewegt sich zum Mond hin und bildet einen Flutberg. An der entgegengesetzten Seite der Erde verhält es sich gerade umgekehrt. Dort ist die Mondanziehung etwas geringer als im Erdmittelpunkt, was sich aber nur auf das Wasser der Ozeane auswirkt. Es bewegt sich vom Mond, aber auch von der Erde weg und bildet hier ebenfalls einen Flutberg. 2.3 Die Gezeitenbeschleunigung des Mondes ↑ AnfangDie Bearbeitung wird anstatt wie bisher mit Kräften F im Folgenden mit Beschleunigungen a fortgesetzt. Die Beschleunigung ist formal die Normierung der Kraft auf die Masse, die beschleunigt wird.a = F / m ist als entsprechende formale Darstellung eine Umstellung des NEWTON'schen Grundgesetzes für die beschleunigte Bewegung, dessen übliche Schreibweise F = m ·a (Kraft gleich Masse mal Beschleunigung) ist. Die Gravitationsbeschleunigung ist aG = G·M / r2 (anstatt r0 wie oben steht hier r, da auch Stellen außerhalb des Erdmittelpunktes betroffen sind). Sie anstatt der Gravitationskraft FG = G·m1·m2 / r2 zu verwenden, hat den Schreib-Vorteil, dass ein um eine Größe (m1 herausgekürzt (m2 wurde zu M=Mondmasse)) kürzerer Ausdruck vorliegt, und den arbeitstechnischen Vorteil, dass noch keine Festlegung auf die zu beschleunigende Masse (m1 >> m, die Erde als Ganzes oder Teile von ihr) besteht. Typischerweise werden die Differenzen ΔaG der Gravitationsbeschleunigung an den beiden mittleren Randpunkten der Erde zur Gravitationsbeschleunigung im Erdmittelpunkt gesucht. Der Abstand dieser Punkte vom Mondmittelpunkt ist r = r0 ± R (R=Erdradius). Die Beschleunigungsdifferenzen heißen analog zu den entsprechenden Kraftdifferenzen Gezeitenbeschleunigungen. ΔaG = a{r0±R} − a{r0} = G·M / (r0 ± R)2 − G·M / r02 Durch Umformen und Anwendung einer Näherung (siehe hier unter 3.1.1.1 Herleitung) erhält man ΔaG ≈ ∓ 2·R·G·M / r03 In dieser Schreibweise gilt die Gleichung nur für die beiden mittleren Randpunkte der Erde (größte Mondnähe bzw. -ferne). Sie lässt sich ohne Weiteres allgemein als für jeden beliebigen Oberflächenpunkt gültige Vektorgleichung formulieren. In der Abb.2 ist diese Allgemeingültigkeit für eine größere Zahl von Oberflächenpunkten in Form von Vektoradditionen graphisch dargestellt. 2.4 Werte der vom Mond verursachten Gezeitenbeschleunigung auf der Erde ↑ AnfangMit den Werten für R, G, M und r0R = 6,371·106 m, mittlerer Radius der Erde, G = 6,674·10−11 m3kg−1s−2, Gravitationskonstante (s.o.), M = 7,349·1022 kg, Masse des Mondes und r0 = 3,844·108 m, mittlere Entfernung des Mondes von der Erde ergeben sich für die Gezeitenbeschleunigung an den mittleren Randpunkten die Werte ΔaG ≈ ∓ 1,100·10−6 m/s2 (Gravitationsbeschleunigung im Erdmittelpunkt: aG0 = G·M / r02 = 3,319·10-5 m/s2) Weil r (=r0±R) quadratisch in die Rechnung eingeht, sind die beiden Randwerte absolut nicht gleich groß. Bei Verzicht auf die oben erwähnte Näherung bei der Herleitung der Gleichung für ΔaG wird das auch rechnerisch deutlich. Die Gleichung lautet dann ΔaG = G·M·( (1 / (1 ± R / r0)2 ) - 1 ) / r02 (siehe hier unter 3.1.1.1 Herleitung), und die Rechnung ergibt die beiden in absoluter Höhe nicht ganz gleichen Werte: ΔaG1 = − 1,074·10−6 m/s2 (mondabgewendete Seite), ΔaG2 = + 1,128·10−6 m/s2 (mondzugewendete Seite). Vergleiche: Die absoluten Werte von ΔaG1 und ΔaG2 weichen etwa ±2,5% vom Mittelwert ΔaG ab. Die Gravitationsbeschleunigung im Erdmittelpunkt ist etwa das 30-fache der Gezeitenbeschleunigungen (Anmerkung 1 und Anmerkung 3). Die an der Erdoberfläche von ihr selbst erzeugte Gravitationsbeschleunigung (Erdbeschleunigung) g = 9,81 m/s2 ist etwa zehnmillionenmal größer als die Gezeitenbeschleunigungen, weshalb Letztrere den Meeresspiegel auch nur um wenige Dezimeter anheben können. 2.5 Erklärung der Gezeitenkräfte für einen auf der Erde ruhenden Beobachter ↑ Anfang
Ruhendes und beschleunigtes Bezugssystem:
örtliche Zusammenfügen (Addieren) von Zentrifugalkräften und Gravitationskräften (Abb.3, rechts) ist der prinzipiell gleiche Vorgang wie das bisher vorgenommene Subtrahieren einer mittleren Gravitationskraft von örtlichen Gravitationskräften (Abb.2). Über das dynamische Gleichgewicht zwischen Gezeiten-, Gravitations- und Zentrifugal-Kräften ist somit alles gesagt. Die das Gesagte unterstützenden beiden Abbildungen, die sich nur in der Beschriftung der roten Pfeile unterscheiden, sind für erleichterten Vergleich in Abb.4 nebeneinander montiert. Noch folgende Gleichungen können als Beigabe angesehen werden. 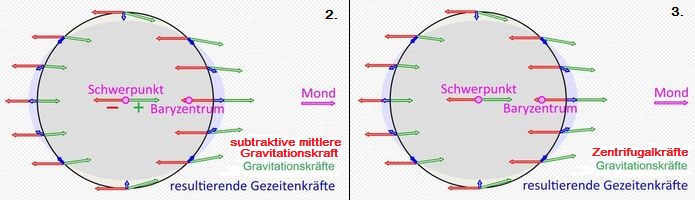 Abb.4 Abb.2 und Abb.3 (rechts) sind nebeneinander montiert.
Abb.4 Abb.2 und Abb.3 (rechts) sind nebeneinander montiert.Beigabe: Subtraktion von Gezeitenbeschleunigungen ( s. Abschnitt 2.3): ΔaG = a{r0±R} − a{r0} Die entsprechensde Gleichung für die Gezeitenkraft (anstatt für die Gezeitenbeschleunigung) lautet : ΔFG = FG{r0±R} − FG{r0} Die Fliehkraft FF ist auf der umgewälzten Erde überall gleich groß, der mittleren Gravitationskraft FG{r0} (Radialkraft) betragsgleich und in entgegengesetzte Richtung wirkend (Anmerkung 7). Die Subtraktions-Gleichung ändert sich damit zur folgenden Additions-Gleichung: ΔFG = FG{r0±R} + FF In dieser Schreibweise gilt die Gleichung nur für die beiden mittleren Randpunkte der Erde (größte Mondnähe bzw. -ferne). Sie lässt sich ohne Weiteres allgemein als für jeden beliebigen Oberflächenpunkt gültige Vektorgleichung formulieren. In der Abb.3, rechts ist diese Allgemeingültigkeit für eine größere Zahl von Oberflächenpunkten in Form von Vektoradditionen graphisch dargestellt. Zugabe: Das Gesagte möchte ich lediglich noch etwas dicker unterstreichen. Dazu gehört der Feststellung, dass keinerlei weitere rechnerische Arbeit erforderlich ist. Die wenigen einschlägigen Bemerkungen können aber Lesern dienen, die noch etwas Rechenübung, z.B. in Form von Kontrollrechnungen anstellen möchten. So lassen sich z.B. aus den Vorgabewerten der bisher verwendeten Größen die Werte für die Masse der Erde und die Periode des synodischen Mondumlaufs von reichlich 27 Tagen errechnen. Weil mit dem dynamischen Gleichgewicht lediglich eine andere Darstellung des Gezeiten-Phänomens erfolgt, müssen keine weiteren als die bisher verwendeten Primär-Zusammenhänge bekannt sein: FG = G · m1 · m2 / r02 bzw. FG = G · E · M / r02 (mit den Massen E und M von Erde und Mond) FR = m · r · ω2 bzw. FF = − E · rE · ω2 (Fliehkraft= FF = − FR =Radialkraft; mit Radius rE der Erd-Revolution) Es werden auch keine weiteren Vorgabe-Werte gebraucht als bisher: Die Erdmasse E ergibt sich aus der des Mondes mit Hilfe der den meisten Lesern bekannten Verhältniszahl E/M= 81,2 . Aus E/M = rM / rE und r0 lässt sich beispielsweise rE errechnen. Aus den Primär-Zusammenhängen lässt sich die Gleichung ω2 = G·M / (r02·rE) ableiten und damit die Winkelgeschwindigkeit ω, mit der sich Erde und Mond gegenseitig umrunden, und daraus die Länge des siderischen Mond-Monats (etwa 27,3 Tage) berechnen. 2.6 Werte der von der Sonne verursachten Gezeitenbeschleunigung auf der Erde ↑ AnfangEs gilt die unter 2.3 abgeleiteten Gleichung ebenfalls:ΔaG ≈ ∓ 2·R·G·S / r03 bzw. (Mondmasse M ist durch Sonnenmasse S ersetzt; r0 ist hier der Abstand Erde − Sonne) M = 1,989·1030 kg, Masse der Sonne, r0 = 1,496·1011 m, mittlere Entfernung der Erde von der Sonne. Mit den Werten für R, G, S und r0 ergeben sich für die Gezeitenbeschleunigung an den Erdrändern die Werte ΔaG ≈ ∓ 0,505·10−6 m/s2 (Gravitationsbeschleunigung im Erdmittelpunkt: aG0 = G·S / r02 = 5,93·10-3 m/s2) Vergleiche: Die von der Sonne verursachte Gezeitenbeschleunigung beträgt trotz der viel größeren Sonnenmasse nur etwa 46% der vom Mond verursachten. Wenn Sonne und Mond mit der Erde auf einer Linie stehen (Voll- bzw. Neumond) addieren sich beide Wirkungen: Die Springtiden sind etwa 1,5 mal so stark wie in den Zeiten dazwischen (Halbmond). Die Gravitationsbeschleunigung durch die Sonne ist zwar sehr groß (aG=5,93·10-3 gegenüber =3,32·10−5 m/s2). Die Gezeitenbeschleunigung skaliert aber mit 1/r03 (r0 in dritter Potenz), weshalb sie mit wachsendem r0 stärker abfällt als die Gravitationsbeschleunigung, die mit 1/r02 (r0 in zweiter Potenz) skaliert. Zudem ist der Erdradius R relativ zum Sonnenabstand wesentlich kleiner als relativ zum Mondabstand. Zugabe: Aus den Primär-Zusammenhängen ergibt sich die Gleichung ω2 = G·S / (r02·rE) ≈ G·S / r03 für die Winkelgeschwindigkeit ω, mit der die Erde die Sonne umrundet. Aus ihr lässt sich die Länge des Jahrs berechnen. (Die Näherung ≈ ergibt sich aus der Tatsache, dass r0 und rE praktisch gleich groß sind, das Barryzentrum Sonne/Erde fast in den Sonnenmittelpunkt fällt.) 3. Anmerkungen ↑ Anfang
Anmerkung 1
Anmerkung 2
Anmerkung 3
Anmerkung 4
Anmerkung 5
Anmerkung 6
Anmerkung 7 |
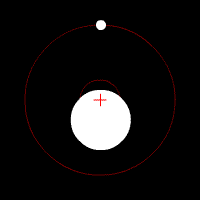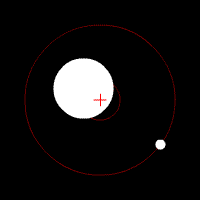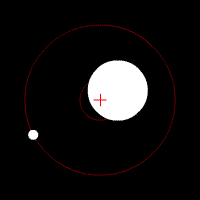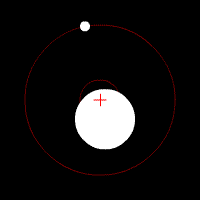 ←
Abb.1 Zwei Himmelskörper umrunden sich gegenseitig
←
Abb.1 Zwei Himmelskörper umrunden sich gegenseitig 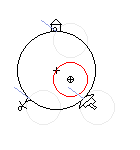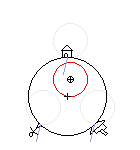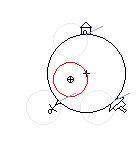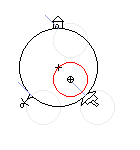
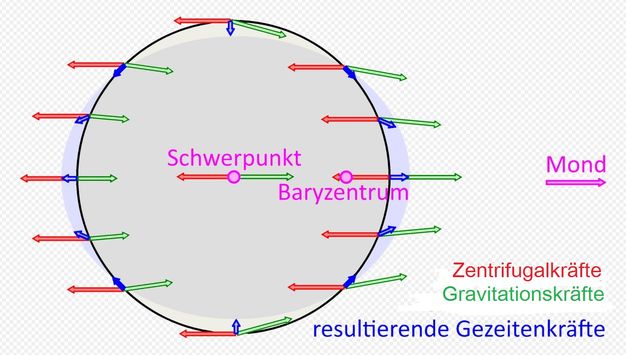 Abb.3 links: Revolution (Umwälzbewegung ohne Rotation) der Erde; von außerhalb der Erde beobachtet;
Abb.3 links: Revolution (Umwälzbewegung ohne Rotation) der Erde; von außerhalb der Erde beobachtet;