<< Home Einiges über Finsternisseabgedruckt in Chronométrophilia, No 67, Sommer 2010ZusammenfassungNach jedem sechsten, manchmal sogar schon nach einem fünften Voll/Neu-Mond gibt es wieder eine Mond/Sonnenfinsternis. Warum müssen wir trotzdem viel länger warten, um ein solches Ereignis erneut sehen zu können?Inhalt1. Einleitung2. Grundsätzliches und Begriffe 3. Das Finsternis-Limit 4. Zyklus-Bildung bei Sonnenfinsternissen 5. Der Saros-Zyklus 6. Totale Sonnenfinsternis, Verlauf 7. Sonnenfinsternis-Tourismus ist populär 8. Literatur 9. Anmerkungen 1. Einleitung ↑ AnfangDie folgende Abhandlung fasst das Grund-Wissen über Finsternisse zusammen, das sonst nur verstreut beschriebenen ist. Zur Unterstützung des Vorhabens werden vorteilhaft zeichnerische Darstellungen der Zusammenhänge verwendet. Finsternisse wiederholen sich mit einer gewissen Regelmässigkeit, was vom Saros-Zyklus, der eine Periode von ca.18 Jahren hat, allgemein bekannt ist. Es gibt auch Zyklen mit kürzerer Periode, die aber selten erwähnt werden. Der kürzeste heisst Semester-Zyklus [1] und wird hier zusätzlich besprochen, weil er wegen seiner kurzen Periode von nur 177 Tagen leicht zu erleben ist. Von den quantitativen Zusammenhängen ist vor allem das Finsternis-Limit wichtig.
2. Grundsätzliches und Begriffe ↑ AnfangEine Finsternis findet bekanntlich statt, wenn sich Mond, Erde und Sonne mit ihren Zentren ziemlich genau auf einer gemeinsamen Linie (Finsternis-Linie) befinden. Da alle drei Himmelskörper im Verhältnis zu ihren Abständen voneinander ziemlich klein sind, müssen sie diese Linie sehr genau treffen, damit sich die beiden äusseren der Drei nicht "sehen" können. Ein solcher Fall trifft nicht oft ein. In Abb.1 befindet sich die Ekliptik (Ekl) in der Zeichenebene. Die Ekliptik ist die von der Erdbahn gebildete Ebene, enthält also die Erde (E) und die Sonne (S). Die Linie zwischen ihren Zentren heisse Zentral-Linie. Die Ebene der Mondbahn (MB) ist gegen die Ekliptik ca.5° geneigt. Die Schnittpunkte der Mondbahn mit der Ekliptik sind der absteigende (auf dem Kopf stehendes Ω) und der aufsteigende (Ω) Knoten. Eine Finsternis findet nur statt, wenn sich der Mond nahe bei einem Knoten befindet. Die Verbindung der beiden Knoten -die Knotenlinie (KL)- dreht sich im All nur langsam. Es sind nur 6 (manchmal nur 5) Lunationen (Mond-Monate à ca.29,5Tage) nötig, bevor der Mond einem Knoten wieder ausreichend nahe kommt und eine Finsternis stattfindet. 6 Lunationen sind ca.177 Tage, also nur ein knappes halbes Jahr.
Von der Erde aus gesehen haben Sonne und Mond zufällig fast die gleiche scheinbare Gösse (Raumwinkel ca. 0,5°, Anmerkung 1). So muss der Neumond also genau vor die Sonne treten, damit diese total bedeckt ist (totale Sonnenfinsternis, Blick A bei 0. in Abb.1). Aber schon bei kleiner Abweichung ist die Sonnenfinsternis nur partiell (Blick B bei 6. in Abb.1). Allerdings ist die Erde doch mehr als ein Punkt: Vom Mond aus erscheint sie unter einem Winkel von ca.2,0° (Mond-Parallaxe 2·χ, Abb.2), was die Zahl der auftretenden Sonnenfinsternisse ungefähr verdreifacht. Reist man nämlich von einem mittleren Punkt O, d.h. von einem Punkt, wo die Ekliptik die Erdoberfläche schneidet, in den Hohen Norden (P) oder den Tiefen Süden, so sieht man den Mond relativ zur Sonne ca.1° tiefer oder höher stehen als vorher. Anders gesagt: Ein vorher ca.1° zu hoch bzw. zu tief stehender Mond wird jetzt in gleicher Höhe wie die Sonne gesehen.
Bei exakt gleicher scheinbarer Grösse von Sonne und Mond (μ=σ) hat dessen Kernschatten seine Kegel-Spitze auf der Erdoberfläche (Abb.3). Die Sonnenfinsternis ist punktförmig (pf, Anmerkung 2 ). Ist der Mond in seinem Erd-nächsten Punkt (Perigäum) und die Erde am weitesten von der Sonne entfernt (Aphel), so hat der Kernschatten des Mondes über 250km Durchmesser. Er läuft über die Erdoberfläche. Das schafft eine ebenso breite Zone für Totalität (tt) und bewirkt eine Finsternis-Dauer von einigen Minuten in der Zentrallinie. Beidseits dieser Zone ist die Finsternis partiell. Im umgekehrten Fall (Apogäum und Perihel) ist die Finsternis in der Zentrallinie ringförmig (rf). Die geringe Breite der zentralen Zone und die Beschränkung auf die Tageshälfte der Erde macht die Wahrscheinlichkeit einer Sonnenfinsternis an einem fixen Ort sehr klein und ist Grund für mehr und mehr "Sofi-Tourismus".
In Polnähe kann es sein, dass der Kernschatten die Erde verfehlt, dass sie nur vom Halbschatten des Mondes getroffen wird (Abb.4). In solchen Fällen spricht man auch von einer partiellen Sonnenfinsternis, bei der aber jetzt der Beobachter nicht die Möglichkeit hat, aus der partiellen in die totale Zone zu reisen. In der Astronomie gibt es den allgemeinen Begriff Bedeckung für Fälle, in denen von der Erde aus gesehen ein Himmelskörper vor einen selbst leuchtenden anderen tritt, diesen verdeckt aber nicht verfinstert. Eine Sonnenfinsternis ist ein solcher Fall. Würde man hier von einer Bedeckung sprechen, so wäre bereits auf diese Weise der Unterschied zu einer Mondfinsternis angedeutet. Bei ihr sind wir selbst (die Erde) der bedeckende Körper und verfinstern einen nicht selbst leuchtenden Himmelskörper (den Mond).
Als Mondfinsternis gilt im Allgemeinen nur derjenige Fall, in dem sich der Vollmond im Kernschatten der Erde befindet (total oder partiell, Abb.5). Mit blossem Auge ist nämlich nicht zu erkennen, wenn er nur im Halbschatten liegt. Das ist auch der Grund für die verbreitete Meinung, dass es weniger Mond- als Sonnenfinsternisse gäbe. Zählt man die Halbschatten-Ereignisse (halb) mit, unterscheiden sich die Zahlen beider Finsternisse nämlich nicht grundsätzlich. Übrigens: Vom Mond aus sieht man bei Halbschatten eine partielle Sonnenfinsternis. Schattenwerfer ist die im Vergleich zum Mond relativ grosse Erde. Ihr Kernschatten ist in der Mondgegend wesentlich grösser als der Mond selbst. Er kann den ganzen Mond bedecken. Umgekehrt: Selbst der Halbschatten des Mondes reicht bei weitem nicht aus, die gesamte Erde zu bedecken, er ist ca. 3 mal zu klein. Bei Mondfinsternissen kann sich der Beobachter die Zahl der möglichen Erlebnisse nur verdoppeln, indem er von der Tag- zur Nachthälfte der Erde reist. Ansonsten ist der Anblick des verfinsterten Mondes von überall her dergleiche. 3. Das Finsternis-Limit ↑ AnfangAbb.1 ist zur Besprechung beider Finsternis-Arten geeignet. Die im folgenden verwendeten Winkelwerte sind in ihrer Legende hergeleitet. Auf der Sonnenseite ist der Neumond (Sonnenfinsternis), aussen der Vollmond (Mondfinsternis) gezeichnet. Dargestellt sind mehrere Momente im Abstand jeweils einer Lunation. Die Mondbahn (MB) ist gegen die Ekliptik verdreht, was in den Neben-Zeichnungen A und B erkennbar ist (Verdrehwinkel 5°8'±8'). Drehachse ist die in beiden Ebenen enthaltene Knotenlinie (KL). Beim gewählten Blick auf die Ekliptik wandert die Erde dem Uhrzeiger entgegen, die Knotenlinie dreht sich ganz langsam (1 mal / 18,613 Jahre) mit dem Uhrzeiger. Ausgangssituation ist die 0. Lage. Sie ist ideal für Finsternisse. Die Monde befinden sich in den Knoten, die Knotenlinie verläuft durch den Mittelpunkt der Sonne. Die Neben-Zeichnung A ist der Blick von der Erde über den Neumond zur Sonne. Der Neumond bedeckt die Sonne, es herrscht die idealste Sonnenfinsternis. Bei der Vollmond-Variante ist es die idealste Mondfinsternis: Mond- und Kernschattenmittelpunkt übereinander. Nach sechs Lunationen ist die Situation wieder günstig für Finsternisse. Die Zentral-Linie hat sich bis auf etwa 5,36° um 180° nach links gedreht. Die Knotenlinie hat sich ausgleichend etwa 9,38° nach rechts gedreht, hat dabei aber leider überkompensiert. Der Neumond z.B. befindet sich bereits 4,023° hinter dem (jetzt aufsteigenden!) Knoten. Die Neben-Zeichnung B ist auch hier der Blick von der Erde zur Sonne (Unterseite der Ekliptik mit paralleler gepunkteter Linie angedeutet). Der Neumond hat den Knoten bereits passiert, aber er bedeckt die Sonne noch partiell. Nach 3 weiteren 177-Tage-Zyklen bzw. nach insgesamt 24 Lunationen (knapp 2 Jahre) ist die Abweichung auf 16,09° (4·4,023) angewachsen. Inzwischen ist aber schon die Situation nach der 23. Lunation besser: Abweichung nur 14,57° (29,11-16,09°+1,56). Sonnenfinsternisse finden immer noch statt, jetzt vielleicht sogar zwei im Abstand von nur einer Lunation. Wie gross die Abweichung des Mondes vom Knoten sein darf, damit noch eine Finsternis stattfindet, heisst Finsternis-Limit und soll jetzt berechnet werden (Anmerkung 3).
Ermittelt wird immer der ungünstigste Wert, d.h. gewählt wird je nach Situation entweder die kleinste oder die grösste Entfernung des Mondes und der Sonne von der Erde aus folgenden Grenzwerten: Die Neben-Zeichnung B aus Abb.1 ist in Abb.6 vergrössert und ca.180° gedreht nochmals gezeigt. Das zu betrachtende Dreieck SΩM ist ein sphärisches mit bei S annehmbarem rechtem Winkel. Der Winkel bei Ω ist die grösst-mögliche Verdrehung der Mondbahn gegen die Ekliptik (Φ=5,27°). Das gesuchte Finsternis-Limit fl ist der Bogen ΩS, als Funktion des Bogens sm zwischen Sonne und Mond. Die zur Berechnung von fl nötige Gleichung ist in der Abbildung selbst angegeben.
Wenn die Mittelpunkte von Neumond und Sonne übereinander liegen ist die Sonnenfinsternis total, besser zentral, denn in diesem Begriff ist auch die jetzt mögliche ringförmige Finsternis enthalten. Das gesuchte Limit hängt nur von der Parallaxe χmin des Mondes ab (Anmerkung 4). Die in Abb.2 angegebene Gleichung liefert bei entferntestem Mond χmin= 0,9014°. Das ist auch der sm-Wert, denn soviel darf der Mond vom Beobachter in O zu hoch gesehen werden, wenn ihn der Beobachter in P in zentraler Lage mit der Sonne sieht. Die weitere Rechnung ergibt für fl, d.h. für das Mindest-Limit ca.9,8°. Wenn sich Neumond und Sonne mehr als berühren, ist die Sonnenfinsternis partiell. χmin ist die Summe des kleinsten scheinbaren Radius des Mondes μmin und desjenigen der Sonne σmin. Diese beiden Werte werden mit den in Abb.3 angeführten Gleichungen zu 0,2455 und 0,2622 berechnet. Jetzt ist das Mindest-Limit ca.15,5°. Dieser zulässige Kleinstwert ist immer grösser als die tatsächlichen Werte nach 6 oder 5 Lunationen. Somit findet auf der Erde regelmässig nach 177 oder 147,5 Tagen eine mindestens partielle Sonnenfinsternis statt (Anmerkung 5). Bei einer Mondfinsternis ist vor allem der Durchmesser des Erd-Schattens zu beachten. In den Abb.6 entsprechenden Abbildungen 7a bis 7c ist die Sonne durch den Erd-Schatten ersetzt.
Die Mondfinsternis ist total, wenn der Mond innerhalb des Kernschattens (K) liegt. Für das Mindest-Limit interessiert der kleinste Schatten-Radius rkmin=4.461km (αmin=0,6303°). Er kommt bei nächster Sonne und entferntestem Mond zustande. Mit den Gleichungen in den Abbildungen 3, 5 und 7a ergeben sich als Mindest-Limit ca.4,2° (km = αmin - μmin).
Die Finsternis wird partiell, wenn der Mond den Kernschatten von aussen berührt (Abb.7b). Für diesen Moment ist das errechnete Mindest-Limit ca.9,6° (km = αmin + μmin), also zu klein dafür, dass jede mindestens partielle Sonnenfinsternis auch von einer mindestens partiellen Mondfinsternis begleitet ist. Die beiden Mindest-Limite 15,5° und 9,6° bilden zueinander das Verhältnis von ca. 1,6 : 1, das auch oft als Häufigkeits-Verhältnis zwischen Sonnen- und Mondfinsternissen in der Literatur zu finden ist [3].
Obwohl die Halbschatten-Mondfinsternisse mit blossem Auge niemals zu erkennen sind, wird formal doch das dafür geltende Mindest-Limit bestimmt. Dafür zählt der kleinste Halb-Schattens (H), der sich bei entferntester Sonne einstellt: rhmin=8.236 km (βmin=1,1636°). Der Mond hat wieder seine grösste Entfernung und tritt beim Mindest-Limit von ca.15,5° in den Halbschatten (Abbildungen 5 und 7c, hm= βmin+ μmin). Das ist die gleiche Bedingung wie für die Existenz einer partiellen Sonnenfinsternis. Würde man die Halbschatten-Ereignisse mitzählen, so wären die Mondfinsternisse gleich häufig wie die Sonnenfinsternisse.
4. Zyklus-Bildung bei Sonnenfinsternissen ↑ AnfangAbbildung 8 enthält graphische Lösungen sowohl für die Bildung des Semester-Zyklus als auch für die Ermittlung der Limiten. Die Ausgangsgrößen sind Mittelwerte (in der Abbildung angegeben). Innerhalb der Limiten folgen sich Finsternisse mit Semester-Periode (entsprechende Knotendistanz-Änderung=4,023°). Ausgegangen ist von einer idealen Finsternis (0. in Abb.1), die genau im absteigenden Knoten stattfindet. Die nächste Finsternis (+1) findet nach Passage der Sonne durch den aufsteigenden Knoten statt. Weiter mit Knotenwechsel folgen die Finsternisse +2 und +3. Die vierte Finsternis ist +5, denn eine Lunation vorher kommt es bereits auf der anderen Seite des absteigenden Knotens zu einer partiellen Sonnen-finsternis (+4). Der gezeichnete Semester-Zyklus begann mit der Finsternis -4 und endet mit +5 (Summe = 9 Finsternisse). Der nächste Semester-Zyklus beginnt mit der Finsternis +4 und führt über +6 bis +12 (Summe = 8). Eine Überlappung mit dem dritten Zyklus findet nicht statt. Semester-Zyklen mit 8 oder 9 Sonnenfinsternissen folgen sich unregelmäßig. Unregelmäßig ist auch, dass sie sich überlappen. Die ideale Ausgangsfinsternis ist auf der Erde vom Punkt O (Abb.2) aus zu sehen. +1 ist etwas nördlicher als zentrale Finsternis zu sehen. Bei +3 ist das Limit für zentrale Finsternisse überschritten. Befindet sich der Beobachter bereits am äußersten Punkt P (Abb.2) in der Arktis, so sieht er dennoch nur eine partielle Finsternis. Dort ist auch +5 partiell, und eine Semester-Periode später findet keine Finsternis mehr statt. Die Schnittpunkte zwischen den Mondbahnen und einer Parallele zur Ekliptik im Abstand der Parallaxe des Mondes bezeichnet das Limit für zentrale Finsternisse. Um das Limit für partielle Finsternisse zu finden, hat man diesen Abstand um die scheinbaren Radien von Sonne und Mond zu vergrößern.
Abbildung 9 enthält einen Okton-Zyklus. Bei ihm ist im Schnitt nur knapp jede achte Finsternis berücksichtigt (Die Periodendauer beträgt 47 anstatt bisher 6 Lunationen). Die Knotendistanz-Änderung ist nur noch 1,514°. Entsprechend größer ist die Zahl der Finsternisse. Der gezeichnete Zyklus enthält total 23 Finsternisse: je 11 beidseits des Knotens plus 1 im Knoten. 15 Finsternisse sind zentral, 8 sind partiell. Alle Finsternisse finden in der Nähe des aufsteigenden Knotens statt, die ersten (partiellen) in der Antarktis, die letzten in der Arktis. Mit der fast achtfachen Perioden-Dauer und der ebenfalls größeren Zahl von Finsternissen ist die Dauer eines Okton-Zyklus etwa das zwanzigfache eines Semesters. Zyklen sind Zusammenstellungen ausgewählter Finsternisse. Ihre Kenngröße ist ihre Periode, ihr Merkmal die Ähnlichkeit sich folgender Finsternisse, die umso größer, je kleiner die Knotendistanz-Änderung ist. Letztere ist umso kleiner, je besser folgende Gleichung erfüllt ist:
x·s = y·d Semester: 6s 6,5d (+4,023°) Hepton: 41s 44,5d (-2,509°) Okton: 47s 51,0d (+1,514°) Anonymos: 88s 95,5d (-0,977°) Tritos: 135s 146,5d (+0,518°) Saros: 223s 242,0d (-0,477°) Inex: 358s 388,5d (+0,041°)
In Klammern ist die Knotendistanz-Änderung angegeben. Bei + (plus) befindet sich die folgende Finsternis östlicher, 5. Der Saros-Zyklus ↑ AnfangDer Saros-Zyklus für fast identische Sonnenfinsternisse nach je 18 Jahren und 11 1/3 Tagen (18.03 Jahre) war schon den Chaldäern bekannt. Wir sind heute voller Bewunderung darüber, dass sie (wie ihre frühen Nachfolger auch) durch einfachste Beobachtungen, "mit Jahrhunderte langem astronomischen Kopfweh so viel (hier über Finsternisse) enträtselt haben" [2]. Meistens muss man sehr lange warten, bis Zeitspannen verschiedener astronomischer Vorgänge in einem gemeinsamen Vielfachen zu finden sind. Das erstaunliche ist, dass beim Saros nicht nur in einer relativ kleinen Zeitspanne (fast) ganzzahlige Vielfache von zwei Vorgängen enthalten sind, sondern sogar ein dritter hinzukommt.
Die ersten beiden Klein-Perioden sind die Lunation (synodischer Monat: 29,5306 Tage) und das aufeinanderfolgende Passieren des gleichen Mond-Knotens (drakonitischer Monat: 27,2122 Tage). Es gelten folgende Multiplikationen: Nach der 223. Lunation besteht fast wieder die ideale Situation wie am Anfang (0.). Die Abweichung zwischen Knoten und Neumond beträgt nur ca.0,477°.
Hinzu kommt drittens, dass der Mond nach dieser Zeit auch wieder fast dieselbe Position auf seiner elliptischen Bahn bzw. fast wieder die gleiche scheinbare Grösse hat. Die Bahn dreht sich nämlich ebenfalls langsam im Raum. Der Mond ist deshalb z.B. schon nach 27,5546 Tagen wieder im Apogäum (anomalistischer Monat). Multiplikation: Sogar die scheinbare Grösse der Sonne ist nicht sehr viel anders, denn die Erde ist fast auf demselben Platz ihrer Bahn um die Sonne (Differenz nur ca.11 Tage). Im Zyklus des Saros folgen sich also fast identische Sonnenfinsternisse. Eine nach 3 mal 18,03 Jahren folgende Finsternis findet sogar fast am gleichen Ort statt (dazwischen jeweils um ca.120 Längengrade verschoben). In der Zwischenzeit von 18,03 Jahren gibt es bis 40 andere Finsternisse, wovon jede einem anderen Saros-Zyklus angehört (jeder Zyklus trägt eine Nummer). Ein Saros "lebt" aber nicht ewig, er beginnt mit einer partiellen Finsternis, in der Mitte handelt es sich um totale, zum Schluss sind es wieder nur partielle Finsternisse. Zu einem Zyklus gehören ca.73 Finsternisse, woraus sich seine Lebensdauer zu 18,03·73 gleich ca.1.316 Jahre ergibt. 6. Der Verlauf einer totalen Sonnenfinsternis ↑ AnfangBei einer Sonnenfinsternis bewegt sich der Schatten des Mondes grob gesagt von West nach Ost. Die tägliche Bewegung von Sonne und Mond verläuft umgekehrt und spiegelt die Drehung der Erde um sich selbst. Also hat die Fahrt einer Finsternis eine andere Ursache: es ist die Rundfahrt des Mondes um die Erde. Die scheinbare Jahres-Bewegung der Sonne um die Erde hat zwar die gleiche Richtung, ist aber ca.12 mal langsamer (ein Jahr hat etwas mehr als 12 Lunationen). Der Mond überholt die Sonne. Sein Schatten würde mit ca.3.400km/h über die (nicht drehende) Erde rasen (Anmerkung 6). Hier hilft nun die nach Osten gehende Eigendrehung der Erde, die auf dem Äquator mit knapp 1700km/h (40.000km/24h) maximal ist.
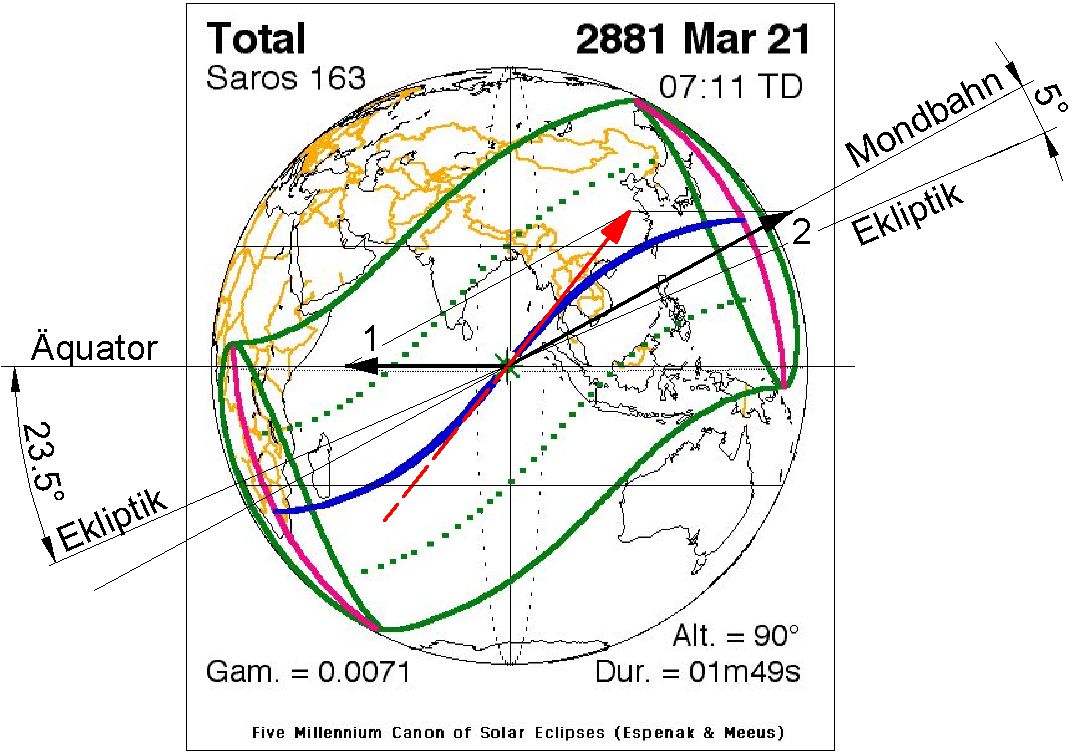
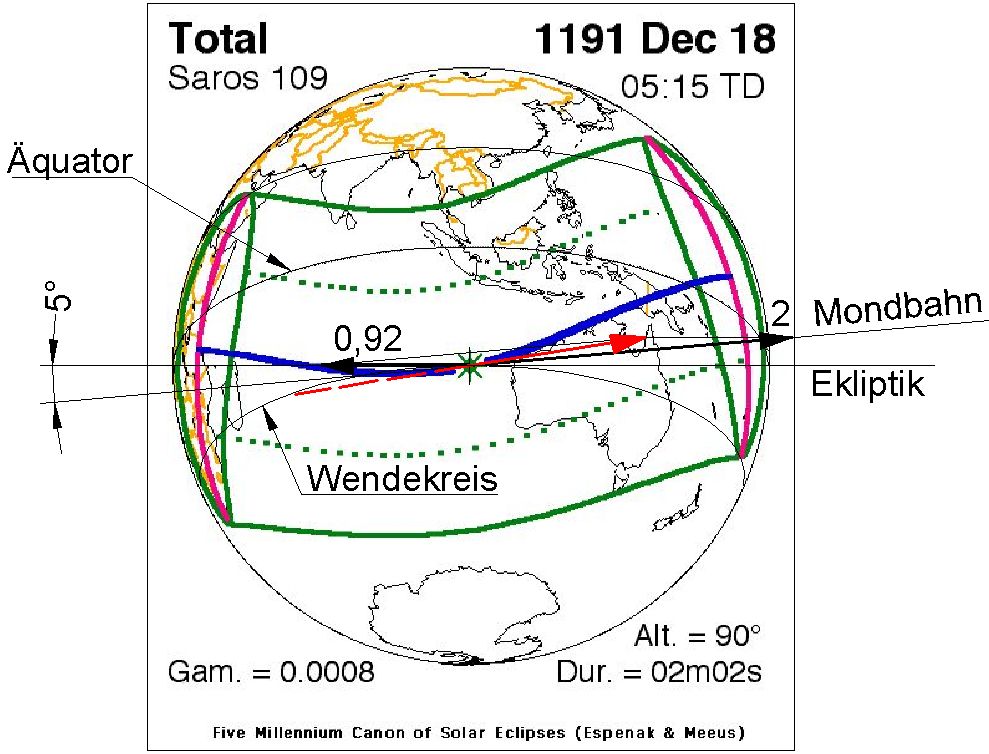
Ort der größten Totalität und Subsolarer Punkt sind identisch. Sie befinden sich in der Mitte des Bildes der Erdkugel. Die Achse des Mondschattens ist dort senkrecht zum Horizont, im Bild senkrecht zur Zeichenebene. Die Geschwindigkeitsvektoren lassen sich unverzerrt einzeichnen und addieren. Die ausgewählten Finsternisse finden zudem zu besonderen Jahresdaten statt: einmal zur Frühlings-Tag-Nacht-Gleiche, einmal zur Wintersonnenwende. An diesen Tagen ist die Lage der Ekliptik relativ zum Erd-Äquator leicht angebbar. Abbildung 10 enthält eine Finsternis zur Tag-Nacht-Gleiche. Die Ekliptik schneidet den Äquator mit dem Ekliptik-Winkel ε=23,5°. Sie wird selbst von der Mondbahn unter ca.5° geschnitten. Als Größe der Schattengeschwindigkeit ist das Doppelte der Erdgeschwindigkeit angenommen. Von ihr ist der einfache Teil abzuziehen, der infolge der Erddrehung nach Westen zeigt. Die resultierende Geschwindigkeit ist etwa 1,22 und weicht mehr als 50° von der Ostrichtung ab. Bei einer Sonnenwende (Abb.11) sind Äquator und Ekliptik momentan parallel. Die Erdgeschwindigkeit ist auf einem Wendekreis kleiner als am Äquator: ca.0,92 (=cosε). Die Resultierende ist etwa 1,09 und weicht etwa 10° von der Ostrichtung ab. In beiden Bildern stimmt die Richtung der Resultierenden (roter Pfeil) gut mit der von der NASA angegebenen Richtung (blaue Linie) der Schattenbahn am Ort der maximalen Finsternis überein. Die dennoch hohe resultierende Geschwindigkeit ist Ursache dafür, dass eine totale Sonnenfinsternis in sehr kurzer Zeit über einen Ort hinweg geht. Als grösst-möglicher Kernschatten-Durchmesser werden 264km [3] und als längste mögliche Zeit für eine in Äquator-Nähe stattfindende totale Sonnenfinsternis 7,67min [2] angegeben. Es handelt sich dabei also nicht um einen der untersuchten Sonderfälle und auch nicht um nur einen Fall, in dem beide Extremwerte gleichzeitig auftreten würden. 7. Sonnenfinsternis-Tourismus ist populär ↑ Anfang
Die folgende abschliessende Bemerkung ist die Übersetzung eines Zitats [2]: 8. Literatur ↑ Anfang
[1] G. Van den Bergh: "Periodicity and Varation of Solar (and Lunar) Eclipses", Haarlem 1955 9. Anmerkungen ↑ Anfang
Anmerkung 1 ↑ zurück
Anmerkung 2 ↑ zurück
Anmerkung 3 ↑ zurück
Anmerkung 4 ↑ zurück
Anmerkung 5 ↑ zurück
Anmerkung 6 ↑ zurück
Anmerkung 7 ↑ zurück
Siegfried Wetzel, CH 3400 Burgdorf, Mai 2008/Nov.08/Nov.09/Nov.11
|
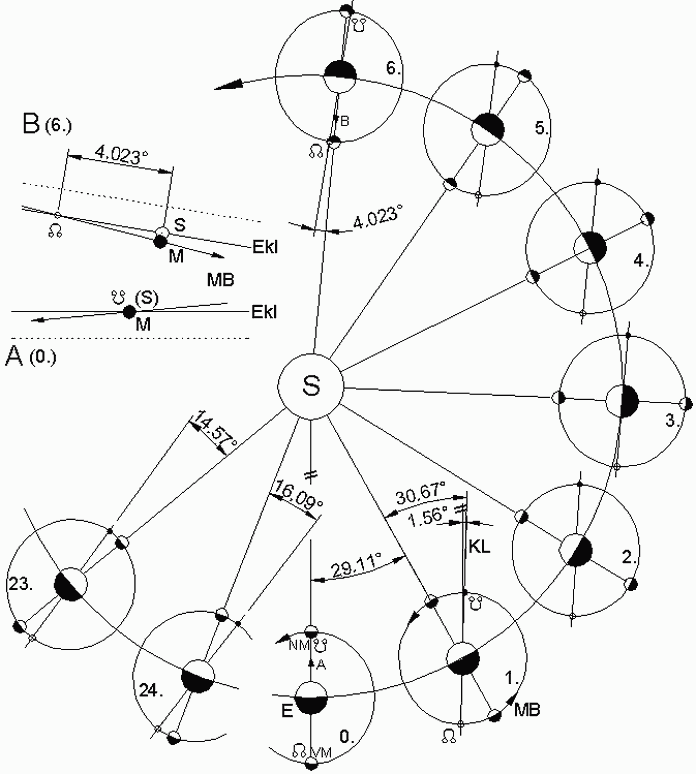Abb.1 Erde und Mond auf ihrer Bahn um die Sonne nach jeweils einer Lunation
Abb.2 Mond-Parallaxe (Winkel-Gösse der Erde vom Mond aus gesehen)
Abb.3 der Kern-Schatten des Mondes auf der Erd-Oberfläche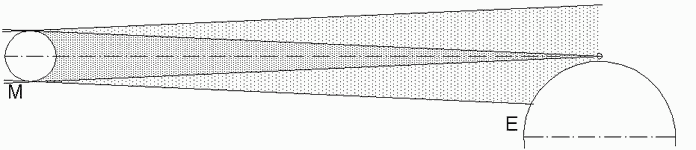
Abb.4 der Kern-Schatten des Mondes verfehlt die Erde
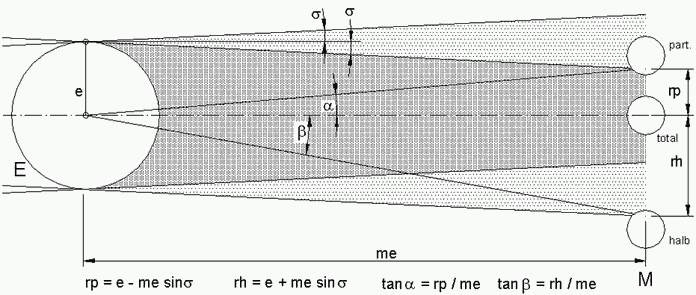Abb.5 der Mond im Kern- und Halbschatten der Erde
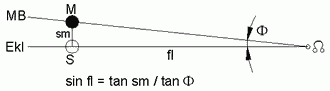<< Abb.6 Sonnenfinsternis-Limit fl
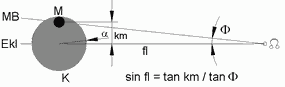<< Abb.7a totale Mondfinsternis
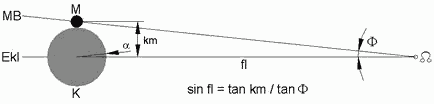<< Abb.7b partielle Mondfinsternis
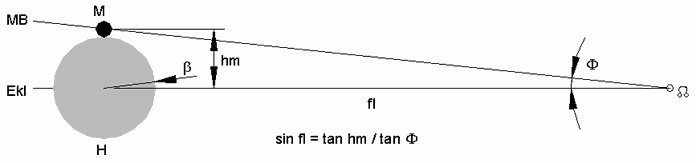Abb.7c Halbschatten-Mondfinsternis
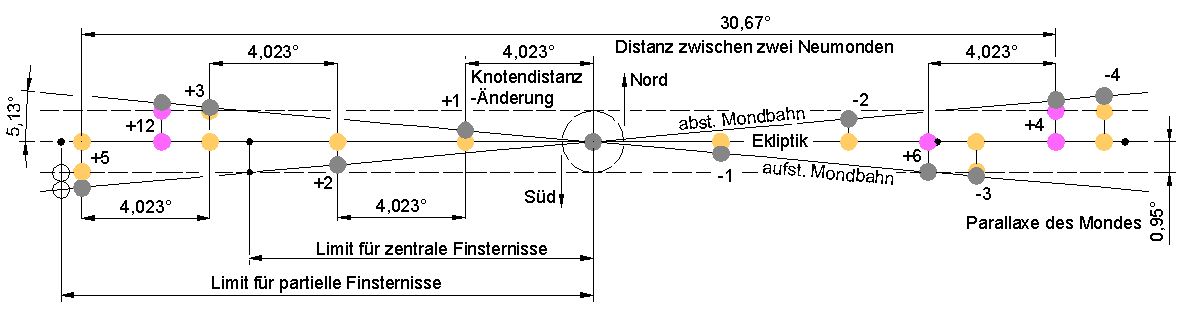Abb.8 Sonnenfinsternis, Semester-Zyklus
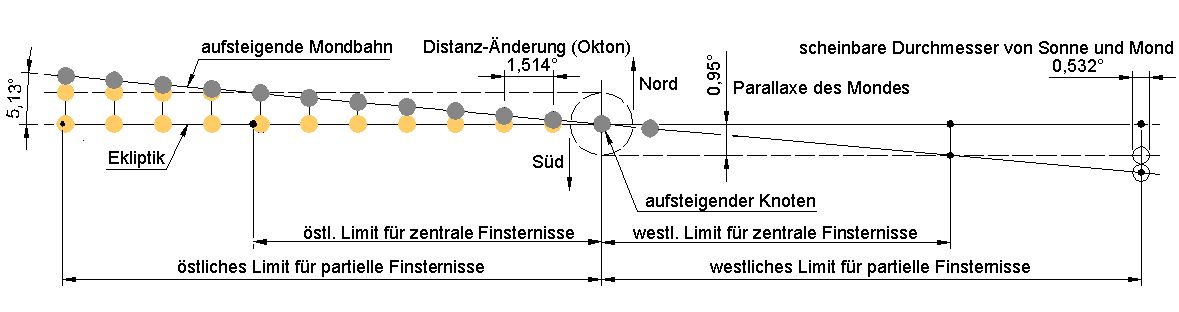Abb.9 Sonnenfinsternis, Okton-Zyklus
