<< Home
<< andere Sonnenuhren-Beiträge
↓↓ Ende
Sonnenuhr und Mathematik
(DGC-Jahresschrift 1999)
Zusammenfassung
Die Sonnenuhr ist ein gut geeignetes, zeitloses Objekt für mathematische Uebungen. Andererseits eignet sich Mathematik vorzüglich als klare Sprache für die zu Herstellung und Gebrauch nötige Erklärung der Sonnenuhr. Es ist wahrscheinlich, dass bei der Abstraktion von den Gegenständen zur reinen Mathematik -im engeren Sinne zur analytischen Geometrie- auch vom Gegenstand Sonnenuhr ausgegangen worden ist. Die nutzbringende Verwertung der reinen Mathematik beschert uns gelegentlich wieder eine neuartige Sonnenuhr.Einleitung
In einer früheren Arbeit [1] stellte ich fest, dass es seit dem Beginn der Neuzeitlichen Wissenschaft überwiegend mathematisch dominierte Literatur über Sonnenuhren gibt, und dass diese häufig als Berichte zu mathematischen Uebungen angesehen werden müssen. Nachdem ich mich in der o.g. Arbeit auf die physikalische Betrachtungsweise der Sonnenuhr beschränkte, möchte ich jetzt der Rolle der Mathematik für unseren Gegenstand nachgehen. Meine Betrachtungsweise ist die eines Ingenieurs, d.h. eines am realen Gegenstand Sonnenuhr Interessierten. Ich werde mich aber bemühen, das Thema nicht berufsspezifisch sondern allgemein zu behandeln.Inhalt
1. Mathematische Aspekte bei Sonnenuhren2. Die Polstab-Sonnenuhr und ihre Grundgleichung
3."Die eigenartigen Sonnenuhren des Jaques Ozanam" [2]
4. Die gnomonische und die Bifilar-Sonnenuhr [3]
5. Literatur
1. Mathematische Aspekte bei Sonnenuhren ↑ Anfang
Die Eigendrehung der Erde, die Relativ-Bewegung zwischen Erde und Sonne und die Entstehung eines Schattens im Sonnenlicht sind Naturerscheinungen, die wir der naturwissenschaftlichen Disziplin Physik zuordnen [1]. Im Wesentlichen sind es diese Beziehungen, die bei der Sonnenuhr eine Rolle spielen.
Das Verhältnis zwischen Sonnenuhr und Mathematik werde ich unter vier von mir gewählten Aspekten diskutieren:
Erster Aspekt: Abstraktion
Aufgabe der Mathematik ist es, ausgehend von gegenständlichen Erscheinungen abstrakte Beziehungsgefüge zu finden, die letztlich der Gegenstände nicht mehr bedürfen. Das Ergebnis einer solchen Abstraktion ist die analytische Geometrie, die von Descartes im 17.Jahrhundert begründet wurde. Es ist wahrscheinlich, dass diese Abstraktion auch vom Gegenstand Sonnenuhr ausgegangen ist, denn viele Schriften über Sonnenuhren stammen von Mathematikern, die Zeitgenossen von Descartes waren. Als Beispiel wähle ich Ozanam, der uns eine grössere Zahl "eigenartiger Sonnenuhren" [2] hinterliess. Sein allgemeiner Gedanke zu dieser Vielzahl von - im engeren Sinne - Sonnenuhren-Zifferblättern bleibt unerwähnt. Ich werde eine allgemeine Aussage machen.
Zweiter Aspekt: Nutzbringende Verwertung
Die analytische Geometrie zählt zur reinen Mathematik. Als angewandte Mathematik gilt u.a. die nutzbringende Verwertung der reinen Mathematik. Dafür nenne ich Michnik [3], der ausgehend von der inzwischen hochentwickelten analytischen Geometrie am Anfang des 20.Jahrhunderts die Bifilar-Sonnenuhr erdachte.
Dritter Aspekt: Mathematik als Sprache
Schliesslich und vor allem wende ich allgemeine mathematische Schulkenntnisse als kurze und klare Sprache zusätzlich immer dann an, wenn die Umgangssprache versagt, wenn die mathematische Formulierung der Zusammenhänge für alle - nicht nur für Ingenieure - am hilfreichsten ist. In diesem Sinne beschreibe ich zuerst die Polstab-Sonnenuhr mit Hilfe einer Grundgleichung, bevor ich mich Ozanam und Michnik zuwende und dabei ebenfalls mathematische Formulierungen gebrauche.
Vierter Aspekt: Mathematisches Uebungsobjekt
Dass sich die Sonnenuhr vorzüglich als Objekt beim Einüben von Mathematik eignet, ist die einleitend genannte allgemeine Feststellung. Die Herleitung der o.g. Grundgleichung, die Beschäftigung mit Ozanam's und Mischnik's Arbeiten und die beiden Arbeiten selbst sind Beispiele dafür.
2. Die Polstab-Sonnenuhr und ihre Grundgleichung ↑ Anfang
Der Ort der Sonne am Himmel lässt sich z.B. mit räumlichen Polar-Koordinaten angeben. In das Foto einer Gartenplastik (Abb.1), die ich mir als prinzipielle Darstellungshilfe für die scheinbaren Bewegungen der Sonne schuf [1], habe ich diese Koordinaten eingetragen.
Der Abstand von der Sonne ist mit der Zeit fast unveränderlich und hat keinen merklichen Einfluss auf das Erd-Geschehen. Die Aenderung der Deklination erleben wir als Wechsel der Jahreszeiten, und dem Stundenwinkel entspricht die Tageszeit. Dass der Stundenwinkel in diesem Koordinatensystem direkt erscheint, ist ein Grund dafür, es - insbesondere für Sonnenuhren - bevorzugt zu verwenden.
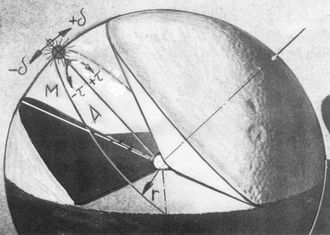
<< Abb.1 Gartenplastik "Sonnensektor" [1]
mit Sonne und Polar-Koordinaten
A=Aequator-Ebene, M=Meridian-Ebene,
r=Abstand Erde-Sonne, δ=Deklinationswinkel,
τ=Stundenwinkel
An den Tag/Nacht - Gleichen gewinnen wir eine Koordinatenfläche, die sich, weil sie eben ist, als Bezugsfläche für die Deklination vorzüglich eignet. Für sie gilt: δ= 0. In ihr liegen auch der Erd- und der Himmelsäquator (Aequator-Koordinatensystem [5]).
Der Stundenwinkel ist auf ihr ablesbar. Als Bezugsfläche für ihn wird die örtliche Meridian-Ebene (Ortsäquator-Koordinatensystem [5]) verwendet. Also gilt τ = 0, wenn die Sonne am höchsten über dem Horizont steht, wenn wahrer Mittag ist:
 Abb.2 Aequatoriale Sonnenuhr (Modell einer Brunnen-Plastik)
Abb.2 Aequatoriale Sonnenuhr (Modell einer Brunnen-Plastik)
Bei der äquatorialen Sonnenuhr (Abb.2) liegt das Zifferblatt in der o.g. genannten Aequatorfläche, weshalb diese Sonnenuhr leicht zu verstehen ist. Der Schatten zur Kennzeichnung des Stundenwinkels stammt von einem Polstab, der sowohl durch den Pol des Koordinatensystems führt als auch zum Himmelspol zeigt. Seine Lage und die Analogie seiner Schattenbildung zur Abbildung mit einer Zylinderlinse [1] sind Voraussetzung und Erklärung dafür, dass der Schatten tatsächlich den Stundenwinkel und nicht ?wie im allgemeinen Falle? eine Grösse repräsentiert, die auch von der Deklination bestimmt ist. Wegen der besonderen Lage des Zifferblattes folgt der Stabschatten dem Stundenwinkel winkeltreu.
Die äquatoriale Sonnenuhr ermöglicht uns nun die einfache Herleitung einer in der Gnomonik häufig gebrauchten Grundgleichung, mit deren Hilfe jedes ebene Zifferblatt einer Polstab-Sonnenuhr skaliert werden kann. Beispielhaft folgt die Herleitung der entsprechenden Gleichung für das horizontale Zifferblatt. Die mathematisch-geometrische Abstraktion der prinzipiellen Zusammenhänge führt von Abb.2 zu Abb.3.
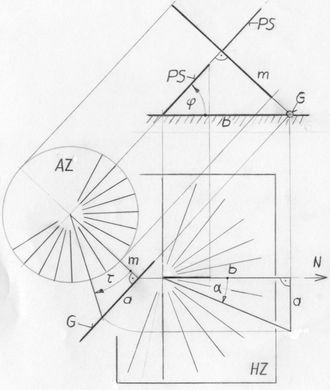
<< Abb.3 Grundgleichung für die horizontale Polstab-Sonnenuhr
PS=Polstab, AZ=äquatoriales ..., HZ=horizontales Zifferblatt
Der Stundenwinkel τ der Sonne ist identisch mit dem Skalenwinkel α' auf dem äquatorialen Zifferblatt, denn der Stabschatten folgt ihm winkeltreu: α' = τ. Die herzuleitende Gleichung beantwortet die Frage nach dem Skalen-Winkel, der durch den Stabschatten desselben Polstabes auf horizontalem Zifferblatt entsteht. Die verlängerten radialen Skalenstriche des äquatorialen Zifferblatts durchstossen das horizontale Zifferblatt in der Geraden G, auf der wir für α' = τ die Hilfslänge a gewinnen. Das horizontale Zifferblatt ist die Wasser-Fläche in Abb.2. Auf ihr könnte der Schatten, ausgehend vom Eintauch-Punkt des Polstabes, sichtbar werden, wenn der aus dem Wasser ragende Körper (mit äquatorialem Zifferblatt) entfernt würde. Bezugsrichtung ist wieder die Mittags-Sonne, d.h. der entsprechende Stabschatten.
Mit Hilfe von a und der weiteren Hilfslänge b (Mass für den Breitenwinkel φ) gewinnen wir schliesslich den Skalen-Winkel α zu
tan α = sin φ·tan τ.
Die wenigen Zwischen-Gleichungen sind die folgenden:
tan α = a / b (unten in Abb.3),
a = m·tan τ (links in Abb.3),
b = m / sin φ (oben in Abb.3).
Die beiden letzten Gleichungen sind in die erste Gleichung einzusetzen.
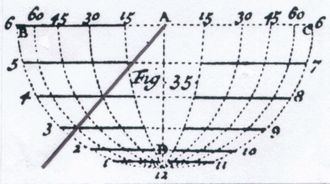
<< Abb.4 Ozanam's "elliptische Horizontaluhr"
mit zusätzlichem Stabschatten [2]
gerade Stunden-, elliptische Breiten-Linien
mögliche Anzeigen:
3 Uhr (φ≈60°), 4 Uhr (φ≈30°), 5 Uhr (φ≈15°)
3. "Die eigenartigen Sonnenuhren des
Jaques Ozanam" [2] ↑ Anfang
Unter diesem Titel berichtet Rohr über Sonnenuhren, die er in den Schriften von Ozanam gefunden hat. Es handelt sich um verschiedene "eigenartige" Zifferblätter für die horizontale Polstab-Sonnenuhr (Abb.3, unten), die aber hier für jede geografische Breite φ eingerichtet und benutzt werden kann.
Der Schattenstab ist in seinem Fusspunkt drehbar - aber in der Meridian-Ebene verbleibend -befestigt, sodass er leicht auf den Himmelspol ausrichtbar ist.
Auf den Zifferblättern (Abb.4) befinden sich nicht die vom Fusspunkt ausgehenden radialen Stundenlinien. Statt dessen gibt es Stundenlinien beliebig erscheinender Form und Lage. Der Stabschatten fällt nicht in seiner ganzen Länge auf eine solche Stundenlinie. Er kreuzt sie nur, mehrere gleichzeitig. Die Schar der Stundenlinien wird von einer weiteren Linien-Schar gekreuzt, die Breitenkreislinien genannt werden.
Für die Zeitbestimmung gilt nun diejenige Stundenlinie, durch deren Kreuzungspunkt mit dem Stabschatten auch die örtlich geltende Breitenkreislinie verläuft.
Ozanam hinterliess uns eine Menge solcher ganz verschiedener, für denselben Zweck bestimmter Zifferblätter. Rohr übernimmt nur vier dieser Zifferblätter. Aber bereits diese vier Stück stellen sofort die Frage nach der Gemeinsamkeit, die in der Verschiedenheit verborgen ist. Die Antwort ist die Abstraktion, die wir uns als bescheidenes Beispiel mathematischer Arbeit vorgenommen haben.
Zur Anzeige des Stundenwinkels bzw. der Tageszeit genügt eine einzige Koordinate. Der Schatten einer Polstab-Sonnenuhr geht immer vom Fusspunkt des Stabes aus. Dieser Punkt sei der Pol eines ebenen Polar-Koordinatensystems. Die einzig gebrauchte Koordinate ist der Winkel des ausreichend langen Schattens. Wird aber nur ein Punkt des Schattens benutzt, so ist auch die Koordinate Radius nicht mehr unbestimmt. Bei der gnomonischen Sonnenuhr (s.Abschnitt 4) ist der Schatten selbst punktförmig, sein Radius (dort aber vom Fusspunkt des Gnomons aus gemessen!) ein Mass für die Sonnenhöhe über Horizont.
Ozanam wollte ein Zifferblatt, dass für alle Breitengrade verwendbar ist. Es wäre verwirrend, wenn es für mehrere Breitengrade entworfene radiale Linien-Büschel enthielte. Also reduzierte er jede dieser radialen Linien auf je einen Punkt. Zur Unterscheidung genügt eine
einzige Bedingung: Unterschiedlicher Radius für unterschiedlichen Breitengrad.
Dann verband er diese Punkte untereinander wieder durch neue Linien: Eine Schar von Linien, auf denen die Punkte gleichen Stundenwinkels liegen, eine aus Linien, mit denen die Punkte nach dem Kriterium gleicher Breitengrad verbunden sind. Beide Scharen bilden ein Netz.
Die Auswahl der Punkte unter der o.g. einzigen Bedingung führt zu einer unbegrenzten Vielfalt möglicher Liniennetze. Das ist bereits die gesuchte verallgemeinerte Aussage.
Die von Ozanam angegebenen Zifferblätter sind Sonderfälle, nämlich solche, bei denen alle Linien des Netzes nicht beliebige, sondern die eine Kurvenschar Geraden, die andere einfache ebene Kurven sind: Geraden, Ellipsen, Parabeln und Hyperbeln, mit einem Wort: Kegelschnitte.
So gesehen lässt sich seine Arbeit auch als Uebungsbeispiel ansehen für:
analytische Geometrie - Kurven in der Ebene - Kegelschnitte.
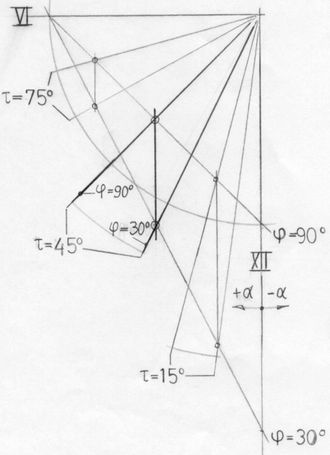
<< Abb.5 Ozanams "geradlinige Horizontaluhr" [2]
In Abb.5 wird die "geradlinige Horizontaluhr" [2] nochmals hergeleitet. Beide Linien-Scharen bestehen aus Geraden.
Ueber jedes radiale Linien-Büschel mit τ=konst. wird eine Gerade parallel zur Mittagslinie gelegt. Die Lage der Parallelen wird so gewählt, dass alle Punkte für φ=90° auf der Sehne des betreffenden Viertelkreises liegen. Alle anderen Linien φ=konst. sind dann ebenfalls Geraden. Auf den Beweis wird verzichtet. Aber: Für τ=±90° (6 Uhr) ist die Schattenrichtung von φ unabhängig (α=τ=±90°). Also schneiden sich alle Geraden φ=konst. auf der Geraden α=±90° (Ost-West-Richtung, ein Schnittpunkt für die Vormittagsstunden im Westen, einer für die Nachmittagsstunden im Osten).
Abb.5 bzw. Ozanam's Originalzeichnung gab mir auch eine Anregung für eine mechanische Lösung des Problems: Prinzipskizze in Abb.6.
Mit dem bei D (6 Uhr) drehbaren Hebel H (vorzugsweise auf der Zifferblattrückseite angebracht) lassen sich die Stundenstäbe S gemeinsam um den Fusspunkt Z des Polstabes verdrehen und stufenlos auf einen Wert φ einstellen. Die Ausführung der skizzierten Idee verlangt allerdings konstruktives Können, um die Lagerung aller Stundenstäbe und des ebenfalls drehbaren Polstabes im Punkt Z unterzubringen. Das mindestens zweigliedrige Gleitstück G bewegt sich gleichzeitig auf drei Geraden: Auf seinem Stundenstab S, auf dem Hebel H und in seiner Geradführung F auf dem Zifferblatt.
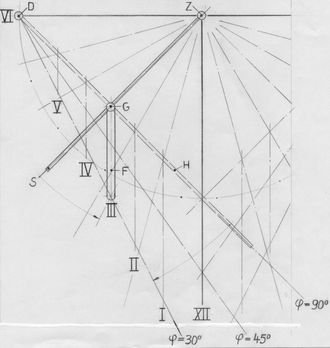
<< Abb.6 Polstab-Sonnenuhr
mit einstellbaren Stundenstäben
H=Hebel, D=Hebel-Drehpunkt, S=Stundenstab,
Z=Stab-Drehpunkt, G=Gleitstück, F=Führung
4. Die gnomonische und die
Bifilar-Sonnenuhr [3] ↑ Anfang
Bei einer gnomonischen Sonnenuhr (Abb.7) wirkt immer nur ein punktförmiger Schattenwerfer. Im einfachsten Falle ist das die Spitze G eines Stabes. Ein solcher Stab heisst Gnomon, wenn er senkrecht auf horizontalem Zifferblatt steht.
Die im Abschnitt 2 hergeleitete Grundgleichung gilt ebenfalls. Zu beachten ist allerdings, dass der gemeinsame Ursprung der Stundenlinien nicht der Fusspunkt G' des Gnomons ist. Sie entspringen dem Fusspunkt F eines denkbaren, die Gnonom-Spitze G enthaltenden Polstabes. Auf einer Stundenlinie befindet sich nur ein Schattenpunkt G'', dessen Abstand vom o.g. Ursprung zusätzlich ein Mass für den Deklinationswinkel d ist. Die örtliche Grösse Breitengradwinkel j ist als Konstante im Zifferblatt enthalten. Die Linien gleicher Deklination sind die Hyperbeln. Die Auswahl der Deklinationswerte in Abb.7 entspricht der gebräuchlichen Einteilung des Jahres in 12 gleich lange Abschnitte (Tierkreiszeichen).
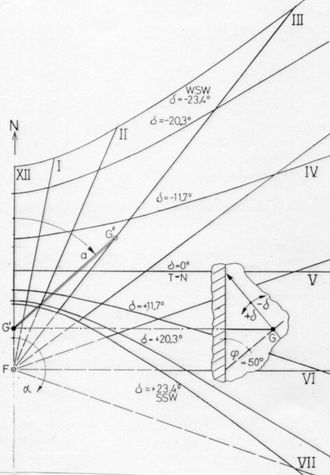
<< Abb.7 Gnomonische Sonnenuhr
G=Gnomon-Spitze, G'=Gnomon-Fusspunkt
G''=Schatten von G, F=Ursprung der Stundenlinien
Bei der Bifilar-Sonnenuhr von Michnik [3] ist der als Zeiger dienende Schatten ebenfalls ein Punkt. Es ist der Schnittpunkt zweier Linien-Schatten, die von zwei waagerechten sich rechtwinklig kreuzenden Fäden stammen. Es handelt sich deshalb um eine im Prinzip gnomonishe Sonnenuhr. Wegen der beiden Fäden anstelle eines punktförmigen Schattengebers ist die Atraktivität als mathematisches Uebungsobjekt nochmals gesteigert. Michnik's Arbeit "Die Theorie einer Bifilar-Sonnenuhr" ist folgerichtig ein ausgesprochen mathematisches Werk. Sie ist sehr allgemein gehalten und sehr interessant, beantwortet aber auch Fragen, die für Herstellung und Gebrauch einer Sonnenuhr ohne Bedeutung sind ( Beispiel: Welche Fläche bilden die Strahlen eines Tages zwischen Sonne und Anzeige-Punkt?). Es überrascht dann beinahe, dass sich schliesslich ein Sonderfall beim Höhen-Verhältnis der Fäden als Erfindung einer neuen Sonnenuhr erweist. Nachfolgend ist mit der Bezeichnung Bifilar-Sonnenuhr nur dieser Sonderfall gemeint.
Diese Sonnenuhr (Abb.8) hat eine verblüffende Eigenschaft:
Der Winkel Δα' zwischen den Stunden-Linien ist - wie bei der äquatorialen Sonnenuhr (Abb.2) - immer gleich 15°.
Michnik wirkte erst am Anfang des 20. Jahrhunderts, was zeigt, dass die im 17. Jahrhundert begründete mathematische Sonnenuhren-Tradition ungebrochen ist. Sie dauert heute noch an. Er kam mit Hilfe der inzwischen hoch entwickelten analytischen Geometrie zu seinem Entwurf. Es ist kaum vorstellbar, dass ein Nicht-Mathematiker der Erfinder sein konnte, obwohl die Erklärung dieser Sonnenuhr im nachhinein mit Schulmathematik möglich ist.

<< Abb.8 Bifilar-Sonnenuhr nach Michnik [4]
Wegen des gegenseitigen Abstandes der Fäden variiert der im gemeinsamen Punkt-Schatten wirksame Ort auf beiden Fäden über den Tag und übers Jahr (die Deklination ist grundsätzlich auch ablesbar), was die Erklärung schwierig erscheinen lässt. Sie sollte aber mit Hilfe von Abb.9 gelingen.
Wenn wir den tieferen, den Ost/West-Faden durch seinen mittleren Punkt M ersetzen, erhalten wir eine einfache gnomonische Uhr. Die Stunden-Linien schneiden sich in einem Punkt, der auch der Fusspunkt F eines durch den gnomonischen Punkt M führenden Polstabs wäre. Die Grundgleichung (s. Abschnitt 2) gibt den Winkel a dieser geraden Linien an:
tan α = sin φ · tan τ,
(φ = geografische Breite, τ = Stundenwinkel).
Mit Hilfe des oberen, des Süd/Nord-Fadens wird nun dieser gnomonischen Abbildung eine Ost/West-Verschiebung überlagert. Am Nachmittag - wie in Abb.9 - fällt das Schatten-Kreuz K' weiter östlich auf das Zifferblatt als der Schatten M' des mittleren Punktes M des unteren Fadens. Die Stunden-Linien der Richtung α' haben denselben Schnittpunkt F, nur fächern sie stärker auseinander als die mit Richtung α(rechts in Abb.9). Die Hyperbeln werden gestreckt.
Das Streckungs-Verhältnis ist α' / α = h' / h . Es folgt aus zwei ähnlichen Dreiecken, die von zwei parallelen Sonnen-Strahlen gebildet werden: Abb.9, links (Die Blickrichtung ist Süd.). Mit h' / h lässt sich das Streckungs-Verhältnis wählen.
Mit der Wahl h' / h = 1 / sin φ
(eines vom Breitengrad abhängigen Verhältnisses ! )
wird
α' = τ ,
was das Besondere der Bifilar-Sonnenhr ist.
Die Zwischenschritte sind:
1. Abb.9, rechts: tanα'/ tanα = a'/a,
2. mit a'/a = h'/h: tanα' = tanα (h'/h),
3. mit Grundgleichung: tanα' = sinφ tanτ (h'/h),
4. mit h'/h = 1/sinφ: tanα' = tanτ.
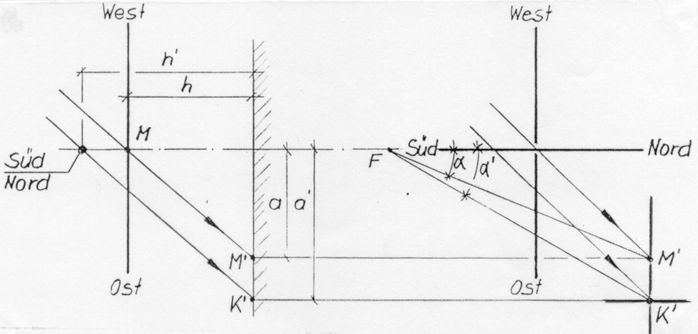 Abb.9 Erklärung der Bifilar-Sonnenuhr nach Michnik
Abb.9 Erklärung der Bifilar-Sonnenuhr nach Michnik
gezeichnet sind die Verhältnisse für die 2. Stunde nach Wahrem Mittag
Die Uhr kann horizontal oder auf jeder nach Süd gekippten Ebene, also auch auf einer "kostenlosen" Südwand, sein. Das ist ein Vorteil gegenüber der ebenfalls gleichmässig geteilten äquatorialen Polstab-Uhr. Genereller Nachteil, sogar gegenüber einer einfachen gnomonischen Uhr, sind die unscharfen Schatten am Rande bei tiefem Sonnenstand wegen der teilweisen Schattenbildung mit Hilfe des hochliegenden oberen Fadens. Die Uhr von Abb.8 ist deshalb schmal. Sie zeigt im Winter nur ±2 Stunden an, obwohl der Tag mit ca.8 Stunden noch doppelt so lang ist. Die einfache gnomonische Uhr von Abb.7 zeigt bei gleich langem Schatten im Winter immerhin ca.±2,5 Stunden an.
Meine Aussage, dass mit der Polstab-Sonnenuhr die abschliessende gnomonische Erfindung bereits am Ende des Mittelalters gemacht worden sei [1], wird auch durch Michnik's genialen Entwurf, der "nur" eine andere gnomonische Sonnenuhr ist, nicht erschüttert. Zur Untermauerung dieser allgemeinen Aussage betrachten wir nochmals Abb.7:
Das Zifferblatt einer Polstab-Uhr mit bis zur Gnomon-Spitze G reichendem Polstab würde nur ungefähr ein Viertel (Kantenlängen) so gross wie das gnomonische Zifferblatt sein. Zur Zeitablesung dient immer der vom Fusspunkt F ausgehende ganze Stabschatten. Sein Winkel kann sicher auf einem Kreisbogen um F, dessen Radius nicht grösser als die Polstablänge zu sein braucht, bestimmt werden. Das gilt von Sonnenaufgang bis -untergang, während der gnomonische Punktschatten erst viel später bzw. schon viel früher ablesbar bzw. nicht mehr ablesbar ist. Zu seiner unpraktisch grossen Entfernung kommt noch, dass er dabei auch nicht als scharfer Punkt erkennbar ist.
Resumè: Der Entwurf Michnik's ist faszinierend und wurde von keinem späteren Entwurf mehr übertroffen. Gegenüber einer einfachen gnomonischen Sonnenuhr hat die Bifilar-Uhr einen Vorteil, sie hat aber auch Nachteile. Die Polstab-Sonnenuhr bleibt ohnenhin unerreicht.
5. Literatur (inkl. Bildnachweise) ↑ Anfang
[1] S.Wetzel: "Die Physik der Sonnenuhr", SFAU 1998
[2] R.Rohr: "Die eigenartigen Sonnenuhren des Jaques Ozanam", SFAU 1985
[3] H.Michnik: "Theorie einer Bifilar-Sonnenuhr", Astronomische Nachrichten, 1923
[4] R.Rohr: "Die Sonnenuhr", München 1982
[5] H.Schilt: "Koordinatensysteme der Astronomie", ORION-Sondernummer, 1980
SFAU = Schriften der "Freunde alter Uhren"
![]() Siegfried Wetzel, CH 3400 Burgdorf, Januar 2008
Siegfried Wetzel, CH 3400 Burgdorf, Januar 2008
↑↑ Anfang
<< andere Sonnenuhren-Beiträge
Druck-Version (2-spaltig, 7 Seiten, *.pdf, 1.7mB) >>
<< Home